肖 兵

?

部分非線性回歸模型的非線性度量

肖 兵*

(湖南文理學(xué)院 數(shù)學(xué)與計算科學(xué)學(xué)院, 湖南 常德, 415000)

利用傳統(tǒng)曲率理論度量回歸模型的非線性程度, 分析其缺陷, 并對幾類實例模型進行探討, 進而提出基于局部近似的新度量方法, 在一定程度上彌補了傳統(tǒng)方法的缺陷; 還研究了模型參數(shù)基于局部線性近似的最小二乘估計的漸進性質(zhì)及其求法中迭代初值的選取和改進方向.

非線性度量; 固有曲率; 參數(shù)效應(yīng)曲率; 局部曲率

本文探討部分非線性回歸模型:

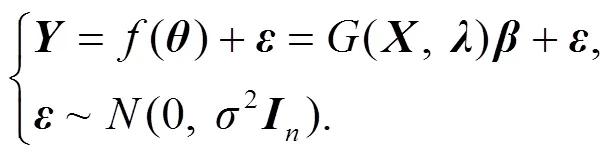
各類回歸模型中嚴格的線性模型并不多見, 在實際運用中會遇到大量的非線性參數(shù)的情形, 此處非線性是指模型函數(shù)關(guān)于未知參數(shù)的一階導(dǎo)數(shù)仍然是該未知參數(shù)的一次或一次以上函數(shù), 但關(guān)于非線性回歸模型的研究成果有限且進展緩慢. 對于非線性模型的研究通常要解決2方面的問題, 一是模型函數(shù)的求解, 目前許多文獻已基本解決此方面的問題[1—2];二是模型的非線性程度的度量, 近年來此問題還未得到比較一致的或比較滿意的結(jié)論與方法, 基本上都是利用對模型函數(shù)的線性近似估計理論及傳統(tǒng)的幾何曲率理論或偏差理論來進行探討. 本文先用固有曲率及參數(shù)效應(yīng)曲率相關(guān)理論進行研究.

1 部分非線性模型非線性度量整體曲率法

非線性回歸模型的非線性可分為2部分: 固有非線性, 取決于解軌跡的曲率; 參數(shù)效應(yīng)非線性, 基于參數(shù)線在解軌跡的切平面上的投影一般不是直線, 不互相平行, 參數(shù)線間也不是等距的, 這里參數(shù)線是指參數(shù)空間的參數(shù)直線映射到期望曲面中的曲線. 以下根據(jù)微分幾何中的曲率理論探討模型(1)的非線性度量.

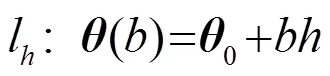
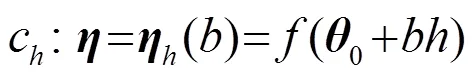
該曲線稱為提升線. 由于

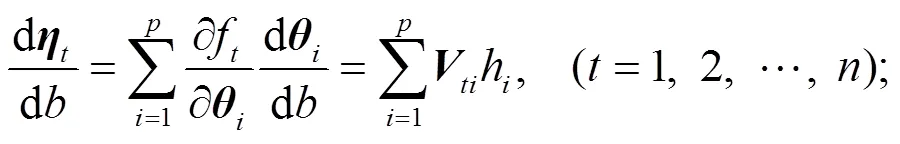
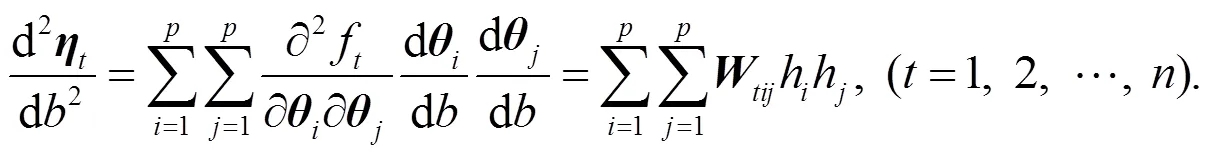
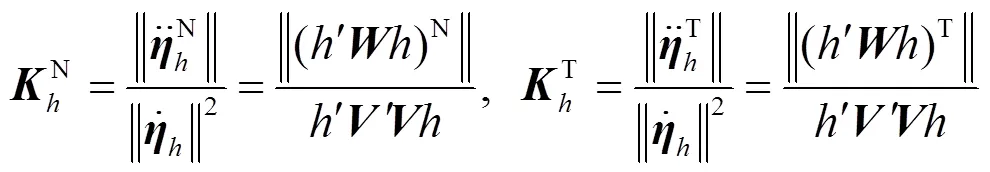
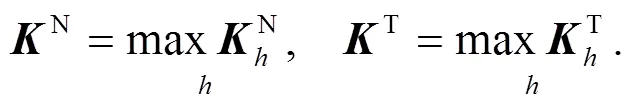
這里最大曲率反映了模型非線性程度最強的方向, 當然還可以類似地定義沿各方向的平均曲率, 它反映了平均意義上的模型非線性程度.

定理1 模型(1)的最大固有曲率為:

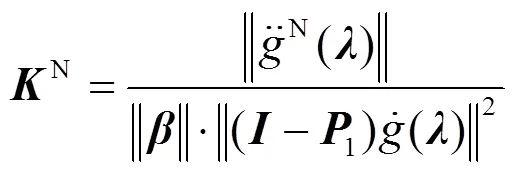
證明過程略(文獻[1]中有類似的證明).

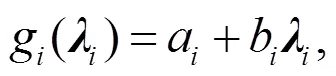
探究1 Fieller—Creasy模型:

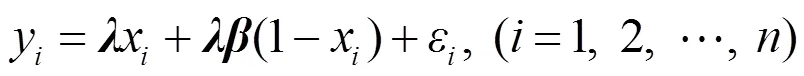
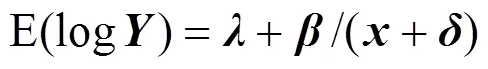
2 部分非線性模型的局部非線性度量

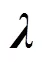
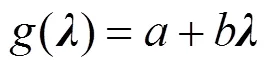
定理3 參數(shù)變換不改變局部曲率的值.

利用局部曲率來改進文獻[1—5]中使用的迭代方法.

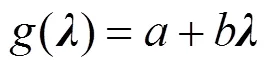
相對來說, 它顯示的是較弱的非線性程度, 這就充分體現(xiàn)了利用局部曲率度量回歸模型非線性程度的優(yōu)越性所在.

需要指出的是, 本文是利用(7)式來定義模型(1)的局部曲率, 事實上亦可定義平均意義上的局部曲率. 特別的, 可利用立體陣這一強有力的工具來定義局部曲率立體陣, 可以推測, 局部曲率立體陣相對于文獻[6—7]中的曲率立體陣應(yīng)具有足夠的優(yōu)越性.

[1] 高集體, 洪圣巖. 部分非線性模型中估計的收斂速度[J]. 數(shù)學(xué)學(xué)報, 1995, 38: 658—669.

[2] 趙慧秀. 帶有線性約束的指數(shù)族非線性回歸模型[J]. 南京師大學(xué)報: 自然科學(xué)版, 2010, 33(1): 1—5.

[3] Williams E J. Exact fiducial limits in nonlinear estimation[J]. J R statistic soc, 1962, 1324: 125—139.

[4] 肖兵. 一列非線性回歸模型的非線性度量[J]. 常德師范學(xué)院學(xué)報, 2002, 14(4): 18—20.

[5] 趙慧秀. 帶有線性約束的指數(shù)族非線性回歸模型置信域的曲率表示[J].曲阜師范大學(xué)學(xué)報, 2010, 36(1): 38—40.

[6] 邢誠. 引入模型誤差的非線性回歸模型[J]. 海洋測繪, 2009, 29(3): 1—3.

[7] 謝振東. 帶約束非線性回歸模型參數(shù)的廣義LS 估計的存在性[J]. 統(tǒng)計與決策, 2008(11): 148—149.

A measure of non-linearity of partially non-linear regression models

XIAO Bing

(Mathematics and Computational Science, Hunan University of Artsand Science, Changde 415000, China)

Based on classical methods of the non-linearity property of the non-linearity regression model, analysis of its limitation is made. This paper promotes a new method about local approximation through the discussion for the convergence of some models, which remedy the defect of the traditional ways. The asymptotic property of least square estimator and the method of iterative initial value selectionare studied. And a new trend for the method to measure the model′s non-linearity is given.

measure of non-linearity; intrinsic curvature; parameter-effects curvature; local curvature

10.3969/j.issn.1672-6146.2013.01.003

O 212.1

1672-6146(2013)01-0010-04

email: xiaobing71@163.com.

2012-12-05

湖南省自然科學(xué)基金資助項目(12JJ6004)

(責任編校:劉曉霞)