丁光濤

1 引言

振動(dòng)是自然界和工程技術(shù)領(lǐng)域中最常見的運(yùn)動(dòng)形式,是力學(xué)和物理學(xué)中一個(gè)基本的研究領(lǐng)域.經(jīng)過對振動(dòng)系統(tǒng)的理想化抽象,系統(tǒng)的振動(dòng)規(guī)律常常以微分方程來描述,因此,求振動(dòng)微分方程的積分,就是振動(dòng)理論的重要課題.最簡單的振動(dòng)系統(tǒng)是簡諧振子,對多維簡諧振子系統(tǒng)的積分問題,特別是與時(shí)間無關(guān)的積分問題仍然受到重視[1-4].近來,我們引入基本積分概念,以及利用基本積分構(gòu)造其他積分的方法,比較好地解決了簡諧振子的第一積分構(gòu)造問題,證明對n維簡諧振子系統(tǒng)總是存在2n-1個(gè)獨(dú)立的不含時(shí)的第一積分[5].由于在周圍環(huán)境和工程實(shí)際中耗散因素普遍存在,故阻尼振子問題,特別是線性阻尼振子問題不僅在經(jīng)典力學(xué)中長期受到關(guān)注,而且從20世紀(jì)30年代以來,也成為量子理論的重要研究課題[6-9].

本文研究線性阻尼振子系統(tǒng)的積分問題,利用引入線性阻尼振子的基本積分的概念,去構(gòu)造多種形式的線性阻尼振子第一積分.首先,我們導(dǎo)出一維線性阻尼振子系統(tǒng)的基本積分,并利用它們來構(gòu)造其他第一積分,特別是具有明顯物理意義的積分和不含時(shí)間的積分,并指出線性阻尼振子與簡諧振子之間的一個(gè)重要的區(qū)別;其次,將這種概念和方法推廣到多維系統(tǒng),重點(diǎn)是構(gòu)造不同類型的二維線性阻尼振子系統(tǒng)的第一積分,提出利用不同自由度的基本積分構(gòu)造其他積分的方法;給出n維情況的一般結(jié)果,證明對n維線性阻尼振子系統(tǒng)也存在2n-1個(gè)獨(dú)立的不含時(shí)的第一積分;最后,利用變量變換將一維線性阻尼振子的第一積分變換成簡諧振子的形式,并討論了n維系統(tǒng)的一般情況,即將n維線性阻尼振子問題變換成n維簡諧振子問題.

2 從線性阻尼振子的基本積分構(gòu)造第一積分

一維線性阻尼振子的運(yùn)動(dòng)微分方程為

方程的兩個(gè)第一積分為

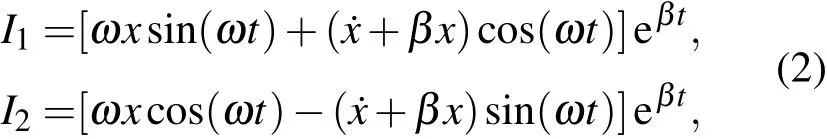
式中

將初始條件代入,即可知道I1和I2分別與初位置和初速度直接相關(guān),它們是兩個(gè)獨(dú)立的積分,我們將這兩個(gè)積分稱為基本積分.由兩個(gè)基本積分可以直接得出方程(1)的解

而且利用它們能夠構(gòu)造其他的積分.例如,

積分I3和I4分別與能量和初位相相關(guān),而I5是不含時(shí)間的積分.應(yīng)當(dāng)指出,積分I5的存在是線性阻尼振子與簡諧振子之間的一個(gè)重要區(qū)別,在簡諧振子中不含時(shí)積分是能量積分,而線性阻尼振子能量積分(5)是含時(shí)的耗散的,但是,由于積分(5)和(6)中,都含時(shí)間,因此,利用它們也可以消去時(shí)間,得到了新的不含時(shí)積分(7),原則上這個(gè)積分給出了線性阻尼振子的相軌道.當(dāng)阻尼不存在,即β=0時(shí),該積分與能量積分等價(jià).

3 多維線性阻尼振子的第一積分

3.1 二維對稱線性阻尼振子

將上述一維情況推廣到二維情況.首先討論二維對稱線性阻尼振子,其運(yùn)動(dòng)方程為

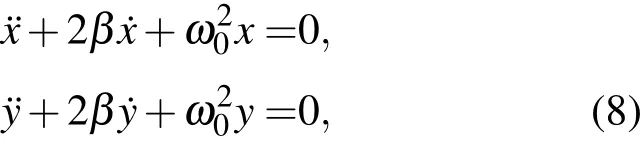
方程的四個(gè)獨(dú)立的基本積分為

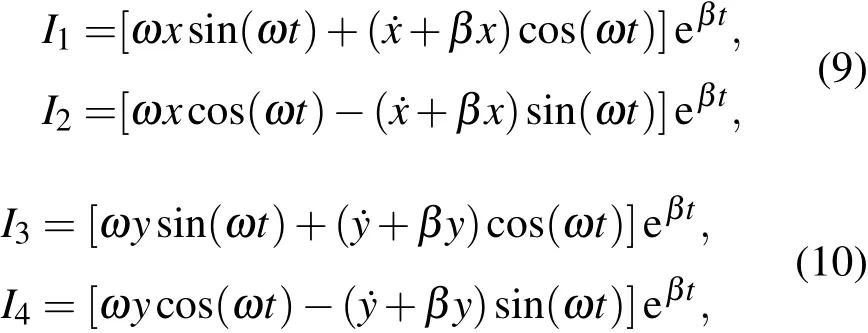
這四個(gè)獨(dú)立的積分的物理意義清楚,利用它們同樣能夠?qū)С龆S線性阻尼振子的解,也能利用它們構(gòu)造二維線性阻尼振子其他的積分.例如,與兩個(gè)分振動(dòng)對應(yīng)的四個(gè)積分

這些積分的物理意義也很明確,直接利用它們還可以得到其他積分,例如

對于二維對稱線性阻尼振子而言,這四個(gè)積分也是重要的積分.值得注意的是I10是與時(shí)間無關(guān)的積分.由于(9)和(10)式中四個(gè)第一積分的任意函數(shù)都是積分,故二維對稱線性阻尼振子的積分有任意多個(gè),其中大部分是含時(shí)的.但是,在討論系統(tǒng)運(yùn)動(dòng)時(shí),人們往往更重視尋找與時(shí)間無關(guān)的積分,如(16)式中的積分,這樣的積分代表著相空間中一個(gè)不隨時(shí)間變化的曲面,系統(tǒng)相點(diǎn)在其上運(yùn)動(dòng).對二維系統(tǒng),如果能夠?qū)С?個(gè)獨(dú)立的與時(shí)間無關(guān)的第一積分,那么就確定了系統(tǒng)的相軌道.對于二維對稱線性阻尼振子系統(tǒng)與時(shí)間無關(guān)的積分可以如下方法來構(gòu)造,例如

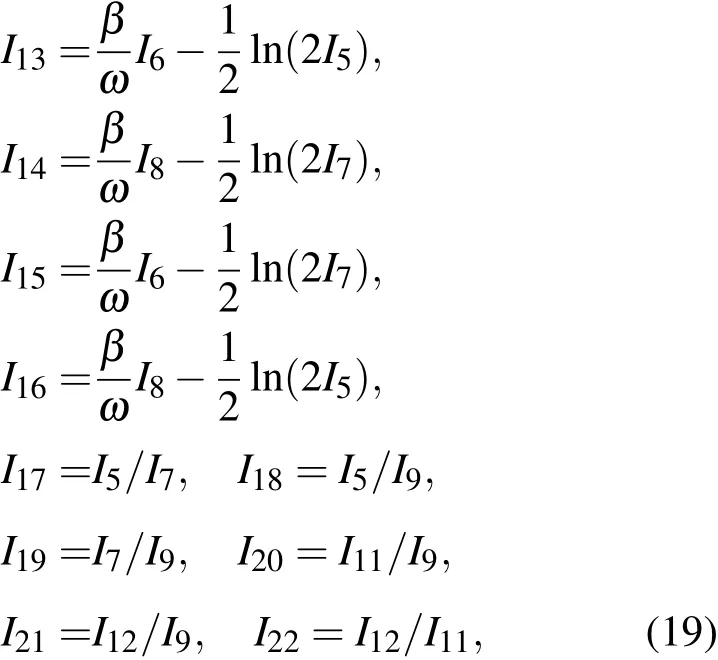
等等.這些積分中I13,I14是與(7)式中積分同一個(gè)類型的,I15,I16也是這種類型的積分,但是涉及兩個(gè)自由度.這些與時(shí)間無關(guān)的積分中獨(dú)立的只有3個(gè),例如,可選擇I10,I13,I14作為一組獨(dú)立的積分.大多數(shù)積分之間是函數(shù)相關(guān)的,例如

上述結(jié)果表明,導(dǎo)出了全部基本積分就解決了構(gòu)造二維對稱線性阻尼振子系統(tǒng)第一積分問題,證明了這種系統(tǒng)存在三個(gè)獨(dú)立的不含時(shí)的第一積分.

3.2 二維非對稱線性阻尼振子

對于二維非對稱線性阻尼振子,運(yùn)動(dòng)方程為

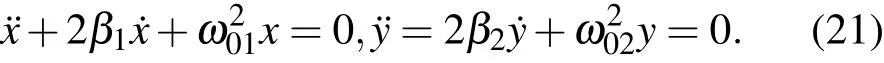
對于每一個(gè)分振動(dòng),(9)和(10)式形式的基本積分,以及(11)—(14)式類型的積分都存在,即

式中

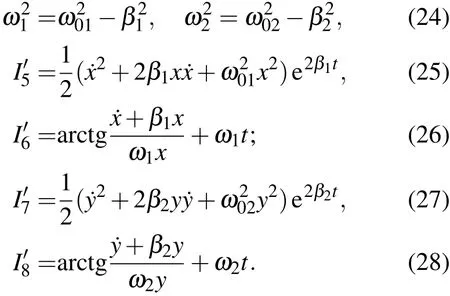
比較容易得到的涉及整個(gè)系統(tǒng)的積分為

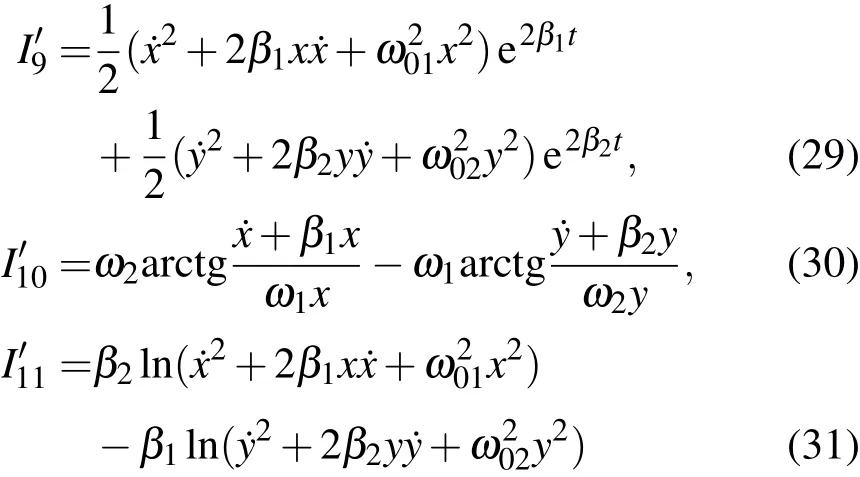
等等,其中I1′0,I1′1是不含時(shí)間的積分,當(dāng)然,還可以構(gòu)造其他的涉及和不涉及整個(gè)系統(tǒng)的積分,包括含時(shí)間的和不含時(shí)間的積分,例如,對每一個(gè)分振動(dòng)都可以導(dǎo)出(7)式類型的與時(shí)間無關(guān)的積分.值得注意的是,導(dǎo)出這些積分與兩個(gè)分振動(dòng)的頻率之比是有理數(shù)還是無理數(shù)無關(guān).對二維非對稱的線性阻尼振子三個(gè)獨(dú)立的不含時(shí)第一積分,可以選擇對應(yīng)著兩個(gè)自由度的(7)式類型的積分,再從(30)和(31)式中任意選擇一個(gè)積分.綜上所述,我們利用直接構(gòu)造方法證明了不同類型的二維線性阻尼振子總是存在三個(gè)獨(dú)立的不含時(shí)第一積分.還應(yīng)當(dāng)指出,與一維情況相似,由于線性阻尼振子基本積分中存在兩個(gè)與時(shí)間相關(guān)的因子,故不論是一維情況,還是二維情況,線性阻尼振子比簡諧振子多一種消去時(shí)間的方法,如積分I7,I13,I15I′11等.

3.3 n維線性阻尼振子

在上述一維二維線性阻尼振子從基本積分構(gòu)造其他積分的基礎(chǔ)上,進(jìn)一步討論n維系統(tǒng)獨(dú)立的不含時(shí)積分的構(gòu)造問題.設(shè)系統(tǒng)運(yùn)動(dòng)微分方程為

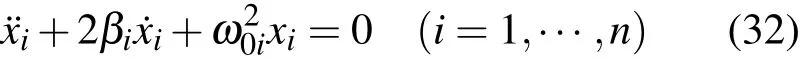
系統(tǒng)的2n個(gè)基本積分是

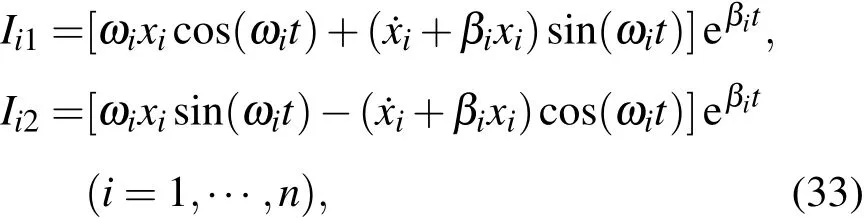
式中

我們利用直接構(gòu)造法證明系統(tǒng)存在2n-1個(gè)獨(dú)立的不含時(shí)的第一積分.首先,對每一個(gè)自由度都可以構(gòu)造如下的第一積分

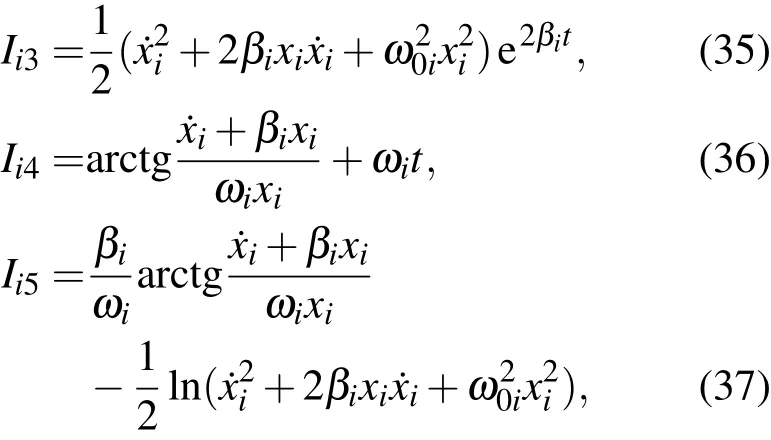
顯然,(37)式中n個(gè)不含時(shí)第一積分是獨(dú)立的.其次,利用不同的自由度的基本積分構(gòu)造其余n-1個(gè)不含時(shí)第一積分.為了討論簡明有序,我們選取第一個(gè)自由度為基準(zhǔn),假設(shè)存在m個(gè)自由度的振動(dòng)的參數(shù)βk和ωk(k=1,···,m)相同,其余的 n-m個(gè)自由度振動(dòng)參數(shù) βj和 ωj(j=m+1,···,n)與第一個(gè)自由度振動(dòng)參數(shù)β1和ω1不同(至少有一個(gè)參數(shù)不同).由前m個(gè)自由度可以構(gòu)造m-1個(gè)不含時(shí)積分

利用后面n-m個(gè)自由度可以構(gòu)造n-m個(gè)不含時(shí)積分

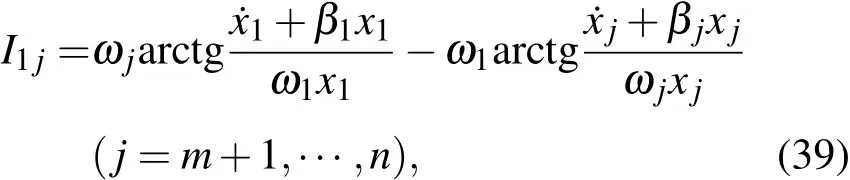
(38)和(39)式中n-1個(gè)積分也是獨(dú)立的,還應(yīng)當(dāng)指出,它們實(shí)際上可以統(tǒng)一地寫成(39)式的形式.(37)—(39)式中2n-1個(gè)積分構(gòu)成了n維線性阻尼振子系統(tǒng)一組獨(dú)立的不含時(shí)的第一積分.當(dāng)然,還可以利用其他函數(shù)形式的不含時(shí)積分構(gòu)成2n-1個(gè)獨(dú)立的積分,例如,根據(jù)情況可以將上述積分中的某些積分代以(17),(18)或(31)式類型的積分.

4 從線性阻尼振子到簡諧振子的變換

經(jīng)典力學(xué)中簡諧振子系統(tǒng)是非常重要的系統(tǒng),其運(yùn)動(dòng)規(guī)律研究得十分深入;量子力學(xué)中情況也類似,簡諧振子的量子化是一個(gè)完全解決的問題[1,2,4].然而,從數(shù)學(xué)表示上來看,簡諧振子與線性阻尼振子之間不是絕然分開的,它們之間可以相互變換.利用變量變換方法能夠?qū)⒕€性阻尼振子的微分方程和第一積分變換成為簡諧振子形式的,這個(gè)變換將利于對線性阻尼振子問題的研究,根據(jù)前面得到的結(jié)果,我們需要對基本積分完成這樣的變換.

首先研究一維情況,引入與時(shí)間相關(guān)的變換

方程(1)可以寫成如下等效的簡諧振子的形式

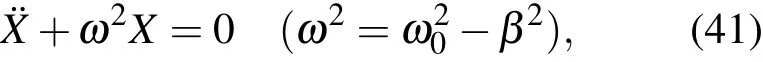
(2)式中兩個(gè)積分變換成

這正是簡諧振子的第一積分.顯然,通過變換(40)式的逆變換,(42)式中兩個(gè)積分仍變換為(2)式中的兩個(gè)積分.

上述變換可以直接推廣到多維情況,對n維線性阻尼振子(32)式,引入變換

則方程(32)和對應(yīng)的2n個(gè)基本積分都變換成簡諧振子形式的,即

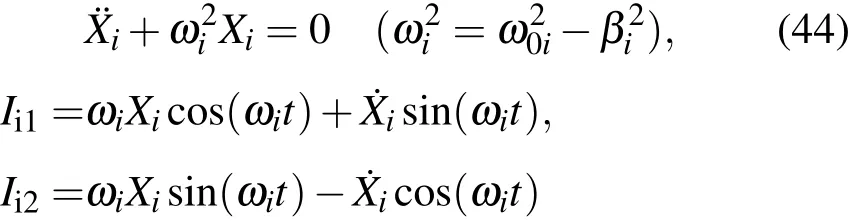
利用變換(43)式的逆變換從(45)式中2n個(gè)簡諧振子形式的積分就得到(33)式中2n個(gè)線性阻尼振子的基本積分;由簡諧振子基本積分構(gòu)成的其他積分也逆變換成為線性阻尼振子的對應(yīng)積分.然而,必須指出的是,線性阻尼振子的基本積分(33)式可以通過變換(43)式得到簡諧振子基本積分(45)式,由基本積分構(gòu)成的積分(35)和(36)式也可以直接變換成簡諧振子的對應(yīng)積分.但是,(37)式類型的線性阻尼振子積分直接利用變換(43)式得到的結(jié)果,必須經(jīng)過進(jìn)一步變換才能成為簡諧振子形式的積分.將(43)式代入(37)式得到

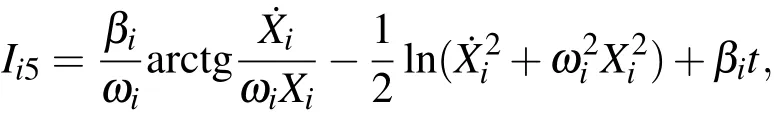
上式不能稱為簡諧振子形式的積分.但是,利用積分(36)式,可以導(dǎo)出

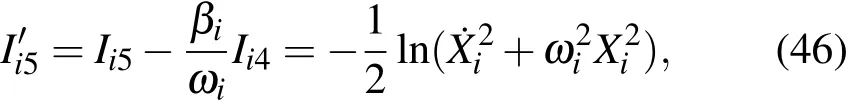
這種積分與簡諧振子的能量積分等價(jià).這種情況的出現(xiàn),與我們前面指出的由于線性阻尼振子基本積分中存在兩種與時(shí)間相關(guān)的因子,故線性阻尼振子情況比簡諧振子情況多一種消去時(shí)間的方法相關(guān);這就是說,由于阻尼因素的存在,從物理本質(zhì)上線性阻尼振子與簡諧振子之間存在著區(qū)別.

5 結(jié)論

1)本文以新的思路對線性阻尼振子系統(tǒng)第一積分進(jìn)行深入的研究,即導(dǎo)出直接與初始條件相關(guān)的基本積分后,再利用它們構(gòu)造線性阻尼振子的其他第一積分,包括不顯含時(shí)間的第一積分.這種處理方法可以應(yīng)用于一維系統(tǒng)和多維系統(tǒng),包括對稱和非對稱系統(tǒng).

2)通過直接構(gòu)造法證明,二維線性阻尼振子系統(tǒng),無論是對稱的還是非對稱的,都存在并可以實(shí)際構(gòu)造出三個(gè)不顯含時(shí)間的第一積分;n維線性阻尼振子系統(tǒng)存在2n-1個(gè)獨(dú)立的不顯含時(shí)間的第一積分.

3)通過變量變換,將線性阻尼振子方程和第一積分變換成簡諧振子形式的,這樣就使得處理線性阻尼振子的問題,包括經(jīng)典力學(xué)和量子力學(xué)問題,得到簡化.研究表明,對簡諧振子的第一積分能夠利用變量變換直接變成對應(yīng)的線性阻尼振子的結(jié)果,但是,有些線性阻尼振子的第一積分利用變量變換導(dǎo)出對應(yīng)的簡諧振子的結(jié)果時(shí),需要利用其他第一積分.

[1]Goldstein H,Poole C,Salko J 2005 Classical Mechanics(3rd Ed.)(Beijing：Higher Education Press)

[2]Li D M,Cheng C M 2006 Classical Mechanics(Beijing：Higher Education Press)(in Chinese)[李德明,陳昌民2006經(jīng)典力學(xué)(北京：高等教育出版社)]

[3]Lou Z M,Mei F X 2012 Acta Phys.Sin.61 110201(in Chinese)[樓智美,梅鳳翔2012物理學(xué)報(bào)61 110201]

[4]Zeng J Y 2001 Quantum Mechanics(Beijing：Science Press)(in Chinese)[曾謹(jǐn)言2001量子力學(xué)(北京：科學(xué)出版社)]

[5]Dekker H 1981 Phys.Rep.80 1

[6]Um C I,Yean K H,George T F 2002 Phys.Rep.362 63

[7]Pen H W 1980 Acta Phys.Sin.29 1084(in Chinese)[彭桓武1980物理學(xué)報(bào)29 1084]

[8]Zhu R Z 1981 Acta Phys.Sin.30 1410(in Chinese)[朱如曾1981物理學(xué)報(bào)30 1410]

[9]Ling R L,Feng J F 1998 Acta Phys.Sin.47 1952(in Chinese)[凌瑞良,馮金福1998物理學(xué)報(bào)47 1952]