Positive Solutions for Fourth-order Delay Dif f erential Equation of Boundary Value Problem with p-Laplacian
ZHANG Yu-chuan,ZHOU Zong-fu
(School of Mathematical Sciences,Anhui University,Hefei 230039,China)
Positive Solutions for Fourth-order Delay Dif f erential Equation of Boundary Value Problem with p-Laplacian
ZHANG Yu-chuan,ZHOU Zong-fu
(School of Mathematical Sciences,Anhui University,Hefei 230039,China)
In this work,we investigate the following fourth-order delay dif f erential equation of boundary value problem with p-Laplacian
By using Schauder f i xed-point theorem,some sufficient conditions are obtained which guarantee the fourth-order delay dif f erential equation of boundary value problem with p-Laplacian has at least one positive solution.Some corresponding examples are presented to illustrate the application of our main results.
boundary value problem;delay;positive solution;p-Laplacian;schauder f i xedpoint theorem
§1.Introduction
As is known,boundary value problems arise in many engineering and scientif i c disciplines such as physics,chemistry,biology,economics,control theory,signal and image processing, biophysics,blood f l ow phenomena,aerodynamics,f i tting of experimental data,etc[15].In recent years,boundary value problems of dif f erential equation with p-Laplacian have been addressed by many scholars,we refer to the works[68].Alves[9]established the existence of nontrivial solutions for a degenerate p-Laplacian equation by using variational methods,Peng[10]discussedthe existence of ω-periodic solutions of a class of Rayleigh equations with p-Laplacian,Bueno, Ercole,Ferreira and Zumpano[11]investigated a Dirichlet problem with p-Laplacian,Ahmad and Nieto[12]studied the three-point second-order integral dif f erential boundary value problems with p-Laplacian by using the monotone iterative technique.
In[13],Tian and Liu used f i xed point index theorem to research the following thrird-order three-point boundary value problem with p-Laplacian
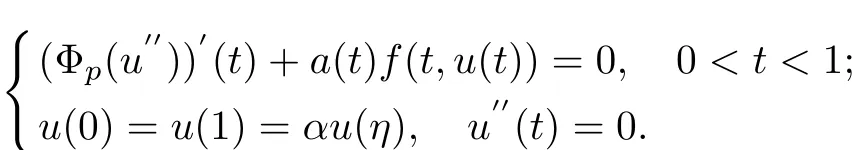
Some conditions for the existence of one or two positive solutions for the above boundary value problem with p-Laplacian are obtained.
In[14],Zhang and Ge investigated a third-order three-point boundary value problem with p-Laplacian which is as following
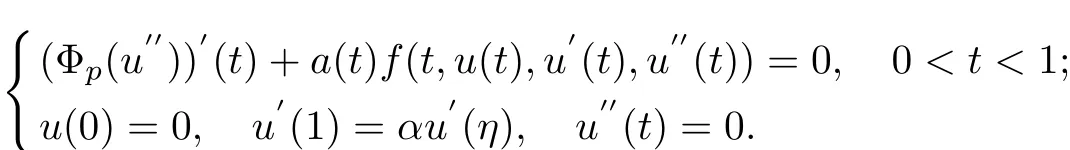
By using Avery-Peterson f i xed point theorem,they proved that there exist at least three positive solutions for the above problem,when f satisf i es some growth conditions.
As far as we know,there is fewer results on the existence of the fourth-order dif f erential equation of boundary value problem with p-Laplacian and delay dif f erential equation of boundary value problem with p-Laplacian.Motivatived by them we investigate a class of fourth-order delay dif f erential equation of boundary value problem with p-Laplacian which is as following
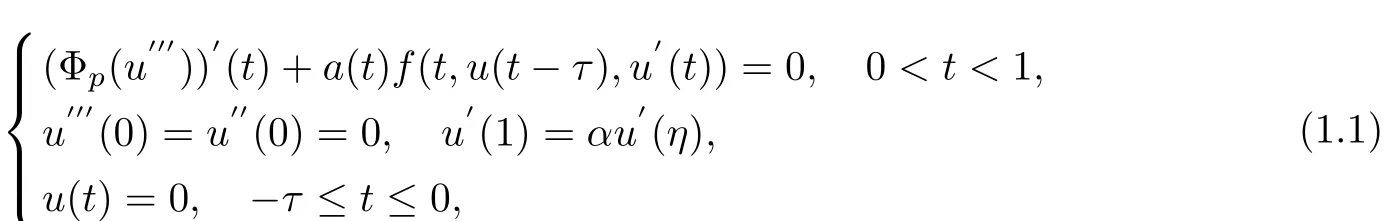
where Φp(s)=|s|p?2s,p>1,f∈C([0,1]×R+×R,R+),R+=[0,+∞),a∈C([0,1]),a(t)>0,t∈[0,1],α,η∈(0,1).
The main purpose in this work is to give some sufficient conditions,which secure the existence of solution for the fourth-order delay dif f erential equation of boundary value problem with p-Laplacian(1.1),by using the Schauder f i xed-point theorem and some techniques.Our results extend some results on boundary value problem with p-Laplacian from third-order to fourth-order.some illustrative examples will be provided to demonstrate the applications of the results of this study.
§2.Preliminaries
In this section,we give some def i nitions and fundamental facts which will be useful to prove our main results.
Def i nition 2.1A function u(t)is called a positive solution of(1.1),if it satisf i es(1.1) and u∈C([?τ,1],R+).
Let
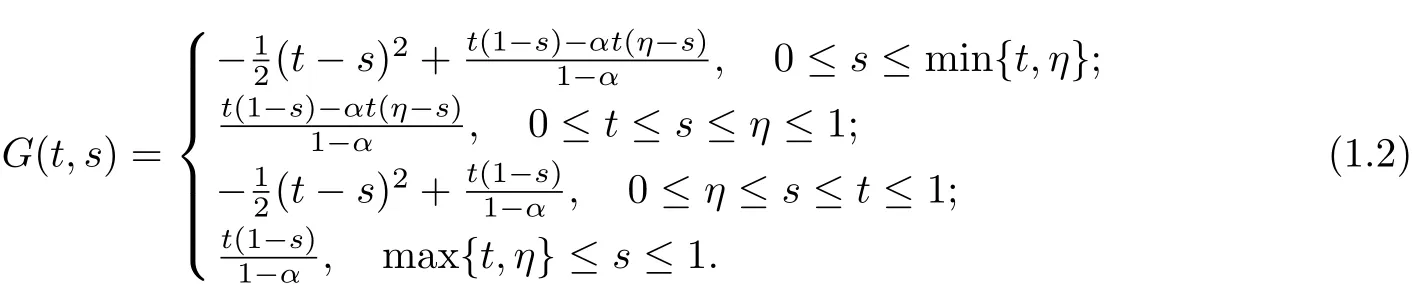
Derivative G(t,s)about t,we have
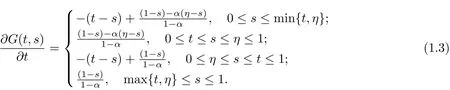
Lemma 2.1By the def i nition G(t,s),the following result holds
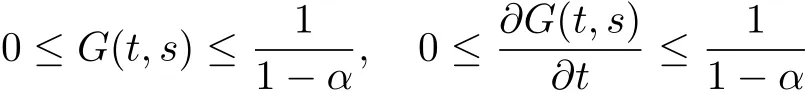
for all t,s∈[0,1].
ProofUsing the def i nition of G(t,s)in(1.2)andin(1.3),we have
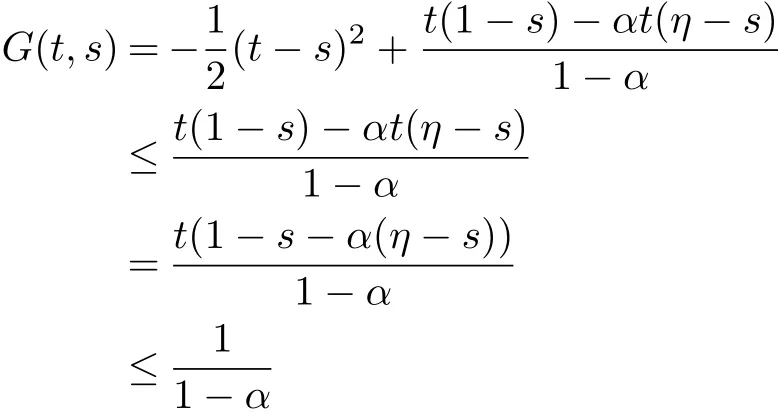
for all t,s∈[0,1]with 0≤s≤min{t,η}.
for all t,s∈[0,1]with 0≤t≤s≤η≤1.
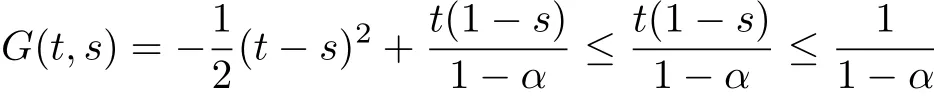
for all t,s∈[0,1]with 0≤η≤s≤t≤1.
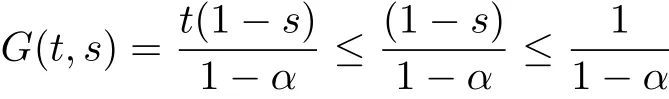
for all t,s∈[0,1]with max{t,η}≤s≤1.
By[15]we have 0≤G(t,s).Hence,we have 0≤G(t,s)is valid for all all t,s∈[0,1].s valid for all t,s∈[0,1].Next we prove
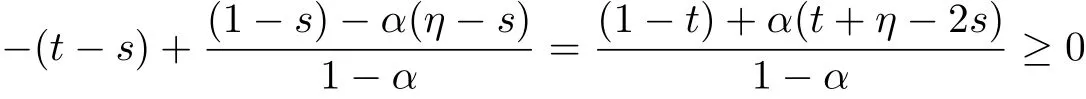
for 0≤s≤min{t,η}.
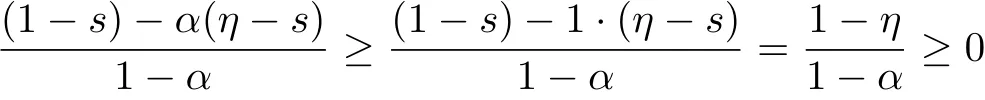
for 0≤t≤s≤η≤1.
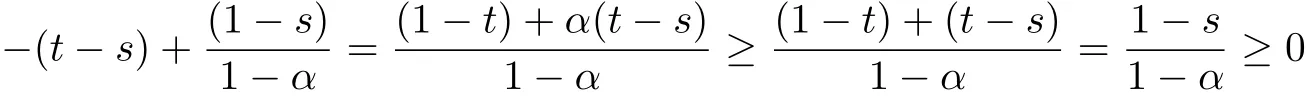
for 0≤η≤s≤t≤1.
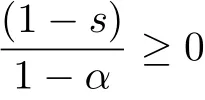
for max{t,η}≤s≤1.
Considering the following boundary value problem
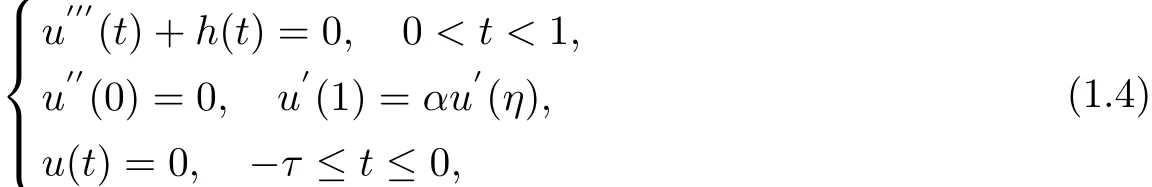
where h∈C[0,1],α,η∈(0,1).
Lemma 2.2If u(t)is a solution of the problem(1.4),then
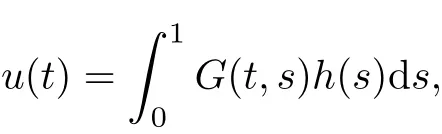
where G(t,s)is def i ned as(1.2).
ProofFrom u′′′(t)+h(t)=0,we have
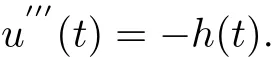
Integrating the above equality between 0 and t three times,we can obtain
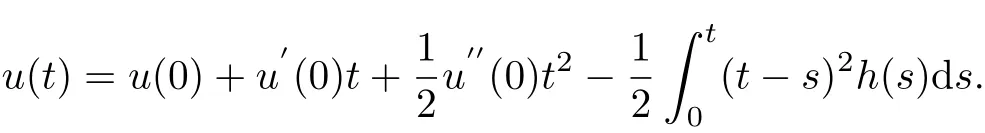
Combining with the condition of boundary value problem(1.4),we have
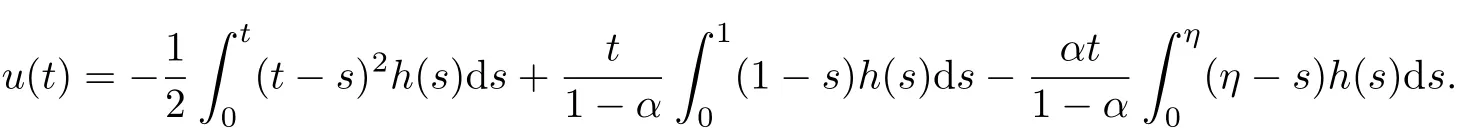
Lemma 2.3Considering the following boundary value problem

where h∈C([0,1],R+),α,η∈(0,1).
Assume that u(t)is a solution of the problem(1.5),then u(t)= (x)dx)ds, where G(t,s)is def i ned as(1.2)andis an inverse function of Φp.
ProofIf u(t)is a solution of the problem(1.5),then we have

Integrating the above equality between 0 and t with u′′′(0)=0,we can obtain
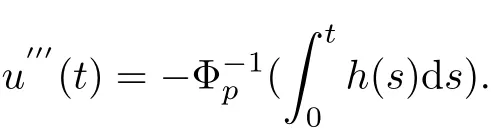
According to Lemma 2.2 we have u(t)=h(x)dx)ds.The proof of Lemma 2.3 is completed.
Lemma 2.4[16]Let E be a Banach space,K is a bounded convex and nonempty set of in E,if A:K?→K is a completely continuous operator,then there exists a point x∈K, satisf i es Ax=x.
For convenience,we def i ne E={u∈C1[?τ,1]:u(t)=0,t∈[?τ,0]},then E is a Banach space when endowed with the norm‖u‖=|u′(t)|.We def i ne an operator T:E?→E,which is as following
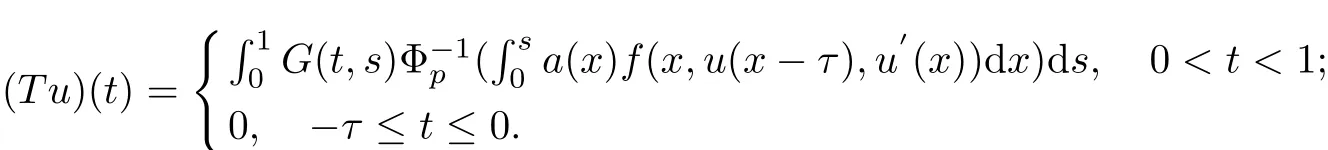
It is easy for us to check that u(t)is a solution of the problem(1.1)if and only if u(t)is a f i xed point of T.
§3.Main Results
In this section,we give our main results.By means of Schauder f i xed-point theorem,some sufficient conditions are obtained,which guarantee the fourth-order delay dif f erential equation of boundary value problem with p-Laplacian has at least one positive solution.
Theorem 3.1Let f:[0,1]×R+×R?→R+be continues functions.Suppose that the following conditions are satisf i ed.
[H1]f(t,0,0)=0 is valid for all t∈[0,1],|f(t,x1,y1)?f(t,x2,y2)|≤?1(t)|x1?x2|+?2(t) |y1?y2|for all t∈[0,1],x1,x2∈R+,y1,y2∈R,where ?i:[0,1]?→(0,∞)is continuous function(i=1,2).
[H2]There exists a real positive number δ such that
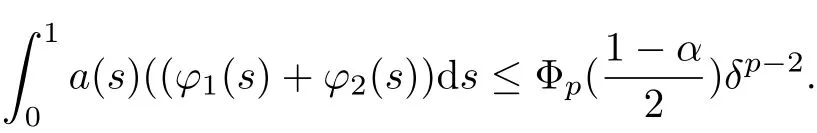
Then the problem(1.1)has at least one positive solution.
ProofLet us set a bounded convex and nonempty set K and prove T:K?→K is a completely continuous operator,where K is def i ned as follows

(1)We prove T:K?→K.By the def i nition of T,we know that(Tu)(t)≥0,in view of the def i nition of G(t,s)and Φpwe have Tu is a continuous function.In addition we can check T(E)?E.For any u∈K,t∈[0,1],we have
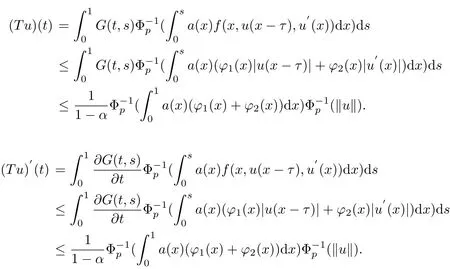
Hence,

According to the def i nition of K and the condition[H2]we have
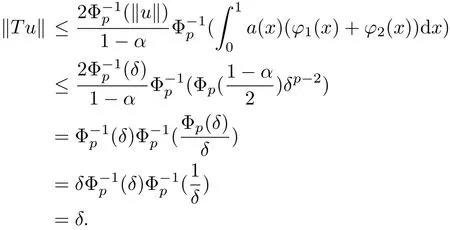
By the above proof we have T(K)?K.
(2)We prove T:K?→K is a completely continuous operator.Let{un}?K with‖un?u0‖tending to zero when n tending to inf i nity,then{un}is a bounded set.We assume that‖un‖≤d(d≤η),n=0,1,2,···,then we have

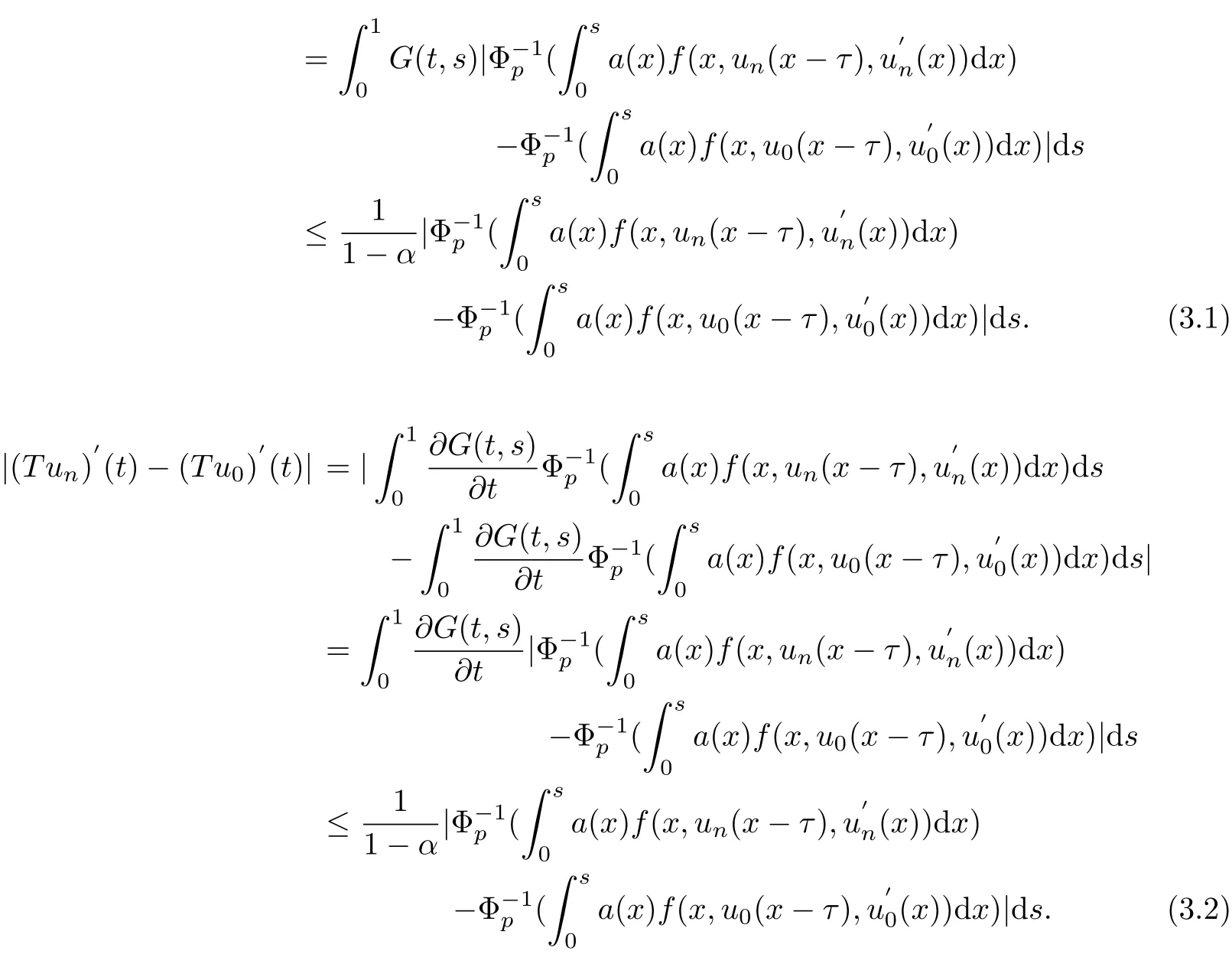
Hence,by(3.1)and(3.2)we have‖Tun?Tu0‖?→0(n?→+∞).Thus T:K?→K is uniformly continuous operator.
In view of the continuity of G(t,s),we have that for any number ξ>0,there exists a number δ>0,such that
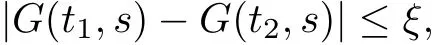
where t1,t2∈[0,1],s∈[0,1]with|t1?t2|<δ.For any u∈K then we have
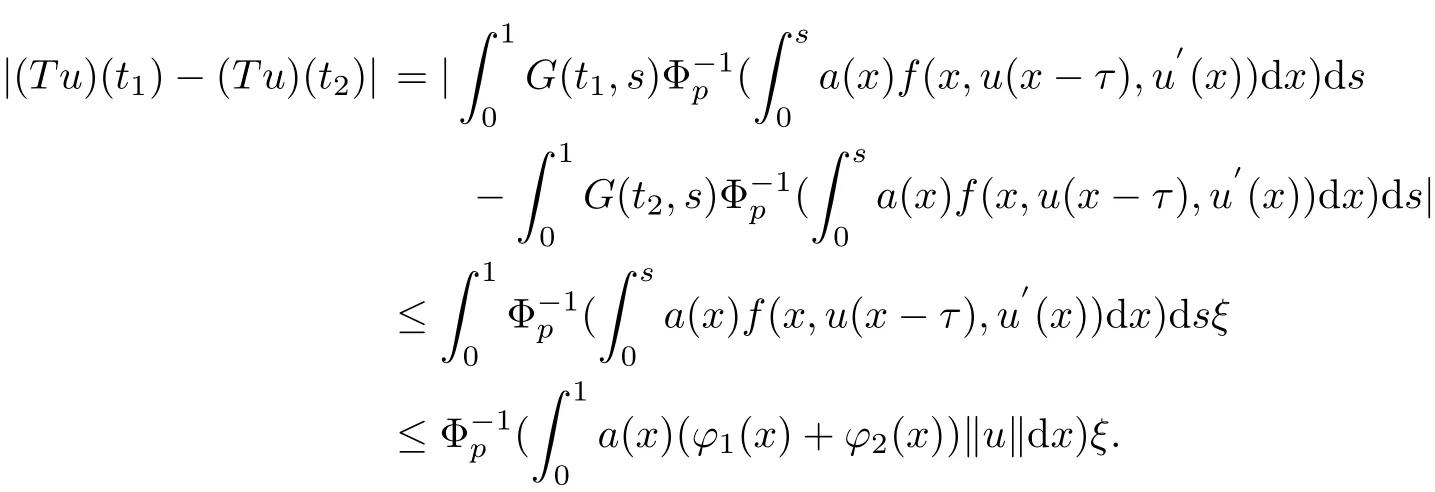
According to H1,H3we can prove that T is equicontinuous.Obviously TK is uniformly bounded since TK?K.Thus T is completely continuous.By the Lemma 2.4 Schauder f i xedpoint theorem implies the problem(1.1)has at least one positive solution.The Theorem 3.1 is proved.
Theorem 3.2Let f:[0,1]×R+×R?→R+be continues functions.Suppose that the following conditions are satisf i ed.
[H3]f(t,0,0)=λ(0<λ<∞)is valid for all t∈[0,1],|f(t,x1,y1)?f(t,x2,y2)|≤?1(t)|x1?x2|+?2(t)|y1?y2|for all t∈[0,1],x1,x2∈R+,y1,y2∈R,where ?i:[0,1]?→(0,∞)is continuous function(i=1,2).
[H4]There exists a real positive number δ such that
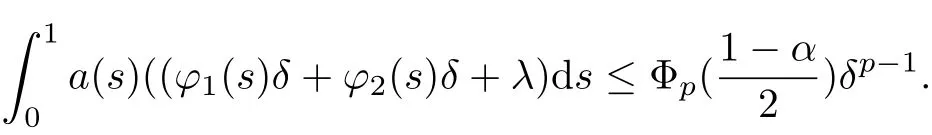
Then the problem(1.1)has at least one positive solution.
The proof of Theorem 3.2 is similar to the proof of Theorem 3.1,it is easy for us to prove it.
Example 3.1Considering the following problem
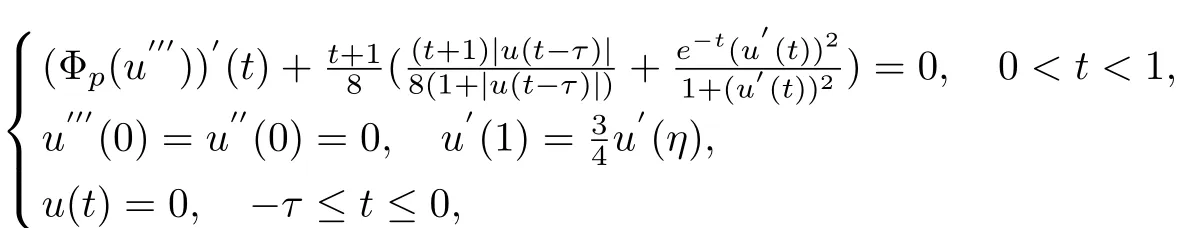
Example 3.2Considering the following problem

where Φp(s)=|s|43?2s.Notice that a(t)=the Theorem 3.2,the problem(1.1)has at least one positive solution.
The authors are grateful for the referees careful reviewing and helpful comments.Also we would like to thank the editor for his(her)encouragement and suggestions.
[References]
[1]MA Ru-run.Multiplicity of positive solutions for second-order three-point boundary value problems[J]. Computers Mathematics with Applications,2000,40:193-204.
[2]YAO Qin-liu.Existence and multiplicity of positive solutions for a class of second-order three-point nonlinear boundary value problems[J].Acta Mathematica Sinica,2002,6:1057-1064.
[3]LIU Bing.Positive solutions of a nonlinear three-point boundary value problem[J].Applied Mathematics Com-putation,2002,132:11-28.
[4]MA Ru-run.Positive solutions of a nonlinear three-point boundary value problem[J].Electronic Journal of Dif f erential Equations,1998,34:1-8.
[5]SUN Yong-ping.Positive solutions for three-order three-point nonhomogeneous boundary value prblems[J]. Appl Math Lett,2009,22:45-51.
[6]CHAI Guo-qing.Positive solutions for boundary value problem of fractional dif f erential equation with p-Laplacian operator[J].Boundary Value Problems,2012,1(18):1687-2770.
[7]WANG Jing.The existence of positive solutions for the one-dimesional p-Laplacian[J].Proc Amer Math Soc,1997,125(8):2275-2283.
[8]HE Xiao-ming,GE Wei-gao.Twin positive solutions for the one-dimensional p-Laplacian boundary value problems[J].Nonlinear Analysis,2004,56(7):975-984.
[9]ALVES C O.Existence of solution for a degenerate p(x)-Laplacian equation in Rn[J].J Math Anal Appl, 2008,345:731-742.
[10]PENG Shi-guo.Periodic solutions for p-Laplacian neutral Rayleigh equation with a deviating argument[J]. Nonlinear Anal,2008,69:1675-1685.
[11]BUENO H,ERCOLE G,FERREIRA W,et al.Existence and multiplicity of positive solutions for the p-Laplacian with nonlocal coefficient[J].J Math Anal Appl,2008,343:151-158.
[12]AHMAD B,NIETO J J.The monotone iterative technique for three-point second-order integral dif f erential boundary value problems with p-Laplacian[J].Boundary Value Problems,doi:10.1155/2007/57481.
[13]TIAN Yu-sheng,LIU Chun-gen.The existence of positive solutions for a three-point singular boundary value problem with a p-Laplace operator[J].Chinese Journal of Engineering Mathematics,2009,26(3):519-527.
[14]ZHANG Li-xin,GE Wei-gao.Existence of three positive solutions for three-order dif f erential equations of boundary value problem with p-Laplacian[J].Systems Science and Mathematical Sciences,2011,31(7): 837-844.
[15]GUO Da-jun.Nonlinear Function Analysis[M].Jinan:Science and Technology Press,2004.
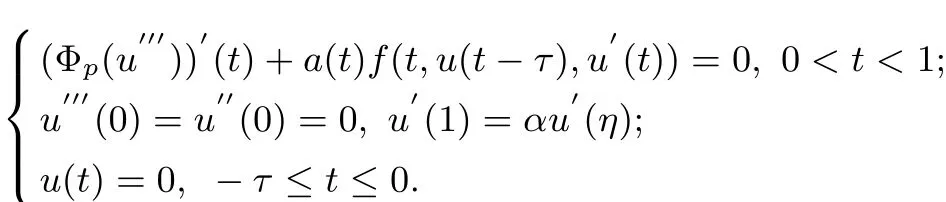
tion:34B15,34B18,34B27
O175.8Document code:A
1002–0462(2014)02–0171–09
date:2012-03-06
Supported by the National Natural Science Foundation of China(10801001);Supported by the Natural Science Foundation of Anhui Province(1208085MA13,KJ2009A005Z)
Biography:ZHANG Yu-chuan(1985-),male,native of Nanyang,Henan,M.S.D.,engages in boundary value problem.
 Chinese Quarterly Journal of Mathematics2014年2期
Chinese Quarterly Journal of Mathematics2014年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- Group Twisted Tensor Biproducts over Hopf Group Coalgebras
- A Class of Solvable Lie Algebras and Their Hom-Lie Algebra Structures
- A New Nonlinear Integrable Couplings of Yang Equations Hierarchy and Its Hamiltonian Structure
- Cyclic Codes overF2+uF2+vF2
- The Existence and Uniqueness of the Solution for Periodical Boundary Value Problems of 2kth Order Dif f erential Equations with Resonance
- On the Characterization of Cyclic Codes over RingF2+uF2+vF2
