On the Characterization of Cyclic Codes over RingF2+uF2+vF2
ZHANG Xiao-yan
(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China)
On the Characterization of Cyclic Codes over RingF2+uF2+vF2
ZHANG Xiao-yan
(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China)
In this work,we investigate the cyclic codes over the ringF2+uF2+vF2.We fi rst study the relationship between linear codes overF2+uF2+vF2and that overF2. Then we give a characterization of the cyclic codes overF2+uF2+vF2.Finally,we obtain the number of the cyclic code overF2+uF2+vF2of length n.
linear code;cyclic code;Gray map;generator matrix
§1.Introduction
In 1994,Hammons et al[1]studied how to construct some nonlinear codes by applying the Gray map to cyclic codes over?4.Since then the study of cyclic codes over rings has greatly intensi fi ed,many papers have dealt with cyclic codes over various types rings(see[4-6]). Recently,cyclic codes over the ringF2+uF2+vF2+uvF2have been considered by Yildiz and Karadeniz in[2],where some good binary codes have been obtained as the images under two Gray maps.Some results about cyclic codes overF2+vF2were given by Zhu et al in[3], where it is shown that cyclic codes over the ring are principally generated.
In this work,we will let R denoteF2+uF2+vF2,where u2=uv=vu=0,v2=v.The ring R is a fi nite principal ideal ring,i.e.,R is a fi nite Frobenius ring,not a fi nite chain ring. We fi rst de fi ne a Gray map from Rnto,and prove that the image of a linear code over R of length n under the Gray map is a distance-invariant linear code overF2of length 3n.Usingthis Gray map,we investigate the relationship between linear codes over R and that overF2. We give a characterization and the number of the cyclic code over R of length n.
§2.Priminarie
We f i rst recall that a linear code C over the ring R of length n is just an R-submodule of Rn.For x=(x1,···,xn),y=(y1,···,yn)∈Rn,the inner product of x,y is def i ned as follows
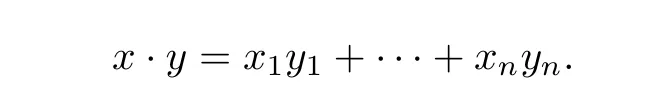
Let C be a linear code over R of length n.We def i ne C={x∈R|x·c=0,?c∈C}to be the orthogonal code of C.Notice that C⊥is linear.
In[8],it is proved that for any linear code C of length n over a f i nite Frobenius ring the following holds

For any element a+ub+vd∈R,we def i ne WL(a+ub+vd)=WH(d,d+b,a+b+d),where WHdenotes the ordinary Hamming weight for binary codes.This leads to the Gray map

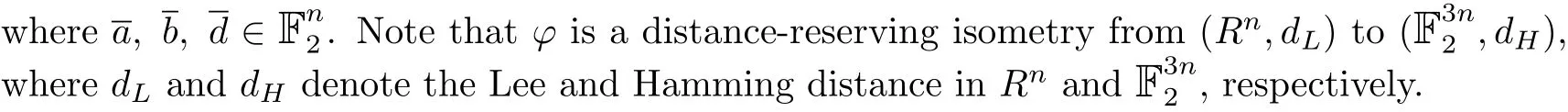
Lemma 1If C is a linear code over R of length n,size 2kand minimum Lee weight d, then ?(C)is a binary linear code with parameters[3n,k,d].
ProofLet x1=a1+ub1+vd1,x2=a2+ub2+v d2∈C,whereai,bi,di∈Fn2,i=1,2. Then

This implies that ?(C)is a linear binary code overF2.
Since the Gray map ? is an isometry from(Rn,dL)to(F32n,dH),by the de fi nition of Gray map,we get WH(?(x))=WL(x),x∈C,dH(?(x1),?(x2))=dL(x1,x2),x1,x2∈C.Then the minimum Lee weight of C is the same as the minimum Hamming weight of ?(C).
Lemma 2Let C be a liner code over R of length n.Then ?(C⊥)=?(C)⊥.
ProofLet x1=a1+ub1+vd1,x2=a2+ub2+v d2∈C be two codewords with
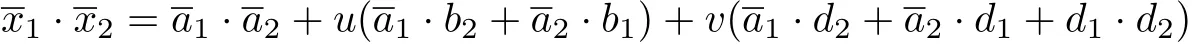
and

It is easy to check that x1·x2=0,impling ?(x1)·?(x2)=0.Therefore

But,by the de fi nition of ?,?(C)is a binary linear code of length 3n of size|C|.So,by the usual properties of the dual of binary codes,we know that|?(C)⊥|=Since R is a fi nite Frobenius ring,by(2.1),this implies

Combining(2.2)with(2.3),we get the desired equality.
§3.Linear Codes overF2+uF2+vF2
If A,B and D are codes,we denote that

and

Def i ne

and

Theorem 1Let C be a linear code of length n over R.Then ?(C)=C1?C2?C3and |C|=|C1|·|C2|·|C3|.Moreover ?(C)is linear.
ProofFor any(a1,···,an,b1,···,bn,d1,···,dn)∈?(C),take ci=(di+bi)+u(ai+ bi)+vai,i=1,2,···,n.Since ? is a bijection c=(c1,c2,···,cn)∈C,by the def i nitions of C1,C2and C3,we obtain that(a1,···,an)∈C1,(b1,···,bn)∈C2and(d1,···,dn)∈C3. Therefore(a1,···,an,b1,···,bn,d1,···,dn)∈C1?C2?C3.
On the other hand,for any(a1,···,an,b1,···,bn,d1,···,dn)∈C1?C2?C3,where (a1,···,an)∈C1,(b1,···,bn)∈C2and(d1,···,dn)∈C3,we have ?((b+d)+u(b+a)+va)= (a,b,d),which gives C1?C2?C3??(C).Hence ?(C)=C1?C2?C3.The second result is easily verif i ed.
Corollary 2If G1,G2and G3are generator matrices of binary linear codes C1,C2and C3,respectively,then the generator matrix of C is

Moreover,if G1=G2=G3,then G=G1.
ProofSince G1,G2and G3are the generator matrices of binary linear codes C1,C2and C3,respectively,the generate matrix of ?(C)=C1?C2?C3is

By the Theorem 1 the generator matrix of C is

Corollary 3If ?(C)=C1?C2?C3,then C can be uniquely expressed as C=(u+ v)C1⊕uC2⊕C3.Moreover dL(C)=min{dH(C1),dH(C2),dH(C3)},where dH(Ci)denotes the minimum Hamming weight of a binary code Ci.
ProofBy the generator matrix of C,we have C=(u+v)C1⊕uC2⊕C3.It is easy to see that the expression is unique.Because ? is an weight-preserving map,

By Lemma 2,for the linear code C over R,we have ?(C⊥)=?(C)⊥.In[7],we know that ?(C)⊥=.Thus we have proved the following corollary
CorollaryIf C=(u+v)C1⊕uC2⊕C3,then C⊥=(u+v)
§4.Cyclic Codes overF2+uF2+vF2
A cyclic shift on R is a permutation τ such that τ(c0,c1,···,cn?1)=(cn?1,c0,···,cn?2). A linear code C over R of length n is said to be a cyclic code,if it is invarant under the cyclic shift,i.e.,τ(C)=C.
Theorem 5Let C=(u+v)C1⊕uC2⊕C3be a cyclic code over R of length n.Then C is a cyclic code over R of length n if and only if C1,C2and C3are all cyclic codes overF2.
ProofFor any c=(c0,c1,···,cn?1)∈C,we can write its components as ci=(di+ bi)+u(ai+bi)+vai,i=0,1,···,n?1,where ai,bi,di∈F2,i=0,1,···,n?1.Let a=(a0,a1,···,an?1),b=(b0,b1,···,bn?1)and d=(d0,d1,···,dn).Then a∈C1,b∈C2and d∈C3.If C1,C2and C3are cyclic codes overF2,respectively,then τ(a)∈C1,τ(b)∈C2and τ(d)∈C3.Hence τ(c)=(u+v)τ(a)+uτ(b)+τ(d)∈C,which means that C is a cyclic code over R.
Conversely,for any a=(a0,a1,···,an?1)∈C1,b=(b0,b1,···,bn?1)∈C2and d= (d0,d1,···,dn)∈C3.Let ci=(di+bi)+u(ai+bi)+vai,i=0,1,···,n?1.Then c= (c0,c1,···,cn?1)∈C.If C is a cyclic code over R,then τ(c)=(u+v)τ(a)+uτ(b)+τ(d)∈C. It follows that ?(τ(c))=(τ(a),τ(b),τ(d))∈?(C)=C1?C2?C3.Thus τ(a)∈C1,τ(b)∈C2and τ(d)∈C3.Therefore,C1,C2and C3are all cyclic codes overF2.
Theorem 6Let xn?1∈F2[x]be uniquely expressed as xn?1=),where pi(x) F are pariwise relativelyprime nonzero polynomials over2.Then the number of the cyclic code over R of length n is si+1)3
§5.Conclusion
In this work,we de fi ne a Grap map ? from Rntoand prove that the image of a linear code C over R of length n under the Gray map ?(C)is a distance?invariant linear code overF2of length 3n.Since R is a fi nite Frobenius ring,we obtain that ?(C⊥)=?(C)⊥.By using Gray map ?,we give a characterization of the cyclic codes over R of length n.Moreover,when the code length n is given,will this mean better binary codes?It is worthy of further consideration.
[1]HAMMANS A R,KUMAR P V,CALDERBANK A R,et al.The?4linearity of Kerdock,Preparata, Goethals and related codes[J].IEEE Trans Inform Theory,1994,40:301-319.
[2]YILDIZ B,KARADENNIZ S.Cyclic code overF2+uF2+vF2+uvF2[J].Des Codes Crypt,2010,58: 273-287.
[3]ZHU Shi-xin,WANG Yang,SHI Min-jia.Some results on cyclic codes overF2+vF2[J].IEEE Trans Inform Theory,2010,56(4):1680-1684.
[4]ABUALRUB T,SIAP I.Cyclic codes over the rings?2+u?2and?2+u?2+u2?2[J].Des Codes Crypt, 2007,42:273-287.
[5]BONNECUZE A,UDAYA P.Cyclic codes and self-dual codes overF2+uF2[J].IEEE Trans Inform Theory, 1999,45(4):1250-1255.
[6]DINH H Q,LOPEZ-PERMOUTH S R.Cyclic and negacrclic codes over f i nite chain rings[J].IEEE Trans Inform Theory,2004,50(8):1728-1744.
[7]LIU Xiu-sheng.MDR codes and self-duals on Cartesian product codes[J].Journal on Communications, 2010,31:123-125.
[8]WOOD J.Duality for modules over f i nite rings and applications to coding theory[J].Amer J Math,1999, 121:555-575.
tion:94B05,94A15
CLC number:O157.4Document code:A
1002–0462(2014)02–0210–05
date:2012-06-25
Supported by the Scientif i c Research Foundation of Education Department of Hubei Province(B2013069);Supported by the National Science Foundation of Hubei Polytechnic University of China(12xjz14A,11yjz37B)
Biography:ZHANG Xiao-yan(1979-),female,native of Huangshi,Hubei,an associate professor of Hubei Polytechnic University,engages in algebra coding.
 Chinese Quarterly Journal of Mathematics2014年2期
Chinese Quarterly Journal of Mathematics2014年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- Group Twisted Tensor Biproducts over Hopf Group Coalgebras
- A Class of Solvable Lie Algebras and Their Hom-Lie Algebra Structures
- Positive Solutions for Fourth-order Delay Dif f erential Equation of Boundary Value Problem with p-Laplacian
- A New Nonlinear Integrable Couplings of Yang Equations Hierarchy and Its Hamiltonian Structure
- Cyclic Codes overF2+uF2+vF2
- The Existence and Uniqueness of the Solution for Periodical Boundary Value Problems of 2kth Order Dif f erential Equations with Resonance
