Sierpiski圖與Sierpiski gasket圖的條件著色?
宋興坤,梁曉東
(新疆大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院,新疆烏魯木齊830046)
0 引言
(C1).若uv∈E(G),則c(u)=c(v);
(C2).?v∈V(G),|c(N(v))|min{r,d(v)}.
可以正常(k,r)-條件著色的最小k稱為G的條件色數(shù),記為χr(G).
1 預(yù)備知識(shí)
定義1[3]
(i)ut=vt(t=1,2,···,h?1);
(iii)ut=vh和uh=vt(t=h+1,h+2,···,n).
設(shè)i∈{1,2,···,k},則頂點(diǎn)(i···i)叫做圖S(n,k)的極點(diǎn);圖S(n+1,k)i是由圖S(n+1,k)中標(biāo)記為(i···)這樣的頂點(diǎn)生成的,顯然圖S(n+1,k)i與圖S(n,k)同構(gòu).
下面給出條件著色的一些性質(zhì)與相關(guān)引理.
性質(zhì)1[6]當(dāng)圖G是連通圖,則下列條件保持成立:
(iv)如果圖H是圖G的一個(gè)子圖,即H?G,則
引理1[6]如果所有度數(shù)大于1的點(diǎn)都在三角形中,則稱圖G是正規(guī)的,即
引理2[6]當(dāng)n1,圖Sn是唯一3可著色的.
引理3當(dāng)圖Sn的極點(diǎn)取相同顏色時(shí),圖Sn是唯一4可著色的.
證明當(dāng)n=2時(shí),極點(diǎn)取相同的顏色時(shí),{1,2},{1,3},{2,3}組成K3,三點(diǎn)不能取與極點(diǎn)相同的顏色,圖S2點(diǎn)著色c只有以下一種著色:c((11))=c((22))=c((33))=1;c({1,2})=2;c({1,3})=3;c({2,3})=4,如圖2,所以圖S2唯一4可著色.
假設(shè)n=k時(shí),對(duì)圖Sk結(jié)論都成立,當(dāng)n=k+1時(shí),因?yàn)閳DSk與圖同構(gòu),即則圖的所有極點(diǎn)取相同的顏色時(shí),圖Sk+1是唯一可由圖Sk的四種顏色著色.所有結(jié)論成立.
2 主要結(jié)果
定理1若n≥2,r≥1,則
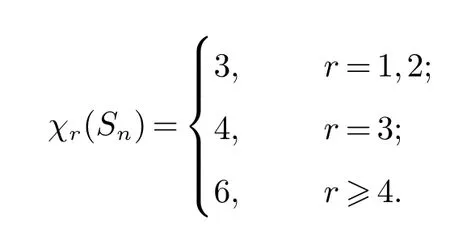
證明
(i) 當(dāng)r=1時(shí),由性質(zhì)1-(i)與引理2,得χ1(Sn)=χ(Sn)=3;
(ii) 當(dāng)r=2時(shí),因?yàn)閳DSn中任意邊都在K3中,根據(jù)引理1,則有χ2(Sn)=χ1(Sn)=3;只需找到一種3點(diǎn)著色,如圖1,c((11))=c({2,3})=1,c((22))=c({1,3})=2,c((33))=c({1,2})=3;顯然這種著色一定是(3,2)-條件著色.
(iii) 當(dāng)r=3時(shí),根據(jù)性質(zhì)1-(ii),χ3(Sn)4:
按引理3著色已經(jīng)是4點(diǎn)著色,條件C1顯然滿足,下面證條件C2成立.
因圖Sn極點(diǎn)是2度點(diǎn),與其關(guān)聯(lián)的頂點(diǎn)都取了不同的顏色;下面考慮任意度數(shù)大于3的頂點(diǎn)(即度數(shù)等于4)的鄰點(diǎn)至少有3種顏色,在圖S2中,{1,2},{1,3},{2,3}三頂點(diǎn)互為鄰點(diǎn),且都與極點(diǎn)相連,故這三點(diǎn)的鄰點(diǎn)著色數(shù)等于3.圖Sn是由數(shù)個(gè)S2組成的,只需考慮在圖S2中是極點(diǎn)在圖Sn中不是極點(diǎn)的點(diǎn)的鄰集色數(shù).即圖S3中形如{12}這樣的點(diǎn),如圖3,顯然此點(diǎn)的鄰集色數(shù)也是3.所以引理3的著色為(4,3)-條件著色.故當(dāng)r=3時(shí),χ3(Sn)=4.
(iv) 當(dāng)r4時(shí),根據(jù)性質(zhì)1-(i),χr(Sn)=χ4(Sn).只需考慮r=4時(shí)的條件著色.
根據(jù)性質(zhì)1-(ii),χ4(Sn)5.
當(dāng)n=2時(shí),圖S2中(11),(22),(33),{1,2},{1,3},{2,3}六個(gè)頂點(diǎn)中,{1,2}與除了(33)的四個(gè)頂點(diǎn)相鄰,圖S2中除了(33)的五個(gè)頂點(diǎn)取不同的顏色:(11),(22)是{1,2}的兩個(gè)相鄰的頂點(diǎn),故不能取相同的顏色,同理(11),(22),(33)都不能取相同的顏色,(33)與{1,3},{2,3}相鄰,故不能取這兩頂點(diǎn)顏色,又因(33)與{1,2}是{2,3}的鄰點(diǎn),也不能取{1,2}的顏色,所以(33)不能取與其他五個(gè)頂點(diǎn)相同顏色,也就是當(dāng)圖S2中六個(gè)頂點(diǎn)中都取不同的顏色時(shí),此著色記為(6,4)-條件著色,又因6是可能的最小值,故χ4(S2)=6(如圖4).
由性質(zhì)1-(iv),χ4(Sn)χ4(S2)=6.
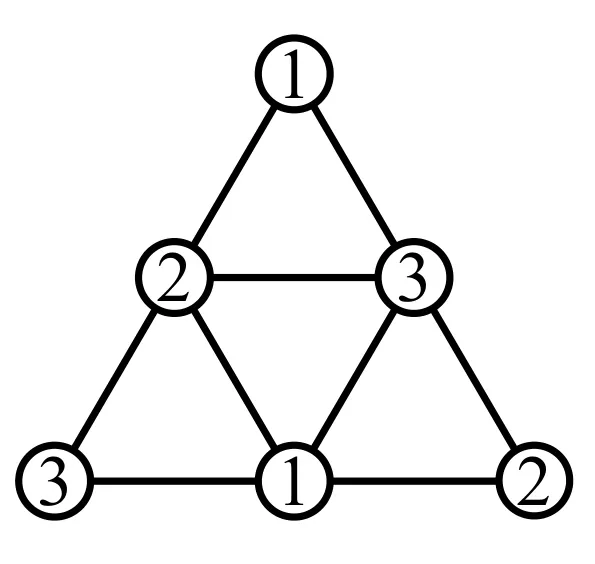
圖1 χ2(S2)=3
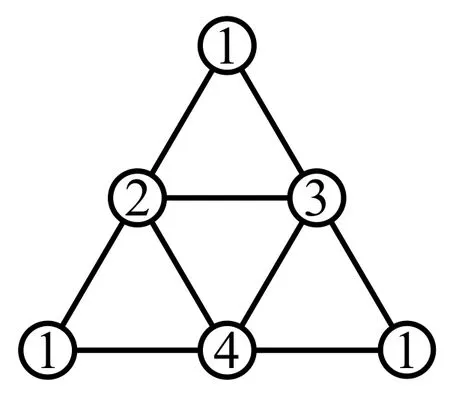
圖2 χ3(S2)=4
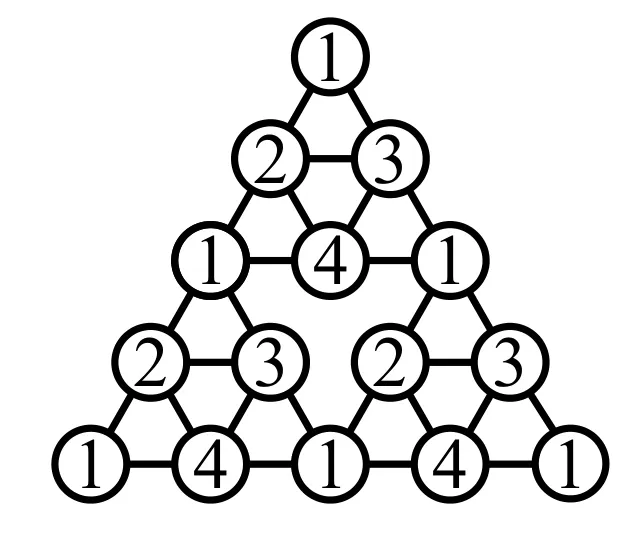
圖3 χ3(S3)=4
當(dāng)n=3時(shí),令c((111))=1;c((222))=2;c((333))=6;c({1,2})=3;c({1,3})=5;c({2,3})=4;則(S2)i的極點(diǎn)都取不同的顏色,故內(nèi)部點(diǎn)可由其余三種顏色著色.故S3可由S2的六種顏色著色.
設(shè)c是圖Sn的一個(gè)r=4的條件著色,c(i···i)=x,(i∈{1,2,3};x∈{1,2,3,4,5,6}),這里x是極點(diǎn)(i···i)的顏色.
下面證明:當(dāng)n是偶數(shù)時(shí),存在一個(gè)條件著色c使得c(1···1)=1,c(2···2)=3,c(3···3)=5;當(dāng)n是奇數(shù)時(shí),存在一個(gè)條件著色c使得c(1···1)=1,c(2···2)=2,c(3···3)=6.
當(dāng)n=2,3時(shí),如圖4,5,顯然存在.
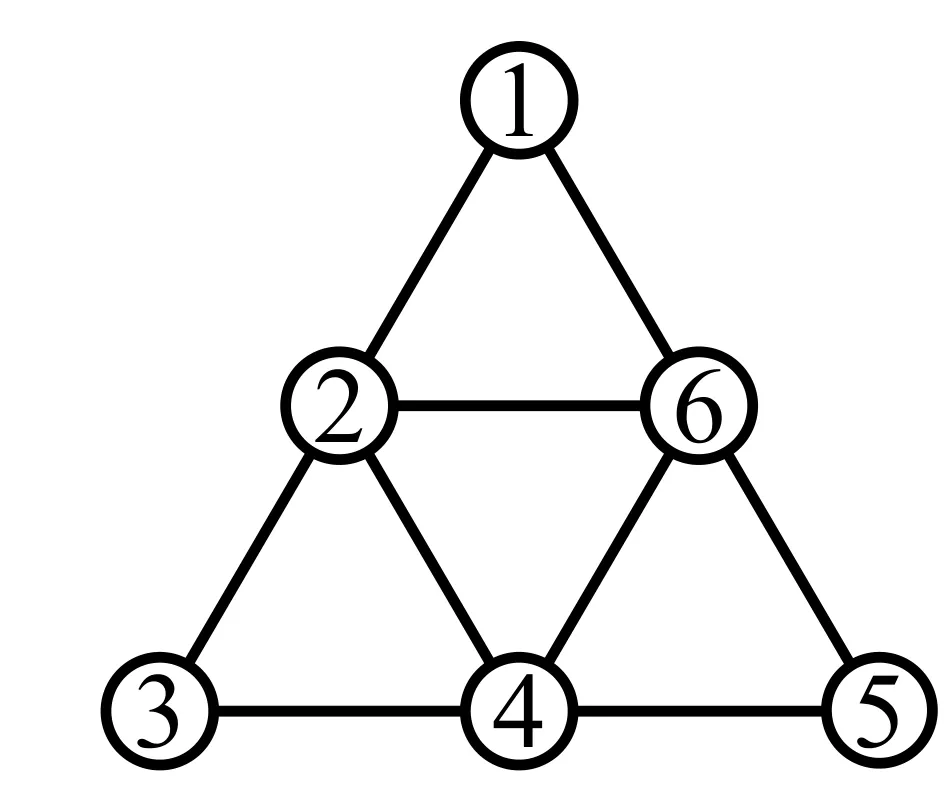
圖4 χ4(S2)=6
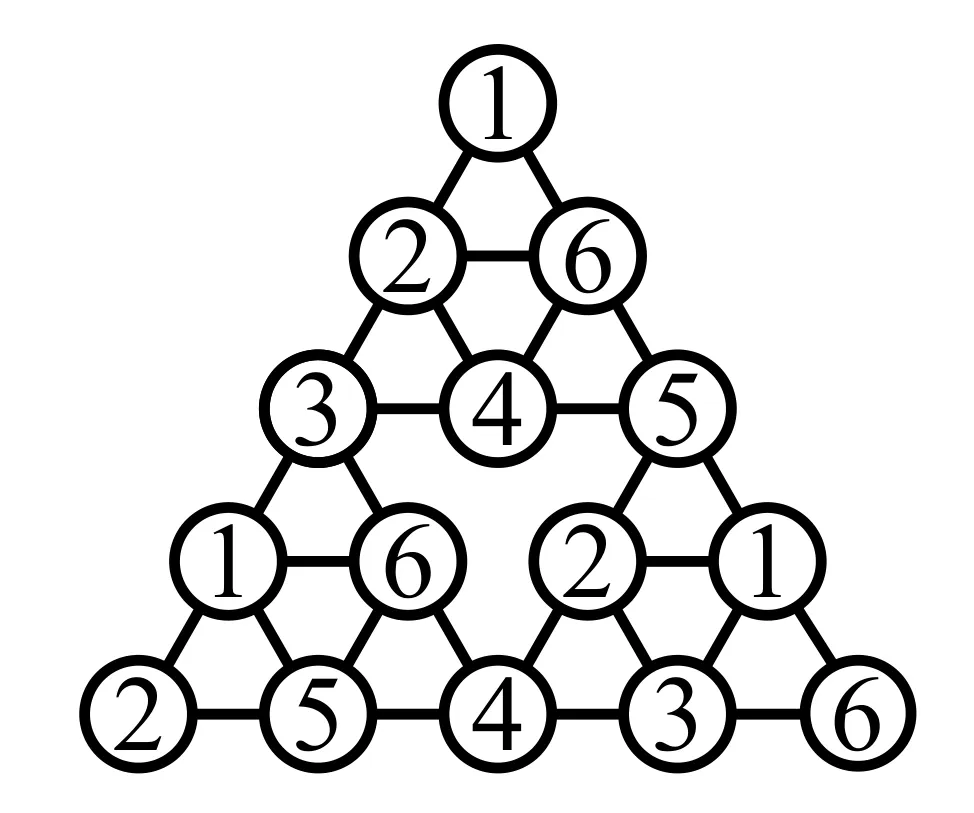
圖5 χ4(S3)=6
當(dāng)n是偶數(shù)時(shí),Sn+1的著色如下:是Sn+1,1的著色,使得是的著色,使得綜上,
當(dāng)n是奇數(shù)時(shí),Sn+1的著色如下:是Sn+1,1的著色,使得是Sn+1,2的著色,使得是Sn+1,3的著色,使得綜上,
故Sn可由S2的六種顏色著色.
所以,當(dāng)r4時(shí),故χr(Sn)=6.
定理2若n≥2,r≥1,則
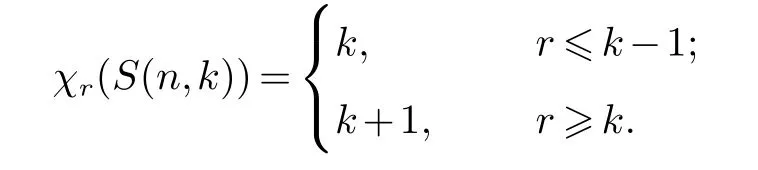
證明由S(1,k)=Kk,S(1,k)?S(n,k),又由性質(zhì)1-(iii)(iv),則有
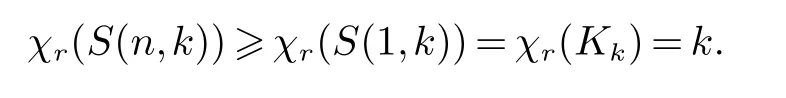
(i) 當(dāng)rk?1時(shí),設(shè)c是圖S(n,k)一個(gè)著色,對(duì)?(u1···un)∈S(n,k),令c((u1···un))=un;
下面證明:當(dāng)rk?1時(shí),圖S(n,k)取該著色即為(k,r)-條件著色.
(a) 先證是正常著色,即條件C1:
圖S(n,k)包含兩類邊,即?uv∈E(S(n,k)),
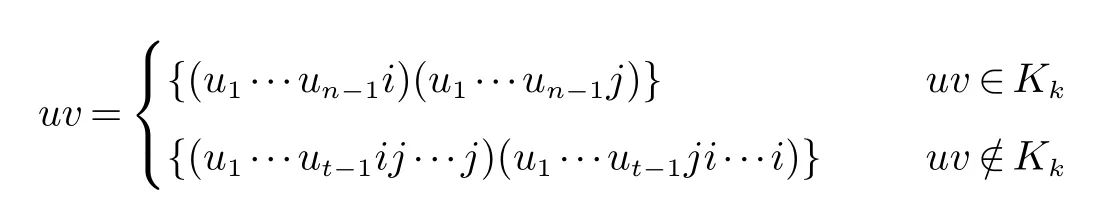
其中uk,i,j∈{1,2,···,k}.
當(dāng)邊在Kk中時(shí),令c((u1···un?1i))=i,c((u1···un?1j))=j.
當(dāng)邊不在Kk中時(shí),令c((u1···ut?1ij···j))=j,c((u1···ut?1ji···i))=i.
顯然此著色是正常著色.
(b) 再證條件C2.因任意點(diǎn)v都在Kk中,Kk中的點(diǎn)取不同的顏色,v的鄰點(diǎn)至少有k?1種顏色,故:|c(N(v))|k?1r,故(b)成立.
綜合(a)(b),當(dāng)rk?1時(shí),圖S(n,k)取上著色時(shí)為(k,r)-條件著色.又因k是滿足條件最小的著色,故χr(S(n,k))=k.
(ii) 當(dāng)rk時(shí),因r?,若要條件著色,只需將圖S(n,k)的每個(gè)頂點(diǎn)的鄰點(diǎn)都取不同的顏色.即
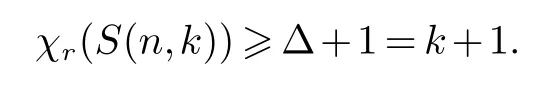
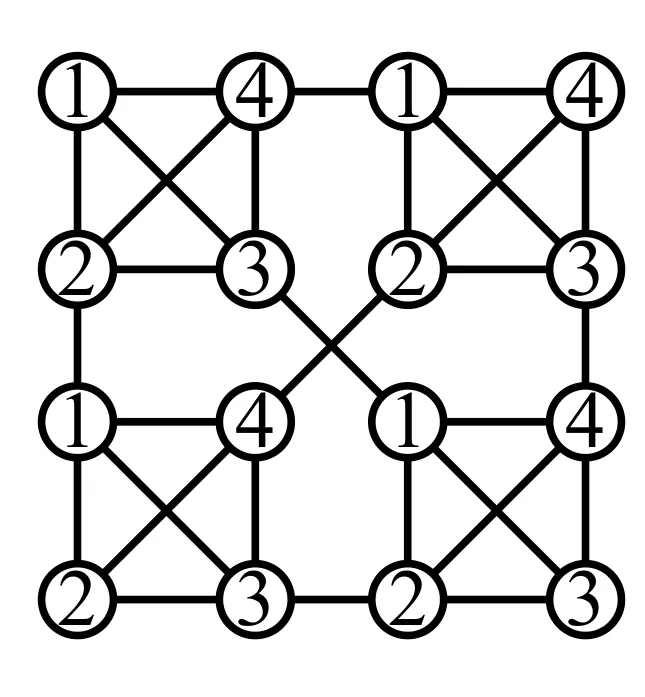
圖6 χr(S(2,4))=4,r3
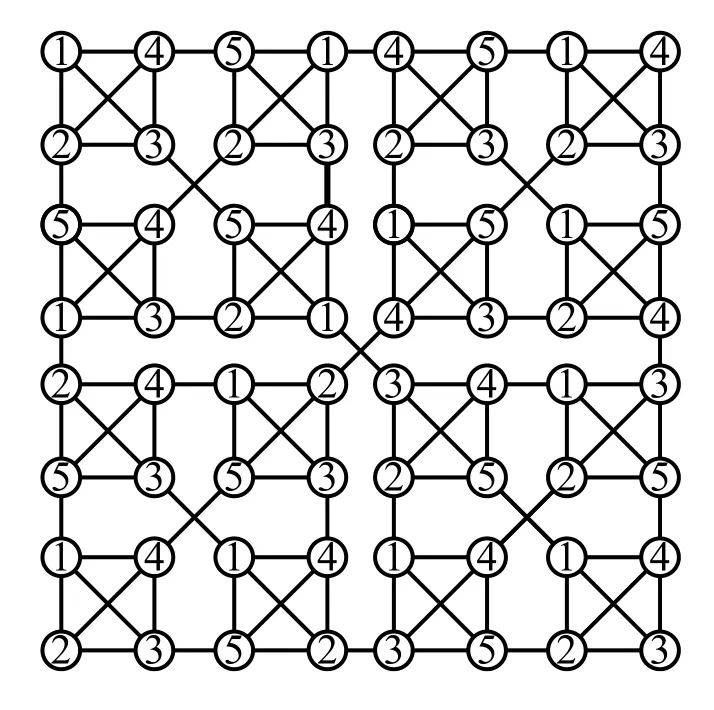
圖7 χr(S(3,4))=5,r4
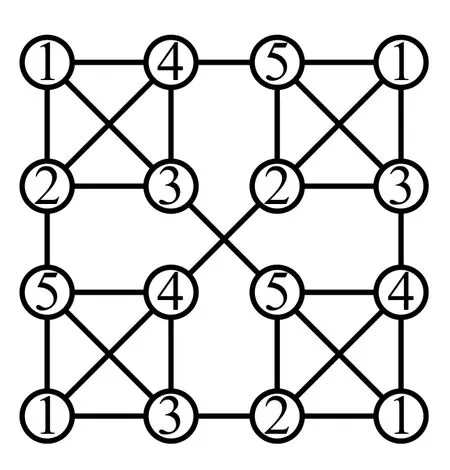
圖8 χr(S(2,4))=5,r4
下面證明:圖S(n,k)存在一個(gè)(k+1,r)-條件著色c.令
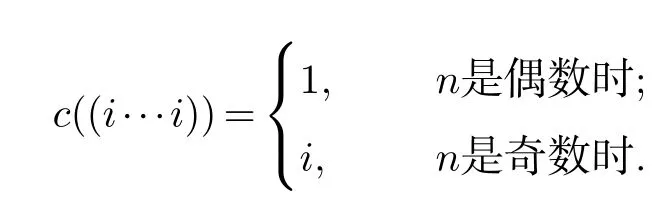
當(dāng)n=2,對(duì)圖S(2,k)進(jìn)行著色,令c((ii))=1,c((h1))=k+1,c((ij))=j其中i∈{1,2,···k},h∈{1,2,···k}/{1},j∈{1,2,···k}/{1,i},則每個(gè)頂點(diǎn)的鄰點(diǎn)的顏色都不同,即著色為(k+1,r)-條件著色.故χr(S(2,k))=k+1.
當(dāng)n=3時(shí),對(duì)圖S(3,k)i,將圖S(2,k)色數(shù)通過(guò)1→i,k+1→1,i→k+1(1)變換后,分別給圖S(3,k)i進(jìn)行此著色.則有c((iii))=c((ijj))=i,c((ijj))(),又c((jii))=j,圖S(3,k)的所有點(diǎn)的鄰點(diǎn)都取不同的顏色,故此著色都為(k+1,r)-條件著色.
當(dāng)n是偶數(shù)時(shí),假設(shè)在圖S(n,k)中,令c((i···i))=1,c((h1···1))=k+1,c((ij···j))=j;i∈{1,2,···k},h∈{1,2,···k}/{1},j∈{1,2,···k}/{1,i}時(shí),內(nèi)部可(k+1,r)-條件著色.在圖S(n+1,k)i中,將S(n,k)色數(shù)通過(guò)1→i,k+1→1,i→k+1(1)變換后,分別給圖S(n,k)i進(jìn)行此著色,則有c((i···i))=c((ij···j))=i(1,i}),c((ji···i))=j,故圖S(n+1,k)存在(k+1,r)-條件著色.
當(dāng)n是奇數(shù)時(shí),假設(shè)在圖S(n,k)中,令c((i···i))=c((ij···j))=i(j1,i}),若內(nèi)部可(k+1,r)-條件著色.在圖S(n+1,k)i中,將S(n,k)色數(shù)通過(guò)i→1,1→k+1,k+1→i(1)變換后,分別給圖S(n+1,k)i進(jìn)行此著色,則有c((i···i))=1,c((h1···1))=k+1,c((ij···j))=j,c((ji···i))=i;i∈{1,2,···,k},h∈{1,2,···k}/{1},j∈{1,2,···k}/{1,i},故圖S(n+1,k)存在(k+1,r)-條件著色.
由此方法,圖S(2,k)的(k+1,r)-條件著色可以推得圖S(3,k)的(k+1,r)-條件著色,依次類推可以得到圖S(n,k)的(k+1,r)-條件著色.
綜上,當(dāng)rk時(shí),χr(S(n,k))=k+1.

