Jian-hua WU (吳建華), Zhun XU (許準), Li YAO (姚莉), Fei MA (馬飛)

?

Ski-jump trajectory based on take-off velocity*

Jian-hua WU (吳建華)1, Zhun XU (許準)1, Li YAO (姚莉)2, Fei MA (馬飛)1

1. College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China, E-mail: jhwu@hhu.edu.cn 2. College of Water Conservancy and Ecological Engineering, Nanchang Institute of Technology, Nanchang 330099, China (Received December 10, 2015, Revised January 18, 2016)

The theoretical method estimating ski-jump trajectory was paid attention to and modified. The present method is based on the effects of the take-off velocity and the angle in the sensitivity analysis of parameters. The experiments are conducted for a triangular-shaped flip bucket in order to reveal the relationships between the take-off velocity and its influencing factors. The results show that, the take-off velocity has a much larger effect on the impact point than the take-off angle. The take-off velocities of both upper and lower trajectories are all functions of the approach flow Froude number, the deflector height and the deflection angle, especially, the results of the deflection angle ofcould be directly used when this angle is larger than. Meanwhile, this method is checked and the maximum relative errors of bothandare 5.1% and 5.6%, respectively.

trajectory, triangular-shaped flip bucket, take-off velocity, sensitivity analysis of parameters

In the designs for the ski-jump type energy dissi- pation, the theory of the projectile for a rigid body is often used to estimate the jet trajectory[1]. This theory involves two basic hypotheses in the estimation of the trajectory. One is that the water is a rigid body, and the other is that the air resistance can be neglected. Thus, in certain engineering projects, a deviation about 20%-60% is often found if the theory of the pro- jectile for a rigid body is directly applied[2].

The sources of errors of the theoretical method include the effects of the air resistance, the difference between the take-off angle of the upper or lower traje- ctory and the deflection angle, and the changes of the take-off velocity of the upper or lower trajectory with the approach flow velocity. Much effort was made to improve the methodology of estimating the trajectory.

For the effect of the air resistance, Liu et al., based on a theoretical analysis, proposed an air resis- tance coefficient for modifying the estimation of the trajectory, but this coefficient involves some factors, such as the densities of both the air and jet flows, the resistance, and an unknown function of the take-off angle, so this cannot be conveniently used due to some unknown variables[3]. Further, for circular-sha- ped flip buckets, Wu et al. proposed expressions of the air resistance coefficient of the upper and lower traje- ctories, which could be used directly in the estimatio- ns of the trajectory[4].

With respect to the difference between the take- off and deflection angles, Steiner et al.[5]and Heller et al.[6]observed that the take-off angle of upper or lower trajectory is clearly smaller than the deflection angle of the flip bucket, and deemed that the decrease of the take-off angle is related to the relative deflector height and the approach flow Froude number for a triangular- shaped flip bucket, while it is related to the relative flow depth for a circular flip bucket. Earlier, Wu and Ruan[7]presented an improved method for calculating the lower take-off angle with consideration of the transverse fluctuating velocity and the flow depth for the aerator device with a ramp.

The trajectory of a mass point can be expressed in cases without air resistance (Fig.1) as

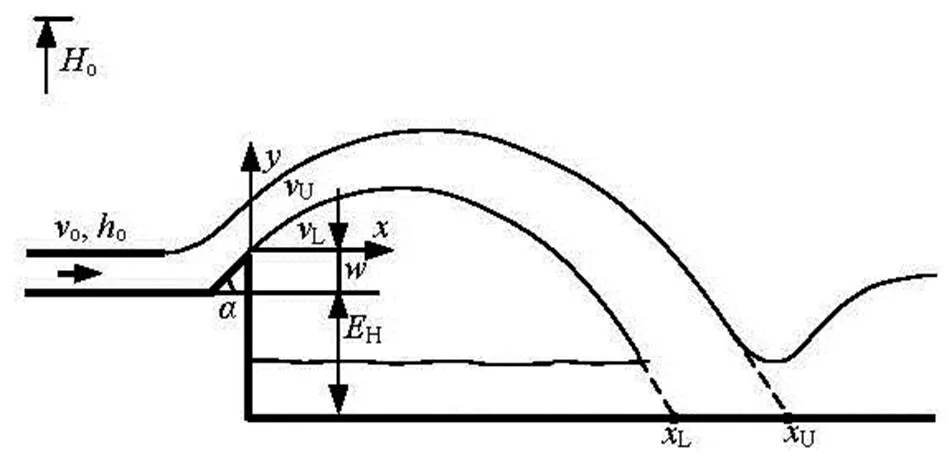
Fig.1 Definition of plane ski-jump

From Eq.(1), the impact point is dominated by,and. For a given project, however,keeps constant. According to the recent investigation, there is the difference between the take-off and deflection angles for the upper or lower trajectory[5,6]. If the effe- ct of the angle difference on the jet trajectory is small and then it could be neglected, the impact point could be conveniently estimated by means of Eq.(1) with suitable estimations of the upper or lower take-off ve- locity.

The objectives of this paper are to theoretically determine the effects of the take-off velocity or the de- flection angle on the trajectory through a sensitivity analysis method under the condition of constant, to give a take-off velocity expression of the upper or lower trajectory, and to check the error range and re- liability of the present estimation method for the traje- ctory.

With Eq.(1) giving the relation between the im- pact pointand the take-off velocity (or) or the deflection angle, the sensitivity functionsandabout the take-off velocity and the deflection angle could be written as[8]

respectively. And

Calculations demonstrate thatis between 1.09 and 1.93, andis between 0.02 and 0.21, when0–40 m/s and0o–45oon the basis of Eqs.(2)-(5). Clearly, the minimumis much larger thanin the present range. It means that the difference between the take-off and deflection angles could be neglected in the estimation of the trajectory due to the smaller effect of the angle than that of the velocity. With this knowledge, we could directly estimate the impact point of the ski-jump when the take-off velocity of the upper or lower trajectory is obtained.

Table 1 lists the cases and geometric parameters of the models. The cases are divided into two sets. Cases M12-M32 are used to study the effects of, while cases M21-M23 are for the effects of. In the experiments, the triangular-shaped flip bucket models were designed, with0.50 m (Fig.1). The maxi- mum1.50 m, and1.56-3.60.

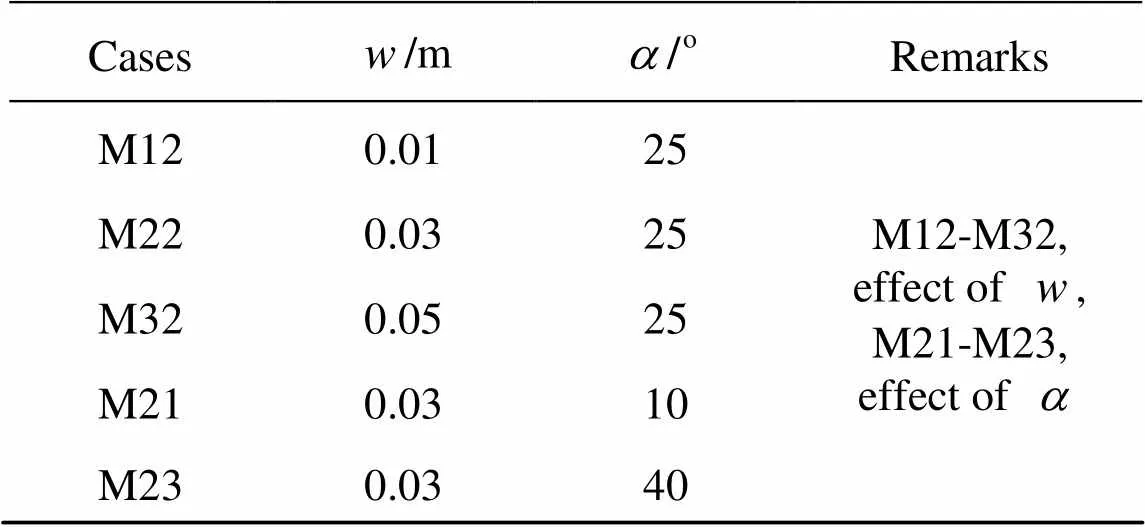
Table 1 Cases and geometric parameters of models

By means of the dimensional analysis, the relati- ve take-off velocity can be given by

For the upper or lower jet trajectory,could be re- placed byor.

Figure 2 shows the variations ofwithat differentand. Obviously,is in a good linear relationship with, and increases with the increasing. In order to further reveal the effect of, Fig.3 is obtained by means of parameter fitting.

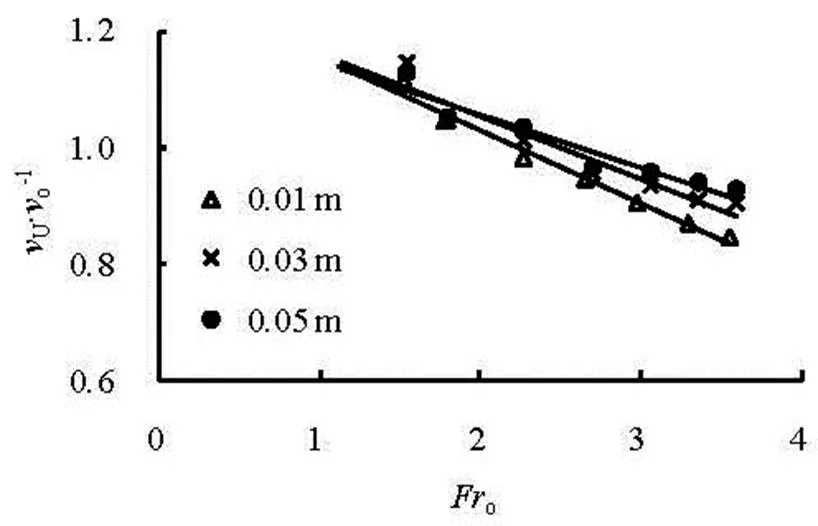
Fig.2 Variations of with at different w and

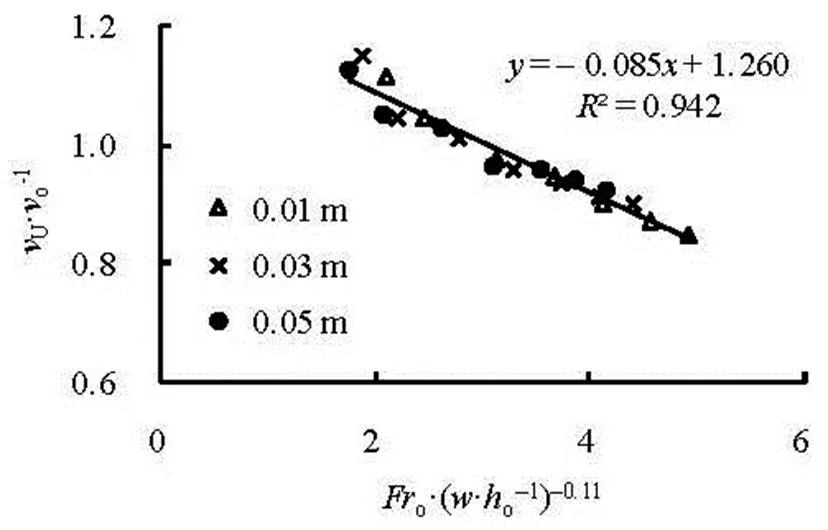
Fig.3 Variations of with at

Figure 4 shows the variations ofwithat differentand.is still well linear with, and decreases with the increasing. Meanwhile, a special phenomenon should be noticed, i.e., the values ofare very close atand. It may imply that, where the effect ofonis concerned, there exists an influencing range of. For the deflection angle larger than 25°, the variations ofwithcould directly use the results of.

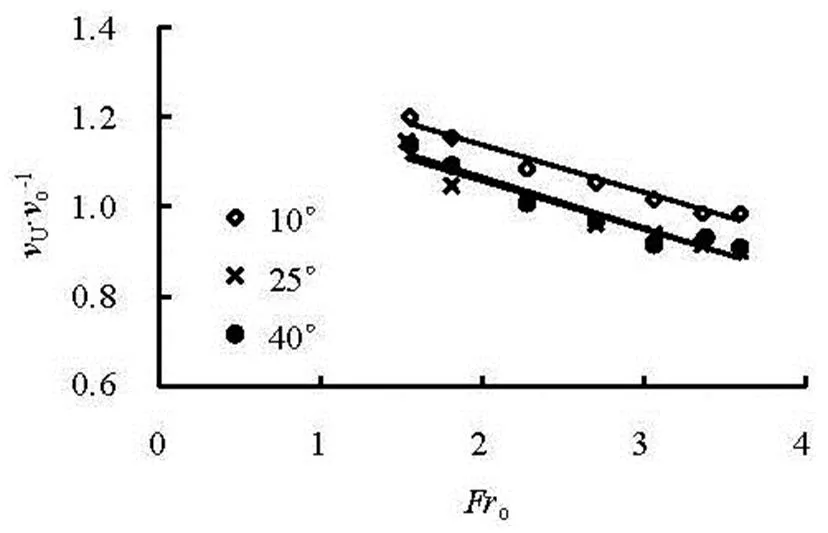
Fig.4 Variations of with at different and

Figure 5 gives the relationship betweenand its influencing factors, and the best fit is (0.945)

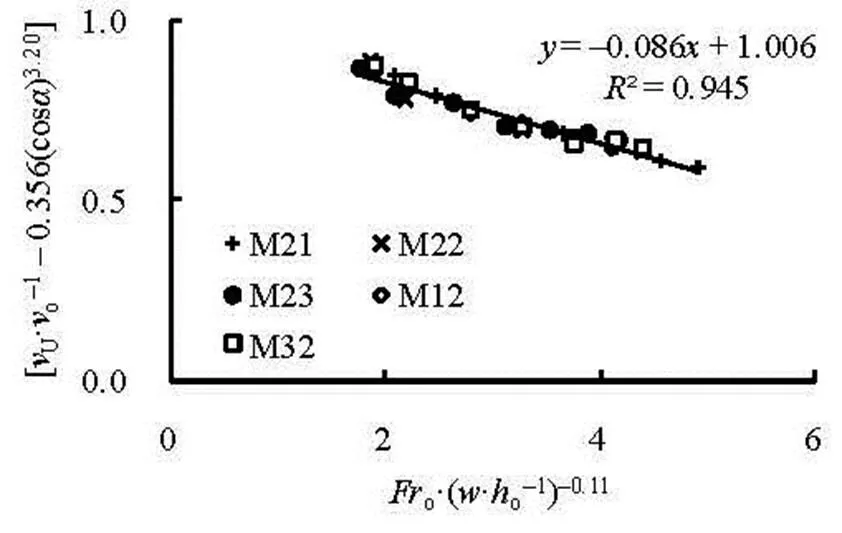
Fig.5 Relationship between and

Similar to the upper take-off velocity, we have, on the basis of the data of Fig.6,

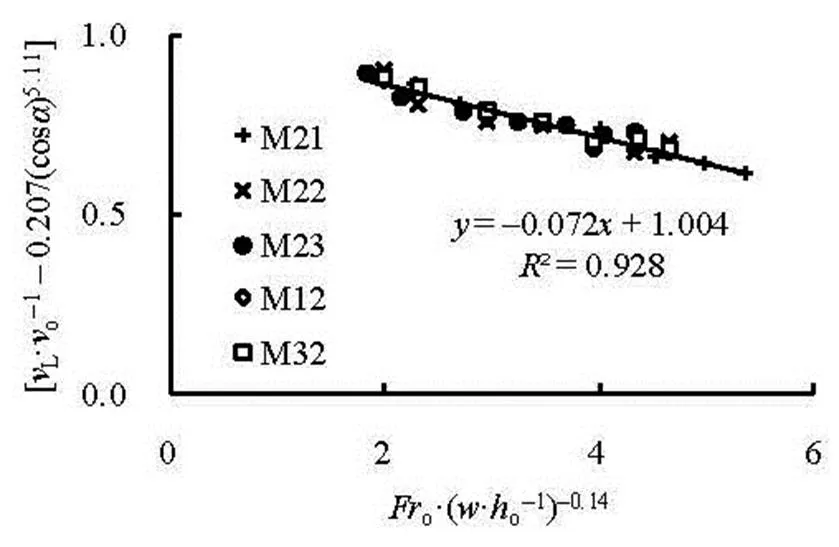
Fig.6 Relationship between and

Figures 7 and 8 show comparisons between the calculated (subscript cal.) and experimental (subscript exp.) impact points of both upperUand lowerLtrajectories, respectively. For the calculations ofUcalandLcalaccording to Eq.(1), bothUandLcould be obtained on the basis of Eqs.(7) and (8). In those two figures, the dotted lines show the range of the relative error () of 10% on the basis of

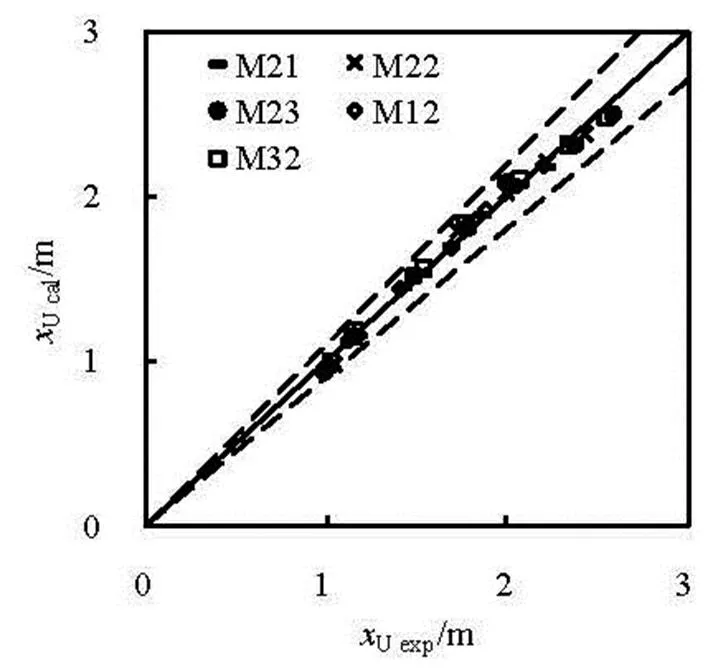
Fig.7 Comparison between and

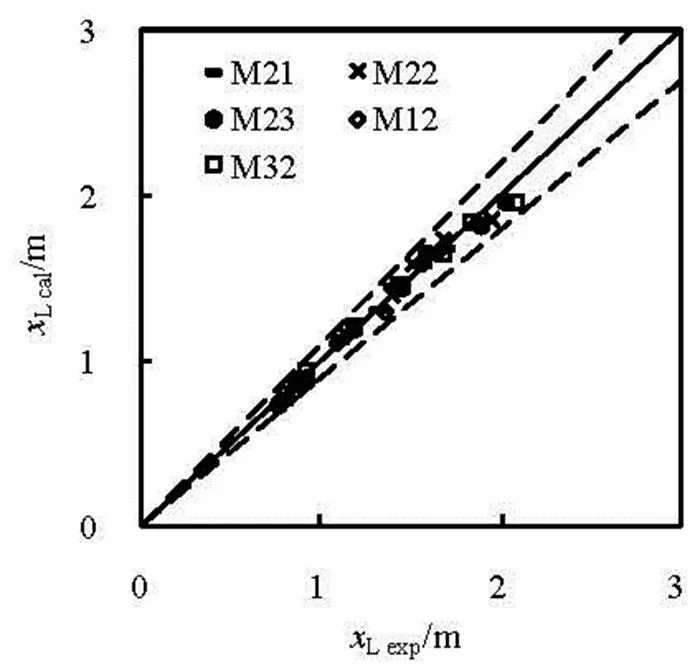
Fig.8 Comparison between and

It could be seen that, the maximum relative errors ofandare 5.1% and 5.6%, respectively.

In short, the sensitivity analysis of parameters indicates that the take-off velocity has a much larger effect on the impact point than the take-off angle. In this regard, a method estimating the trajectory is presented if the take-off velocity can be obtained.

For the triangular-shaped flip bucket, the take-off velocities of both upper and lower trajectories are all functions of the approach flow Froude number, the de- flector height and the deflection angle, especially, the results of deflection angle ofcould be directly used when this angle is larger thanand less than.

Compared with the experimental data, the maxi- mum relative errors of bothandare 5.1% and 5.6%, respectively, when using the methodology in this paper.

References

[1] DL/T5166-2002. Design specification for river-bank spillway[S]. The State Economy and Trade Commission, China, 2002(in Chinese).

[2] LI Chong-zhi. Free jet of high velocity flow over the bu- cket[J]. Journal of Hydraulic Engineering, 1963, (2): 25-32(in Chinese).

[3] LIU Xuan-lie, ZHANG Wen-zhao. Effect of air resistance to a trajectory jet[J]. Journal of Tianjin University, 1982, 108(2): 67-77(in Chinese).

[4] WU Jian-hua, ZHANG Xiao-yan and MA Fei et al. Ski jump trajectory with consideration of air resistance[J]. Journal of Hydrodynamics, 2015, 27(3): 465-468.

[5] STEINER R., HELLER V. and HAGER W. H. et al. De- flector ski jump hydraulics[J]. Journal of Hydraulic En- gineering, ASCE, 2008, 134(5): 562-571.

[6] HELLER V., HAGER W. H. and MINOR H.-E. Ski jump hydraulics[J]. Journal of Hydraulic Engineering, ASCE, 2005, 131(5): 347-355.

[7] WU Jian-hua, RUAN Shi-ping. Cavity length below chute aerators[J]. Science in China Series E: Technological Sciences, 2008, 51(2): 170-178.

[8] ZHANG Guang, ZHU Wei-shen. Parameter sensitivity analysis and optimizing for test programs[J]. Rock and Soil Mechanics, 1993, 14(1): 51-58(in Chinese).

10.1016/S1001-6058(16)60618-2 2016,28(1):166-169