安徽省臨泉縣第一中學(xué)(236400) 曹勝龍

橢圓外切四邊形的一個(gè)幾何恒等式

安徽省臨泉縣第一中學(xué)(236400) 曹勝龍

文[1]給出了三角形內(nèi)切橢圓的一個(gè)如下幾何恒等式:

命題1設(shè)△ABC的一個(gè)內(nèi)切橢圓分別與BC,CA,AB邊切于D,E,F,則下列等式恒成立

筆者讀后受到啟發(fā)進(jìn)而思考,這個(gè)結(jié)論既然在三角形中成立,而在平面幾何中,三角形是最基本、最簡(jiǎn)單的多邊形,如果將三角形的邊數(shù)進(jìn)行拓展四邊形,結(jié)論是否還會(huì)成立?按照馬老師的探索思路,發(fā)現(xiàn)這個(gè)幾何恒等式對(duì)四邊形也是成立的,故而得到如下結(jié)果:

命題2 設(shè)橢圓外切四邊形ABCD的邊DA,AB,BC,CD與橢圓切于E,F,G,H,則下列等式恒成立

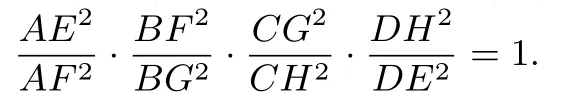
證明如圖所示,設(shè)P,Q是橢圓的兩個(gè)焦點(diǎn),P關(guān)于AD,AB的對(duì)稱點(diǎn)分別是M,N,由橢圓的光學(xué)性質(zhì)知M,N兩點(diǎn)必落在直線EQ,FQ上且MQ=NQ=2a(橢圓的長(zhǎng)軸長(zhǎng)).又由于AM=AN=AP,所以△AMQ∽△ANQ,因此∠AMQ=∠ANQ,設(shè)∠AEP=α,∠AFP=β,則在△AME中,由正弦定理得

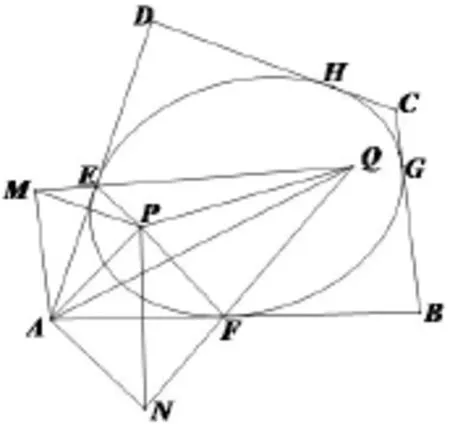
圖1

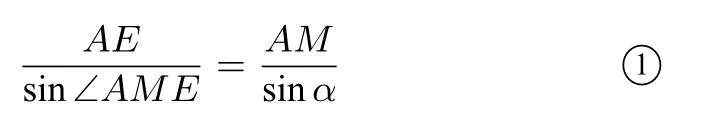
同理在△ANF中

由AM=AN=AP,∠AMQ=∠ANQ,并結(jié)合①②得

在△EPQ中由余弦定理得

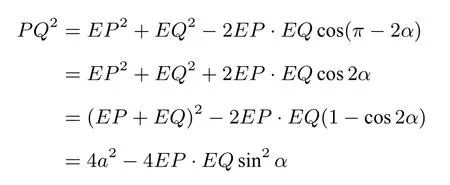
所以b2=EP·EQsin2α同理,在△FPQ中,b2=FP· FQsin2β.所以

按此思路,繼續(xù)擴(kuò)大邊數(shù),我們可得橢圓外切n邊形A1,A2,...,An也有此恒等式

可類比猜想得

[1]馬利國(guó).三角形內(nèi)切橢圓的又一個(gè)幾何恒等式[J].中學(xué)數(shù)學(xué)教學(xué)參考,2011,4.

[2]周峻民.三角形內(nèi)切橢圓的一個(gè)幾何恒等式[J].數(shù)學(xué)通報(bào),2010,8.