耿杰, 宋衛(wèi)東

(1.安徽信息工程學(xué)院,安徽 蕪湖 241000;2.安徽師范大學(xué)數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽 蕪湖 241000)

一些球?qū)ΨQ射影平坦的Finsler度量的構(gòu)造

耿杰1, 宋衛(wèi)東2

(1.安徽信息工程學(xué)院,安徽 蕪湖 241000;2.安徽師范大學(xué)數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽 蕪湖 241000)

研究刻畫球?qū)ΨQFinsler度量的射影平坦性質(zhì)的偏微分方程,通過(guò)對(duì)射影平坦Finsler度量PDE的研究,構(gòu)造了兩類球?qū)ΨQ射影平坦Finsler度量,得到了一些球?qū)ΨQ的射影平坦Finsler度量,并進(jìn)一步給出這些Finsler度量的射影因子和旗曲率.

球?qū)ΨQ;射影平坦;旗曲率;Finsler度量

1 引言及主要結(jié)論

由于有著廣泛的應(yīng)用背景,Finsler幾何越來(lái)越引起人們的關(guān)注[1?7],并取得了許多重要的成果.Finsler幾何中的一個(gè)基本問(wèn)題是研究在開(kāi)區(qū)域U?Rn中射影平坦的特征.Finsler度量在U上射影平坦是指其測(cè)地線為直線,這是Hilbert第四問(wèn)題的一般情形[1].1903年,Hamel[2]證明了Finsler度量F=F(x,y)在U上是局部射影平坦的充要條件為：Beltrami定理表明一個(gè)Riemann度量是局部射影平坦的當(dāng)且僅當(dāng)它具有常截面曲率.Finsler幾何中的旗曲率是Riemann幾何中截面曲率的自然拓廣.

設(shè)F=F(x,y)是具有Scalar旗曲率的射影平坦Finsler度量,那么旗曲率K是TU上的一個(gè) Scalar函數(shù),即

其中

表示射影因子[7].

如果Finsler度量F(x,y)是球?qū)ΨQ的當(dāng)且僅當(dāng)F(x,y)滿足

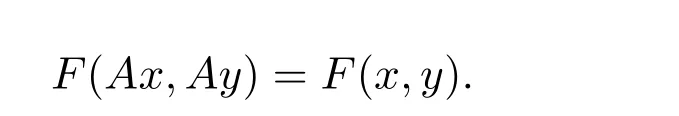
球?qū)ΨQFinsler度量是對(duì)Finsler度量的進(jìn)一步研究.而射影平坦Finsler度量也是對(duì)Finsler度量的特征的豐富.那么球?qū)ΨQ的Finsler度量與射影平坦的Finsler度量之間存在著什么樣的關(guān)系呢?對(duì)于這個(gè)問(wèn)題,我們有如下結(jié)論:

定理1.1[7]設(shè)

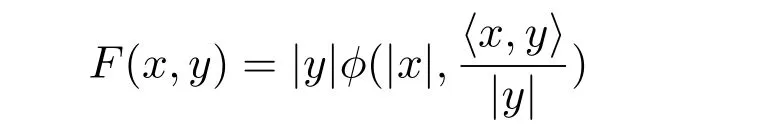
是Bn(r)上的球?qū)ΨQFinsler度量.則F=F(x,y)是射影平坦的當(dāng)且僅當(dāng)?=?(b,s)滿足

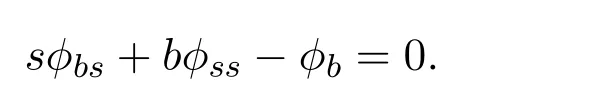
其中

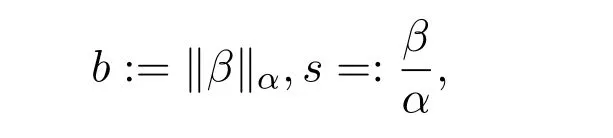
?b表示?對(duì)b一次偏導(dǎo).

本文通過(guò)對(duì)射影平坦Finsler度量PDE的研究,構(gòu)造了兩類球?qū)ΨQ射影平坦Finsler度量,并分別給出了這兩類球?qū)ΨQ射影平坦Finsler度量的射影因子和旗曲率.

定理1.2設(shè)

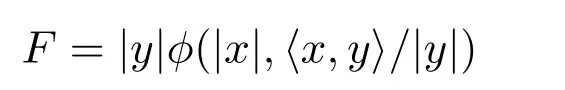
是在Bn(r)的球?qū)ΨQFinsler度量,若

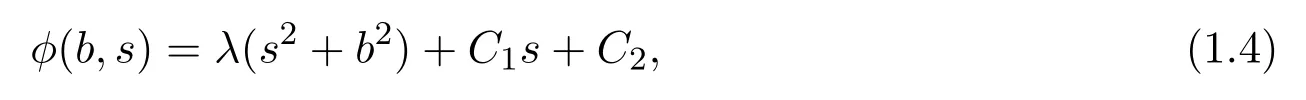
其中λ,C1,C2是任意常數(shù),那么以下結(jié)論成立:

(1)(1.4)式所給出的在Bn(r)上的球?qū)ΨQFinsler度量F是射影平坦的.它的射影因子P表示為

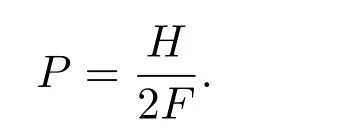
(2)該Finsler度量F具有Scalar曲率,它的旗曲率K 表示為

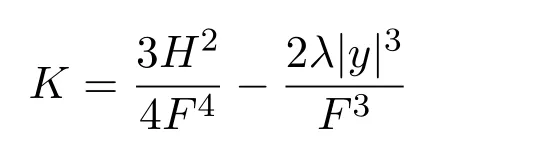
其中

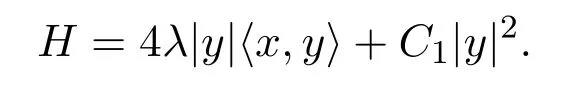
注1.1當(dāng)λ=0,C1=C2=1,

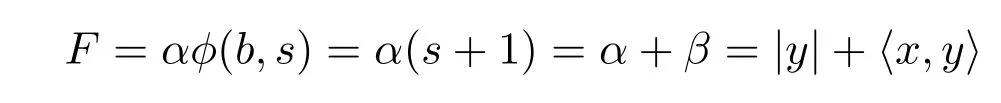
是Randers度量.它是球?qū)ΨQ射影平坦Finsler度量,它的射影因子P表示為

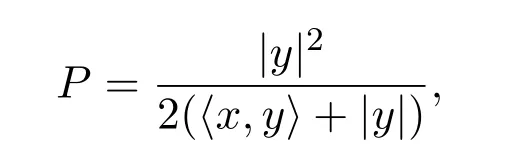
它的旗曲率K表示為

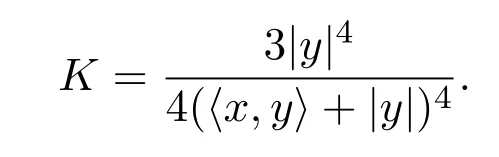
定理1.3設(shè)

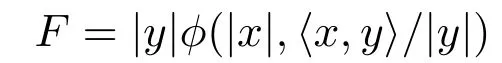
是在Bn(r)的球?qū)ΨQFinsler度量,若

其中C是任意常數(shù),那么以下結(jié)論成立:

(1)(1.2)所給出的在Bn(r)上的球?qū)ΨQFinsler度量F是射影平坦的.它的射影因子P表示為

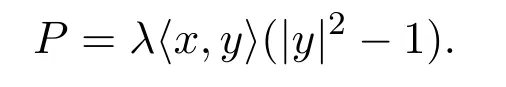
(2)該Finsler度量F具有Scalar曲率,它的旗曲率K 表示為

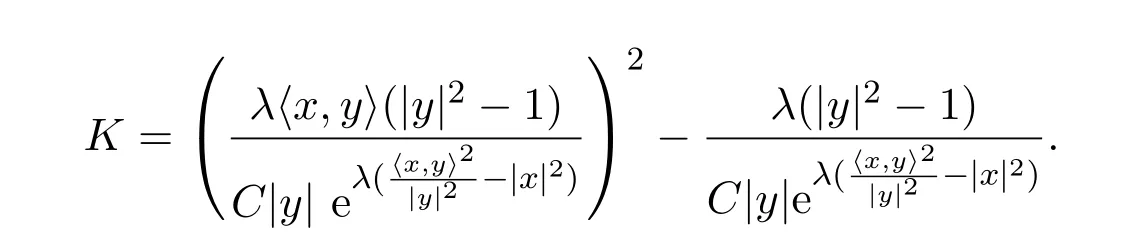
2 定理的證明

現(xiàn)在考慮下列PDE

的解.其中?=?(b,s).

2.1 定理 1.1的證明

若

將(2.2)代入(2.1)得到

其中 ”′”表示對(duì)x求一次偏導(dǎo).

由(2.3)得

其中λ是一個(gè)常數(shù).

(2.4)等價(jià)于

和

(2.5)的通解為

和(2.6)的通解可表示為

然后,聯(lián)立(2.7),(2.8),得到(2.1)的一個(gè)通解,

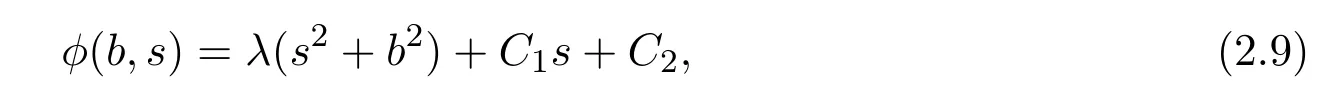
其中C1,C2都為任意的常數(shù).

2.2定理1.2的證明

再令

將(2.10)代入(2.1)我們得到

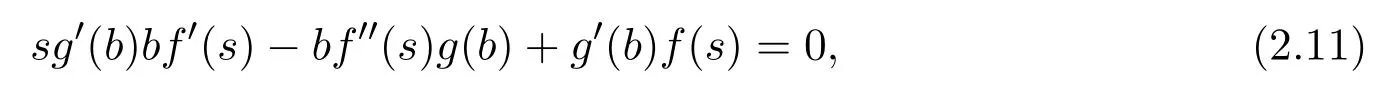
其中 ”′”表示對(duì)x求一次偏導(dǎo).對(duì)(2.11)進(jìn)行變形,得到

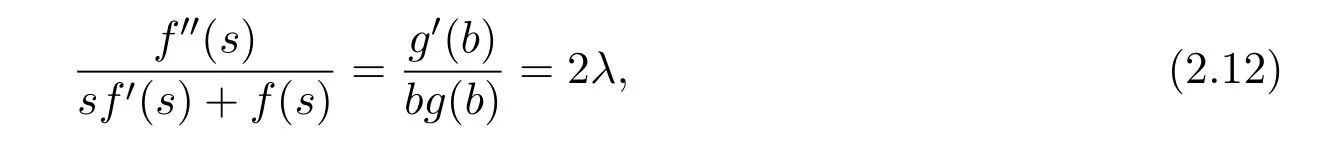
其中λ是一個(gè)常數(shù).

(2.12)等價(jià)于

和

(2.13)的通解可表示為

和(2.14)的通解為

由此,聯(lián)立(2.15),(2.16)可以得到(2.1)的另外一類通解,

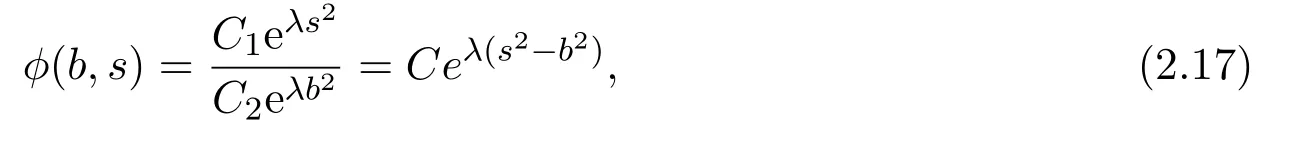
其中C1,C2,C 為任意常數(shù).

現(xiàn)在研究由 (2.9),(2.17)所確定的兩類射影平坦 Finsler度量,并求出它們射影因子和Scalar旗曲率.

首先來(lái)求由(2.9)所確定的射影平坦Finsler度量的射影因子和Scalar旗曲率.

設(shè)

所以,可得

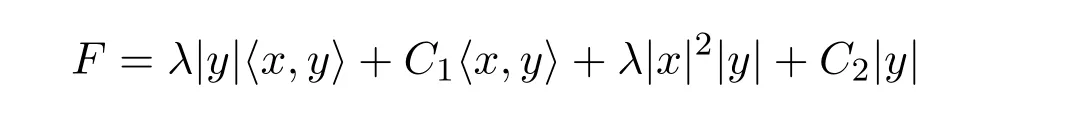
是一個(gè)球?qū)ΨQ射影平坦Finsler度量.

通過(guò)一個(gè)簡(jiǎn)單的計(jì)算,得出

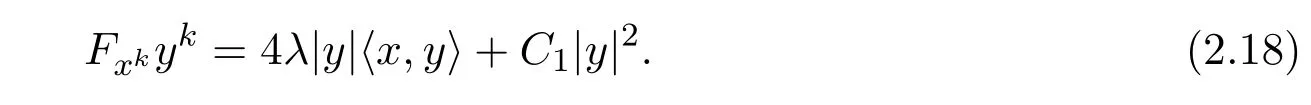
通過(guò) (3)知

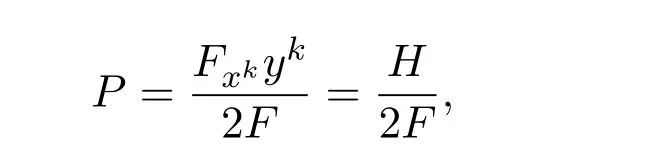
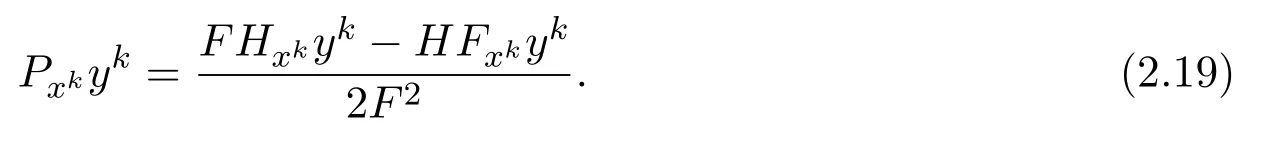
通過(guò)(2)得到

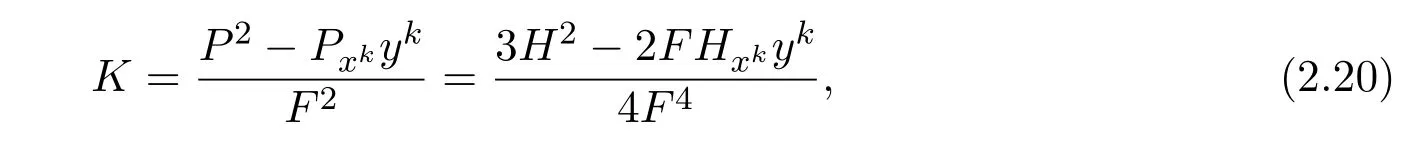
其中

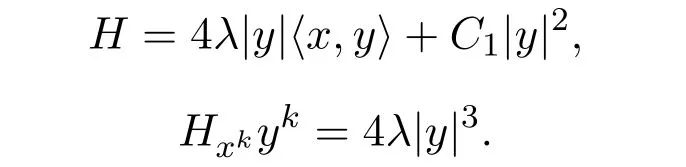
由(2.18),(2.19),(2.20)得出

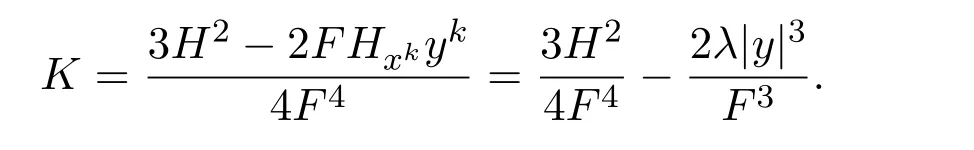
下面來(lái)求由(2.9)所確定的射影平坦Finsler度量的射影因子和Scalar旗曲率:

設(shè)

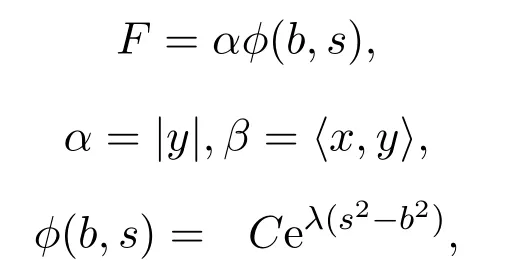
其中C是任意常數(shù).

所以,

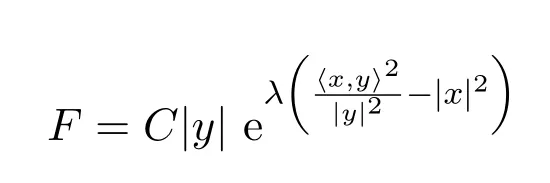
是一個(gè)球?qū)ΨQ射影平坦Finsler度量.

通過(guò)一個(gè)簡(jiǎn)單的計(jì)算,可得

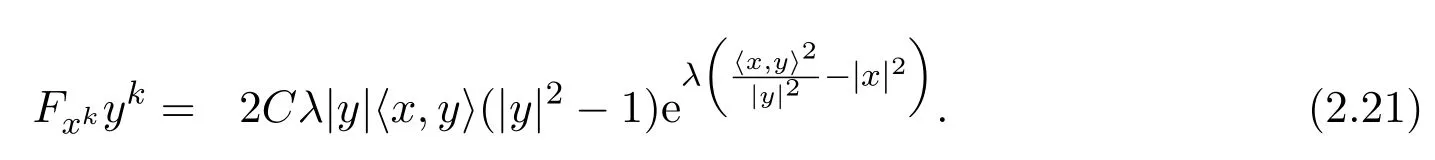
通過(guò) (3)有

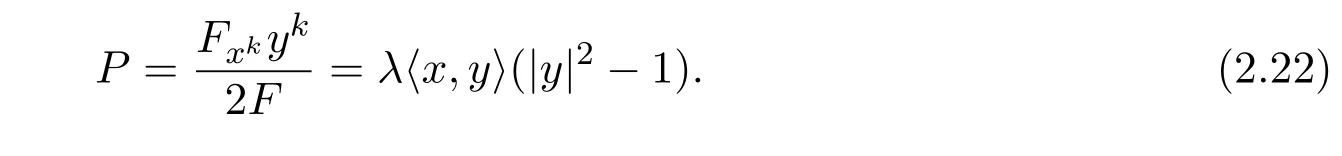
可得出

通過(guò) (2)知

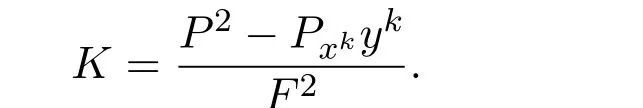
聯(lián)立(2.21),(2.22),(2.23)得到

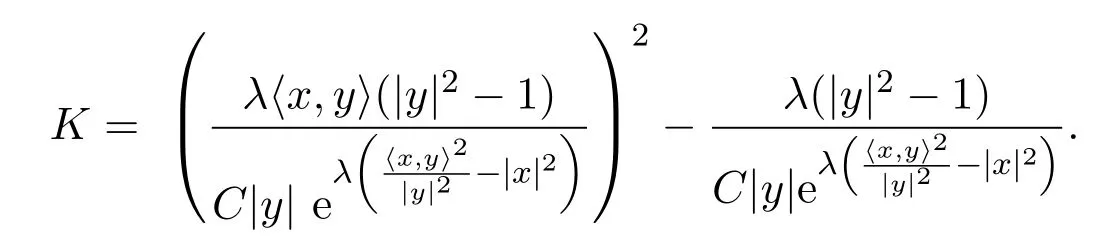
即得證.

[1]Hilbert D.Mathematical problems[J].Bull Amer Math.Soc.,2011,37:407-436.

[2]Shen Z.Projectively fl at Finsler metrics of constant fl ag curvature[J].Trans.Amer.Math.Soc.,2003,325:1713-1728.

[3]Hamel G.Uber die Geometrieen in denen die Geraden die Kürzesten sind[J].Mathematische Annalen,1931,104:672-699.

[4]Chern S S,Shen Z.Riemann-Finsler Geometry[M].Singapore:World Scienti fi c,2005.

[5]莫小歡.黎曼-芬斯勒幾何基礎(chǔ)[M].北京:北京大學(xué)出版社,2007.

[6]Cheng Y,Shen Z.Finsler Geometry[M].Beijing:Science Press,2012.

[7]Huang L,Mo H.A new class of projectively fl at Finsler metrics in terms of hypergeometrics functions[J].Publ.Math.Debrecen,2012,81:421-434.

Spherically symmetric Finsler metrics with scalar fl ag curvature

Geng Jie1,Song Weidong2
(1.Anhui Institute of Information Technology,Wuhu 241000,China;2.College of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China)

By investigating a PDE equivalent to these metrics being locally projectively fl at we create projectively fl at spherically symmetric Finsler metric in terms of error functions.Subsequently we obtain its projective factor and fl ag curvature.

quad spherically symmetric,projectively fl at, fl ag curvature,Finsler metric

O186

A

1008-5513(2017)05-0496-07

10.3969/j.issn.1008-5513.2017.05.007

2017-03-10.

國(guó)家自然科學(xué)基金(11071005);安徽省自然科學(xué)基金(KJ2017A795).

耿杰(1987-),碩士研究生,講師,研究方向：微分幾何.

宋衛(wèi)東(1958-),教授,研究方向:微分幾何.

2010 MSC:53C60,53A20