趙瑞通 梁瑞生 王發(fā)強(qiáng)

(華南師范大學(xué)信息光電子科技學(xué)院,廣東省微納光子功能材料與器件重點(diǎn)實(shí)驗(yàn)室,廣州 510006)(2017年3月4日收到;2017年8月20日收到修改稿)

1 引 言

量子糾纏在量子信息處理過程中的角色至關(guān)重要,尤其是在遠(yuǎn)距離量子通信過程中,量子糾纏經(jīng)常被用做量子通道連接遠(yuǎn)距離的兩個節(jié)點(diǎn).然而,在量子糾纏通道的分配設(shè)置過程中和通道建立后,糾纏不可避免地會受到通道和周圍環(huán)境噪聲的影響而降低,這就降低了遠(yuǎn)距離量子通信的保真度和安全性.為了獲得高品質(zhì)的量子糾纏通道來實(shí)現(xiàn)遠(yuǎn)距離量子通信,需要用到糾纏濃縮方案[1?4].糾纏濃縮就是從糾纏程度較低的部分糾纏態(tài)中提取出糾纏程度較高的糾纏態(tài)甚至是最大糾纏態(tài)的方法.1996年,第一個糾纏濃縮方案被提出[1],這個方案是利用Schmidt投影方法實(shí)現(xiàn)的,而且要求兩個參與者獲得部分糾纏態(tài)的系數(shù),也要用到聯(lián)合非破壞測量技術(shù).之后,人們提出了很多的糾纏態(tài)濃縮方法.文獻(xiàn)[5,6]分別利用線性光學(xué)元件發(fā)展了Schmidt投影方法.Bose等[7]提出了基于糾纏交換的糾纏濃縮,這種方法需要用到聯(lián)合Bell態(tài)測量.2008年,Sheng等提出了一個高效的糾纏濃縮方法,可以通過重復(fù)糾纏濃縮過程提高成功率[8],并在2012年將這個方案做了改進(jìn)[9].隨后,更多的糾纏濃縮方案相繼出現(xiàn),例如多粒子糾纏態(tài)濃縮,包括Greenberger-Horne-Zeilinger(GHZ)態(tài)[10,11],W態(tài)[12],團(tuán)簇態(tài)[13]等,以及多維度的超糾纏濃縮[14?16].

自從1998年Loss和DiVinoenz[17]提出在半導(dǎo)體量子點(diǎn)中利用電子自旋作為量子比特以來,自旋半導(dǎo)體量子點(diǎn)系統(tǒng)就由于其容易操作和擴(kuò)展,并且有較長的相干時間,成為最有希望實(shí)現(xiàn)量子計(jì)算機(jī)的方案之一.人們己經(jīng)提出了非常多的基于自旋半導(dǎo)體量子點(diǎn)來實(shí)現(xiàn)量子通信和量子計(jì)算的方案[18?23],量子點(diǎn)結(jié)構(gòu)還可以用作單光子源和糾纏光子源[24,25]等.Wang等[26]在2011年利用量子點(diǎn)和光學(xué)微腔的耦合系統(tǒng)構(gòu)建了電子自旋態(tài)的宇稱檢測門,并在此基礎(chǔ)上實(shí)現(xiàn)了自旋糾纏態(tài)的提純和濃縮.隨后,他們簡化了這個方案,用一個量子點(diǎn)和一個單光子作為輔助來實(shí)現(xiàn)自旋糾纏態(tài)的濃縮[27].2013年,Sheng等[28]進(jìn)一步簡化了自旋糾纏態(tài)濃縮的方案,他們只用一個輔助單光子就可以得到最大糾纏態(tài).同時,基于量子點(diǎn)-腔系統(tǒng)也可以實(shí)現(xiàn)光子態(tài)的糾纏濃縮.在量子點(diǎn)-腔系統(tǒng)中實(shí)現(xiàn)的超糾纏光子態(tài)濃縮在2014年被提出.Ren和Long[29]利用單邊光學(xué)微腔中的量子點(diǎn)自旋實(shí)現(xiàn)了光子偏振和空間模自由度的宇稱檢測,并以此對光子偏振和空間模兩個自由度上的糾纏態(tài)進(jìn)行濃縮.這個方案的成功概率可以通過重復(fù)執(zhí)行糾纏濃縮來進(jìn)一步地提高,而且它可以推廣到n光子超糾纏GHZ態(tài)的糾纏濃縮.

然而,以上的糾纏濃縮方案需要知道部分糾纏態(tài)的系數(shù)或者需要重復(fù)糾纏濃縮過程,這些都降低了糾纏濃縮的效率.本文探討如何利用量子點(diǎn)-腔系統(tǒng)實(shí)現(xiàn)更加高效的光子偏振態(tài)糾纏濃縮.第2部分介紹量子點(diǎn)和雙邊光學(xué)微腔的相互作用;第3部分詳細(xì)介紹光子偏振態(tài)的糾纏濃縮方案;第4部分討論方案的保真度問題;第5部分是本文的總結(jié).

2 量子點(diǎn)和雙邊腔的相互作用

將一個單電子的量子點(diǎn)嵌入光學(xué)微腔中,用抽運(yùn)光對系統(tǒng)進(jìn)行激發(fā)可以產(chǎn)生帶負(fù)電的激子X?,這個激子是由兩個電子的自旋和一個空穴的自旋共同組成的.根據(jù)泡利不相容原理,X?的躍遷由過剩電子的自旋態(tài)控制.這樣會導(dǎo)致兩種圓偏振光經(jīng)過量子點(diǎn)系統(tǒng)時的透射和反射呈現(xiàn)不同的性質(zhì),透射和反射系數(shù)也會有不同的相位和振幅.

雙邊腔是指光學(xué)諧振腔的兩端都可以作為光子的輸出端,量子點(diǎn)被嵌在腔的中心.在雙邊腔系統(tǒng)中,光子的自旋是沿著腔的軸方向(z軸)的.根據(jù)光子自旋的不同,量子點(diǎn)-腔系統(tǒng)會產(chǎn)生兩種典型的躍遷.根據(jù)選擇定則,當(dāng)過剩電子處于自旋向上的|↑〉態(tài),只有|L〉態(tài)的左旋圓偏振光子被吸收,激子處于|↑↓?〉態(tài).如果過剩電子處于自旋向下的|↓〉態(tài),只有右旋圓偏振光子被吸收,激子處于|↓↑?〉態(tài). 其中,|?〉和|?〉分別代表重穴自旋態(tài)|+3/2〉和|?3/2〉.如圖1所示,雙邊光學(xué)腔有兩個輸出端口.

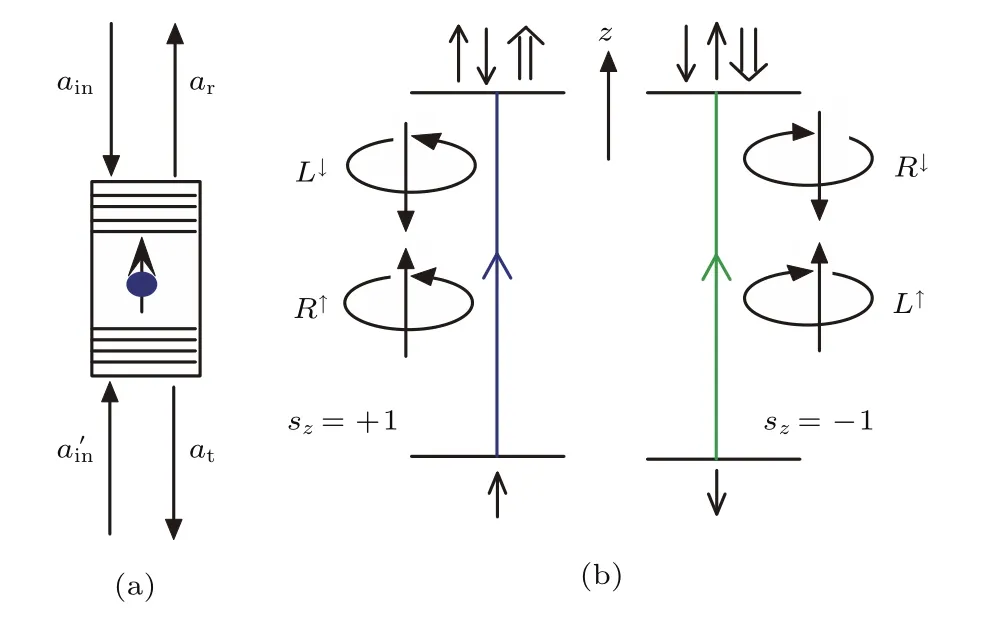
圖1 (a)雙邊腔系統(tǒng)的圓截面,量子點(diǎn)被嵌在腔的中心;(b)量子點(diǎn)-腔系統(tǒng)的能級躍遷和光學(xué)選擇定則(z表示雙邊腔的軸;L和R分別代表光子的左旋和右旋偏振態(tài))Fig.1.(a)The circular cross section of bilateral cavity with a quantum dot embedded in the center;(b)the energy level transition and optical selection rule in quantum dot and cavity system.z is the axis of bilateral cavity.L and R denote the states of the left and right circularly polarized photons,respectively.

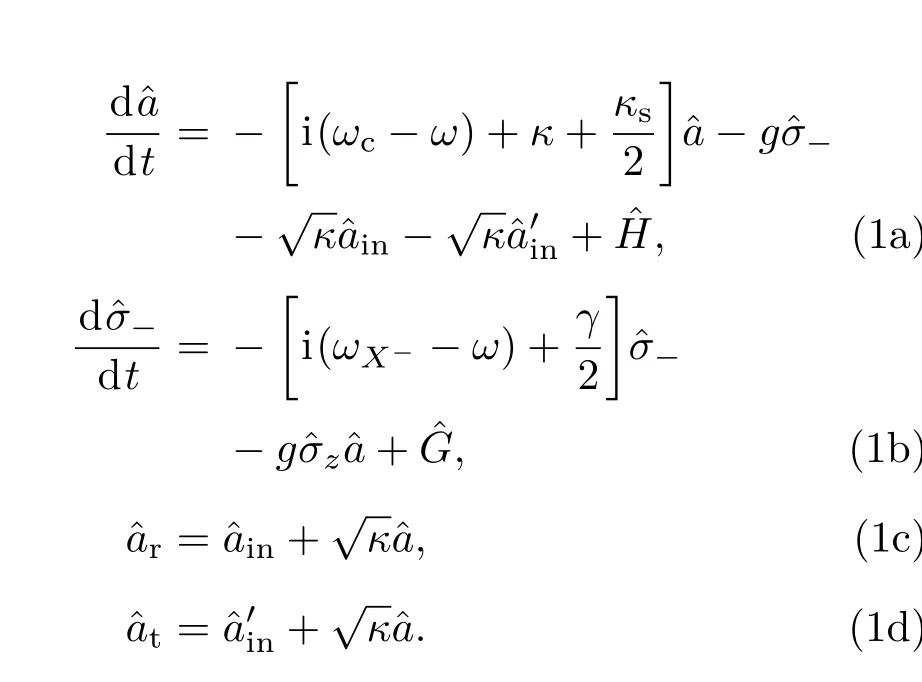
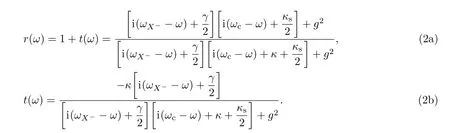
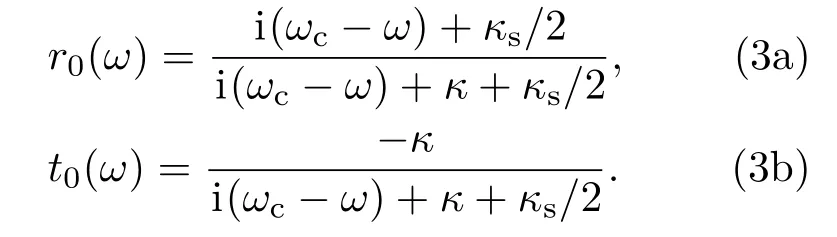
在強(qiáng)耦合和理想共振條件下,可以得到|t(ω)|→0,|t0(ω)|→1,|r(ω)|→1,|r0(ω)|→0.當(dāng)量子點(diǎn)自旋態(tài)處于|↑〉時,sz=+1的光子即處于|R↑〉或|L↓〉的光子,會被反射,光子的偏振方向和傳播方向都發(fā)生變化,變成|L↓〉或者|R↑〉.而sz=?1的光子即處于|R↓〉或|L↑〉的光子會被透射,并伴隨著π相位的翻轉(zhuǎn).類似地,當(dāng)量子點(diǎn)自旋態(tài)處于|↓〉時,sz=?1的光子會被反射,sz=+1的光子會被透射.以上躍遷規(guī)則可以用以下的變換來表示[31,32]:

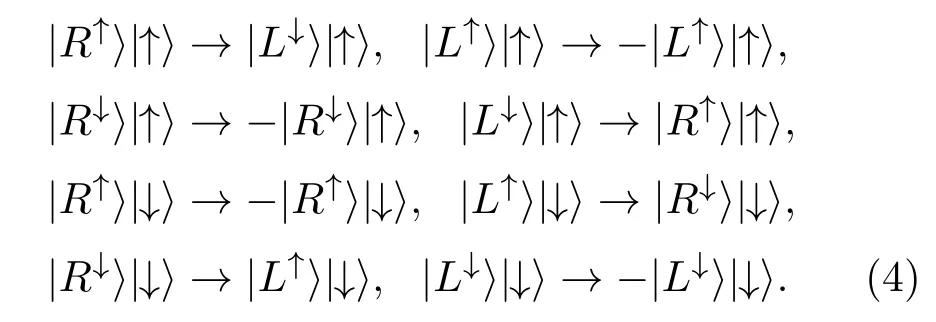
3 光子偏振態(tài)的糾纏濃縮

下面介紹偏振態(tài)糾纏濃縮的原理.假設(shè)兩個距離很遠(yuǎn)的光子處于較低的糾纏態(tài):

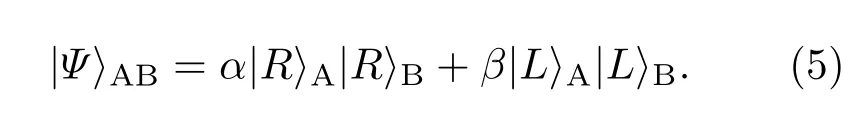
其中|α|2+|β|2=1. 下標(biāo)A(B)分別表示參與者所持有的光子.輔助光子a處于單光子態(tài)|Ψ〉a=|R〉a.兩個量子點(diǎn)中的電子處于自旋態(tài)下標(biāo)s1(2)分別表示在光子A(B)位置的量子點(diǎn).如圖2所示,在光子A處,讓光子a和A依次通過第一個量子點(diǎn).光開關(guān)SW確保光子a首先通過,光子A后通過.光子a和A通過量子點(diǎn)的時間間隔應(yīng)該小于量子點(diǎn)自旋的相干時間.在光子A通過量子點(diǎn)-腔系統(tǒng)之前,需要對自旋態(tài)執(zhí)行一個Hadamard操作,即光子A通過量子點(diǎn)-腔系統(tǒng)后,再對自旋態(tài)執(zhí)行一個Hadamard操作.最終,在通過第一個量子點(diǎn)-腔系統(tǒng)之后,光子和電子自旋的組合態(tài)變?yōu)槿缓?把輔助光子a傳送給參與者B.在光子傳送過程中,由于存在通道噪聲,光子態(tài)會發(fā)生變化:|R〉→γ|R〉+δ|L〉(|γ|2+|δ|2=1). 利用偏振分束器C-PBS將光子通過兩個可能的通道進(jìn)行傳送,并且在傳送前和傳送后都對通道2的光子執(zhí)行σX操作.所以B可能在通道1或者2得到輔助光子a,這時,系統(tǒng)的態(tài)為

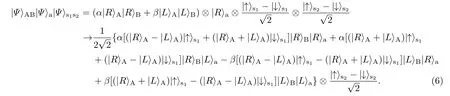
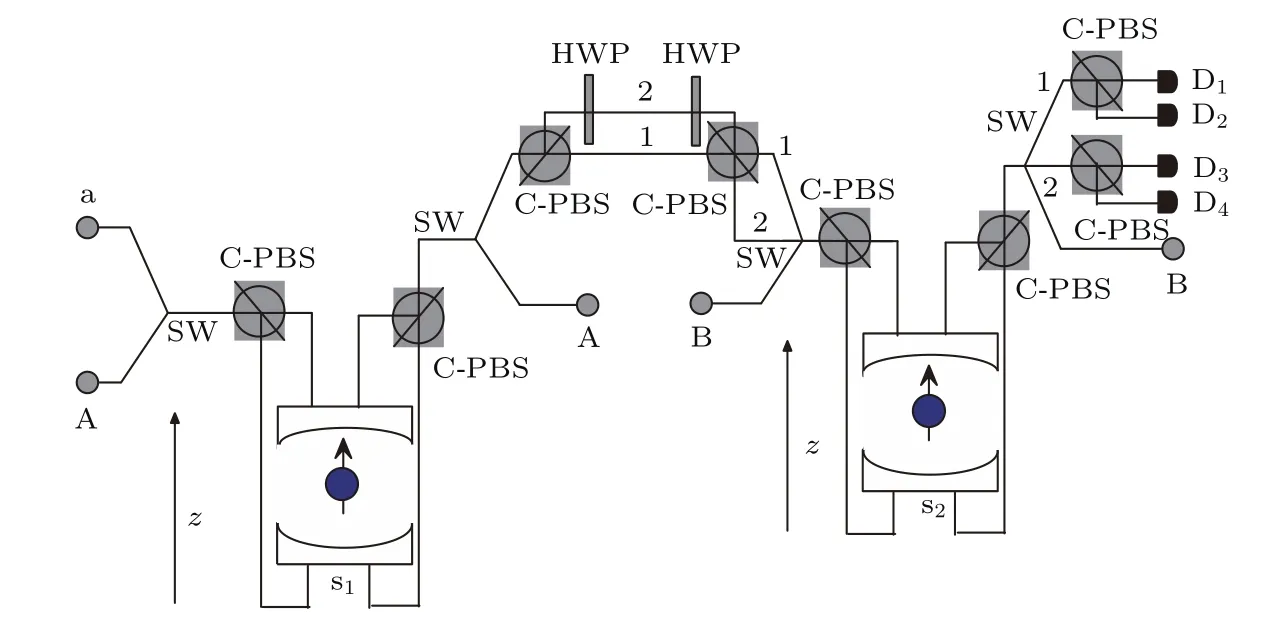
圖2 光子偏振態(tài)糾纏濃縮的示意圖(s1和s2分別代表第一個和第二個量子點(diǎn)的自旋;C-PBS代表偏振分束器,它透射|R〉光子并反射|L〉光子;SW是光開關(guān),它被用來控制光子從不同的路徑輸出;HWP表示對光子執(zhí)行σX操作的半波片;1和2分別代表輔助光子a可能通過的通道;D1,D2,D3和D4是單光子探測器)Fig.2.Schematic of polarization state entanglement concentration.s1and s2are quantum spin states.C-PBS denotes circular polarization beam splitter,transmitting|R〉photon and re fl ecting|L〉photon.SW denotes switch used to control the paths of photon.HWP represents the half wave plate to perform σXon photon.1 and 2 are the possible channels of photon a.D1,D2,D3,and D4are single-photon detectors.

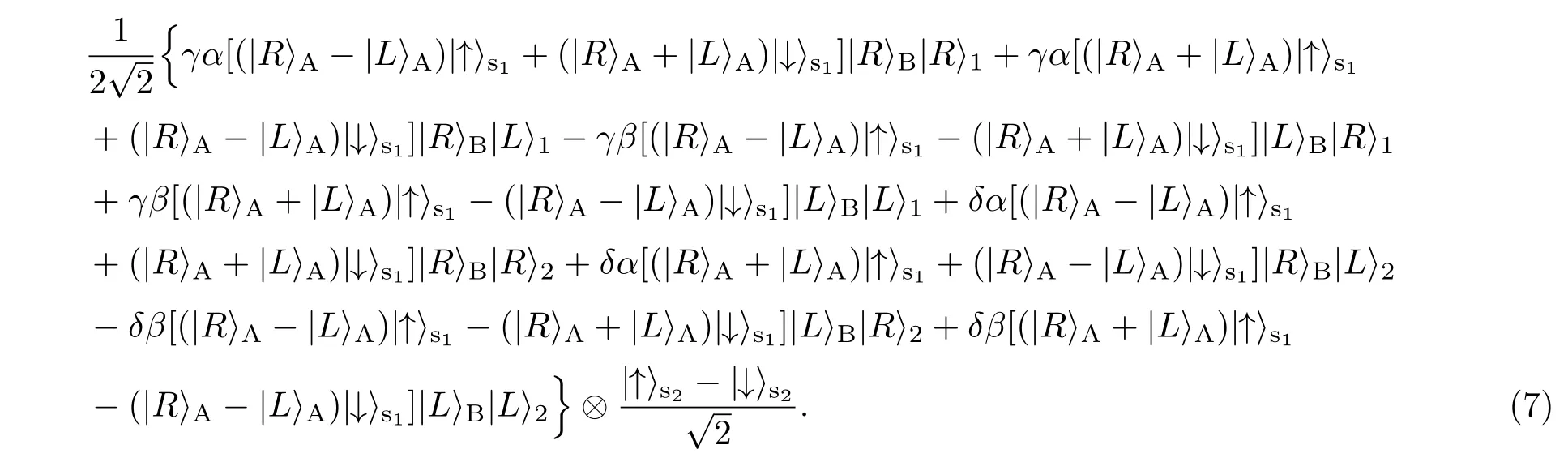
與A類似,參與者B讓光子a和B依次通過第二個量子點(diǎn)-腔系統(tǒng).最后得到:

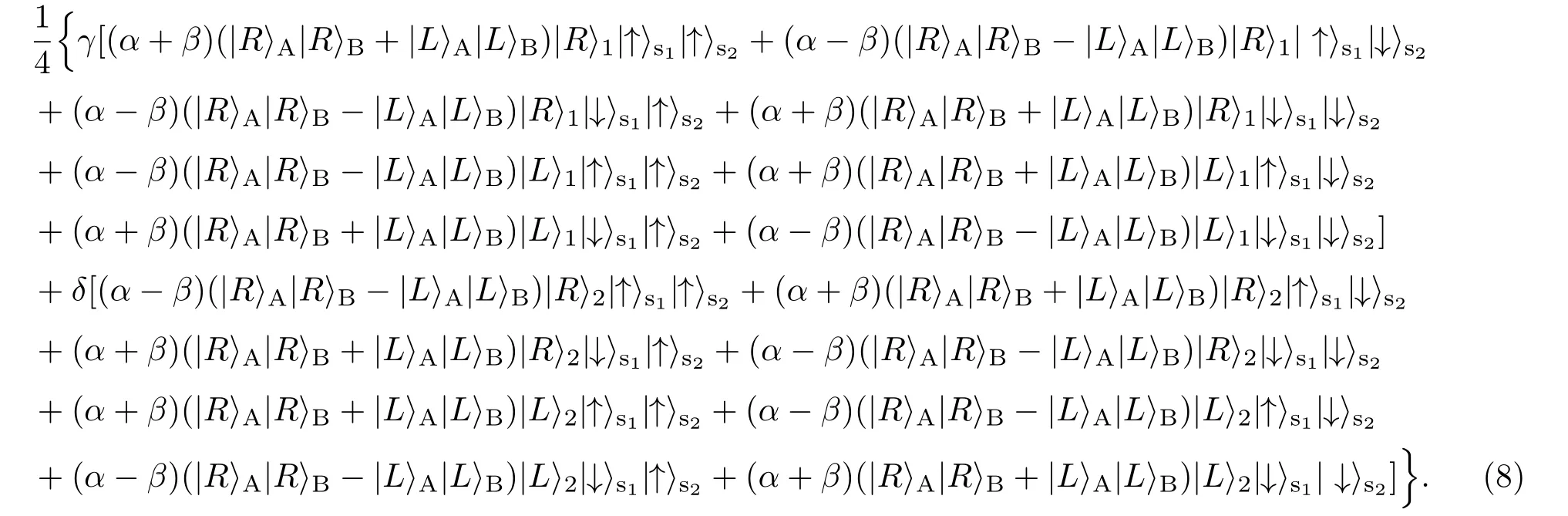
可以看到,根據(jù)兩個量子點(diǎn)自旋態(tài)和輔助光子偏振態(tài)的測量結(jié)果,可以通過相應(yīng)的單光子操作使光子A和B處于最大糾纏態(tài)現(xiàn)在,測量兩個量子點(diǎn)的自旋態(tài)和輔助光子的偏振態(tài),如果得到

4 討 論

以上成功概率是在理想條件下計(jì)算的,沒有考慮量子點(diǎn)-腔系統(tǒng)的耦合強(qiáng)度以及腔的泄漏對方案的影響.如果將耦合強(qiáng)度和腔泄漏率考慮進(jìn)來,則需要計(jì)算系統(tǒng)量子態(tài)的保真度F=|〈Ψf|Ψ〉|2. 這里,|Ψf〉是包含外部環(huán)境影響時系統(tǒng)的最終態(tài),而|Ψ〉是理想條件下的最終態(tài). 本文以|R〉1|↑〉s1|↑〉s2的測量結(jié)果為例,來說明不同的因素對糾纏濃縮的保真度的影響.對于其他15種測量結(jié)果,都可以用同樣的方法計(jì)算得到相對應(yīng)糾纏態(tài)的保真度,得到的結(jié)果是類似的,只是在具體的數(shù)值上有些差異.當(dāng)測量結(jié)果為|R〉1|↑〉s1|↑〉s2時,得到的糾纏態(tài)的保真度為其中,ξ=|t|2(|r|2+|t|2)+|r0|2(|t|?|t0|)2+2|r|2|t||t0|+(|r|2+2|t|2)|t0|2+|t0|4+2|r||r0|(|t0|2?|t|2),ζ=|r0|4+2|r||r0|(|t|2?|t0|2)+|r|2(|r|2+|t|2?2|t||t0|+|t0|2)+|r0|2(2|r|2+|t|2+2|t||t0|+|t0|2).可以看到,F隨著|α?β|變化.|α+β|2+|α?β|2=2,所以圖3是F隨|α?β|的變化曲線.

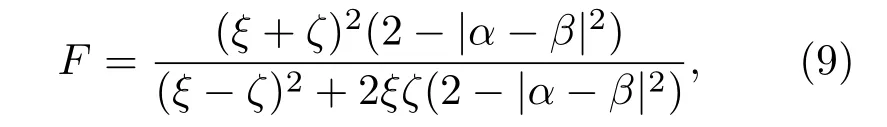
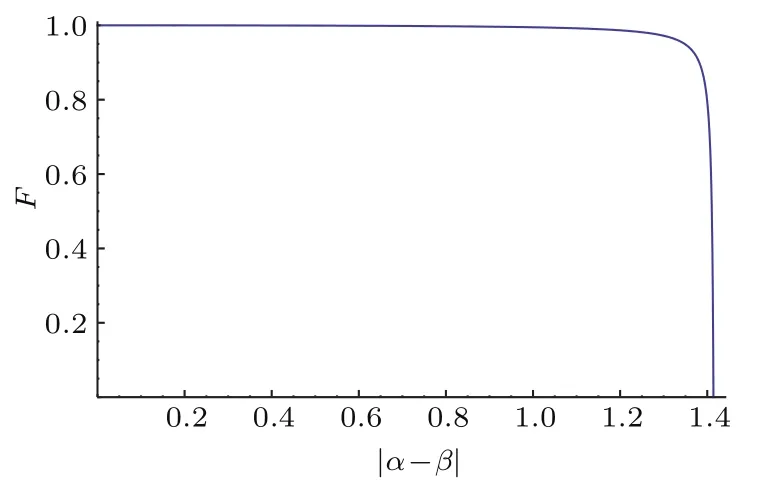
圖3 保真度隨初始糾纏態(tài)系數(shù)的變化曲線(這里選擇腔泄漏率κs/κ=0,量子點(diǎn)-腔系統(tǒng)的耦合強(qiáng)度g/κ=1,并且γ/κ =0.2)Fig.3.The curve of fi delity vs initial coefficients of entangled state.The cavity leakage is chosen to be κs/κ =0,and coupling strength g/κ =1 with γ/κ =0.2.

從圖3可以看出:當(dāng)|α?β|≤ 1.3時,F變化很小,并保持接近于1的值.當(dāng)|α?β|=1.3時,F=0.972;然而,當(dāng)|α?β|＞1.3時,F將隨著|α?β|的增加急劇減小.所以在|α?β|≤ 1.3時,本文的糾纏濃縮方案受部分糾纏態(tài)的初始信息影響很小,可以實(shí)現(xiàn)任意未知糾纏態(tài)的濃縮;然而,時,本文的方案保真度較小.

同時,保真度F也會受到耦合強(qiáng)度g/κ和腔邊泄漏率κs/κ的影響,如圖4所示.

圖4 (網(wǎng)刊彩色)保真度隨耦合強(qiáng)度和腔泄漏的變化(這里,選擇|α?β|=1)Fig.4.(color online)The curve of fi delity vs coupling strength and cavity leakage.Here,|α?β|=1.

從圖4可以看出,F的最小值為0.5.在弱耦合條件(g/κ＜0.5)下,F的值較小,而且受腔泄漏的影響非常大.而在腔強(qiáng)耦合條件(g/κ＞0.5)下,F接近于1,而且可以保持穩(wěn)定,幾乎不受腔泄漏的影響.弱耦合g/κ=0.3的情況下,當(dāng)κs/κ=0時,成功概率F=66.34%.強(qiáng)耦合g/κ=1.5條件下,當(dāng)κs/κ=0時,F=99.81%.當(dāng)g/κ=2.4時,相對于κs/κ=0或0.1,F=99.97%或者99.86%.當(dāng)g/κ＞0.7時,F趨于穩(wěn)定,不會隨著耦合強(qiáng)度和泄漏率的增加有太大的變化.所以本文的糾纏濃縮方案對腔的邊泄漏率要求不高,而且只要滿足g/κ＞0.7,繼續(xù)增加耦合強(qiáng)度也沒有實(shí)際意義.系統(tǒng)的耦合強(qiáng)度取決于帶電激子的振蕩強(qiáng)度和微腔的模體積,量子點(diǎn)和光學(xué)微腔的弱耦合在實(shí)驗(yàn)室比較容易實(shí)現(xiàn),強(qiáng)耦合實(shí)現(xiàn)起來雖有一些難度,但近年來也取得了很大進(jìn)展.在直徑d=1.5μm的微柱形光學(xué)微腔中,g?0.5(κ+κs)的耦合強(qiáng)度已經(jīng)實(shí)現(xiàn)[33],對應(yīng)的腔品質(zhì)因子Q=8800.當(dāng)腔的直徑d=2μm時,其品質(zhì)因子可以達(dá)到Q=4×104[34],通過改善樣品的設(shè)計(jì)和制備方法,耦合強(qiáng)度可以達(dá)到g?2.4(κ+κs)[35].現(xiàn)有的條件已經(jīng)可以滿足實(shí)驗(yàn)的要求,本文的方案是可行的.

5 結(jié) 論

本文利用兩個微腔中的量子點(diǎn)和一個光子作為輔助,實(shí)現(xiàn)了光子偏振非最大糾纏態(tài)的濃縮,得到了最大糾纏態(tài).首先,利用光開關(guān)讓輔助光子a和光子A依次與第一個量子點(diǎn)相互作用,再將光子a通過兩個可能的通道傳送給第二個參與者,以確保光子a的量子態(tài)不受通道噪聲的影響;然后讓光子a和B依次與第二個量子點(diǎn)相互作用;最后對兩個量子點(diǎn)的自旋態(tài)和輔助光子的偏振態(tài)進(jìn)行測量,根據(jù)測量結(jié)果對光子對AB執(zhí)行相應(yīng)的操作即可得到最大的偏振糾纏態(tài).在不考慮腔邊泄漏的理想情況下,方案的成功概率為1. 本文也以|R〉1|↑〉s1|↑〉s2的測量結(jié)果為例計(jì)算了方案的保真度,結(jié)果顯示本文的糾纏濃縮方案在耦合強(qiáng)度g/κ＞0.7時可以達(dá)到99.8%以上,而且受腔泄漏的影響也很小.在實(shí)際的量子通信過程中,要得到初始糾纏態(tài)的系數(shù)信息,需要兩個參與者可對足夠數(shù)量光子對進(jìn)行測量,這樣消耗大量的糾纏資源.本文的糾纏濃縮方案中,初始糾纏態(tài)的系數(shù)影響很小,可以忽略,這就避免了糾纏資源的浪費(fèi).而且本方案不需要重復(fù)執(zhí)行,大大簡化了糾纏濃縮的過程.這些特點(diǎn)都增加了糾纏濃縮的通用性和效率,進(jìn)而保證了量子糾纏態(tài)的品質(zhì).量子糾纏濃縮可以在一定程度上消除消相干作用造成的糾纏態(tài)品質(zhì)下降,使得兩個參與者共享的是最大糾纏態(tài),這在遠(yuǎn)距離量子通信中是非常有用的,可以提高量子隱形傳送、量子密鑰分配、量子密碼學(xué)等方案的安全性.量子糾纏濃縮在可容錯量子計(jì)算和分布式量子計(jì)算中也有著極其重要的應(yīng)用.

[1]Bennett C H,Bernstein H J,Popescu S,Schumacher B 1996Phys.Rev.A53 2046

[2]Guo R,Zhou L,Gu S P,Wang X F,Sheng Y B 2016Chin.Phys.B25 030302

[3]Zhang W Z,Li W D,Shi P,Gu Y J 2011Acta Phys.Sin.60 060303(in Chinese)[張聞釗,李文東,史鵬,顧永建2011物理學(xué)報60 060303]

[4]Zhou L,Wang D D,Wang X F,Gu S F,Sheng Y B 2017Chin.Phys.B26 020302

[5]Zhao Z,Pan J W,Zhan M S 2001Phys.Rev.A64 014301

[6]Yamamoto T,Koashi M,Imoto N 2001Phys.Rev.A64 012304

[7]Bose S,Vedral V,Knight P L 1999Phys.Rev.A60 194

[8]Sheng Y B,Deng F G,Zhou H Y 2008Phys.Rev.A77 062325

[9]Sheng Y B,Zhou L,Zhao S M,Zheng B Y 2012Phys.Rev.A85 012307

[10]Ding S P,Zhou L,Gu S P,Wang X F,Sheng Y B 2017Int.J.Theor.Phys.56 1912

[11]Qu C C,Zhou L,Sheng Y B 2015Quant.Inf.Process.14 4131

[12]Fei S M 2016Sci.China:Inform.Sci.59 128501

[13]Song T T,Tan X,Wang T 2017Sci.Rep.7 1982

[14]Ren B C,Du F F,Deng F G 2013Phys.Rev.A88 012302

[15]Cao C,Wang T J,Mi S C,Zhang R,Wang C 2016Ann.Phys.369 128

[16]Du F F,Deng F G,Long G L 2016Sci.Rep.6 35922

[17]Loss D,DiVincenzo D P 1998Phys.Rev.A57 120

[18]Wei H R,Deng F G 2013Opt.Express21 17671

[19]Chen Q C 2016Acta Phys.Sin.65 247801(in Chinese)[陳秋成 2016物理學(xué)報65 247801]

[20]Wang S X,Li Y X,Wang N,Liu J J 2016Acta Phys.Sin.65 137302(in Chinese)[王素新,李玉現(xiàn),王寧,劉建軍2016物理學(xué)報65 137302]

[21]Wei H R,Deng F G 2013Phys.Rev.A87 022305

[22]Senellart P,Solomon G,White A 2017Nat.Nanotechnol.12 1026

[23]Ren B C,Deng F G 2014Sci.Rep.4 4623

[24]Shimizu H,Saravanan S,Yoshida J,Ibe S,Yokouchi N 2006Appl.Phys.Lett.88 241117

[25]Ulbrich N,Bauer J,Scarpa G,Boy R,Schuh G,Abstreiter G,Schmult S,Wegscheider W 2003Appl.Phys.Lett.83 1530

[26]Wang C,Zhang Y,Jin G S 2011Phys.Rev.A84 032307

[27]Wang C 2012Phys.Rev.A86 012323

[28]Sheng Y B,Zhou L,Wang L,Zhao S M 2013Quant.Inf.Process.12 1885

[29]Ren B C,Long G L 2014Opt.Express22 6547

[30]Scully M O,Zubairy M S 1997Quantum Optics(Cambridge:Cambridge University Press)

[31]Hu C Y,Munro W J,O’Brien J L,Rarity J G 2009Phys.Rev.B80 205326

[32]Bonato C,Haupt F,Oemrawsingh S S R,Gudat J,Ding D,van Exter M P,Bouwmeester D 2010Phys.Rev.Lett.104 160503

[33]Reithmaier J P,Se?k G,L?ラer A,Hofmann C,Kuhn S,Reitzenstein S,Keldysh L V,Kulakocskii V D,Reinecke T K,Forchel A 2004Nature432 197

[34]Yoshie T,Scherer A,Hendrickson J,Khitrova G,Gibbs H M,Rupper G,Ell C,Shchekin O B,Deppe D G 2004Nature432 200

[35]Reitzenstein S,Hofmann C,Gorbunov A,Strau? M,Kwon S H,Schneider C,L?ラer A,H? fl ing S,Kamp M,Forchel A 2007Appl.Phys.Lett.90 251109