Impact of SST Anomaly Events over the Kuroshio–Oyashio Extension on the “Summer Prediction Barrier”
Yujie WUand Wansuo DUANLaboratory for Climate Studies,National Climate Center,China Meteorological Administration,Beijing 0008,China
2State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics(LASG),Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China
3CMA-NJU Joint Laboratory for Climate Prediction Studies,Nanjing University,Nanjing 210023,China
4University of Chinese Academy of Sciences,Beijing 100049,China
1.Introduction
Better understanding of the climate predictability over areas with significant ocean–atmosphere interaction is of great importance in improving the performance and forecast skill of numerical models.Considerable effort has been invested in exploring the predictability of El Ni?o–Southern Oscillation(ENSO)events and Indian Ocean Dipole(IOD)events(Webster and Yang,1992;Lau and Yang,1996;McPhaden,2003;Luo et al.,2007;Feng et al.,2014;Yang et al.,2015),both of which have global climatic and social impacts(Cane,1983;Philander,1983;Dai and Wigley,2000;Curtis and Adler,2003;Yamagata et al.,2004;Chang et al.,2006;Schott et al.,2009).The “spring predictability barrier”,which refers to the phenomenon that most ENSO prediction models often experience an apparent drop in prediction skill across boreal spring(Webster and Yang,1992;Latif et al.,1994),is a well known characteristic of ENSO forecasts.In numerical forecasts of IOD events,the prediction skill often drops rapidly across boreal winter regardless of the starting month,indicating the existence of a “winter predictability barrier”(Feng et al.,2014).The existence of a “spring predictability barrier”and “winter predictability barrier”often lead to unsuccessful forecasts of ENSO and IOD events,respectively(Webster and Yang,1992;Latif et al.,1994;Luo et al.,2007),which in turn greatly restricts the prediction skill of climate variability in the tropical Pacific and Indian oceans.
The SST anomalies(SSTA)over the Kuroshio–Oyashio Extension(KOE)play a critical role in the ocean–atmosphere interaction in the North Pacific(Gan and Wu,2012).However,the forecast skill of SSTA in the KOE region is quite poor(Guemas et al.,2012;Wen et al.,2012),which seriously limits the predictability of North Pacific SSTA.The low predictability of SSTA in the KOE region is possibly due to its weakest“memory”being in the boreal summer(Motokawa et al.,2010;Zhao et al.,2012)and the fastest error growth when bestriding the boreal summer in numerical forecasts[i.e.,the “summer prediction barrier”described in Duan and Wu(2015)].The “summer prediction barrier”(SPB)refers to the phenomenon that the prediction errors of SSTA in the central and western North Pacific always increase rapidly in the August–September–October(ASO)season,and ultimately cause large prediction uncertainties at prediction times.Similar to the impact of the“spring predictability barrier”on ENSO forecasts and the “winter predictability barrier”on IOD forecasts,the SPB is considered to be one of the main factors limiting the predictability of North Pacific SSTA(Duan and Wu,2015;Wu et al.,2016).Therefore,more comprehensive knowledge about the SPB is needed to understand the SSTA predictability in the North Pacific,as well as in the KOE region.
In Duan and Wu(2015),the physical and dynamical mechanisms were explored by primarily focusing on the influence of the climatological mean state and initial errors on the rapid error growth associated with the SPB.However,they did not discuss in depth the impact of the reference states[i.e.,the KOE-SSTA events described in Wu et al.(2016)]on the occurrence of the SPB.KOE-SSTA events are defined as SSTA in the KOE region(30°–50°N,145°E–150°W)larger(smaller)than 0.25 K(?0.25 K)persisting for at least five months(Wu et al.,2016).The SSTA of these events are usually established in boreal spring and reach their peak in boreal summer(Duan and Wu,2015).The transition from the mature to decaying phase always occurs in the ASO season,which is the period when the error growth associated with the SPB is most significant.That is,the prediction errors associated with the SPB usually increase rapidly during the mature-to-decaying transition phase of the SSTA events to be predicted.It is therefore hypothesized that the evolutionary characteristics in the transition phase of KOESSTA events probably have impacts on the SPB.Accordingly,in this paper,we attempt to address the influence of KOE-SSTA events(especially the evolutionary characteristics in the mature-to-decaying transition phase)on the SPB,and further explore the related physical and dynamical mechanisms,which may be helpful in better understanding the SPB and the predictability of North Pacific SSTA.Herein,we investigate these issues by analyzing the results of perfect model predictability experiments in a fully coupled global model.In section 2,we briefly describe the model and approach used in our study.The impact of KOE-SSTA events on the occurrence of the SPB is reported in section 3.In section 4,we investigate the mechanisms responsible for the influence of KOE-SSTA events on the SPB.And finally,a summary of the key findings is presented in section 5.
2.Model and strategy
In this study,the Fast Ocean Atmosphere Model[FOAM;Jacob(1997)]is used to perform perfect model predictability experiments.FOAM is a fully coupled global model:the atmospheric component has a horizontal resolution of 7.2°longitude× 4.75°latitude and 18 levels in the vertical direction;the ocean component has a horizontal resolution of 1.4°latitude× 2.8°longitude and 32 vertical levels.A detailed description of FOAM is available in Wu et al.(2016).FOAM simulates the large-scale sea temperatures and atmospheric circulation of the KOE region well,and the simulation of KOE-SSTA events is also quite reasonable(Duan and Wu,2015).Thirty12-month-long KOE-SST Aevents,including 15 warm ones and 15 cold ones,are randomly selected from the long-term control run of the fully coupled simulation of FOAM,and regarded as the reference states(i.e.,the “true states”)to be predicted.Figures 1a and b respectively show the selected warm and cold SSTA events,illustrating that the SSTA of these events are established in boreal spring,reach their peak in boreal summer,and start to transfer to the decaying phase from the ASO season.In addition,some of the KOE-SSTA events rapidly transfer from the mature to decaying phase,with a transition rate(blue bars in Figs.1a and b)larger than 0.3 K month?1during the ASO season,while other events less so(red bars in Figs.1a and b).The composite spatial patterns of SSTA and related wind stress anomalies for the warm events of the two categories shown in Fig.1a are illustrated in Figs.1c and d.It is apparent that warm SSTA in the KOE region decay very rapidly and almost disappear when leading by six months for Category-1 events(Fig.1c).However,the warm SSTA of Category-2 events persist for more than six months after the peak phase(Fig.1d).Therefore,the KOE-SSTA events to be predicted can be classified into two categories based on their mature-to-decaying transition rates:Category-1(blue lines in Figs.1a and b)includes SSTA events with transition rates larger than 0.3 K month?1in the ASO season;and Category-2(red lines in Figs.1a and b)comprises SSTA events with relatively smaller transition rates.Statistically,there is a total of 56 typical KOE-SSTA warm events and 49 cold events in a 200-year control run of FOAM,and the percentage of warm(cold)events in Category-1 is about 58.9%(51.0%).Similar features of KOE-SSTA events can be found in observations(ERSST.v3b/NOAA during 1950–2014):the percentage of warm(cold)events in Category-1 is about 60.0%(57.1%)events(data not shown),which is similar to the FOAM-simulated results.To investigate which kinds of KOE-SSTA events are more likely to yield a significant SPB,two groups of perfect model predictability experiments are conducted by predicting the SSTA events in Category-1 and Category-2 for 12 months with perturbed initial fields starting from Nov(?1)[i.e.,November in Year(?1)],Feb(0)[i.e.,February in Year(0)],May(0),and Aug(0).Year(0)denotes the year when the SSTA events attain their peak value,and Year(?1)is the year before Year(0).The difference between these two experiments(referred to asand)lies in the approaches of constructing initial perturbations(i.e.,initial errors).
In Exp Reference,the approach of constructing initial errors is to calculate the differences between the North Pacific sea temperature fields(20°–60°N,120°E–100°W)in the start months of the predictions and other months.As described in Duan and Wu(2015),the warm–cold cycle of the SSTA in the KOE region has a dominant period of three years.It is conceivable that the initial errors also follow a three-year(36-month)oscillation period when the start month of a prediction is given.Therefore,in order to adopt as many initial errors as possible,for every SSTA event we construct 36 initial errors by calculating the differences between the North Pacific sea temperature fields at five levels(surface,40 m,60 m,80 m,and 100 m)in its start month and the successive 36 months before the start month.The initial errors are scaled to the same magnitude,which is about 30%–50%of the initial anomalies,following Duan and Wu(2015).For convenience,we call the initial errors obtained by this method the Ref-type initial errors.is similar to Exp Reference,except it uses 36 random initial errors.For every random initial error in,the initial error at each grid point is randomly selected from a time series obeying the normal distribution with an average of zero and a standard deviation the same as the Ref-type initial errors.In Exp Random,all the SSTA events in Category-1 and Category-2 are predicted with the 36 random initial errors.is conducted to con fi rm the robustness of the results in.Ultimately,a total of 144 predictions with four start months and 36 Ref-type initial errors(36 random initial errors)can be obtained for every SSTA event in.By analyzing the results of these predictions,we investigate the impact of the SSTA events in Category-1 and Category-2 on the SPB.
3.Impact of the SSTA events to be predicted on the SPB
As in Duan and Wu(2015),the monthly error growth rates of the SSTA events at time t(t=1,2,···12 months)are roughly estimated by

in which the magnitude of the prediction error is calculated by
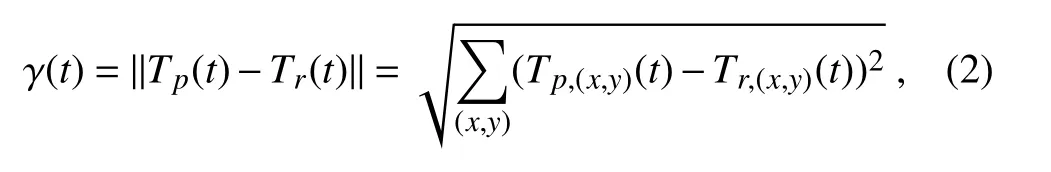
(x,y)represent the longitude and latitude in the KOE region,and Tr(t)and Tp(t)are the SSTA of warm or cold events and their predictions,respectively.The large absolute value of κ(t)corresponds to the fast error increase or decrease.The seasonal growth rates of prediction errors can be obtained by calculating the sum of the error growth rates during different seasons.To investigate the results of the experiments,the criteria of an SPB in this paper are as follows:(1)the error growth rate in the ASO season(i.e.,κASO)is larger than the error growth rate in any other season;(2)the prediction error measured by γ(t)in the ASO season is five times larger than the magnitude of the initial error( five times the initial error is roughly equivalent to two times the standard deviation of KOE-SSTA).The predictions simultaneously satisfying these two criteria can be regarded as reflecting the occurrence of an SPB.
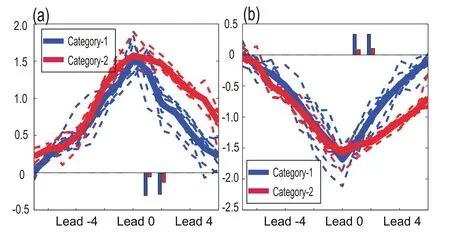
Fig.1.(a)The warm KOE-SSTA events in Category-1(dashed blue lines;units:K)and Category-2(dashed red lines;units:K)and their ensemble means(solid blue line for-Category-1 and solid red line for Category-2).The blue(red)bars represent the mature-to-decaying transition rates(units:K month?1)for Category-1(Category-2).(b)As in(a)but for cold events.The warm(cold)KOE-SSTA events in(a,b)are randomly selected from the long-term control run of the fully coupled simulation of FOAM according to the definition in section 1.(c)The composite spatial patterns of SSTA(contours;units:K)and sea surface wind stress anomalies(vectors;units:0.1 N m?2)for the KOE-SSTA warm events in Category-1 shown in(a).(d)As in(c)but for the warm events in Category-2 shown in(a).Color shading in(c,d)represents the 95%confidence level.The lead“0”represents the month when the events attain their peak and the leads“?6(6)”,“?4(4)”and “?2(2)”denote the 6th,4th and 2nd month before(after)the peak month.The black rectangle marks the KOE-SSTA region(30°–50°N,145°E–150°W)which is the study area in this paper.

Fig.1.(Continued)
3.1.Results from Exp Reference
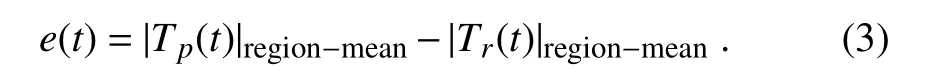
It is illustrated that although the error growth rates in the ASO season for all the KOE-SSTA events in the two categories are larger than in the other seasons,the magnitudes of κASOfor the SSTA events in Category-1 are significantly larger than those in Category-2.As reported in Duan and Wu(2015),the rapid error growth in the ASO season is the most typical feature of the SPB,and the large prediction uncertainties associated with the SPB are largely contributed by the error growth in the ASO season.That is,the rapid error growth in the ASO season usually implies a significant SPB.So,the magnitude of the error growth rate in the ASO season κASOcan be used to measure the intensity of the SPB,wherein a larger κASOrepresents a more significant SPB.Therefore,the results shown in Fig.2 indicate that SSTA events transferring more rapidly from the mature to decaying phase(i.e.,the SSTA events in Category-1)tend to yield a more significant SPB than those events with smaller transition rates(i.e.,the SSTA events in Category-2).
Furthermore,as mentioned in section 2,every KOESSTA event has 36 predictions initiated with Ref-type perturbations for each start month.Thus,for every SSTA event,the amount among the 36 predictions that have an SPB can be approximately considered as a measurement of the likelihood that an SPB occurs,i.e.,the more predictions exhibiting an SPB,the more likely one is to occur.Figure 3 illustrates the amount of predictions with an SPB for every SSTA event in the two categories,initiated from different start months,in.It is clear that the SSTA events in Category-1 possess many more predictions exhibiting an SPB than those in Category-2,indicating that SSTA events with larger mature-to-decaying transition rates are more likely to yield an SPB than those with smaller rates.

Fig.2.(a)The seasonal error growth rates measured by κ(t)described in section 3 of every KOE-SSTA event in Category-1 and Category-2.(b)As in(a)but for the growth rates of regional-mean KOE-SSTA errors(units:K month?1).The results of every SSTA event are the ensemble mean of the predictions initiated from Feb(0)with 36 Ref-type initial errors in Exp Reference.It should be noted that the error growth rates for cold events shown in(b)are calculated by(?1)×to visually compare with the result of warm events.
Therefore,the results of Fig.2 and Fig.3 allow us to conclude that if the KOE-SSTA events transfer more rapidly from the mature to decaying phase, they tend to have a greater possibility of a more significant SPB.This implies that forecasting KOE-SSTA events in Category-1 may be much less successful,due to the significant SPB,especially when the forecasts are made before and through their transition phase,which is usually during the ASO season.In addition,we also predict the SSTA events in Category-1 by perturbing their initial fields with the Ref-type initial errors of the SSTA events in Category-2,or vice versa.The results show that the SSTA events in Category-1 tend to have a greater possibility of a more significant SPB,despite their initial fields being perturbed by the Ref-type initial errors that often fail to cause an SPB for the SSTA events in Category-2.However,the SSTA events in Category-2 have less possibility of yielding an SPB when predicted with the initial errors causing the SPB of the SSTA events in Category-1.These results further demonstrate the robustness of the conclusion reported in this paper.
3.2.Results from Exp Random
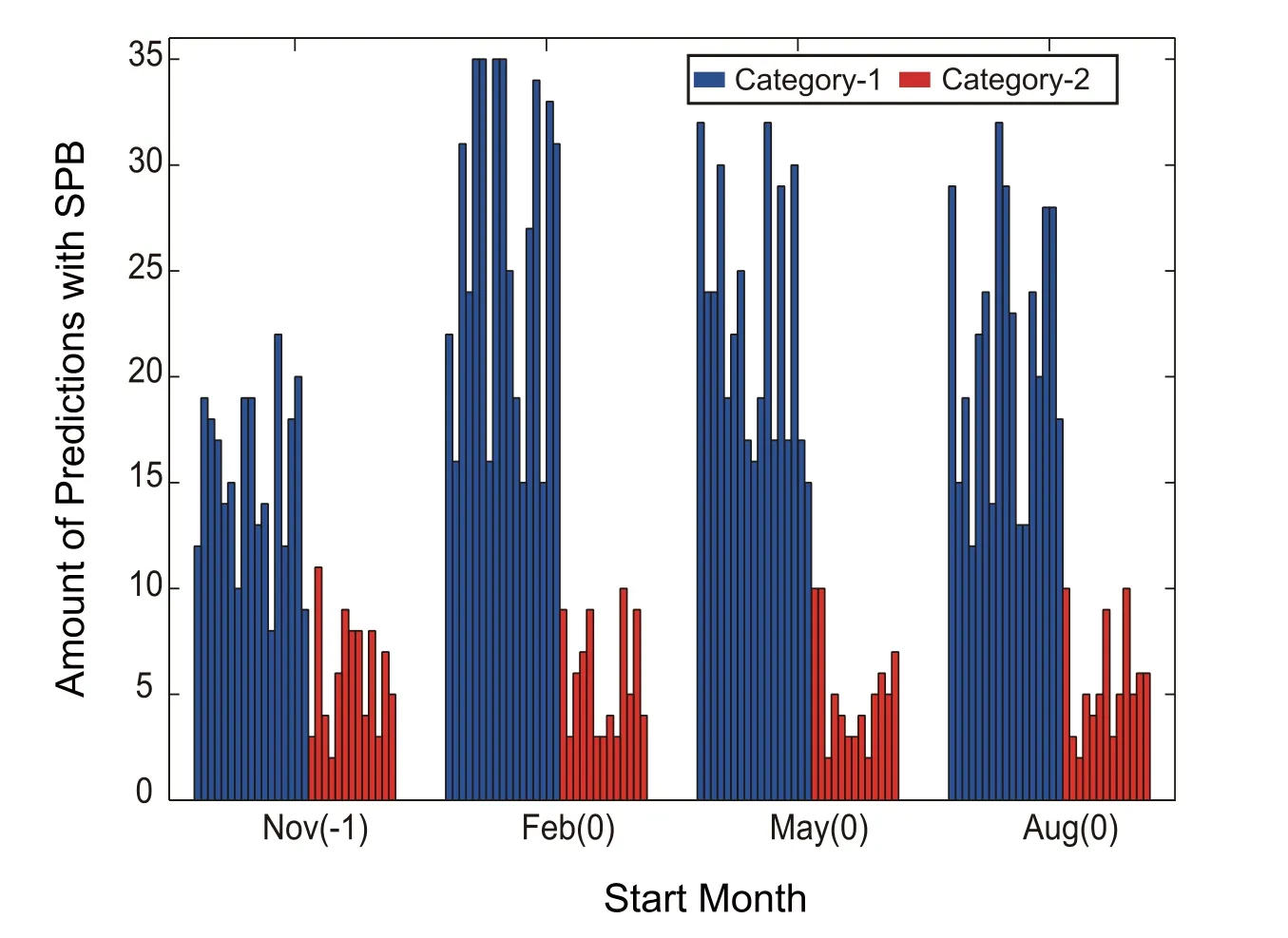
Fig.3.Each of the bars represents the amount of predictions with an SPB among the 36 predictions for every KOE-SSTA event shown in Figs.1a and b.The 36 predictions for every SSTA event are obtained by predicting with 36 Ref-type initial errors in Exp Reference from each of the initial months shown on the horizontal axis.The blue(red)bars represent the results of 17(13)KOE-SSTA warm and cold events in Category-1(Category-2)in Figs.1a and b.
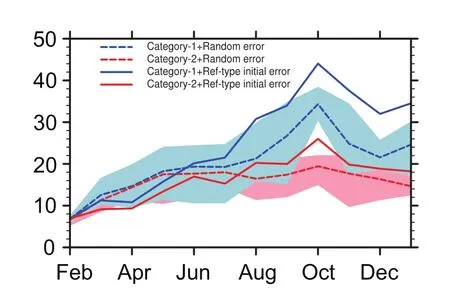
Fig.4.The ensemble mean of monthly prediction errors by predicting the SSTA events in Category-1(blue lines)and Category-2(red lines)with random initial errors(dashed lines)and Ref-type initial errors(solid lines)initiated from Feb(0).The ensemble error evolutions(shaded area)for the predictions with random initial errors are also shown.The measurement of prediction errors is the same as that in section 3.
4.Possible mechanisms
Why do the KOE-SSTA events with larger mature-to decaying transition rates have a greater possibility of yielding a more significant SPB?What is the relationship between the transition rate of SSTA events and the error growth rate associated with the SPB?To address these issues,we explore which physical processes are responsible for the error growth associated with the SPB and compare their differences between the KOE-SSTA events in the two categories.
Duan and Wu(2015)explored the physical mechanisms responsible for the SPB through mixed-layer heat budget analysis based on the equation governing the mixed-layer temperature,which is a good proxy for SST.The equation can be expressed as:
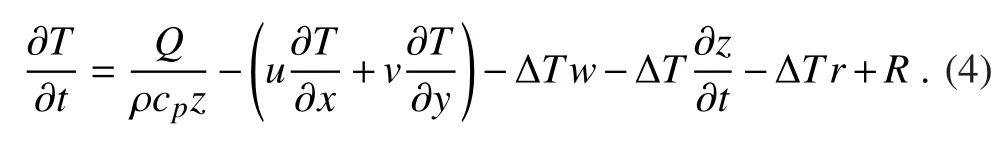
On the right-hand side of Eq.(4),Q in the first term represents the net sea surface heat flux;ρ,cpand z are respectively the density of sea water,the Specific heat capacity and the mixed-layer depth,which is defined as the layer depth where the sea temperature is 0.5°C less than the SST.The second term,?[u(?T/?x)+v(?T/?y)],is the horizontal advection by zonal velocity u and meridional velocity v.In the third term,?ΔTw,ΔT=(T ?T(?z))/z is the entrainment due to the vertical velocity w. The vertical advection induced by the Ekman pumping is one component of this entrainment term because the Ekman pumping is the vertical velocity induced by the wind-stress curl and w implicitly includes the vertical velocity due to the wind stress.On seasonal to annual timescales,the vertical velocity field is usually considered as naturally filtered,and is then approximately equal to the vertical Ekman advection,i.e.,(de Boisséson et al.,2010).The analysis of this study mainly focuses on seasonal timescales.Therefore,this entrainment term in this study is dominated by the vertical advection induced by Ekman pumping.The fourth and fifth terms are respectively the entrainment due to the tendency of the mixed layer depth and the entrainment due to “advection of the mixed layer depth”,in which r= ?[u(?z)/(?x)+v(?z)/(?y)].The last term includes the turbulent mixing and heat diffusion.In the heat budget analysis of KOE-SSTA events(not shown here),it is found that the SSTA tendency of KOE-SSTA events is largely dominated by the net sea surface heat flux,the vertical advection and the horizontal advection.The contributions of the entrainment terms(i.e.,?ΔT(?z/?t)and ?ΔTr)and the turbulent mixing and heat diffusion term R are negligible,which thus can be neglected in our following analysis.Therefore,the equation governing the evolution of KOE-SSTA prediction errors can be expressed as:

in which,
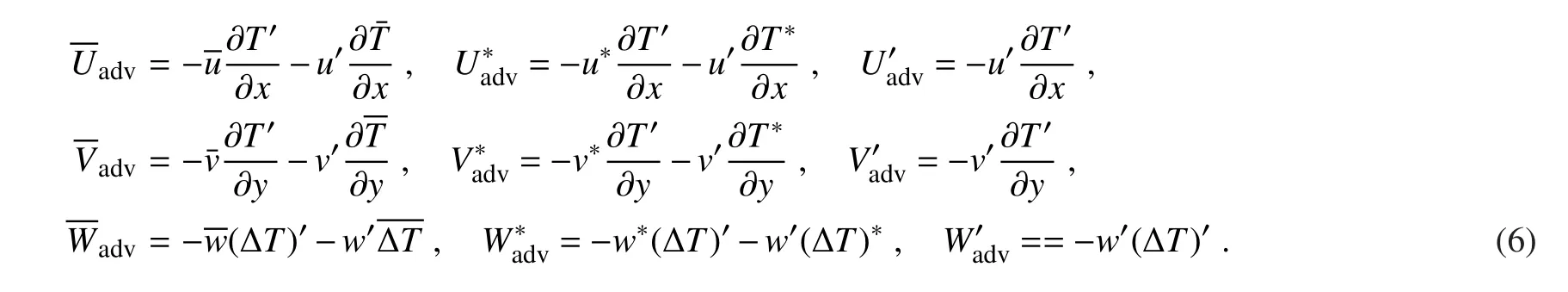
In Eqs.(5)–(6),the climatological mean state,the anomaly and the error are respectively denoted by an over bar,asterisk and prime.Q′represents the sea surface heat flux error and is the sum of the latent heat flux errorsensible heat flux error,shortwave radiation flux error,and long wave radiation flux erroris the climatological monthly mean mixed-layer depth.As in observations(Wang et al.,2012),the simulatedin the KOE region is deeper than 150 m in boreal winter and shallower than 30 min boreal summer.The terms in Eq.(6)indicate the effects of oceanic temperature advection on the SSTA error growth.Duan and Wu(2015)revealed that the latent heat flux errorsand the vertical oceanic temperature advection associated with the climatological mean statewhich are both largely forced by the sea surface wind stress errors,dominate the SSTA error growth associated with the SPB.Clearly,the effects of bothandon the error growth are directly influenced by the climatological annual cycle and prediction errors,but not the SSTA events to be predicted.In Figs.5a and b,we show the ensemble means ofandaveraged over the KOE region in the ASO season for the warm and cold events in Category-1(black bars)and Category-2(gray bars),respectively.They both have few differences between the two categories(differences shown in Fig.5e),indicating that the larger error growth rates of the SSTA events in Category-1 are not due to the physical processes ofand.Furthermore,the termsandadvare not directly influenced by the SSTA events to be predicted and make little contribution to the different error growth rates between Category-1 and Category-2(not shown here).

Fig.5.(a)Ensemble means ofand averaged in the KOE region in the ASO season for the warm events in Category-1(black bars)and in Category-2(gray bars).(b)As in(a)but for cold events.(c)Ensemble means of and averaged in the KOE region in the ASO season for the warm events in Category-1(black bars)and in Category-2(gray bars).(d)As in(c)but for cold events.(e)The differences inand between the warm(red bars)and cold(blue bars)events in Category-1 and Category-2 shown in(a–d).(f)As in(e)but for the term A= ?w?(ΔT)′and B= ?w′(ΔT)?.Units:K month?1.
Among all terms in Eqs.(5)–(6),only the physical processes ofandare directly related with the SSTA events to be predicted,and they respectively describe the effect of the prediction errors of the zonal,meridional and vertical oceanic temperature advection associated with the warm or cold events on the SSTA error growth.The u?,v?,w?and T?are respectively the anomalies of the zonal,meridional,vertical current velocities and SSTA in the North Pacific;and u′,v′,w′and T′represent their related prediction errors.A larger absolute value oforcauses a larger growth tendency(i.e.,growth rate)of prediction errors(i.e.,(?T′)/?t)and,as a result,leads to faster error growth.To investigate which of these terms contribute most to the larger error growth rates in the ASO season for the SSTA events in Category-1,the regional-meanorin the ASO season for the warm and cold events in Category-1(black bars)and Category-2(gray bars)are illustrated in Figs.5c and d. It is shown that only the,i.e.,the prediction errors of the vertical oceanic temperature advection associated with the SSTA events to be predicted,exhibits a significant difference between the two categories(as shown in Fig.5e),implying that the difference inis the major factor contributing the most to the large difference in error growth rates between the Category-1 and Category-2 events.In addition,a positive(negative)value of the processes on the right-hand side of Eq.(4)indicates the effect of favoring the error growth for warm(cold)events.Therefore,as shown in Figs.5c and d,a positive(negative)value offor the warm(cold)events in Category-1 causes error growth,while a negative(positive)value for the warm(cold)events in Category-2 suppresses error growth,which therefore leads to much larger error growth for the SSTA events in Category-1 than those in Category-2.
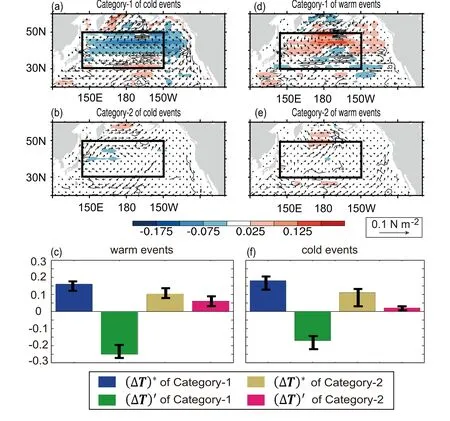
Fig.6.(a)The anomalous Ekman pumping(i.e.upwelling and down welling;contours;units:10?5m s?1)and wind stress anomalies(vectors;units:0.1 N m?2)in the ASO season for the warm events in Category-1.(b)As in(a)but for the warm events in Category-2.(c)The and in the ASO season for warm events(units:K m?1).(d–f)As in(a–c)but for the cold events.Color shading in(a,b)and(d,e)represents the 95%confidence level.The positive(negative)shaded values represent the upwelling(downwelling)of sea waters.The black rectangle marks the KOE-SSTA region(30°–50°N,145°E–150°W)which is the study area in this paper.
For warm events,the anomalous upwelling induced by the cyclonic wind stress anomalies over the KOE region for Category-1 is much more significant than for Category-2(Figs.6a and b).The positivewhich also shows a larger value for Category-1 than Category-2(blue bars and yellow bars in Fig.6c),implies that the anomalous upwelling brings the cold water to upper ocean layers and leads to the cooling of KOE-SSTA.Therefore,the more significant anomalous upwelling for Category-1 causes much more cooling of KOE-SSTA,which explains why the warm events in Category-1 transfer more rapidly from the mature to decaying phase than those in Category-2.Moreover,Fig.6c shows that the(ΔT)′=(T′?T)/h is negative with a large absolute value for Category-1(green bars).Therefore,for the warm events in Category-1,the significant upwelling(i.e.,a positive value of vertical velocity w?in term A)and a negativevalueoflead to a positive term A(i.e.,positive oceanic temperature advection errors by anomalous vertical currents of the SSTA events),and in turn cause a positive,which favors the rapid growth of warm prediction errors according to Eq.(5).Compared with Category-1,the error growth induced byis much weaker due to the negligible vertical advection for Category-2(Fig.6b).As shown inFig.5c,the large difference inenhances the difference in error growth rates between the SSTA events in Category-1 and Category-2,and therefore favors a greater possibility of a more significant SPB for the SSTA events in Category-1.The mechanisms are similar for the cold events(see Figs.6d–f).
Overall,the mature-to-decaying transition of SSTA and the growth of prediction errors in the ASO season are both related with the anomalous upwelling or down welling in the transition phase of the SSTA events to be predicted.The anomalous upwelling or down welling in the ASO season for the SSTA events in Category-1 is much more significant than in Category-2,which not only leads to the largest mature-to decaying transition rate of SSTA but also results in the fastest error growth for the SSTA events in Category-1.Therefore,this explains why the SSTA events transferring more rapidly from the mature to decaying phase tend to yield a greater possibility of a more significant SPB.
5.Summary and discussion
This paper investigates the impact of KOE-SSTA events on the SPB in the North Pacific by analyzing the results from two perfect model predictability experiments(Exp Reference and Exp Random).Thirty KOE-SSTA events are randomly selected as the reference states to be predicted,which can be classified into two categories:Category-1 transfers more rapidly from the mature to decaying phase,with a transition rate larger than 0.3 K month?1;and Category-2 has a relatively smaller rate.The KOE-SSTA events in both categories are predicted from different start months with Ref-type initial errors that have certain spatial patterns in Exp Reference,and with random initial errors in Exp Random.The results from both experiments show that the SPB usually occurs during the mature-to-decaying transition phase of the SSTA events to be predicted;and the SSTA events in Category-1,which transfer more rapidly from the mature to decaying phase,tend to yield a greater possibility of a more significant SPB than those events in Category-2.
The physical mechanisms responsible for the dependence of the SPB on the mature-to-decaying transition rates of SSTA events are explored.It is found that the SSTA events in Category-1 have larger wind stress curl anomalies over the KOE region during the ASO season than those events in Category-2.For the SSTA events in Category-1,the larger positive(negative)wind stress curl anomalies favor the larger anomalous upwelling(downwelling)of waters dynamically through the Ekman effect for warm(cold)events,which contributes most to the larger oceanic temperature advection errors by anomalous vertical currents of KOE-SSTA events,and in turn leads to the larger prediction errors of vertical oceanic temperature advection associated with SSTA events[i.e.,in Eq.(4)].Therefore,the large difference infavors the large difference in error growth rates in the ASO season between the Category-1 and Category-2 events.Ultimately,the SSTA events in Category-1 yield a greater possibility of a more significant SPB than those events in Category-2.Furthermore,a more significant anomalous upwelling(downwelling)in the ASO season favors much more SSTA cooling(warming),i.e.,the faster SSTA transition from the mature to decaying phase for the warm(cold)events in Category-1.That is,the mature-to-decaying transition rate of SSTA and the error growth rate in the ASO season are both related with the anomalous upwelling(down welling)induced by wind stress curl anomalies.Therefore,this explains why the SSTA events transferring more rapidly tend to yield a greater possibility of a more significant SPB.
In Fig.5,it should be noted that the ensemble mean errors associated with latent heat and vertical advection have the same sign as the KOE-SSTA to be predicted,which indicates overestimated SST A during the mature-to-decaying transition phase in predictions.Duan and Wu(2015)explained that the overestimated SSTA is caused by enhanced anticyclonic(cyclonic)wind stress error for warm(cold)events.Also,the enhanced anticyclonic(cyclonic)wind stress error is probably induced by the perturbed initial sea temperature fields in predictions.The results of Exp Random are analyzed with the same method as in Exp Reference,showing that the magnitudes ofandare much smaller than the results of Exp Reference(not shown here).This may imply that the Ref-type initial errors can cause more enhanced anticyclonic(cyclonic)wind stress errors and result in larger prediction errors ofandthan the random initial errors.However,how the sea temperature initial errors cause the anticyclonic(cyclonic)wind stress errors for warm(cold)events remains unclear and needs to be explored in future work.
The results presented in this paper suggest that the occurrence of the SPB is dependent on the evolutionary characteristics of the SSTA events to be predicted.The forecast skill may decline dramatically due to the significant error growth when predicting the SSTA events with large mature to-decaying transition rates.However,it is obvious that the transition rate of an SSTA event is unknown to us before it really happens in real-time forecasts.This matter of what can be considered as the indicator of the transition rate for the KOE-SSTA events should be addressed.It is demonstrated in section 4 that the cyclonic(anticyclonic)wind stresses in the transition phase are responsible for the SSTA transition for the warm(cold)events.Thus,it is interesting whether the sea surface wind stress is an indicator of the SSTA transition.In Figs.1c and d,it is shown that the anticyclonic wind stress anomalies favor the development of warm KOE-SSTA for both categories at leads of?4 and?2 months.However,for Category-1,the cyclonic wind stress anomalies appear after the peak,which therefore results in the fast decay of warm SSTA.For Category-2,the wind transformation from anticyclonic to cyclonic is much later,which therefore favors the persistence of warm SSTA.A similar feature of wind evolution also can be seen in observations(not shown here).Furthermore,we show the composite spatial patterns of the seasonal SSTA growth rate and the related growth rate of sea surface wind stress anomalies in the North Pacific for the warm events in the two categories(Fig.7).The results illustrate that the SST A transition from mature to decaying phase during the ASO season for the warm events in Category-1 is much more significant than in Category-2(negative shaded values indicate the SSTA decaying rates for warm events).In addition,the cyclonic wind stress tendency(i.e.,wind stress growth rate)in the KOE region appears in the developing phase[the May–June–July(MJJ)season]and becomes much stronger in the transition phase(the ASO season)for Category-1.However,Category-2 does not exhibit this feature.The results for cold events are similar,except for the anticyclonic wind stress tendency in the MJJ season(not shown here).Therefore,the cyclonic(anticyclonic)wind stress appearing in the developing phase may suggest a rapid transition of the warm(cold)KOE-SSTA events.That is,the warm(cold)KOESSTA events with cyclonic(anticyclonic)wind stress anomalies in the developing phase may exhibit a significant SPB phenomenon.However,why the evolution of wind stress anomalies between the two categories shows such a large difference is still unclear and further efforts should be addressed to explore this problem.

Fig.7.The seasonal composite of the SSTA growth rate(contours;units:K month?1)and sea surface wind stress growth rate(vectors;units:0.1 N m?2)of the warm events in(a)Category-1 and(b)Category-2.Color shading represents the 95%confidence level.The black rectangle marks the KOE-SSTA region(30°–50°N,145°E–150°W)which is the study area in this paper.
Furthermore,it is demonstrated that the SPB induced by randominitial errors is weaker than the initial errors with spa-tial patterns,such as the Ref-type initial errors in this study.This implies that the initial errors with certain spatial patterns may lead to more prediction uncertainties in the forecasts of North Pacific SSTA.Therefore,it is suggested that removing the initial errors with certain spatial patterns before the predictions may weaken or eliminate the SPB and improve the forecast skill of North Pacific SSTA.In fact,previous studies have demonstrated that the prediction errors caused by the two kinds of initial errors with certain spatial patterns are most likely to induce a spring prediction barrier for ENSO events(Duan et al.,2009;Yu et al.,2009),and removing these kinds of initial errors could reduce the prediction errors in ENSO forecasts(Yu et al.,2012).This encourages us to explore which kinds of initial errors with certain spatial patterns are most likely to induce an SPB of KOE-SSTA and whether the forecast skill can be improved when removing these initial errors in predictions.Furthermore,the initial perturbations in this paper are only superimposed on the North Pacific and there are no perturbations over the equatorial Pacific.The present analyses only consider the local atmosphere–ocean coupling process.It is known that ENSO has a strong influence on the seasonal changes over the ex-tratropical North Pacific.The impact of the tropical Pacific on the predictability of KOE SSTA is also an important issue to be explored.Therefore,further efforts relating to these problems need to be made in our future work.
Acknowledgements.The authors are grateful for the insightful comments and constructive suggestions provided by the anonymous reviewers.This work was jointly sponsored by the National Natural Science Foundation of China(Grant No.41376018),the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDA11010303),the China Meteorological Administration Special Public Welfare Research Fund(GYHY201506013),the Project for Development of Key Techniques in Meteorological Forecasting Operation(YBGJXM201705),and the Open Foundation of the LASG/IAP/CAS.
Cane,M.A.,1983:Oceanographicevents during El Ni?o.Science,222,1189–1195,https://doi.org/10.1126/science.222.4629.1189.
Chang,P.,and Coauthors,2006:Climate fluctuations of tropical coupled system-The role of ocean dynamics.J.Climate,19,5122–5174,https://doi.org/10.1175/JCLI3903.1.
Curtis,S.,and R.F.Adler,2003:Evolution of El Ni?oprecipitation relationships from satellites and gauges.J.Geophys.Res.,108,4153,https://doi.org/10.1029/2002JD 002690.
Dai,A.,and T.M.L.Wigley,2000:Global patterns of ENSO-induced precipitation.Geophys.Res.Lett.,27,1283–1286,https://doi.org/10.1029/1999GL011140.
de Boisséson,E.,V.Thierry,H.Mercier,and G.Caniaux,2010:Mixed layer heat budget in the Iceland Basin from Argo.J.Geophys.Res.,115(18),C10055,https://doi.org/10.1029/2010JC006283.
Duan,W.S.,and Y.J.Wu,2015:Season-dependent predictability and error growth dynamics of Pacific Decadal Oscillationrelated sea surface temperature anomalies.Climate Dyn.,44,1053–1072,https://doi.org/10.1007/s00382-014-2364-5.
Duan,W.S.,X.C.Liu,K.Y.Zhu,and M.Mu,2009:Exploring the initial errors that cause a significant“spring predictability barrier”for El Ni?o events.J.Geophys.Res.,114(C4),https://doi.org/10.1029/2008JC004925.
Feng,R.,W.S.Duan,and M.Mu,2014:The“winter predictability barrier”for IOD events and its error growth dynamics:Results from a fully coupled GCM.J.Geophys.Res.,119,8688–8708,https://doi.org/10.1002/2014JC10473.
Gan,B.L.,and L.X.Wu,2012:Modulation of atmospheric response to North Pacific SST anomalies under global warming:A statistical assessment.J.Climate,25,6554–6566,https://doi.org/10.1175/JCLI-D-11-00493.1.
Guemas,V.,F.J.Doblas-Reyes,F.Lienert,Y.Souffet,and H.Du,2012:Identifying the causes of the poor decadal climate prediction skill over the North Pacific.J.Geophys.Res.,117(D20),D20111,https://doi.org/10.1029/2012JD018004.
Jacob,R.L.,1997:Low frequency variability in a simulated atmosphere-ocean system.PhD dissertation,University of Wisconsin-Madison,155 pp.
Latif,M.,T.P.Barnett,M.A.Cane,M.Flügel,N.E.Graham,H.von Storch,J.-S.Xu,and S.E.Zebiak,1994:A review of ENSO prediction studies.Climate Dyn.,9,167–179,https://doi.org/10.1007/BF00208250.
Lau,K.-M.,and S.Yang,1996:The Asian monsoon and predictability of the tropical ocean-atmosphere system.Quart.J.Roy.Meteor.Soc.,122,945–957,https://doi.org/10.1002/qj.49712253208.
Luo,J.-J.,S.Masson,S.Behera,and T.Yamagata,2007:Experimental forecasts of the Indian Ocean dipole using a coupled OAGCM.J.Climate,20,2178–2190,https://doi.org/10.1175/JCLI4132.1.
McPhaden,M.J.,2003:Tropical Pacific Ocean heat content variations and ENSO persistence barriers.Geophys.Res.Lett.,30,1480,https://doi.org/10.1029/2003GL016872.
Motokawa,N.,N.Matsuo,and N.Iwasaka,2010:Dominant seasurface temperature anomaly patterns in summer over the North Pacific Ocean.Journal of Oceanography,66,581–590,https://doi.org/10.1007/s10872-010-0048-2.
Philander,S.G.H.,1983:El Ni?o southern oscillation phenomena.Nature,302,295–301,https://doi.org/10.1038/302295a0.
Schott,F.A.,S.P.Xie,and J.P.McCreary Jr.,2009:Indian Ocean circulation and climate variability.Rev.Geophys.,47,RG1002,https://doi.org/10.1029/2007RG000245.
Stewart,R.H,2008:Introduction to physical oceanography.[Available online at http://oceanworld.tamu.edu/resources/ocng textbook/PDFif les/book.pdf.]
Wang,H.,A.Kumar,W.Q.Wang,and Y.Xue,2012:Seasonality of the Pacific decadal oscillation.J.Climate,25(1),25–38,https://doi.org/10.1175/2011JCLI4092.1.
Webster,P.J.,and S.Yang,1992:Monsoon and ENSO:Selectively interactive systems.Quart.J.Roy.Meteor.Soc.,118,877–926,https://doi.org/10.1002/qj.49711850705.
Wen,C.H.,Y.Xue,and A.Kumar,2012:Seasonal Prediction of North Pacific SSTs and PDO in the NCEP CFS Hindcasts.J.Climate,25,5689–5710,https://doi.org/10.1175/JCLI-D-11-00556.1.
Wu,Y.J.,W.S.Duan,and X.Y.Rong,2016:Seasonal predictability of sea surface temperature anomalies over the Kuroshio-Oyashio Extension:Low in summer and high in winter.J.Geophys.Res.,121,6862–6873,https://doi.org/10.1002/2016 JC011887.
Yamagata,T.,S.K.Behera,J.-J.Luo,S.Masson,M.R.Jury,and S.A.Rao,2004:Coupled ocean-atmosphere variability in the tropical Indian Ocean.Earth’s Climate:The Ocean-Atmosphere Interaction,C.Wang et al.,Eds.,American Geophysical Union,147,189–211,https://doi.org/10.1029/147GM12.
Yang,Y.,S.-P.Xie,L.X.Wu,Y.Kosaka,N.-C.Lau,and G.A.Vecchi,2015:Seasonality and predictability of the Indian Ocean dipole mode:ENSO forcing and internal variability.J.Climate,28,8021–8036,https://doi.org/10.1175/JCLI-D-15-0078.1.
Yu,Y.S.,W.S.Duan,H.Xu,and M.Mu,2009:Dynamics of nonlinear error growth and season-dependent predictability of El Ni?o events in the Zebiak-Cane model.Quart.J.Roy.Meteor.Soc.,135,2146–2160,https://doi.org/10.1002/qj.526.
Yu,Y.S.,M.Mu,W.S.Duan,and T.T.Gong,2012:Contribution of the location and spatial pattern of initial error to uncertainties in El Ni?o predictions.J.Geophys.Res.,117,C06018,https://doi.org/10.1029/2011JC007758.
Zhao,X.,J.P.Li,and W.J.Zhang,2012:Summer persistence barrier of sea surface temperature anomalies in the central western North Pacific.Adv.Atmos.Sci.,29,1159–1173,https://doi.org/10.1007/s00376-012-1253-2.
 Advances in Atmospheric Sciences2018年4期
Advances in Atmospheric Sciences2018年4期
- Advances in Atmospheric Sciences的其它文章
- Report on IAMAS Activity since 2015 and the IAPSO-IAMAS-IAGA Scientific Assembly—Good Hope for Earth Sciences
- Asymmetric Relationship between the Meridional Displacement of the Asian Westerly Jet and the Silk Road Pattern
- Idealized Experiments for Optimizing Model Parameters Using a 4D-Variational Method in an Intermediate Coupled Model of ENSO
- Variations in High-frequency Oscillations of Tropical Cyclones over the Western North Pacific
- Large-scale Circulation Control of the Occurrence of Low-level Turbulence at Hong Kong International Airport
- Evaluating the Capabilities of Soil Enthalpy,Soil Moisture and Soil Temperature in Predicting Seasonal Precipitation
