蘇云飛,姚磊

(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)

1 引言

本文研究了二維空間中非齊次不可壓縮Navier-Stokes/Vlasov-Fokker-Planck方程組的漸近分析,這類方程組應(yīng)用在各種工業(yè)問(wèn)題中,如沉降問(wèn)題,廢水處理,化學(xué)工藝[1-3]等方面.一方面,從微觀的角度考慮,粒子的運(yùn)動(dòng)是由依賴于時(shí)間t∈[0,T],空間位置x∈T2,粒子的速度v∈R2的分布函數(shù)f(x,v,t)描述的,滿足Vlasov-Fokker-Planck方程：

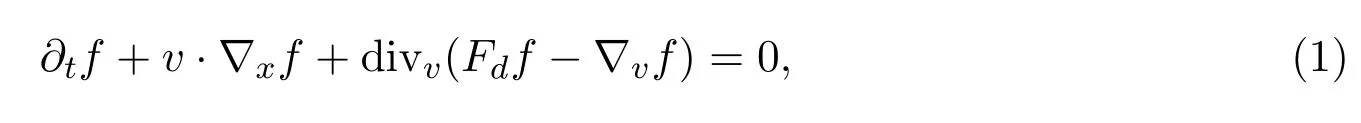
其中Fd=F0(u(x,t)?v),不失一般性令F0=1.

另一方面,流體是通過(guò)宏觀量描述,其中ρ(x,t)≥0是密度,u(x,t)∈R2是速度場(chǎng),這些量滿足非齊次不可壓縮Navier-Stokes方程

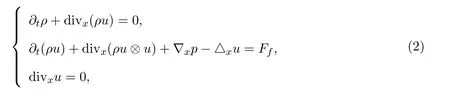
其中

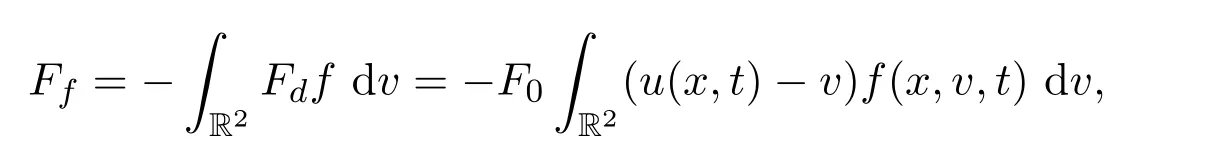
且假設(shè)壓力p=Aργ,不失一般性令A(yù)=1.

關(guān)于流體-粒子模型解的適定性問(wèn)題已被廣泛研究,許多學(xué)者研究了流體-粒子模型解的全局存在性結(jié)果.文獻(xiàn)[4]討論了在有界區(qū)域中,Vlasov-Stokes方程組弱解的全局存在性和大時(shí)間行為.其次,文獻(xiàn)[5]證明了在三維周期區(qū)域中,不可壓縮Navier-Stokes-Vlasov方程組弱解的整體性.文獻(xiàn)[6]討論了不可壓縮Navier-Stokes/Vlasov-Fokker-Planck方程組在二維空間和三維空間中弱解的全局存在性以及二維空間中光滑解的全局存在性和唯一性.接下來(lái),文獻(xiàn)[7-8]分別研究了三維有界區(qū)域中非齊次不可壓縮Navier-Stokes-Vlasov方程組和不可壓縮Navier-Stokes-Vlasov方程組弱解的全局存在性.在可壓縮的情況下,文獻(xiàn)[9]討論了在三維有界區(qū)域中可壓縮Navier-Stokes/Vlasov-Fokker-Planck方程組弱解的全局存在性.還有一些其它相關(guān)模型的解的存在性結(jié)果,讀者可以參看文獻(xiàn)[10-11].

本文主要研究下列方程組的漸近性(ε→0),

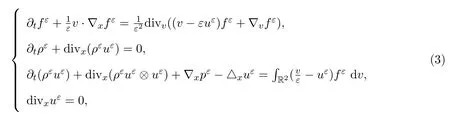
初始條件為:

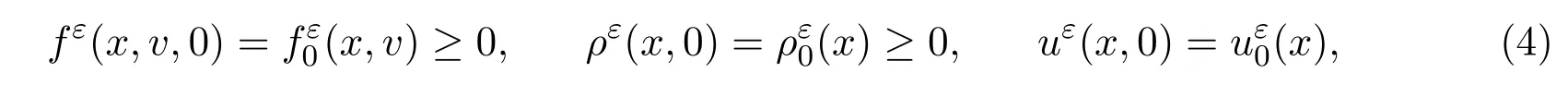
其中x∈T2表示空間變量,t∈[0,T]表示時(shí)間變量,v∈R2表示粒子的速度,pε表示壓力,且

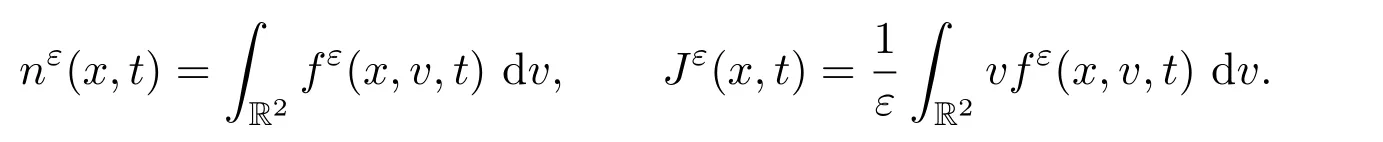
為了克服邊界條件的影響,這里討論二維周期區(qū)域T2.

近年來(lái),有許多關(guān)于流體 -粒子模型的流體動(dòng)力學(xué)極限的結(jié)果.對(duì)于一維的情形,文獻(xiàn)[12]討論了Vlasov方程與粘性Burgers方程耦合的方程組的動(dòng)力學(xué)極限和分層極限.在多維情況下,文獻(xiàn)[13]證明了在三維有界區(qū)域中可壓縮Navier-Stokes/Vlasov-Fokker-Planck方程組的流體動(dòng)力學(xué)極限結(jié)果.文獻(xiàn)[14-15]分別研究了在輕粒子和好粒子兩種情形下,不可縮Navier-Stokes/Vlasov-Fokker-Planck方程組的兩種流體動(dòng)力學(xué)極限.文獻(xiàn)[16]基于相對(duì)熵和弱緊性方法研究了Vlasov型方程的流體動(dòng)力學(xué)極限.關(guān)于其它相關(guān)模型的漸近分析研究,讀者可以參看文獻(xiàn)[17-18].

這篇論文主要是討論問(wèn)題(3)-問(wèn)題(4)的漸近極限,其極限解(n,ρ,u)滿足下列方程:

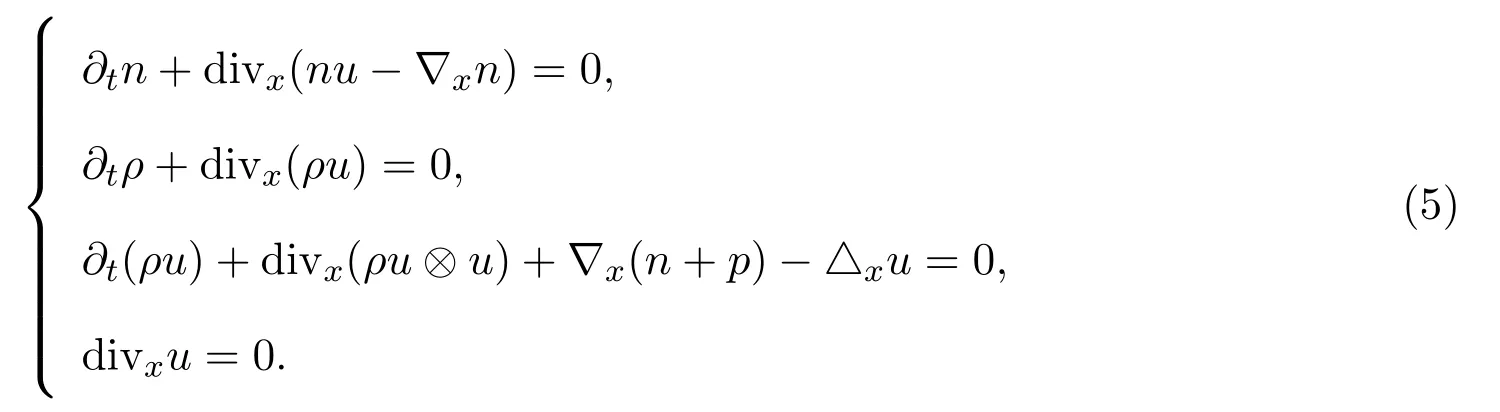
這篇文章的結(jié)構(gòu)安排如下:第二部分做能量估計(jì)并陳述文章的主要結(jié)果;第三部分得到一些與ε無(wú)關(guān)的一致估計(jì),并取極限,完成定理的證明.

2 主要結(jié)果

2.1 能量估計(jì)

首先,(3)1兩邊同時(shí)乘以再關(guān)于x和v求積分,得

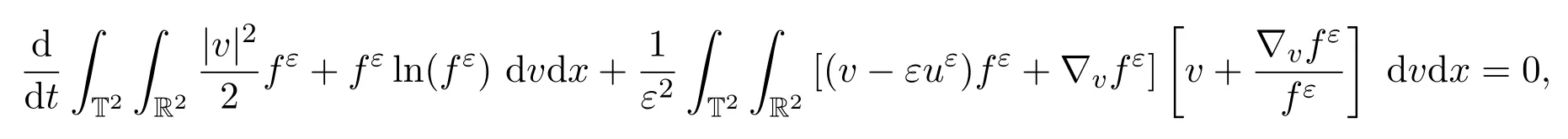
其次,(3)3兩邊同時(shí)乘以u(píng)ε,再關(guān)于x求積分,得

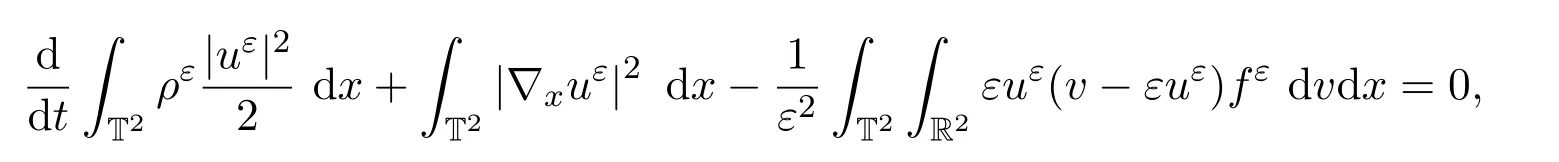
最后,結(jié)合上面兩個(gè)等式有:

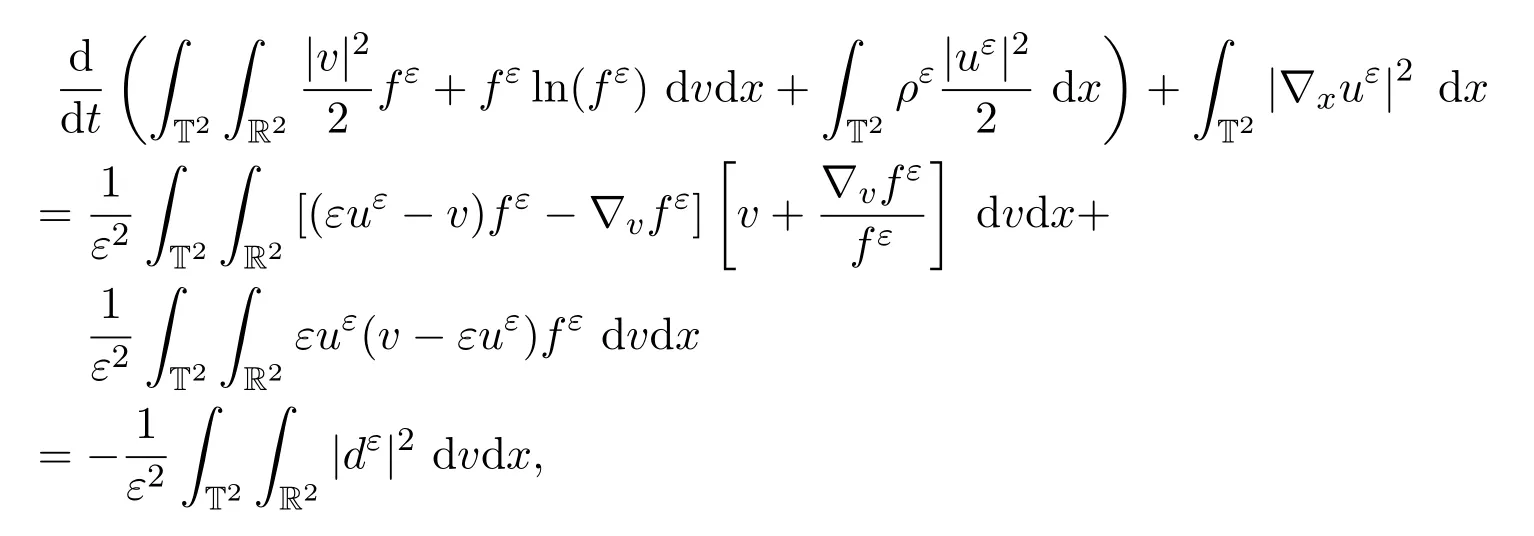
其中,令

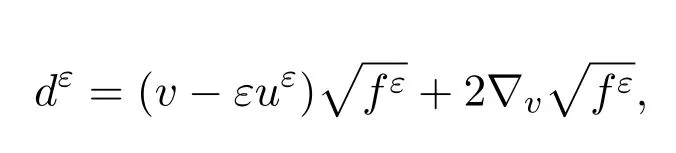
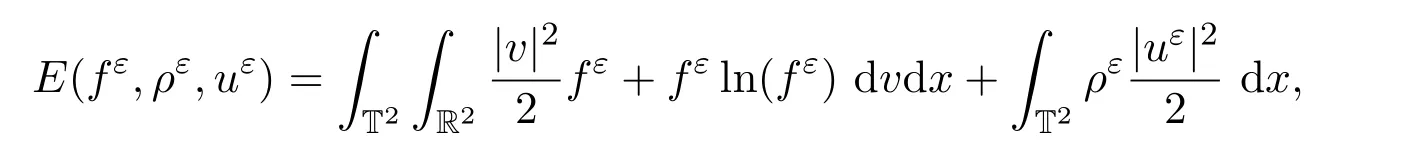
因此,將上式關(guān)于t積分可得

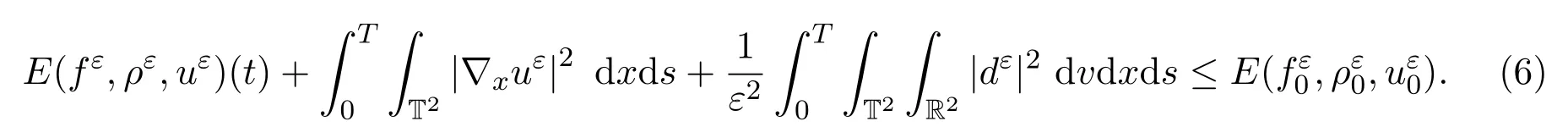
注 1.1關(guān)于二維空間非齊次不可壓縮Navier-Stokes/Vlasov-Fokker-Planck方程組弱解的全局存在性,結(jié)合文獻(xiàn)[4,19]可以得到.

2.2 主要結(jié)果

定理 2.1設(shè)初值滿足:

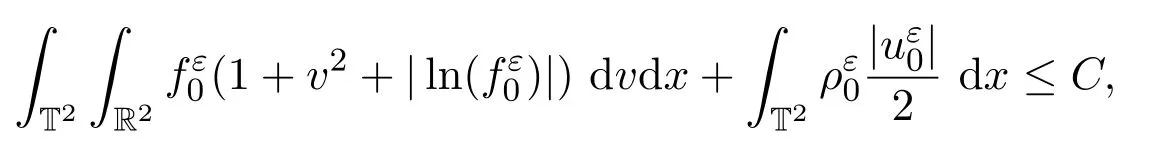
ρε0在L1(T2) 中收斂到ρ0.

那么,存在子列 (仍記為本身)使得下列收斂性成立:nε在中收斂到n,ρε在C([0,T];Lp(T2))中強(qiáng)收斂到在中強(qiáng)收斂到

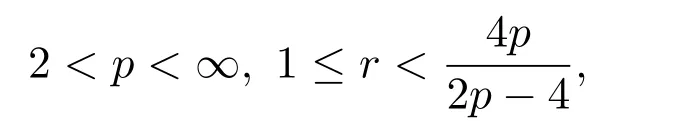
uε在Lθ(0,T;Lr(T2))中強(qiáng)收斂到u,其中 1≤θ＜2.這里 (n,ρ,u)滿足其中

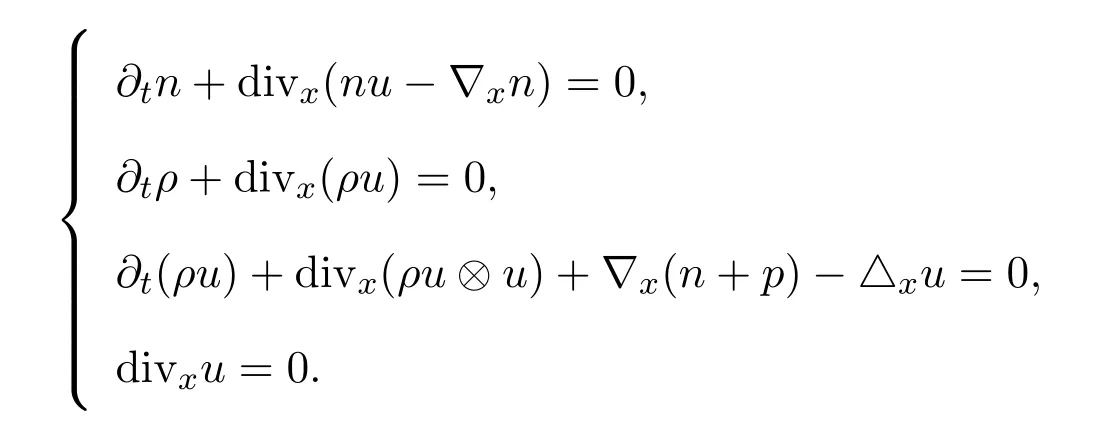
注 2.1定理2.1將文獻(xiàn)[14]的結(jié)果推廣到非齊次不可壓縮的情形.

3 定理2.1的證明

3.1 一致估計(jì)

命題 3.1在定理 2.1的假設(shè)前提下,設(shè)(fε,ρε,uε)是問(wèn)題 (3)-問(wèn)題 (4)的一個(gè)弱解,則下列估計(jì)成立:

(i)uε在L2(0,T;H1(T2))中有界;

(ii)fε(1+v2+|ln(fε)|)在L∞(0,T;L1(T2×R2))中有界;

證明首先,從能量估計(jì)(6)式可以得到(i)和(ii)中的第二項(xiàng)估計(jì)成立;其次,通過(guò)質(zhì)量守恒

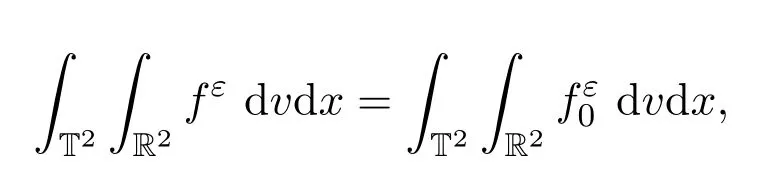
得到fε在L∞(0,T;L1(T2×R2))中有界.

接下來(lái),證明(ii)中的第三項(xiàng)估計(jì)成立.

引入

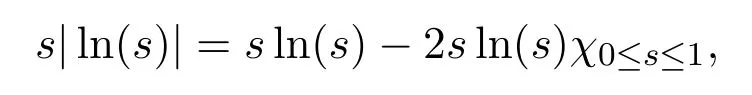
令ω≥0,那么

取s=fε,ω=v2/8,則有

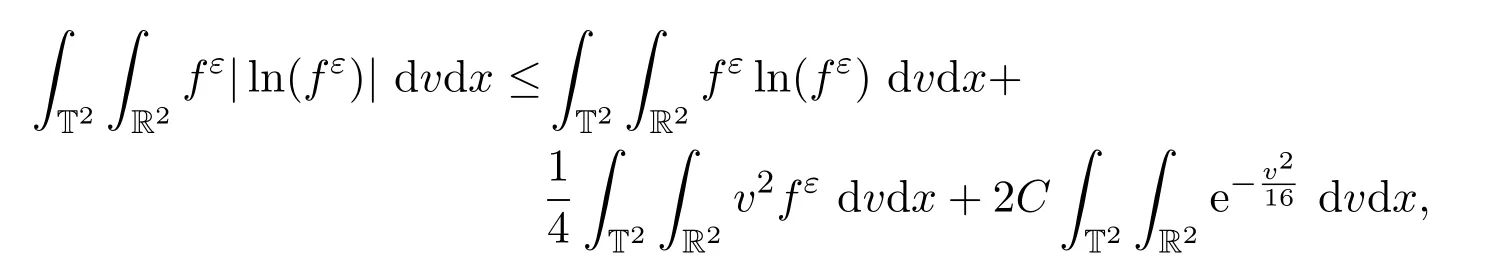
將此式與(6)式結(jié)合,可得

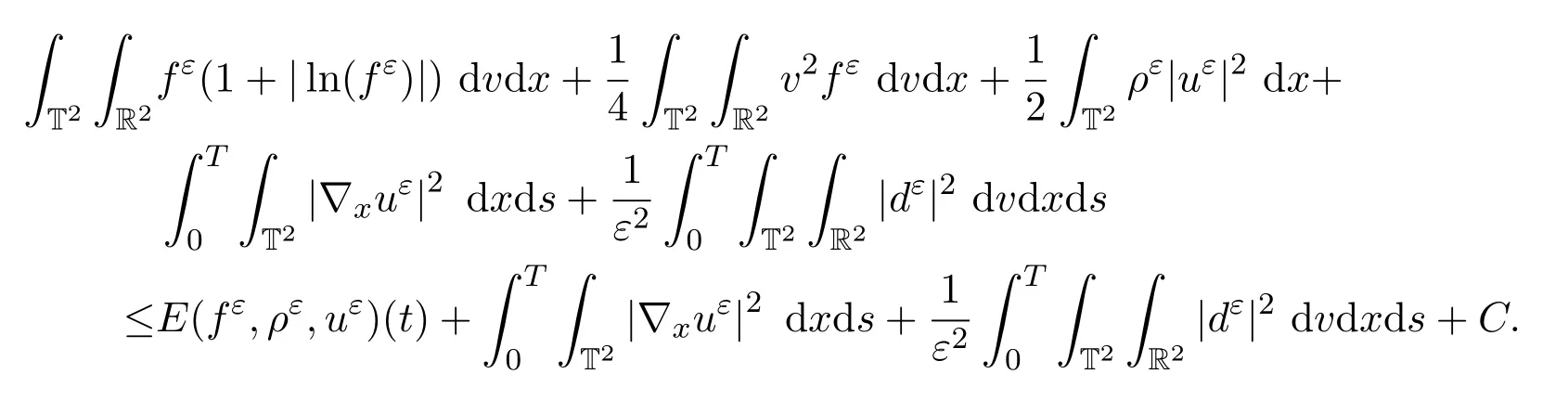
從而可以得出(ii)中的第三項(xiàng)成立.綜上,命題3.1得證.

其次,我們要對(duì)與微觀量fε相關(guān)的量做估計(jì).

命題 3.2在定理 2.1的假設(shè)前提下,設(shè) (fε,ρε,uε)是問(wèn)題 (3)-問(wèn)題 (4)的一個(gè)弱解,則下列估計(jì)成立:

(i)nε(1+|ln(nε)|)在L∞(0,T;L1(T2))中有界;

(ii)Jε?nεuε在L2(0,T;L1(T2))中有界.

證明首先,從命題3.1中的質(zhì)量守恒可得到nε在L∞(0,T;L1(T2))中有界.

其次,因?yàn)閔(s)=sln(s)是凸函數(shù),所以由Jensen不等式得

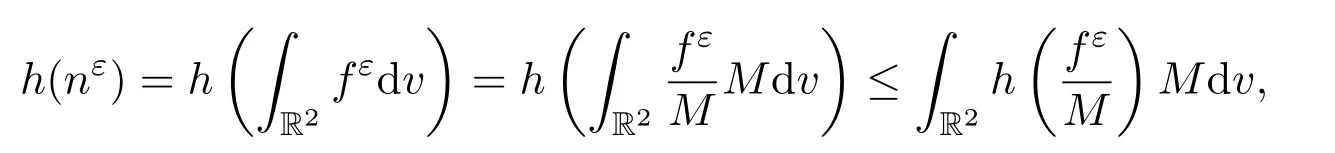
那么有

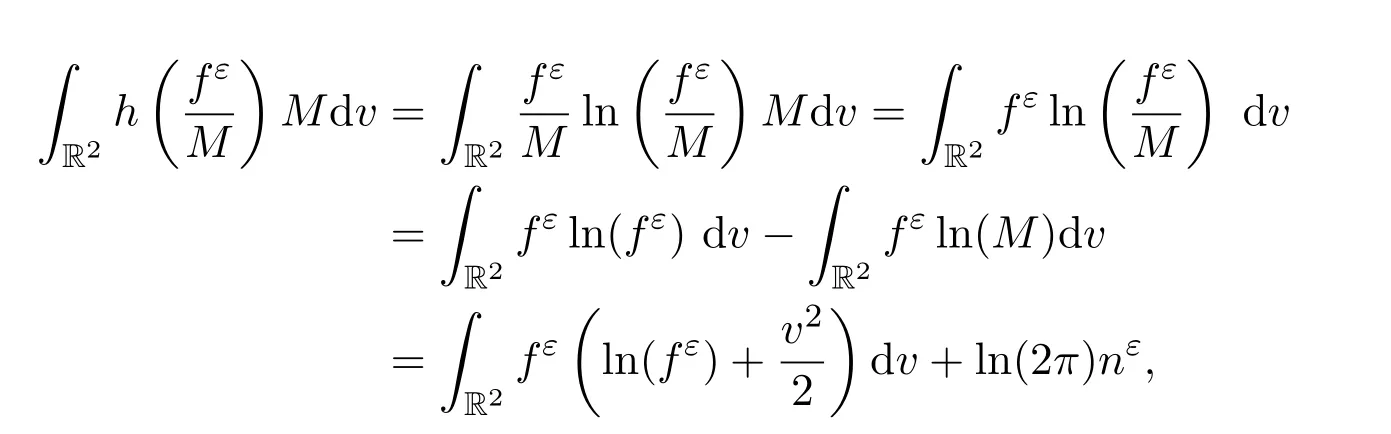
則有

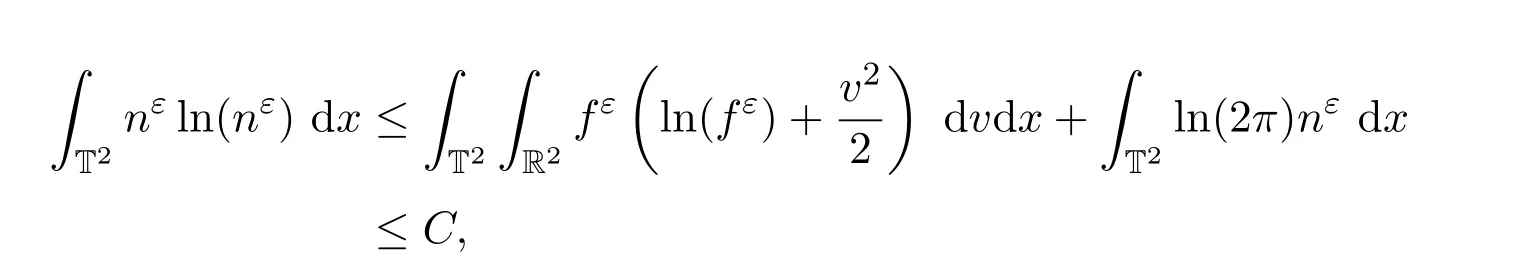
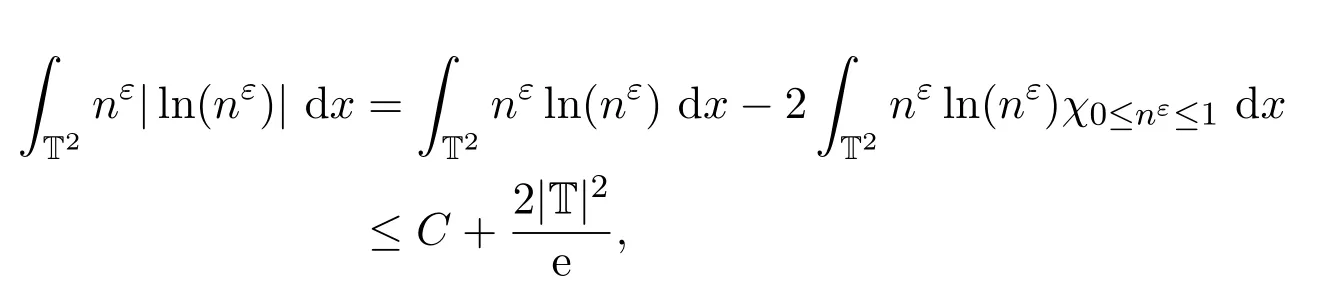
所以nε(1+|ln(nε)|)在L∞(0,T;L1(T2))中有界.

對(duì)于 (ii),有

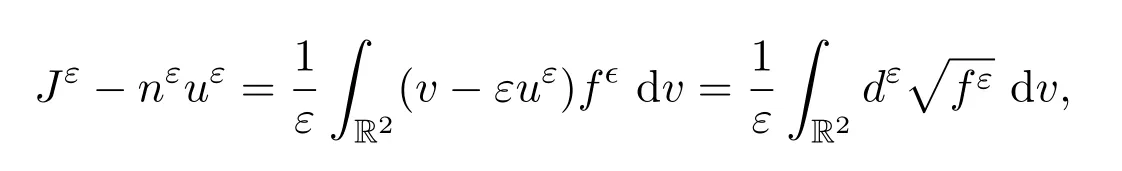
則

所以Jε?nεuε在L2(0,T;L1(T2))中有界.

為了證相關(guān)結(jié)論,需要用到二維空間的一個(gè)引理.

引理 3.1[14]設(shè)?是R2中的有界區(qū)域,Φ∈L2(0,T;H10(?)).設(shè)n≥0滿足

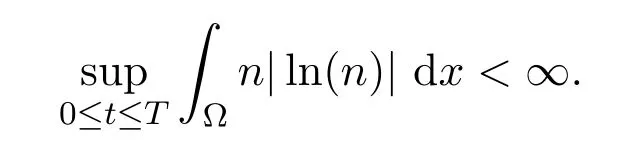
那么存在僅依賴于?的常數(shù)C,使得下列不等式成立

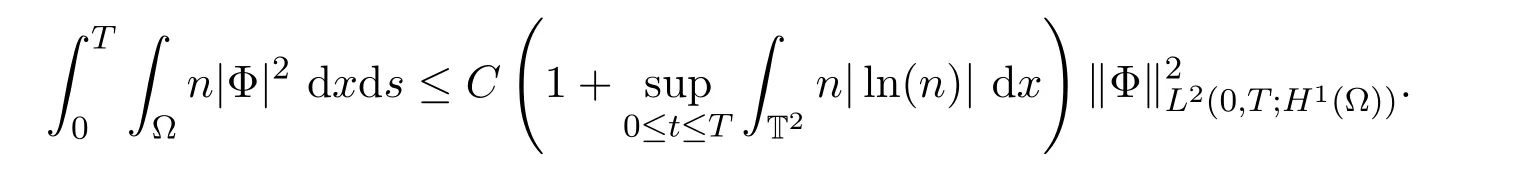
命題 3.3在定理 2.1的假設(shè)前提下,設(shè)(fε,ρε,uε)是問(wèn)題 (3)-問(wèn)題 (4)的一個(gè)弱解,則下列估計(jì)成立:

(ii)對(duì)任意的 0＜T＜∞,BR?T2,nεuε在L2(0,T;L1(BR))中有界.

證明利用引理3.1,對(duì)令則

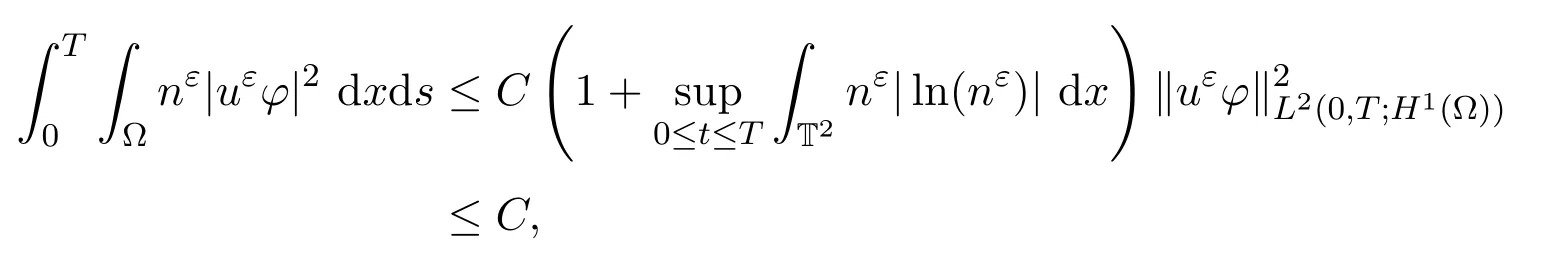
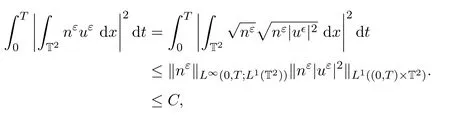
因此nεuε在L2(0,T;L1(BR))中有界.

最后,由于

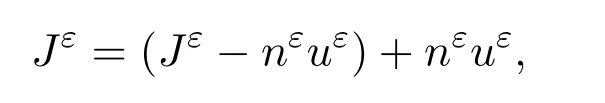
所以Jε在L2(0,T;L1(BR))有界.

為取ε→0的極限,還需要用到如下結(jié)論.

引理 3.2[19]設(shè)X是可分,自反的Banach空間,Y是Banach空間使得X嵌入到Y(jié),Y′是可分的,且在X′中稠密.假設(shè)gn滿足:對(duì)于1＜p≤∞時(shí),

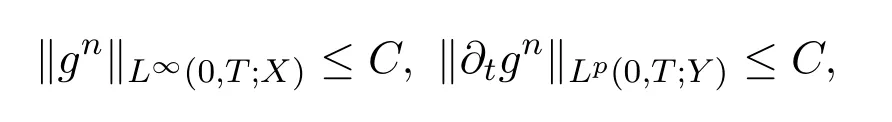
那么gn在C0([0,T];Xweak)中是相對(duì)緊的.

3.2 取極限

步驟 1極限方程的推導(dǎo).

由上述估計(jì),那么存在子列（記為本身）使得

(i)在L1((0,T)×T2)中,nε?n;

(ii)在D′((0,T)×T2)的意義下,Jε?J;

(iii)在L2(0,T;H1(T2))中,uε?u;

(iv)在L2((0,T)×T2)中,?xuε? ?xu;

(v)在D′((0,T)×T2)的意義下,

對(duì)于動(dòng)力學(xué)方程,首先,(3)1關(guān)于v求積分得

當(dāng)ε→0時(shí),在分布的意義下,

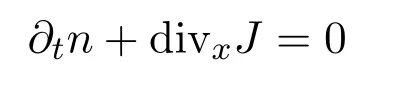
成立.由于nε在L∞(0,T;L1(T2))中有界,Jε在L2(0,T;L1(T2))中有界,利用(7)式可得?tnε在L2(0,T;W?1,1(T2))中有界,因此利用引理3.2的結(jié)論可得在中nε收斂到n.

給(3)1式兩邊同時(shí)乘以v,再關(guān)于v求積分,并利用分部積分得

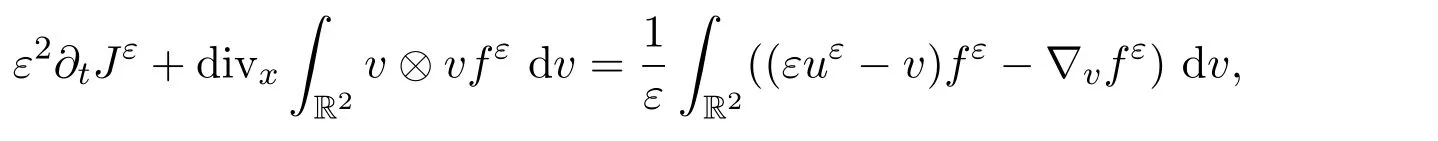
從而有

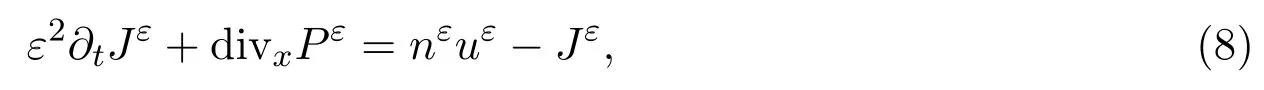
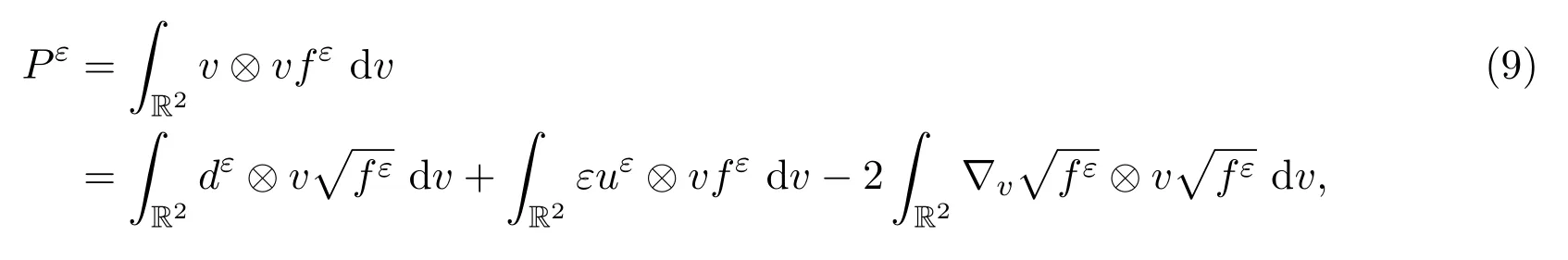
且

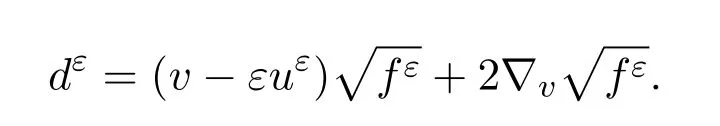
對(duì)(9)式的右邊第一項(xiàng)關(guān)于x,t求積分,結(jié)合Cauchy-Schwarz不等式,在關(guān)于ε一致有界的前提下,可以得出被O(ε)控制.右邊第二項(xiàng)在分布的意義下趨于0,即對(duì)任意的有

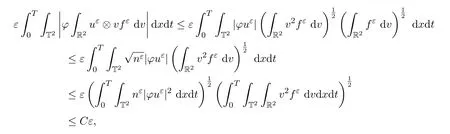
且第三項(xiàng)是nεI,從而在分布的意義下:

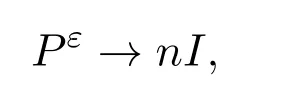
于是當(dāng)ε→0時(shí),有

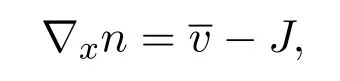
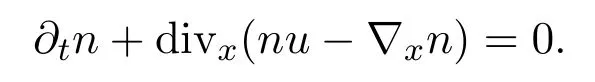
對(duì)于流體方程,由上述得到在分布的意義下,?xn是nεuε?Jε的極限(ε→0),如果進(jìn)一步可得到ρε,uε的強(qiáng)收斂,則有

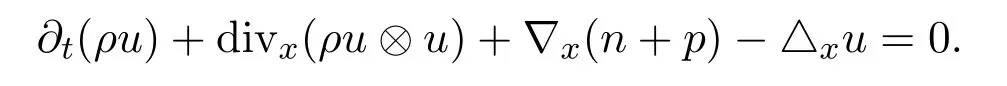
于是得到下列極限問(wèn)題滿足的方程組:

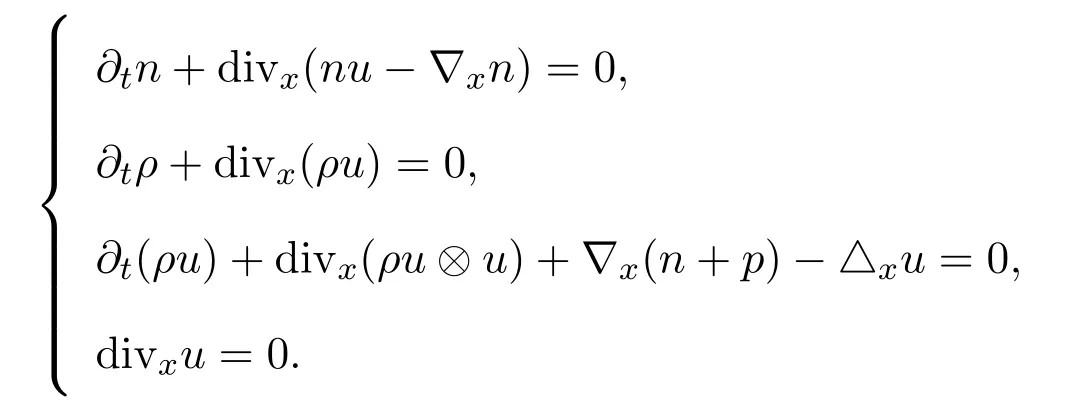
步驟 2證明ρε,uε的強(qiáng)收斂性.

首先,方程(3)2關(guān)于x求積分得

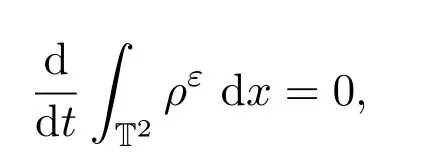
則

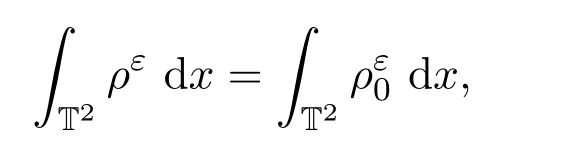
從而ρε在C([0,T];L1(BR))(?R∈(0,∞))中有界,且由能量不等式可得uε在L2(0,T;H1(T2))中有界.

接著,引入特征線X(s;x,t),滿足

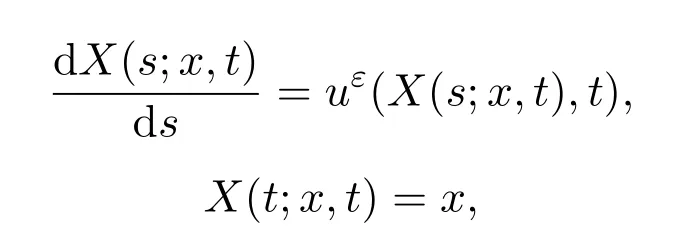
則

從而

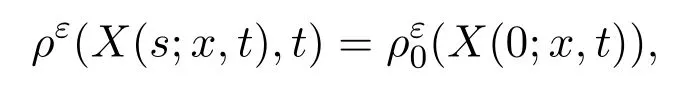
所以由假設(shè)

(a)0＜C1≤ ρε0≤C2,有C1≤ ρε≤C2;

(b)另外,在 T2×(0,T)上,幾乎處處成立,

(c)在分布的意義下,

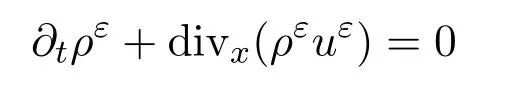
成立;

(d)在L1(T2)中,在L2(0,T;H1(T2))中,

由 (a),ρε0在Lp(T2))(1≤ p＜ ∞)中收斂到ρ0,且由 (b)可得,在 T2×(0,T)上,divxuε=0幾乎處處成立.

其次,由能量不等式可得ρε|uε|2在L∞(0,T;L1(T2))中有界,由 (a)可得ρε是一致有界的,則

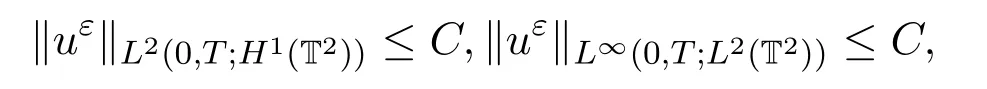
那么ρεuε?uε在中有界,這表明在中有界.

另外,△xuε在L2(0,T;H?1(T2))中有界.利用命題 3.2有Jε?nεuε在

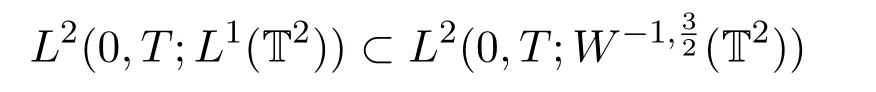
中有界.

因此,?t(ρεuε) 在中有界.進(jìn)一步,對(duì)任意的且 divφ=0,有

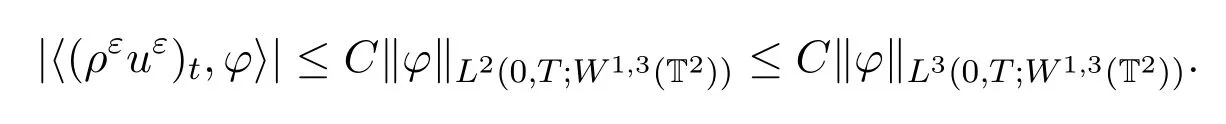
應(yīng)用文獻(xiàn)[20]中的定理2.4得到下列收斂:

(i)ρε(或)在C([0,T];Lp(T2))(1≤p＜ ∞)中強(qiáng)收斂到

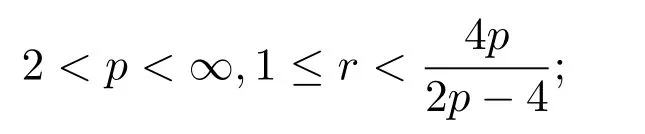
(iii)uε在Lθ(0,T;Lr(T2))中強(qiáng)收斂到u,其中1≤θ＜2,1≤r＜∞,ρ≥C1.

步驟3 證明其中

在分布的意義下,nεuε弱收斂到那么只需證明下面的引理,再利用極限的唯一性,則可以說(shuō)明

引理 3.3在分布的意義下,nεuε收斂到nu,即v=nu.

證明首先,由命題3.2可得nε|ln(nε)|在L∞(0,∞;L1(T2))中有界.對(duì)有

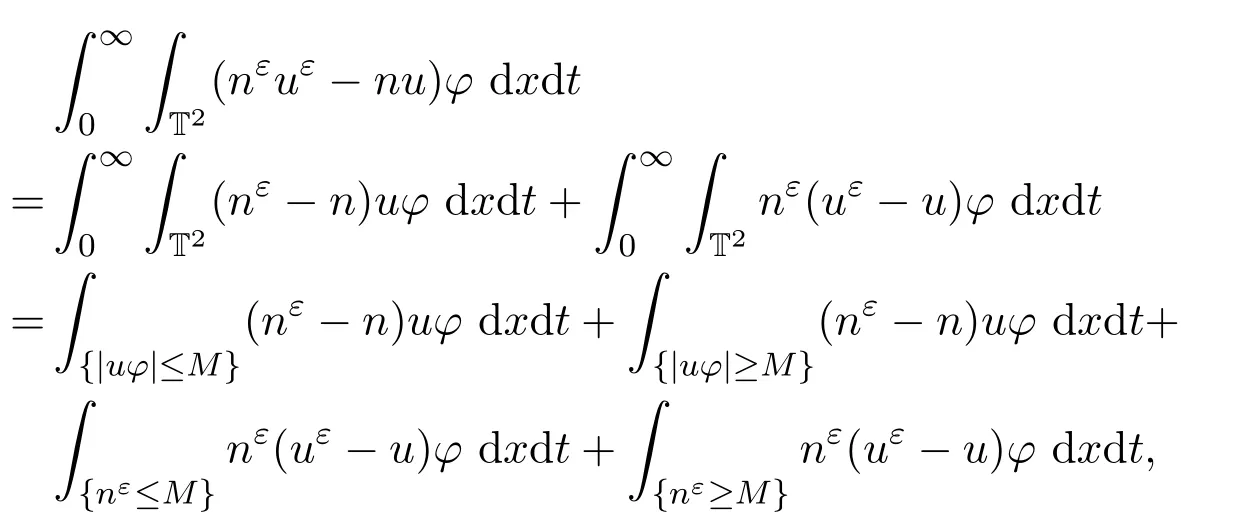
由于nε在L1((0,T)×T2)中弱收斂到n,所以有

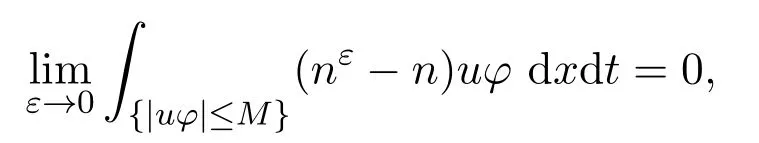
同理,利用uε在Lθ(0,T;Lr(T2))中強(qiáng)收斂到u,可得

其中θ′和r′分別為θ和r的共軛指標(biāo).

若能夠進(jìn)一步證明

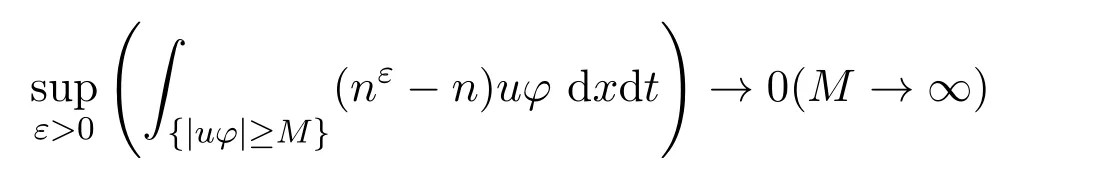
和

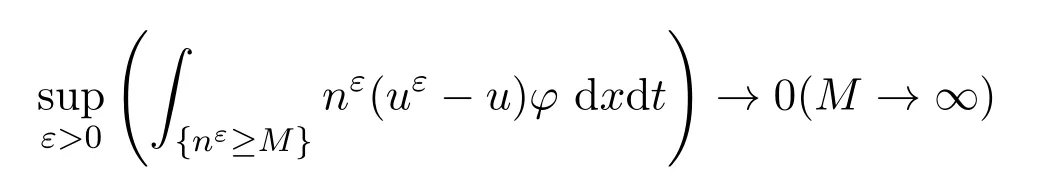
成立,則完成證明.首先,

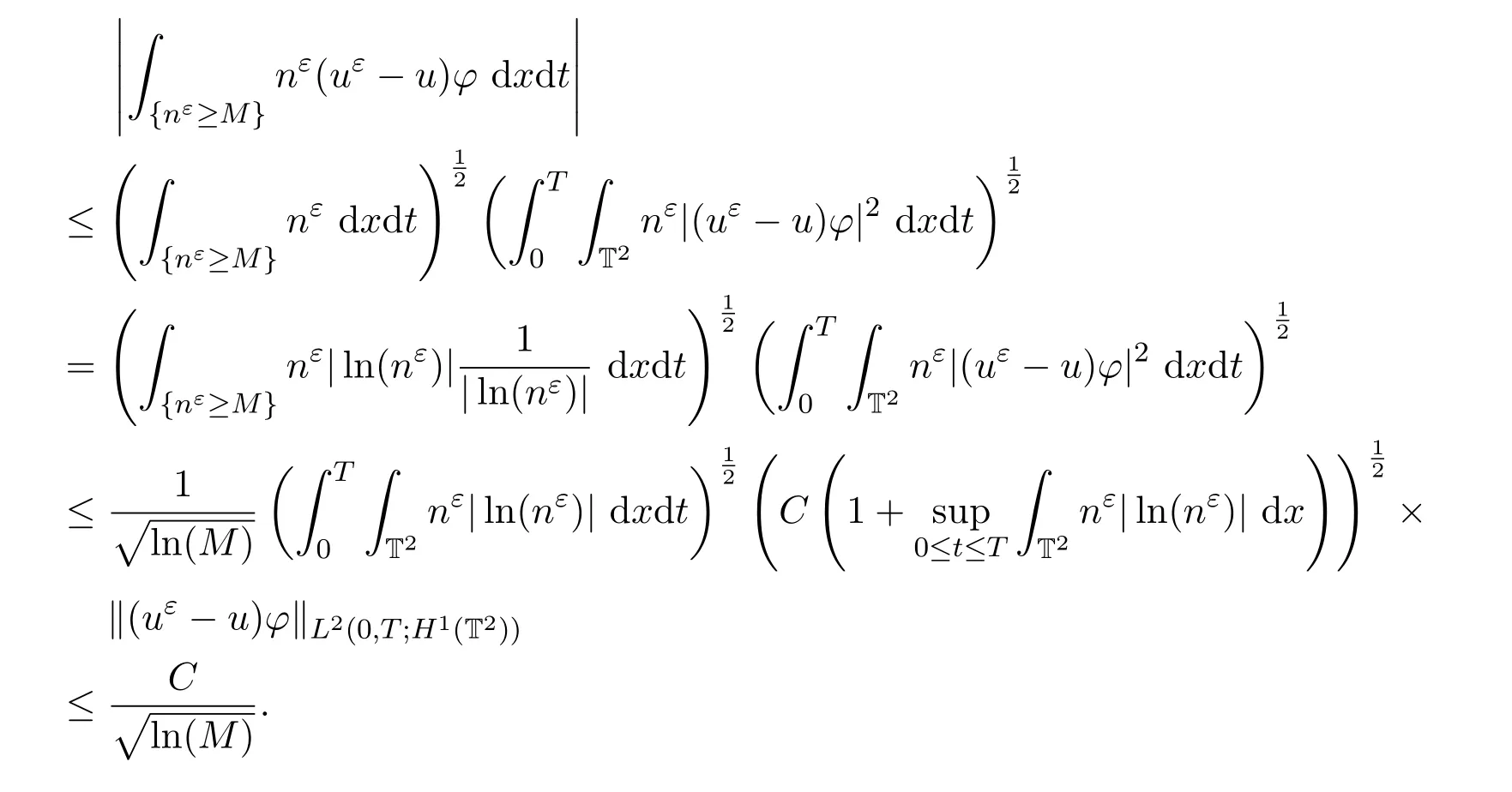
其次,

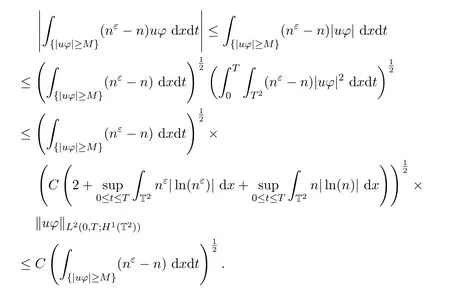
然而,當(dāng)M →0時(shí),meas({|uφ|＞M})→0.所以由 Dunford-Pettis定理,nε和n的等度可積性,可得

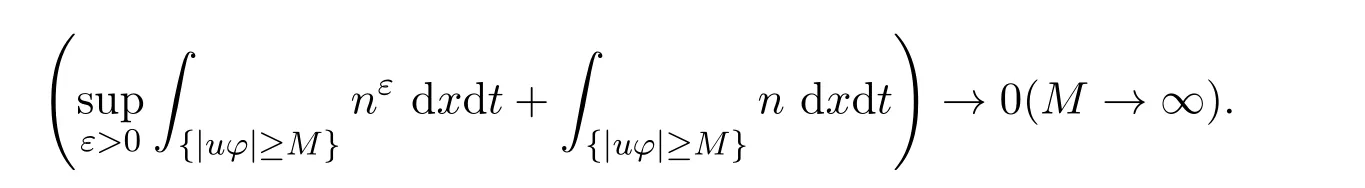
[1]Caflisch R,Papanicolaou G C.Dynamic theory of suspensions with Brownian effects[J].SIAM J.Appl.Math.,1983,43(4):885-906.

[2]Sartory W K.Three-component analysis of blood sedimentation by the method of characteristics[J].Math.Biosci.,1997,33(1/2):145-165.

[3]Williams F A.Spray Combustion and Atomization[J].Phys.of Fluids,1958,6(1):541-555.

[4]Hamdache K.Global existence and large time behaviour of solutions for the Vlasov-Stokes equations[J].Janpan J.Indust.Appl.Math.,1998,15(1):51-74.

[5]Boudin L,Desvillettes L.Grandmont C,et al.Global existence of solutions for the coupled Vlasov and Navier-Stokes equations[J].Differential Integral Equations,2009,22(11/12):1247-1271.

[6]Chae M,Kang K,Lee J.Global existence of weak and classical solutions for the Navier-Stokes-Vlasov-Fokker-Planck equations[J].J.Differential Equations,2011,251(9):2431-2465.

[7]Wang D H,Yu C.Global weak solution to the inhomogeneous Navier-Stokes-Vlasov equations[J].J.Differential Equations,2015,259(8):3976-4008.

[8]Yu C.Global weak solutions to the incompressible Navier-Stokes-Vlasov equations[J].J.Math.Pures Appl.,2013,100(2):275-293.

[9]Mellet A,Vasseur A.Global weak solutions for a Vlasov-Fokker-Planck/Navier-Stokes system of equations[J].Math.Models Methods Appl.Sci.,2007,17(7):1039-1063.

[10]Baranger C,Desvillettes L.Coupling Euler and Vlasov equations in the context of sprays:the local-in-time,classical solutions[J].J.Hyperbolic Differ.Equ.,2006,3(1):1-26.

[11]Carrillo J A,Choi Y P,Karper T K.On the analysis of a coupled kinetic-fluid model with local alignment forces[J].Ann.Inst.H.Poincaré Anal.NonLinéaire,2016,33(2):273-307.

[12]Goudon T.Asymptotic problems for a kinetic model of two-phase flow[J].Proc.Roy.Soc.Edinburgh Sect.A,2001,131(6):1371-1384.

[13]Mellet A,Vasseur A.Asymptotic analysis for a Vlasov-Fokker-Planck/compressive Navier-Stokes system of equations[J].Comm.Math.Phys.,2008,281(3):573-596.

[14]Goudon T,Jabin P E,Vasseur A.Hydrodynamic limit for the Vlasov-Navier-Stokes equations.I.Light particles regime[J].Indiana Univ.Math.J.,2004,53(6):1495-1515.

[15]Goudon T,Jabin P E,Vasseur A.Hydrodynamic limit for the Vlasov-Navier-Stokes equations.II.Fine particles regime[J].Indiana Univ.Math.J.,2004,53(6):1517-1536.

[16]Kang M J,Vasseur A.Asymptotic analysis of Vlasov-type equations under strong local alignment regime[J].Math.Models Methods Appl.Sci.,2015,25(11):2153-2173.

[17]Figalli A,Kang M J.A rigorous derivation from the kinetic Cucker-Smale model to the pressureless Euler system with nonlocal alignment[J].arxiv:1702.08087,2017.

[18]Karper T K,Mellet A,Trivisa K.Hydrodynamic limit of the kinetic Cucker-Smale flocking model[J].Math.Models Methods Appl.Sci.,2015,25(1):131-163.

[19]Lions P L.Mathematical Topics in Fluid Mechanics,Vol.II.Compressible Models[M].Oxford Lecture Series in Mathematics and its Applications.New York:The Clarendon Press,1998.

[20]Lions P L.Mathematical Topics in Fluid Mechanics,Vol.I.Incompressible Models[M].Oxford Lecture Series in Mathematics and its Applications.New York:The Clarendon Press,1996.