牛瀟萌,李書海

(赤峰學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,內(nèi)蒙古 赤峰 024000)

1 引言

設(shè)S表示在單位圓盤U={z:|z|＜1}內(nèi)單葉解析函數(shù)

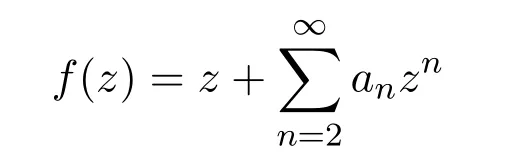
構(gòu)成的函數(shù)類.S?,C和Bα分別表示通常的星象函數(shù)類,近于凸函數(shù)類和 Bazileviˇc函數(shù)類,它們都是S的子類且S??C?Bα.

定義 1.1[1]設(shè)函數(shù)f(z)與g(z)在U內(nèi)解析,如果存在U內(nèi)Schwarz函數(shù)ω(z),滿足:

使得

則稱f(z)從屬于g(z),記作f(z)?g(z).特別地,如果g(z)在U上是單葉的,則

用P表示在U內(nèi)解析并且滿足條件:

的所有函數(shù)

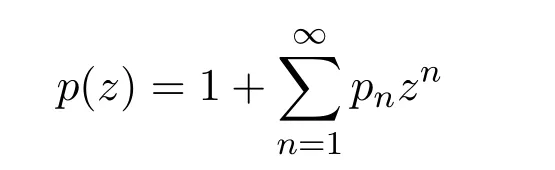
的全體.即P為正實(shí)部函數(shù)類.

設(shè)f(z)∈S,

其級數(shù)中相鄰兩系數(shù)模之差||Dn+1(λ)|?|Dn(λ)||的估計(jì)是單葉函數(shù)論中的一個(gè)重要問題.對于f∈S的形式,還尚未完全解決,而且對于相鄰兩系數(shù)模之差的精確估計(jì),在整個(gè)族中要辦到,是一個(gè)很困難的課題.

1946年,Goluzin首先發(fā)現(xiàn)了單葉函數(shù)相鄰系數(shù)相互制約的奇特性質(zhì),并證明了

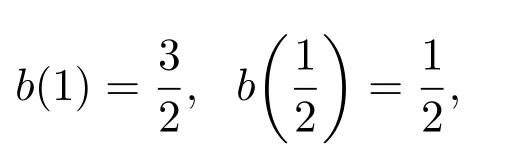
這引起了國內(nèi)外許多學(xué)者的興趣.近年來許多學(xué)者主要研究單葉函數(shù)中一些特殊函數(shù)族的相鄰系數(shù)模之差的估計(jì)[2-8].

本文研究如下由Al-Amiri和Fernando給出的復(fù)階近于凸函數(shù)類C(b)(見文獻(xiàn)[9]).

定義 1.2設(shè)f(z)∈S,b為復(fù)數(shù)且b≠0,如果存在g(z)∈S?,使得

則稱f(z)屬于復(fù)階近于凸函數(shù)類C(b).

Al-Amiri和Fernando在文獻(xiàn)[9]中給出了復(fù)階近于凸函數(shù)類C(b)的系數(shù)估計(jì)和偏差定理.Caglar在文獻(xiàn)[10]中給出了復(fù)階近于凸函數(shù)類C(b)的對數(shù)系數(shù),但是其相鄰兩系數(shù)模之差還沒有研究.本文研究了復(fù)階近于凸函數(shù)的相鄰兩系數(shù)模之差的估計(jì).

2 主要結(jié)果

為方便,函數(shù)f(z)的冪級數(shù)展開式中zn的系數(shù)an表示為an={f}n.

引理 2.1[9]設(shè)f(z)∈C(b),則對|z|=r＜1和|2b?1|≤1,有

引理 2.2[4]設(shè)f(z)∈S,G1(z)=(1?z)f(z)λ?1f′(z)z1?λ,0＜ λ ＜1,則對n≥2有

(1)

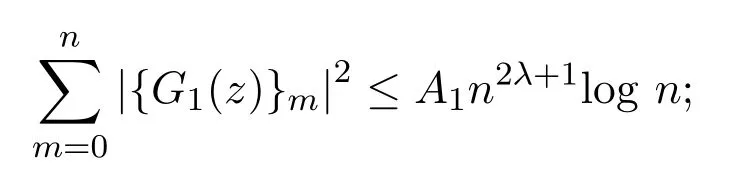
(2)

(3)

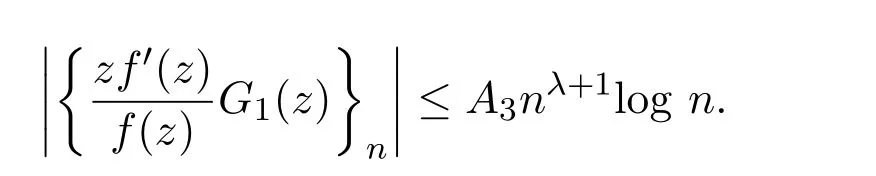
引理 2.3設(shè)f(z)∈C(b),g(z)∈S?滿足:

令

則對

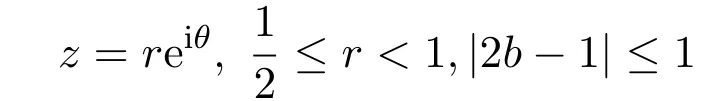
有

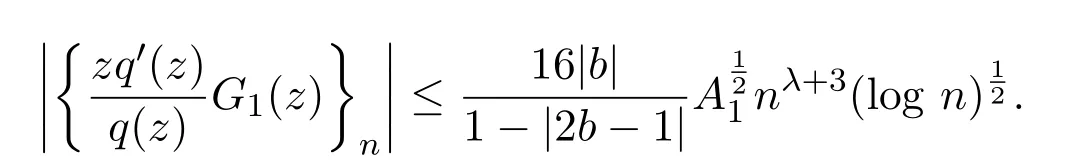
證明令

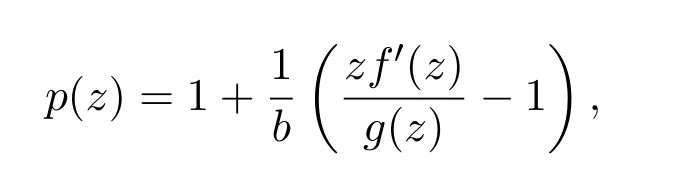
則p(z)∈P,由定義 1.1可知,存在解析函數(shù)ω(z),|ω(z)|＜1,ω(0)=0,使得

所以

由 Schwarz引理,可知

因此,對z=reiθ,有

由引理2.1,可知

從而

所以

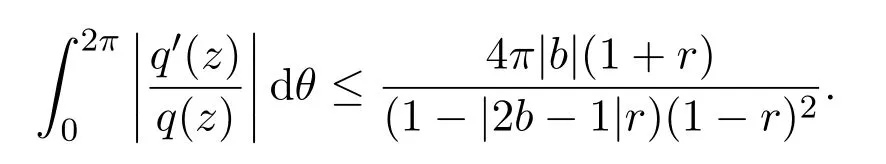
所以對z=reiθ,有

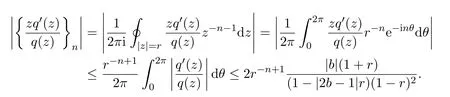
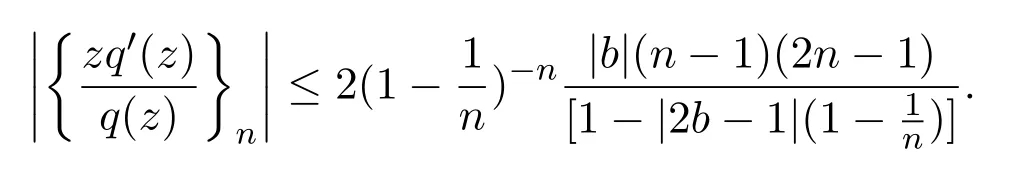
因?yàn)楫?dāng)n≥2時(shí)有,所以

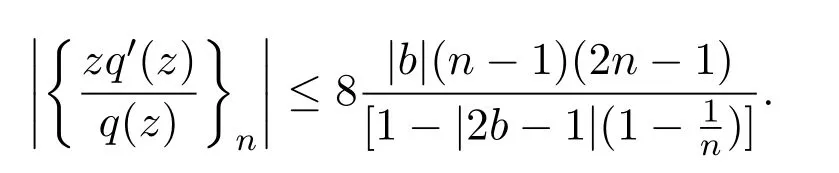
由Schwarz不等式,可知,

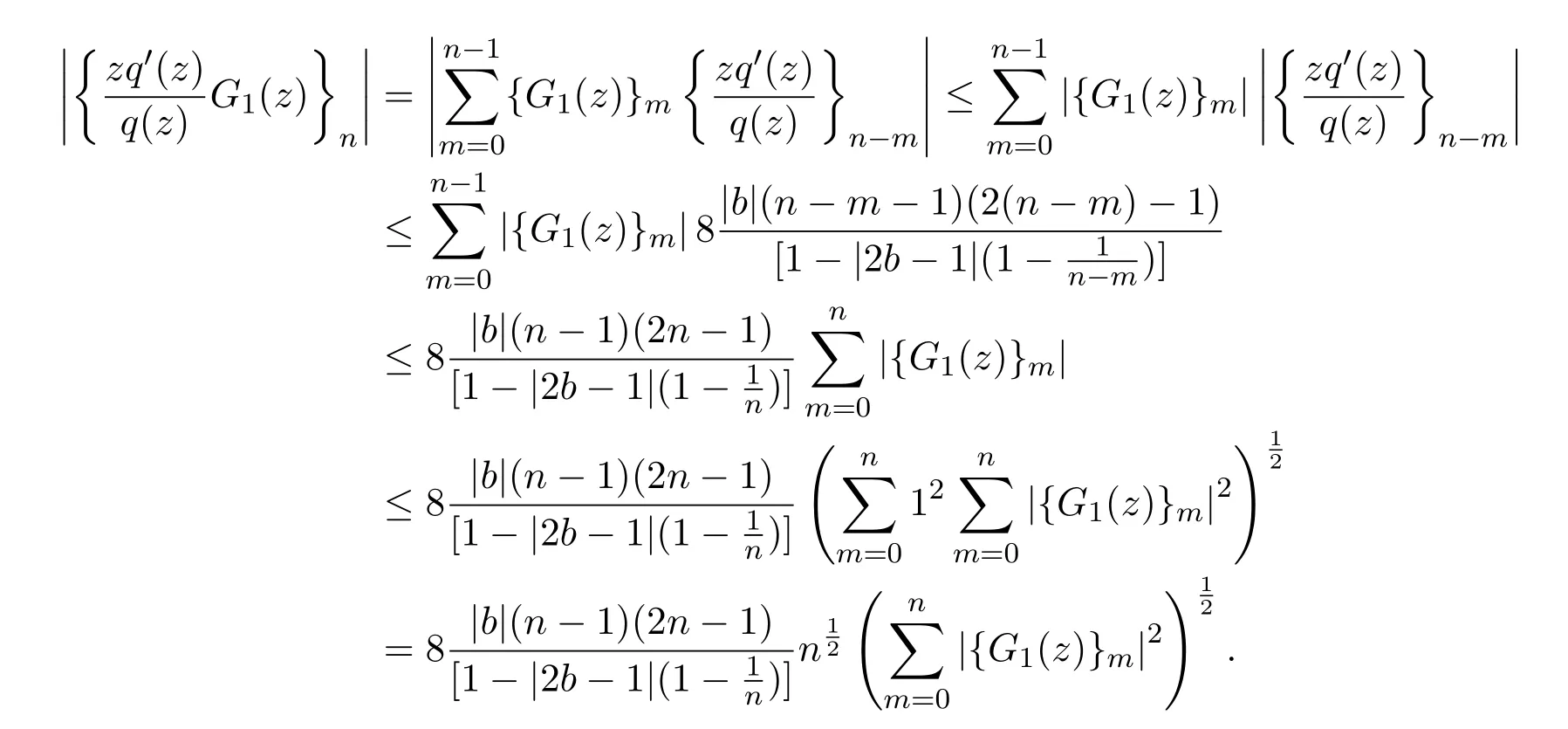
由引理2.2,可知

引理 2.4設(shè)f(z)∈ C(b),G1(z)=(1?z)f(z)λ?1f′(z)z1?λ,0＜ λ ＜1,則

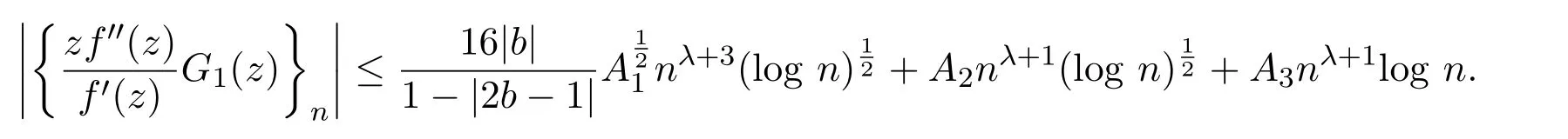
證明設(shè)f(z)∈C(b),則存在g(z)∈S?使得

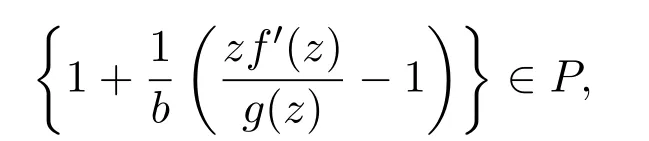
令

易知

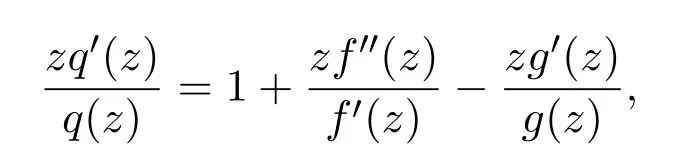
從而

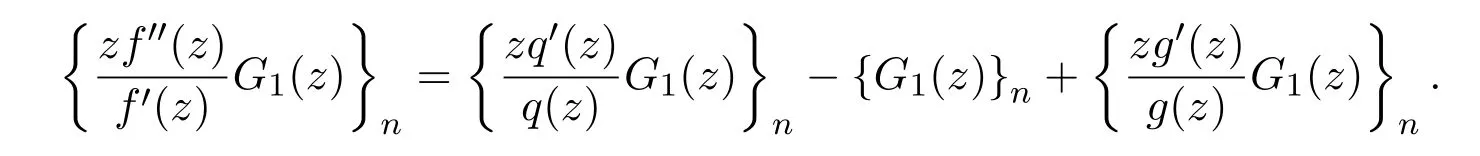
所以

由引理2.2和引理2.3,可知

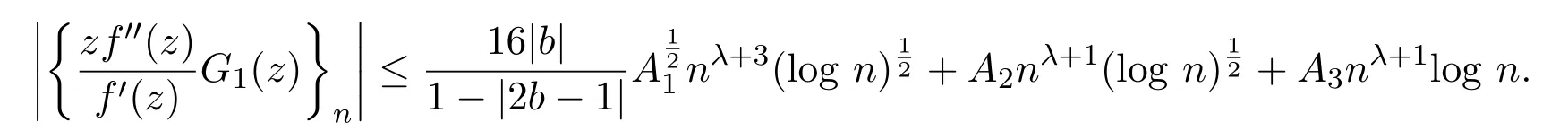
引理 2.5[4]設(shè)f(z)∈S,

則

引理 2.6[4]設(shè)f(z)∈S,ψ(z)由 (2)式定義,則

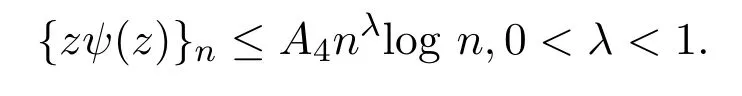
定理 2.1設(shè)f(z)∈C(b),Dn(λ)由(1)式定義,則對n≥2有

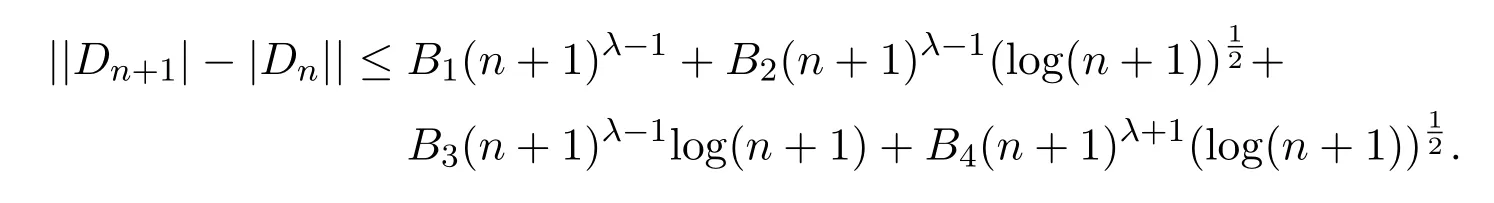
其中

是絕對常數(shù).

證明由(1)式易知

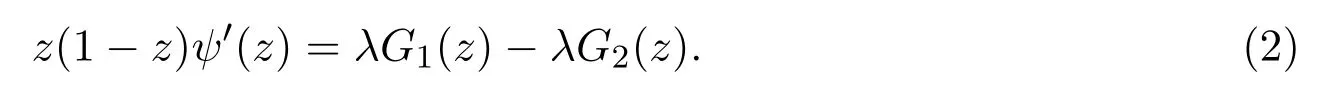
其中

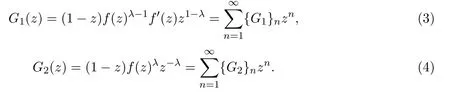
因?yàn)?/p>

所以

因?yàn)?/p>

所以由Schwarz不等式可知,

由引理2.2可知

所以由(3)式,引理2.2和引理2.4,可知

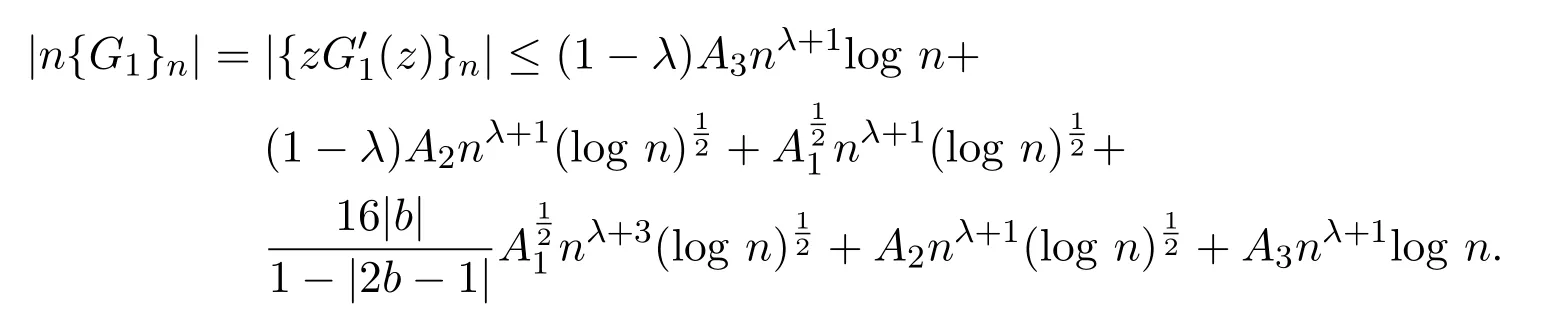
即

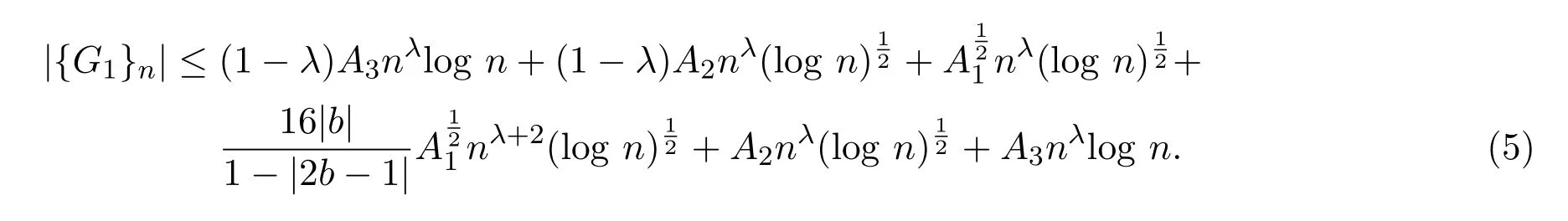
由引理2.5,可知

由 (2)式(5)式和 (6)式可知

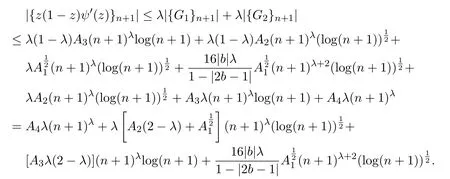
由(1)式,經(jīng)簡單計(jì)算可知,

所以

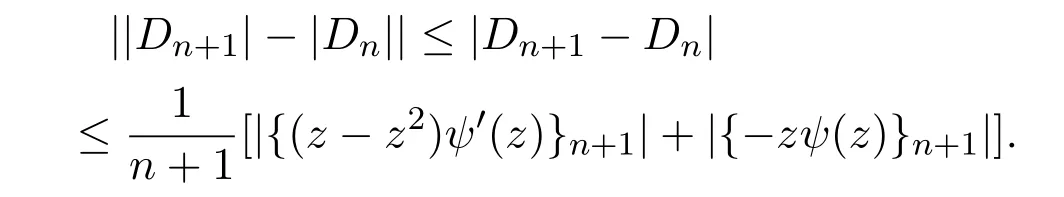
由引理2.6,可知

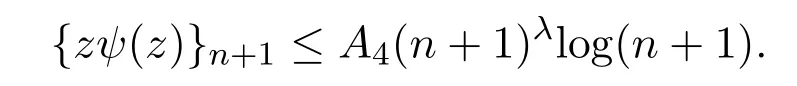
綜上可知,

其中

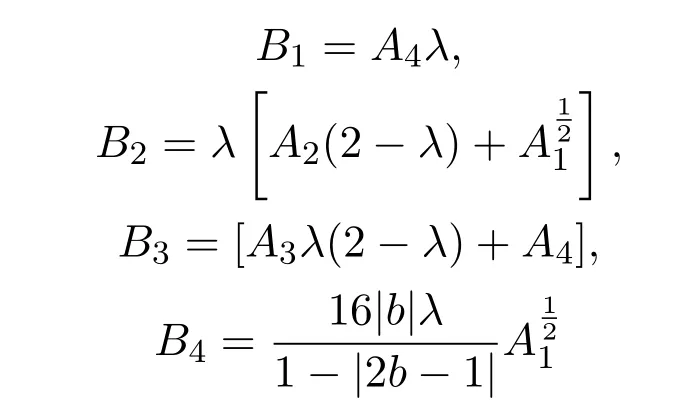
是絕對常數(shù).

[1]Duren P L.Univalent Functions[M].New York:Springer Verlag,1983.

[2]胡克.單葉函數(shù)的若干問題[M].武漢:武漢大學(xué)出版社,2001.

[3]鄧琴,葉中秋.單葉函數(shù)相鄰兩系數(shù)模之差的估計(jì)[J].江西師范大學(xué)學(xué)報(bào),2002,26(2):128-131.

[4]鄧琴.Bazilevic函數(shù)相鄰兩系數(shù)模之差的估計(jì)[J].數(shù)學(xué)學(xué)報(bào),2006,49(5):1195-1200.

[5]Leung Y.Successive coefficients of starlike functions[J].Bulletin of the London Mathematical Society,1978,10:193-196.

[6]胡克.論擬凸函數(shù)的相鄰系數(shù)[J].江西師范大學(xué)學(xué)報(bào),1986,4:1-6.

[7]Ye Zhongqiu.On the successive coefficients of close-to-convex functions[J].Journal of Mathematical Analysis and Applications,2003,283:689-695.

[8]寧菊紅,葉中秋.圓對稱函數(shù)的相鄰系數(shù)[J].數(shù)學(xué)研究,2005,38(3):286-291.

[9]Al-Amiri H S,Fernando T S.On close-to-convex functions of complex order[J].International Journal of Mathematics and Mathematical Sciences,1990,13(2):321-330.

[10]Caglar M.The logarithmic coefficient inequality for close-to-convex functions of complex order[J].Journal of Mathematical Inequalities,2015,9(3):951-959.