劉麗亞,谷 峰

(杭州師范大學應用數學研究所;數學系,浙江杭州 310036)

1　引言和預備知識

Branciari[1]首次引入了矩形度量空間的概念,并給出了此空間中的Banach壓縮映象定理.此后,很多學者在此空間中研究了其他不同壓縮條件下的不動點問題[2?11],同時也給出了Banach壓縮定理和Kannan型不動點定理在矩形b-度量空間中的一些應用.本文受到上述結論的啟發(fā),將在矩形b-度量空間中討論耦合重合點和公共耦合不動點的存在性和唯一性問題,得到了一類新的公共耦合不動點定理,在很大程度上推廣了相關文獻[12]的一些結果.

在介紹主要結果之前,先介紹一些基本概念和已知結果.

定義1.1[1]設X 是非空集,d:X×X→[0,+∞),且?x,y∈X,滿足

(Rb1)d(x,y)=0當且僅當x=y;

(Rb2)d(x,y)=d(y,x);

(Rb3)d(x,y)≤s[d(x,u)+d(u,v)+d(v,y)],其中u,v∈X{x,y},同時u/=v.則稱(X,d)為矩形b-度量空間,且s≥1為矩形b-度量空間(X,d)的系數.

注1.1[13]每個度量空間都是矩形b-度量空間,每個矩形度量空間也為矩形b-度量空間(這時s=1).反之不一定成立.

定義1.2[13]設{xn}是矩形b-度量空間(X,d)中的序列.{xn}稱為X 中的Cauchy列,如果

定義1.3[13]設{xn}是矩形b-度量空間(X,d)中的序列.{xn}稱為X 中的收斂列,如果

定義1.4[13]矩形b-度量空間(X,d)稱為完備的,如果X 中的每一Cauchy列都收斂于X中的某個點.

注1.2[13]矩形b-度量空間(X,d)中的數列的極限點不一定唯一,且收斂列不一定是Cauchy列.

定義1.5[14]稱(x,y)∈X×X是映象F:X×X→X的耦合不動點,如果F(x,y)=x,F(y,x)=y.

定義1.6[15]稱(gx,gy)∈X×X是映象對F:X×X→X和g:X→X的重合耦合點,如果F(x,y)=gx,F(y,x)=gy.這時,稱(x,y)∈X×X 是映象對F:X×X→X 和g:X→X的耦合重合點.

定義1.7[15]稱(x,y)∈X×X是映象對F:X×X→X和g:X→X的公共耦合不動點,如果F(x,y)=gx=x,F(y,x)=gy=y.

定義1.8[16]設X為一非空集.映象對F:X×X→X和g:X→X稱為ω-相容的,如果當F(x,y)=gx且F(y,x)=gy,總有gF(x,y)=F(gx,gy).

定義1.9[17]設X是一非空集,是定義在X中的一偏序關系,函數T:X×X→X,g:X→X.T稱為具有混合g-單調性質,如果T(x,y)關于x是g-單調不減的,關于y是g-單調不增的,即對任意的x,y∈X,有

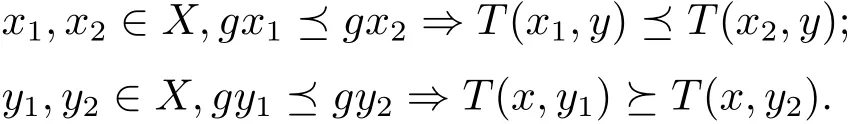
2　主要結果

為方便起見,下文中出現(xiàn)的函數ψ和φ均指滿足以下條件的函數[19]:

(1)ψ:[0,∞)→[0,∞)滿足:1)ψ是非減的且關于每個變元是連續(xù)的;2)ψ(t)=0當且僅當t=0.

(2)φ:[0,∞)→[0,∞)滿足:1)φ是下半連續(xù)的;2)φ(t)=0?t=0.

定理2.1設(X,d)是一個矩形b-度量空間,其系數s＞1,是定義在X上的一偏序.g:X→X為X上的自映象.映象T:X×X→X具有混合g-單調性.且滿足以下條件

(1)T(X×X)?g(X);

(2)?(x0,y0)∈X×X 使得gx0T(x0,y0),gy0T(y0,x0);

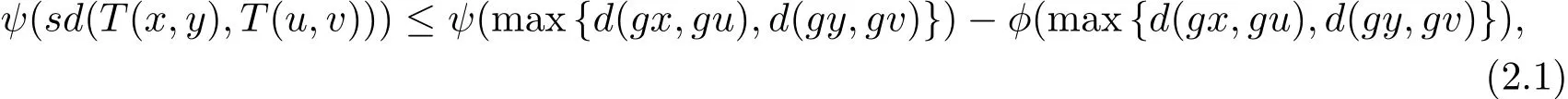
如果g(X)是(X,d)的完備子集,則g和T在X 中有重合耦合點.

證根據條件(2)可得,存在(x0,y0)∈X×X,使得gx0T(x0,y0),gy0T(y0,x0),由于T(X×X)?g(X),所以存在x1,y1∈X,使得gx1=T(x0,y0),gy1=T(y0,x0).類似的,存在x2,y2∈X,使得gx2=T(x1,y1),gy2=T(y1,x1).由于gx0T(x0,y0),gy0T(y0,x0),可得到gx0gx1,gy0gy1.由于映象T具有混合g-單調性,所以有依此類推,就可得到X 中的兩個序列{xn}和{yn},使得gxn=T(xn,yn),gyn=T(yn,xn),并且{gxn}和{gyn}還滿足

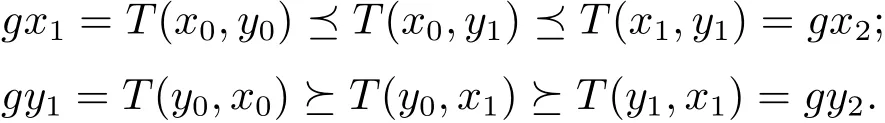
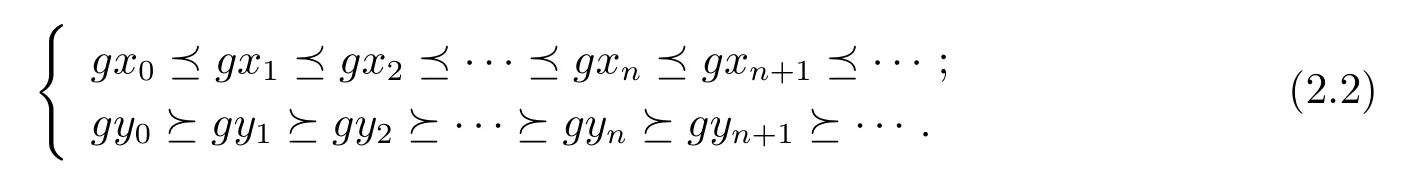
在式(2.1)中,取(x,y)=(xn,yn)和(u,v)=(xn+1,yn+1),并使用式(2.2)可得

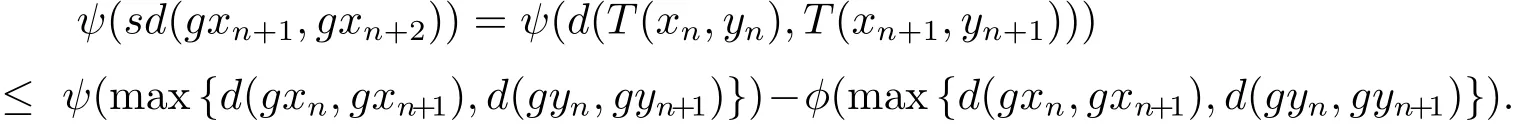
即

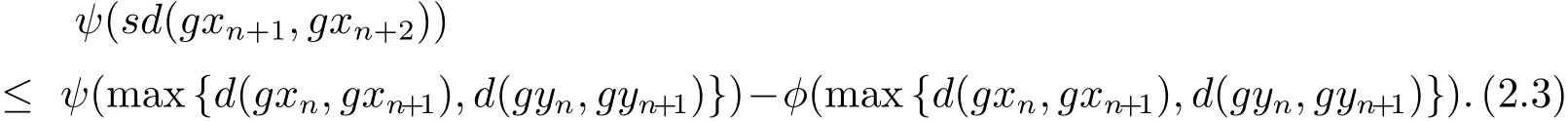
同理可得

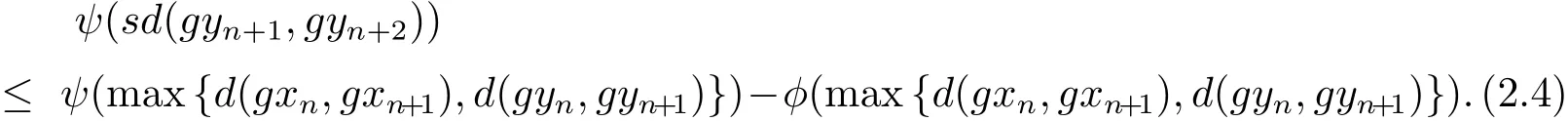
令

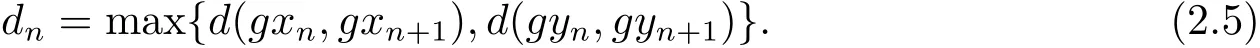
由于max{ψ(a),ψ(b)}= ψ(max{a,b}),?a,b∈ [0,+∞),進而有

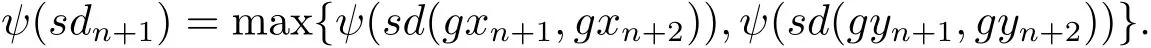
再根據(2.3),(2.4),(2.5)式和上式可得

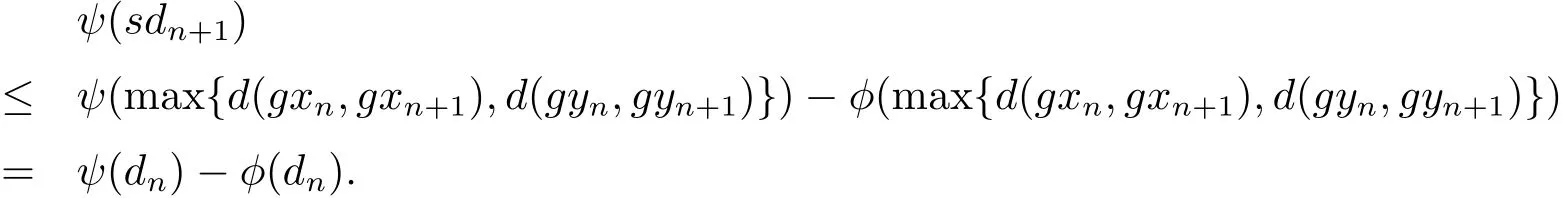
又由函數φ:[0,∞)→[0,∞),因此由上式可得

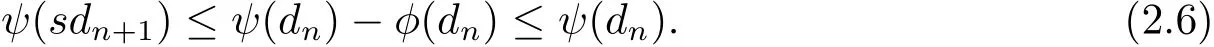
由ψ是非減的,可得

從而可知{dn}單調遞減的非負實數列,因此存在r∈[0,∞),使得式(2.6)兩邊令n→∞ 時,取極限得ψ(sr)≤ψ(r)?φ(r)≤ψ(r).由ψ是非減的,可得sr≤r.又由s＞1,所有當r＞0時,出現(xiàn)矛盾,進而可得r=0.于是有由式(2.5)可知

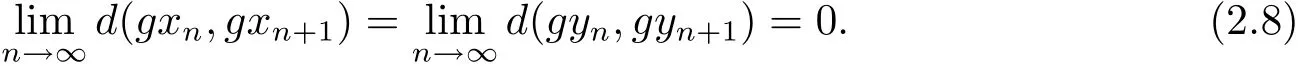
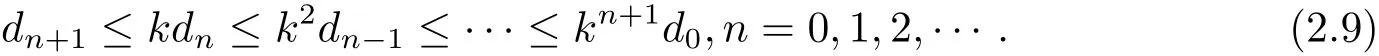
根據式(2.2),在式(2.1)中取(x,y)=(xn,yn)和(u,v)=(xn+2,yn+2),可得

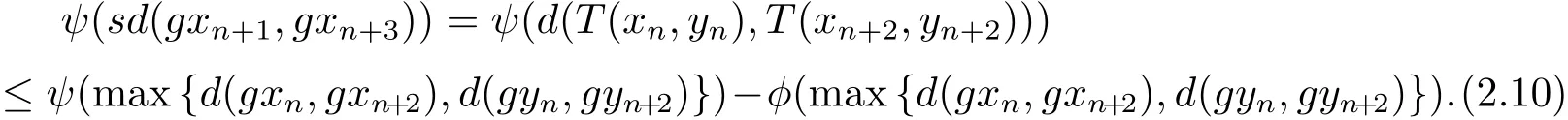
即

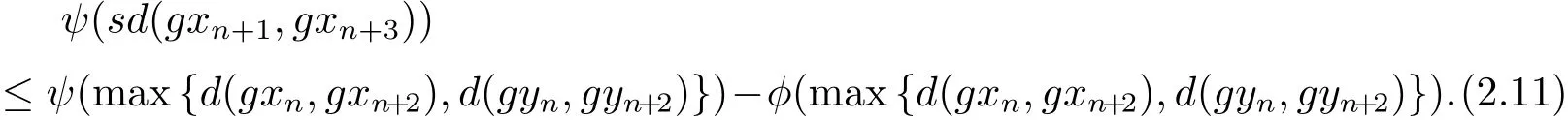
同理可得

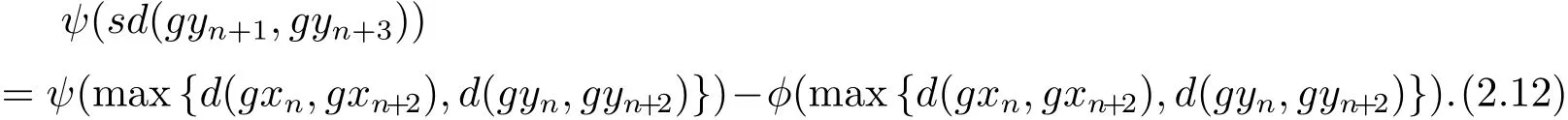
令

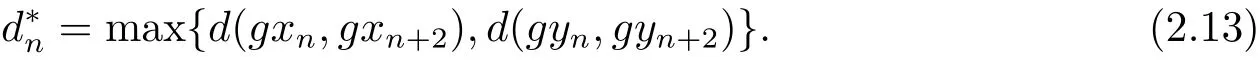
由于max{ψ(a),ψ(b)}= ψ(max{a,b}),?a,b∈ [0,+∞),進而有

再根據 (2.11),(2.12) 和 (2.13) 式可得又由 ψ 是非減的可知又由可知依次類推可得到

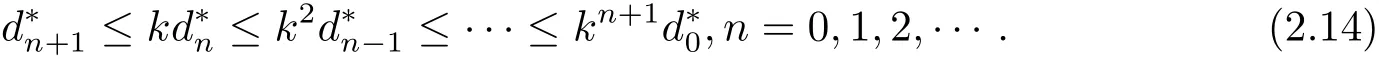
接下來,將證明{gxn}和{gyn}都是gX 中的Cauchy列.

a)當p是奇數時,設p=2m+1.

事實上,由性質(Rb3)可得

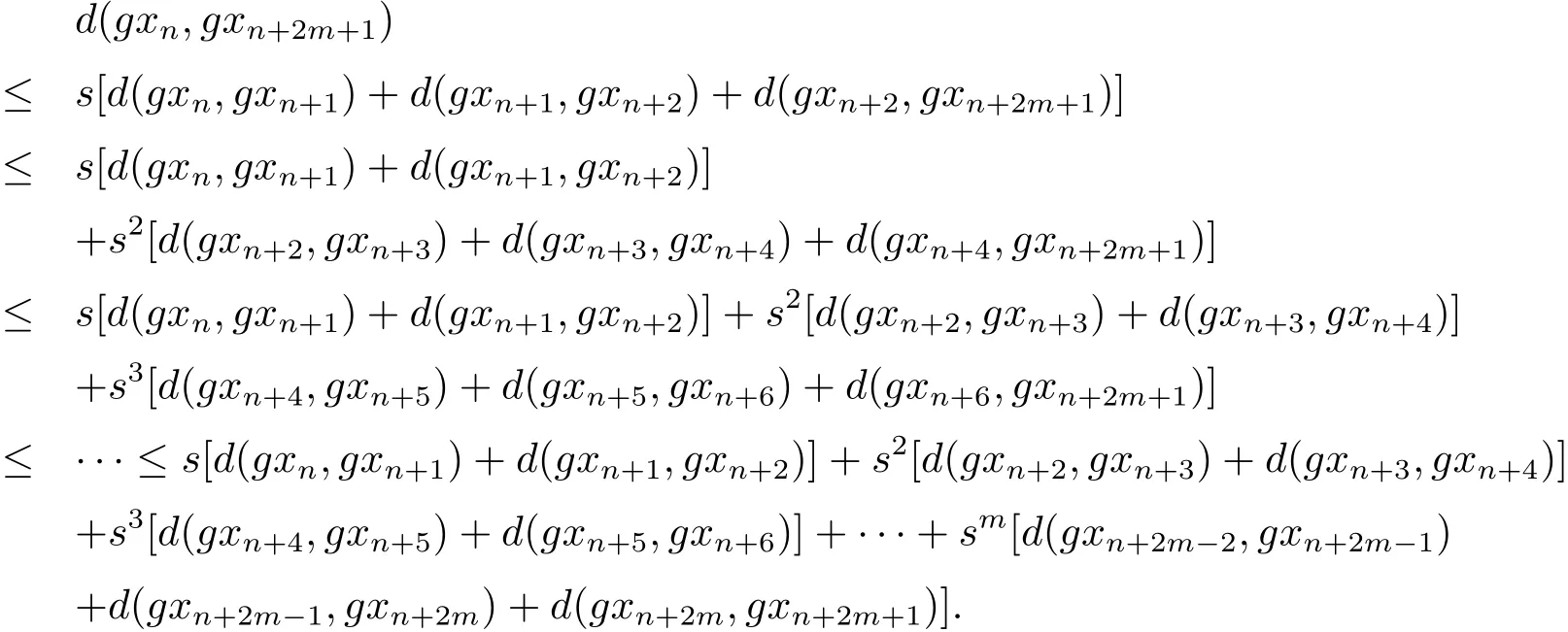
上式即

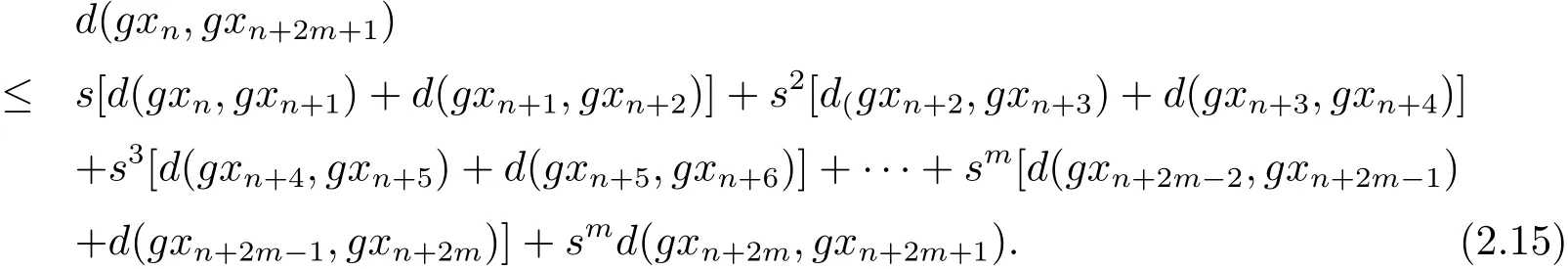
同樣道理可知

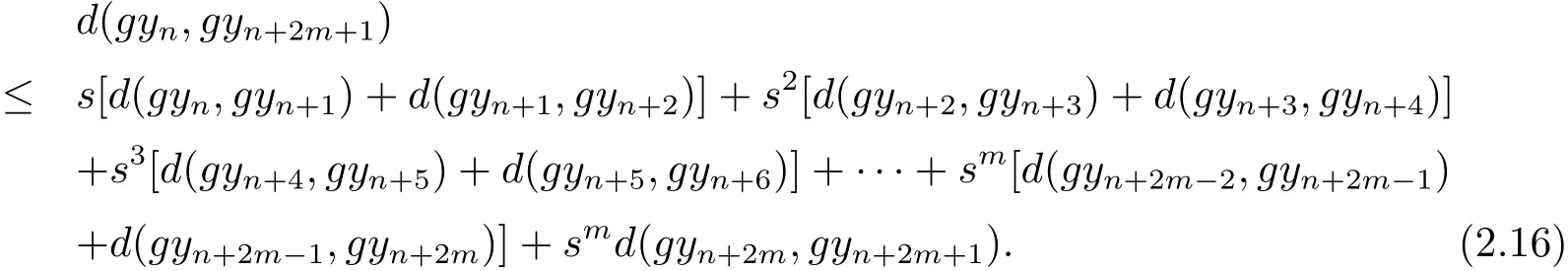
即

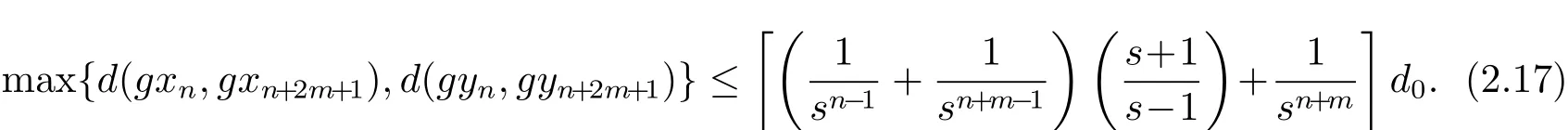
b)當p是偶數時,設p=2m.使用性質(Rb3)可得

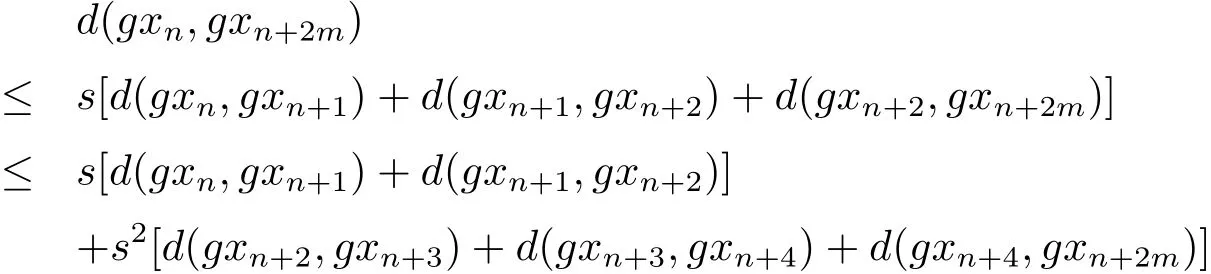
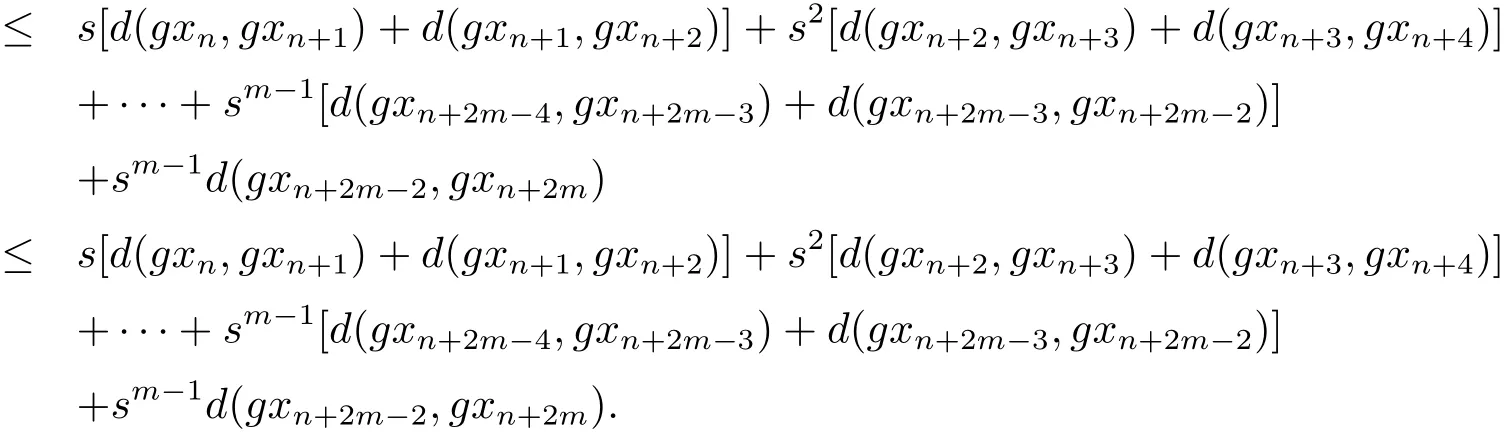
即

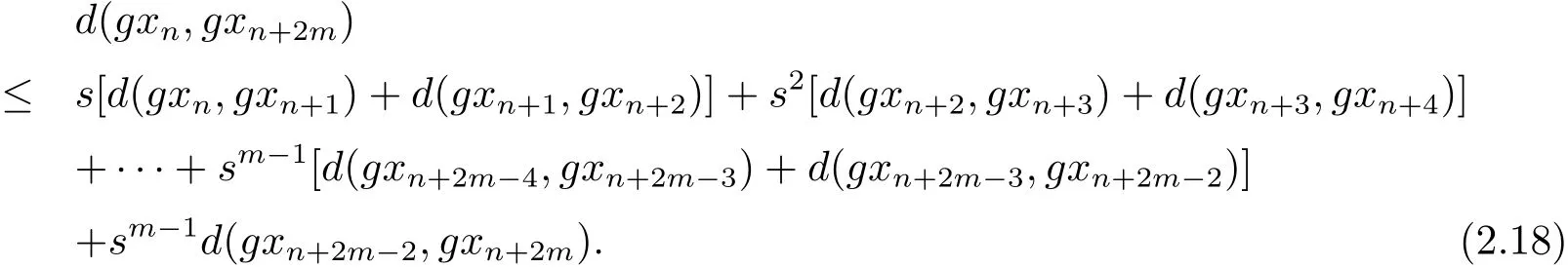
同樣道理可知

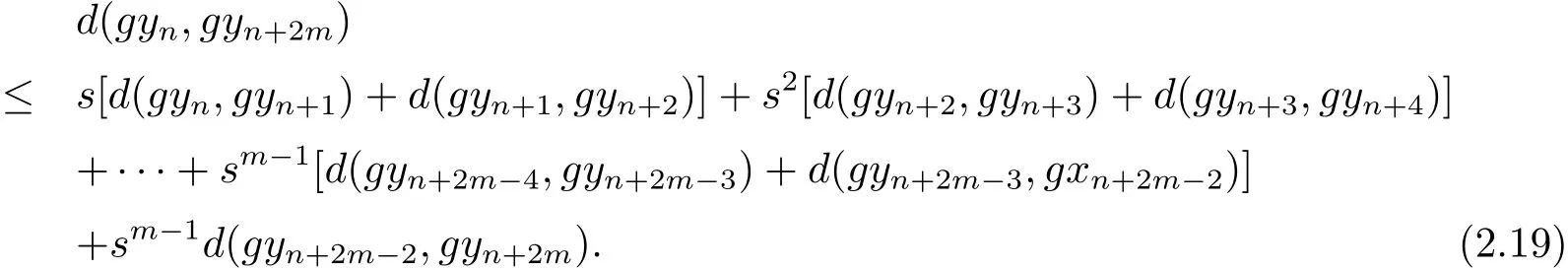
結合式(2.9),(2.14),(2.18)和(2.19)式,又由可得

進而可知

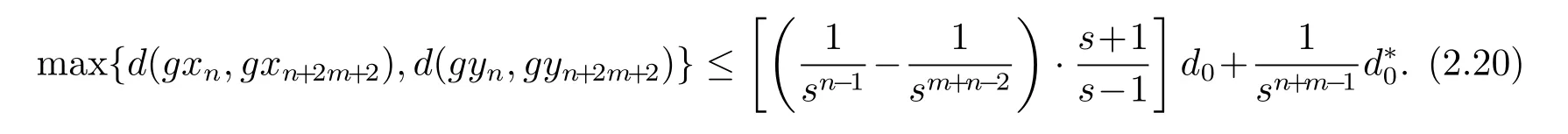
由(2.17)和(2.20)式可得

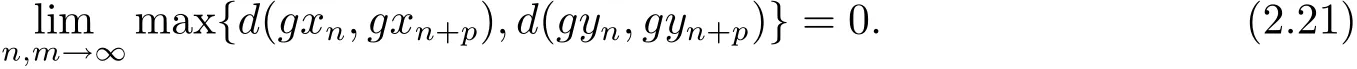
從(2.21)式可知{gxn}和{gyn}是g(X)中的Cauchy列.

又因為g(X)在是矩形b-度量空間(X,d)的完備子集,所以存在x,y∈X,使得

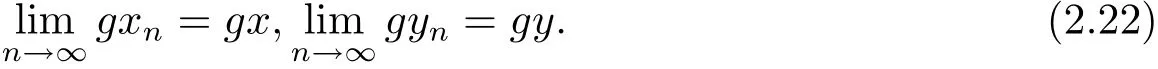
又由(2.1)式可得

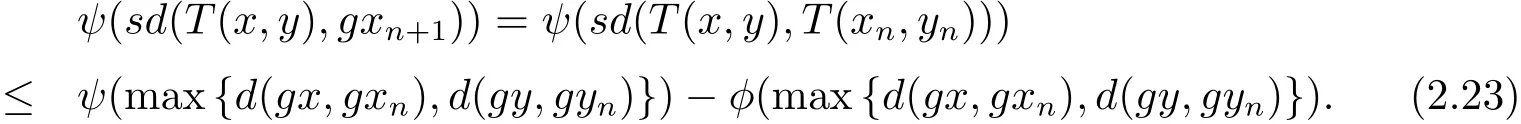
使用三角不等式

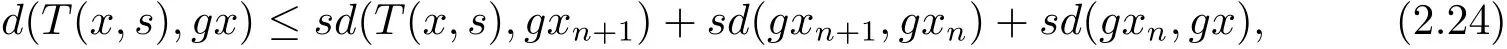
在(2.24)式中,令n→∞取極限,

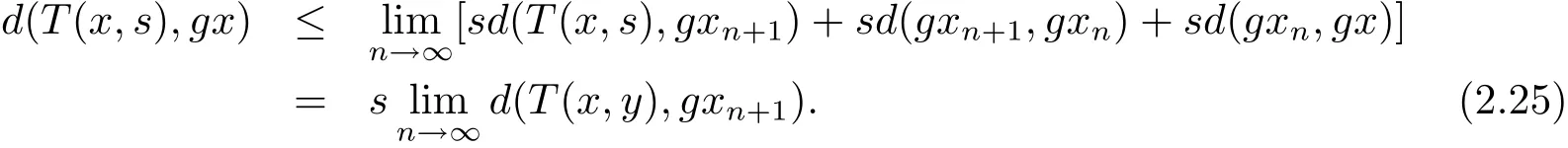
使用(2.22)和(2.25)式,在(2.23)式兩邊令n→∞取極限,可得

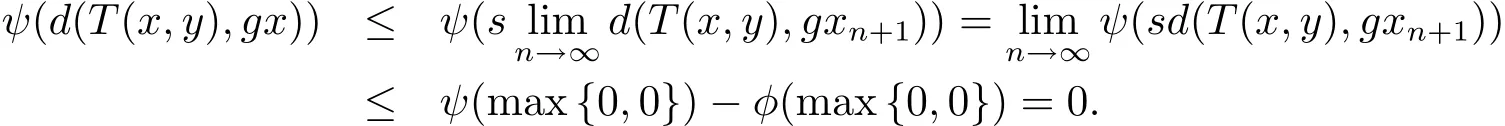
即d(T(x,y),gx)=0,進而可知T(x,y)=gx.同理可得T(y,x)=gy.從而有(gx,gy)是g和T的重合耦合點,證畢.

定理2.2設(X,d)是矩形b-度量空間,其系數s＞1,是定義在X 上的一個偏序.g:X→X為X上的自映象.映象T:X×X→X具有混合g-單調性.且滿足以下條件

(1)T(X×X)?g(X);

(2)?(x0,y0)∈X×X 使得gx0T(x0,y0),gy0T(y0,x0);

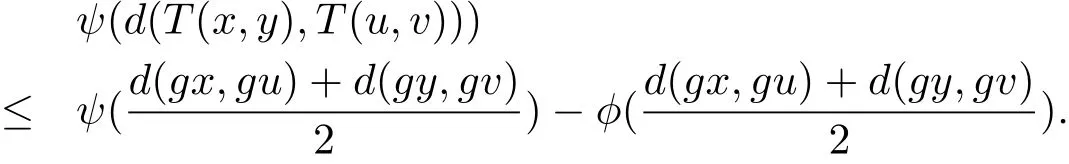
如果g(X)是(X,d)中的完備集,則g和T在X 中有重合耦合點.

證與定理2.1證明方法相同,略去.

注2.1令定理2.1中的自映象g為恒等映象I,即有下面推論.

推論2.1設(X,d)是矩形b-度量空間,其系數s＞1,是定義在X 上的一個偏序.映象T:X×X→X.如果滿足以下條件

(1)?(x0,y0)∈X×X 使得x0T(x0,y0),y0T(y0,x0);

則T在X中有耦合不動點.

注2.2?a,b,c∈[0,+∞),有

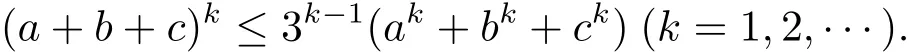
證顯然當k=1,2時結論成立,假設當k=m時結論成立,即

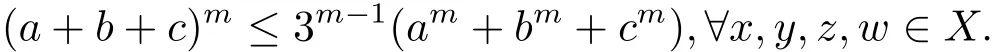
現(xiàn)證當k=m+1時結論也成立.事實上,有

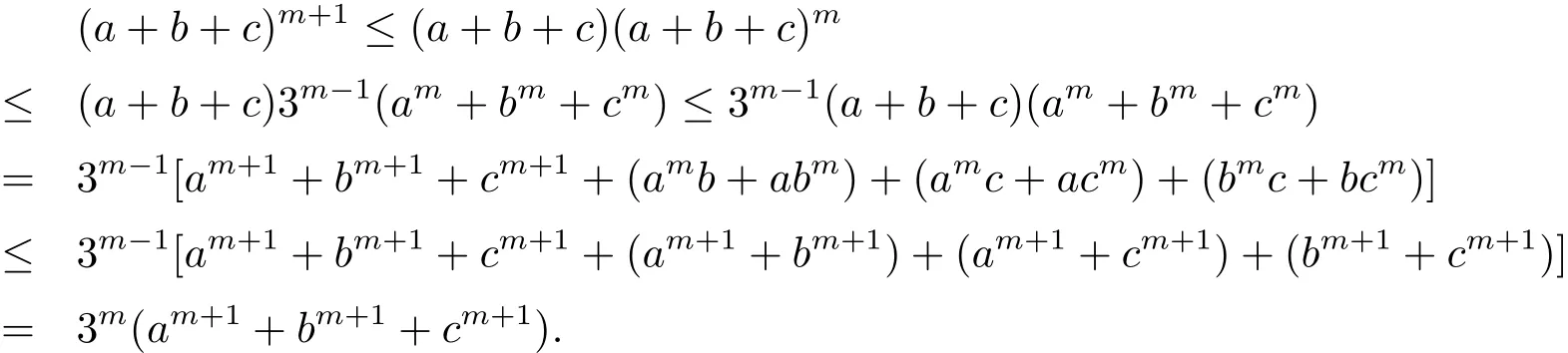
從而結論對一切自然數k成立.

例2.1設X=R,?x,y∈X,定義d(x,y)=(x?y)2,則(X,d)是一個系數s=3的矩形b-度量空間.設X上的偏序關系定義如下:xy?x≤y.定義函數T:X×X→R+和g:X→R+分別如下

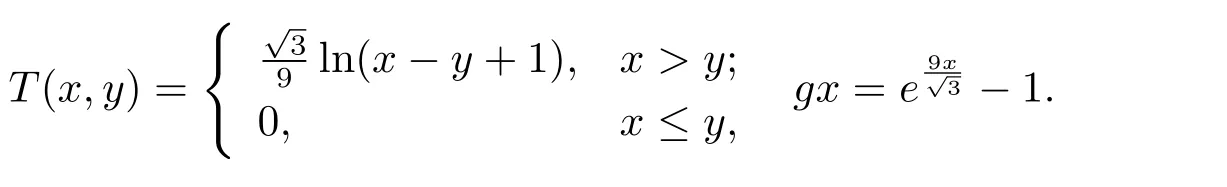
易得T(X×X)?g(X),且T具有g-混合單調性.當

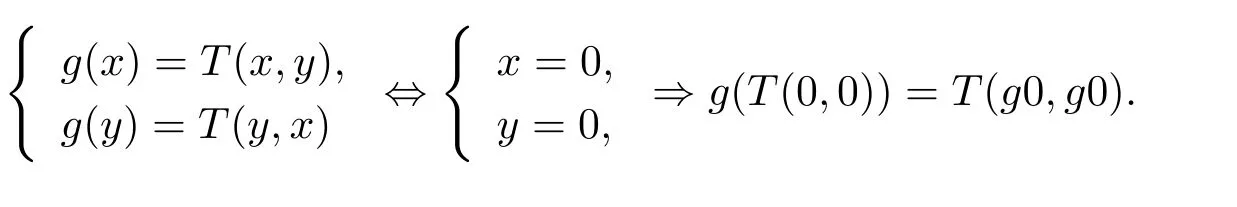
即F和g是ω-相容的.令(x,y)=(0,0)時,這時有g0T(0,0),g0T(0,0).

定義函數ψ,φ:R+→R+分別為

下面分四種情況討論.

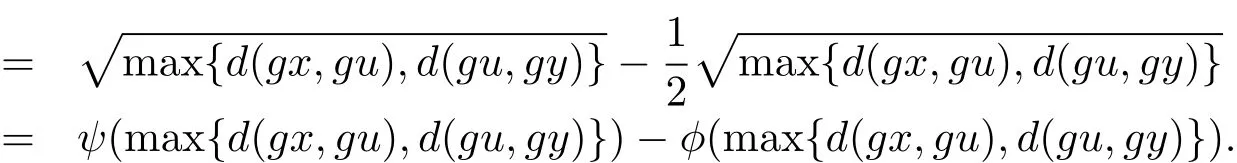
4)當T(x,y)=0,T(u,v)=0時,即x≤y,u≤v時,顯然成立.

從而根據定理2.1,可證得T和g具有耦合重合點,且T(0,0)=g0=0.

3　不動點的唯一性

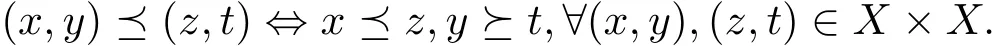
定理3.1在定理2.1的條件下,假設g和T是ω-相容的,且g和T的任意兩個重合耦合點(gx?,gy?)和(gz?,gt?)都有相應的公共可比較點(gu?,gv?)∈ X ×X,這時g和T 有唯一的耦合公共不動點.

證由定理2.1可知g和T至少存在一個重合耦合點.不妨假設(x,y),(z,t)∈X×X是g和T的任意兩個耦合重合點,即T(x,y)=gx,T(y,x)=gy和T(z,t)=gz,T(t,z)=gt.現(xiàn)證(gx,gy)=(gz,gt).

由已知條件可知,存在(u,v)∈X×X,使得(gu,gv)分別和(gx,gy),(gz,gt)都可比較.

a)當可比較關系為

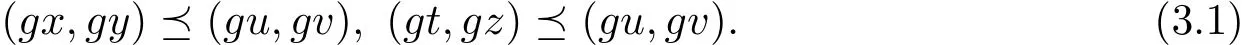
令

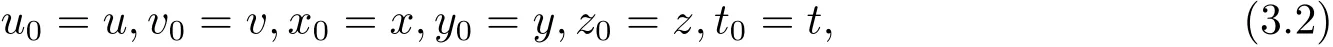
則?(u1,v1)∈X×X,使得

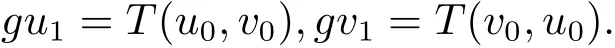
依次類推,會得到兩個數列{gun}和{gvn}分別為

同樣道理,可以得到數列{gxn},{gyn}和{gzn},{gtn}分別為

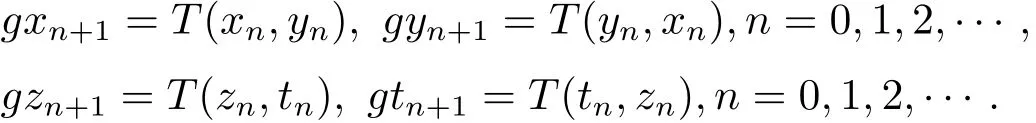
由于(x,y)是g,T的耦合重合點,則有

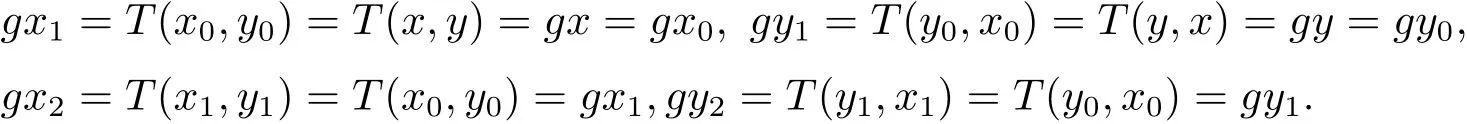
依次類推可知 gx0=gx1= ···=gxn= ···,gy0=gy1= ···=gyn= ···.即

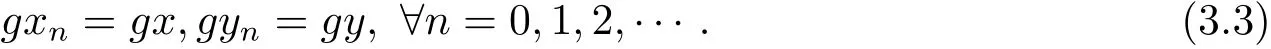
相同道理可知

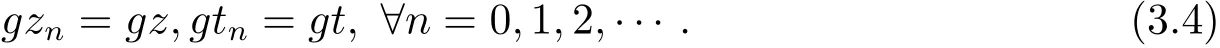
由于(3.1)和(3.2)式可得

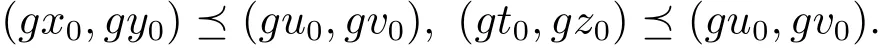
由于T具有混合g-單調性,所以可得

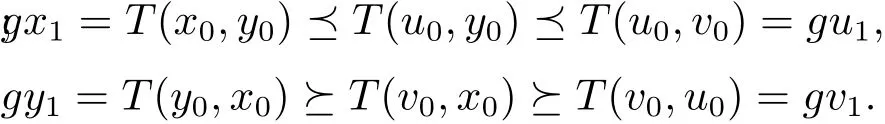
即(gx1,gy1)(gu1,gv1).同理可得(gx2,gy2)(gu2,gv2).這樣繼續(xù)做下去,可得

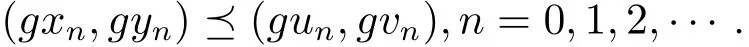
類似方法,可得

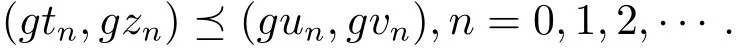
結合(3.3)和(3.4)式可得

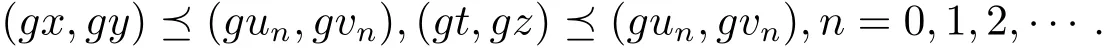
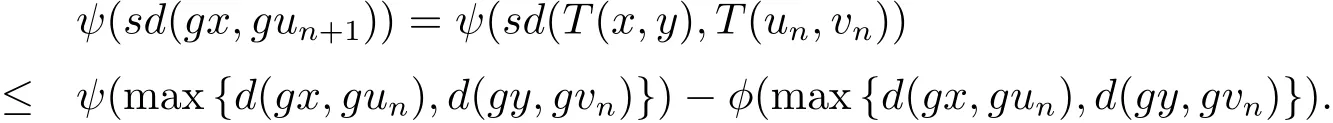
即

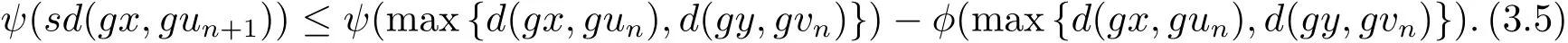
同理可得

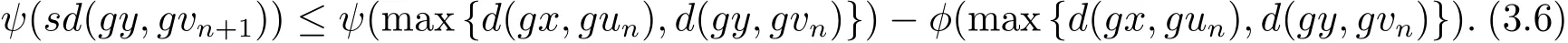
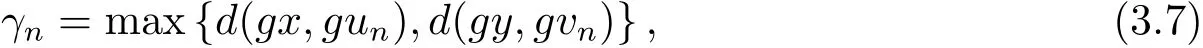
現(xiàn)令聯(lián)立(3.5),(3.6)和(3.7)式,又由max{ψ(a),ψ(b)}= ψ(max{a,b}),?a,b∈ [0,+∞),可得到

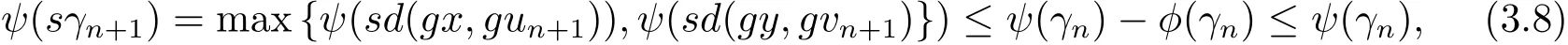
從而可得γn+1≤γn.所以可知{γn}單調遞減的非負實數列,存在r∈X,使得r≥0且因為將上式兩邊令 n → ∞ 時,取極限得ψ(sr)≤ψ(r)?φ(r).當r＞0時,出現(xiàn)矛盾.即r=0.于是有

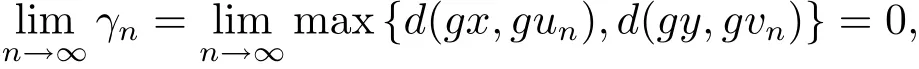
進而可知

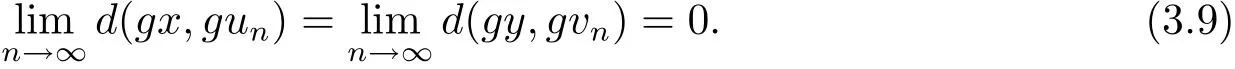
同樣道理可證得

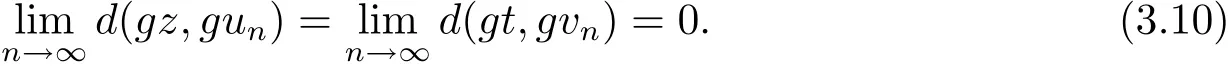
由(3.9)和(3.10)式可得到

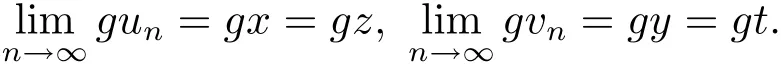
即(gx,gy)=(gz,gt).所以g和T具有唯一的重合耦合點.又因為g和T是ω-相容的,得到

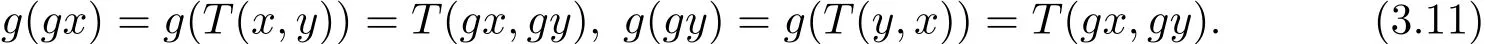
由于?m,n∈X,使得gx=m,gy=n,那么(3.12)式可整理為

因此(m,n)也是g和T的一個耦合重合點,由重合耦合點的唯一性知gm=gx=m,gn=gy=n.又由(3.12)式可得m=gm=T(m,n),n=gn=T(n,m).即證得g和T有耦合公共不動點.由于g和T的重合耦合點具有唯一性,因此g和T的耦合公共不動點也具有唯一性.

同a)的證明方法類似,上述三種情況同樣也能證得g和T的耦合公共不動點也具有唯一性.

4　在積分方程中的應用

假設X=C[a,b]是定義在[a,b]上的連續(xù)函數全體.≤是定義在X 上的偏序關系,定義

定義d:X×X→R+為

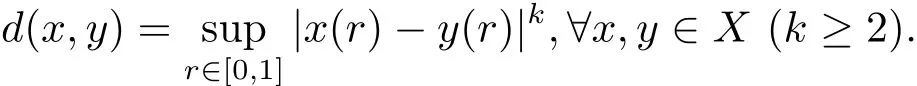
這時易知(X,d)是一個完備的矩形b-度量空間,由注2.2可知,其系數s=3k?1.

考慮以下積分方程組問題

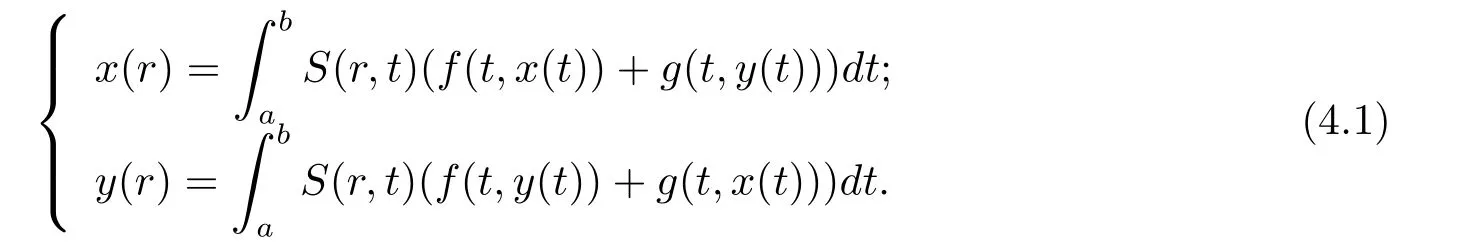
接下來,假設下面幾個條件成立.

(i)S(r,t):[a,b]×[a,b]→R+是連續(xù)函數.

(ii)f,g:[a,b]×R→R是連續(xù)函數.

(iii) ?(x0,y0)∈X×X,使得

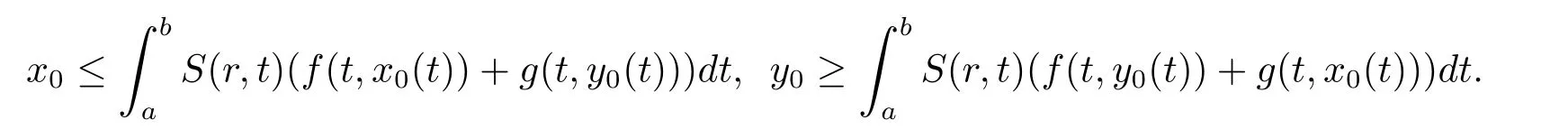
(iv)?μ,ν使得對于任意的r∈[a,b],x,y∈R,有

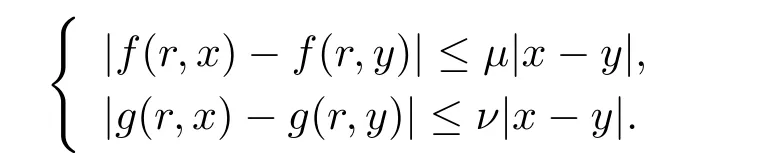
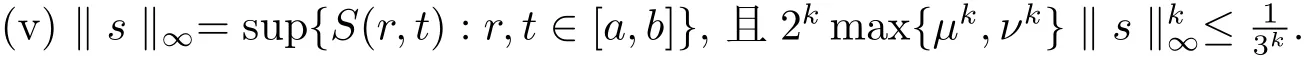
定理4.1由上述條件(i)–(v)成立,則積分方程組(4.1)有唯一的解.

證構造函數T:X×X→X和g:X→X如下

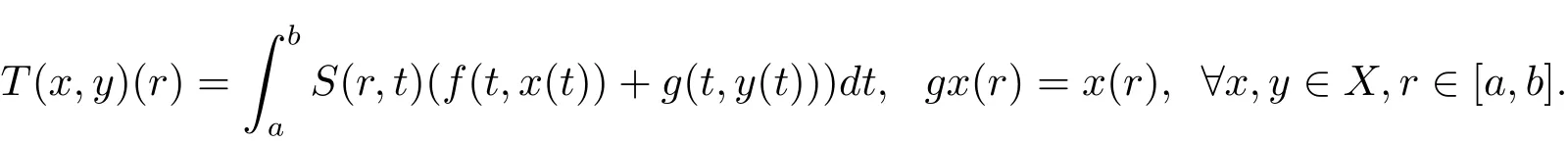
則由條件(iii)可知gx0T(x0,y0),gy0T(y0,x0),且g和T具有ω-相容性.又由條件(iv)和(v)可得

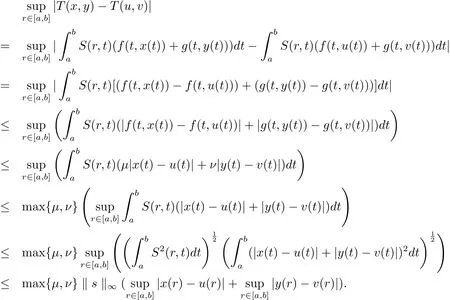
于是由條件(v),上式可整理為

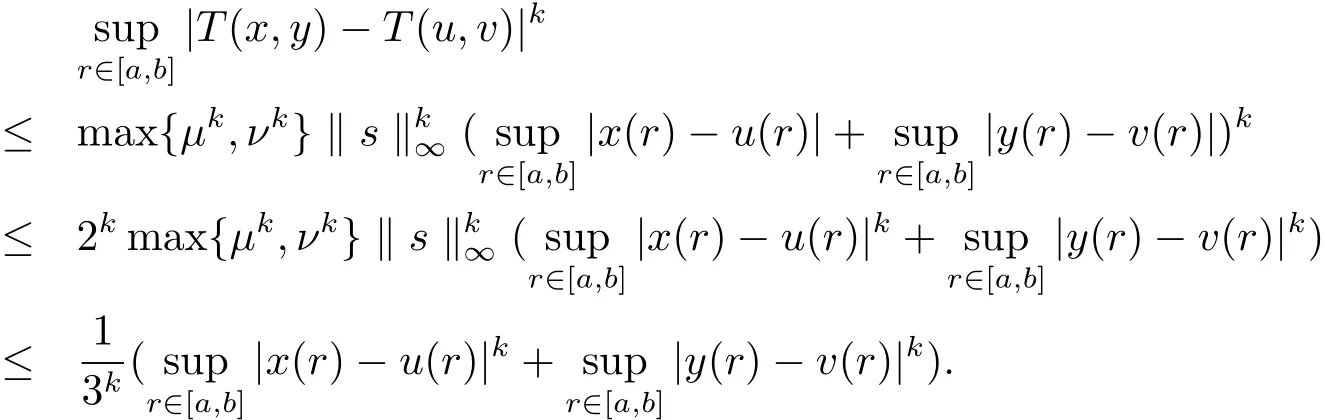
上式即為

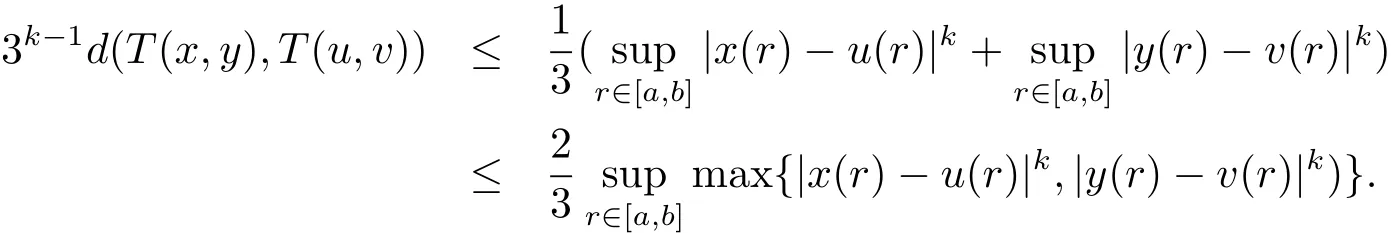
于是

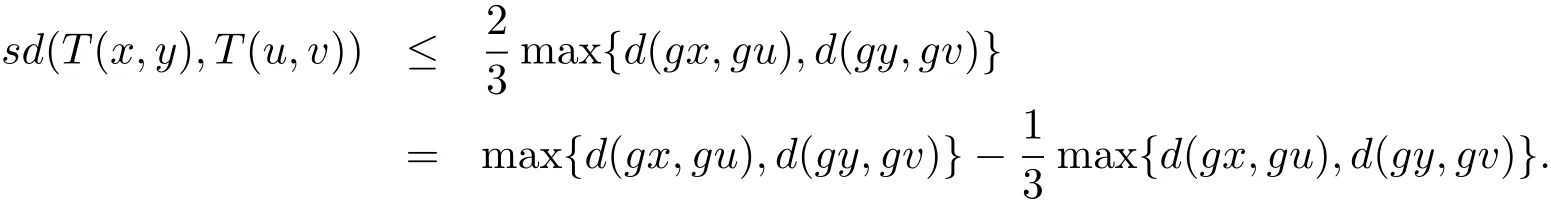
令函數ψ,φ:R+→R+分別為那么上式即為

ψ(sd(T(x,y),T(u,v)))≤ ψ(max{d(gx,gu),d(gy,gv)})?φ(max{d(gx,gu),d(gy,gv)}).由此易知定理3.1的所有條件被滿足,于是,存在(x?,y?)∈X×x,使得

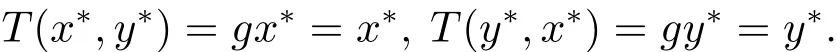
即(x?,y?)也為方程組(4.1)在C[a,b]上的唯一解.

[1]Bakhtin I A.The contraction mapping principle in quasimetric spaces[J].Funct.Anal.,Unianowsk Gos.Ped.Inst.,1989,30:26–37.

[2]Azam A,Arshad M.Kannan fixed point theorems on generalized metric spaces[J].J.Nonl.Sci.Appl.,2008,1:45–48.

[3]Azam A,Arshad M,Beg I.Banach contraction principle on cone rectangular metric spaces[J].Appl.Anal.Disc.Math.,2009,3:236–241.

[4]Chen C M.Common fixed point theorem in complete generalized metric spaces[J].J.Appl.Math.,Article ID 945915,2012.

[5]Das P.A fixed point theorem on a class of generalized metric spaces[J].Korean J.Math.Sci.,2002,9:29–33.

[6]Das P,Dey L K.A fixed point theorem in generalised metric spaces[J].Soochow J.Math.,2007,33(1):33–39.

[7]Lahiri B K.Das,P.Fixed point of a Ljubomir Ciric’s quasi-contraction mapping in a generalized metric space[J].Publ.Math.Debrecen,2002,61(3-4):589–594.

[8]Das P,Lahri B K.Fixed point of contractive mappings in a generalised metric space[J].Math.Slovaca,2009,59(4):499–504.

[9]Erhan I M,Karapinar E,Sekuli′c T.Fixed points of(ψ,φ)contractions on rectangular metric spaces[J].Fixed Point Theory Appl.,2012,138,DOI:10.1186/1687-1812-2012-138.

[10]Lakzian H,Samet B.Fixed points for(ψ,φ)-weakly contractions mapping in generalized metric spaces[J].Appl.Math.Lett.,2012,25(5):902–906.

[12]魏利,周海云.Banach空間中有限個增生算子公共零點的帶誤差項的迭代格式[J].數學雜志,2009,29(3):329–334.

[12]Gu F.Some new common coupled fixed point results in two generalized metric spaces[J].Fixed Point The.Appl.,2013,2013:181,DOI:10.1186/1687-1812-2013-181.

[13]Branciari A.A fixed point theorem of Banach-Caccippoli type on a class of generalized metric spaces[J].Publ.Math.Debrecen,2000,57:31–37.

[14]Bhaskar T G,Lakshmikantham V.Fixed point theorems in partially ordered metric spaces and applications[J].Nonl.Anal.,2006,65:1379–1393.

[15]Lakshmikantham V,′Ciri′c L B.Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces[J].Nonl.Anal.,2009,70:341–4349.

[16]Abbas M,Khan M A,Radenov′?c S.Common coupled fixed point theorem in cone metric space for ω-compatible mappings[J].Appl.Math.Comput.,2010,217:195–202.

[17]Berinde V,Borcut M.Tripled fixed point theorems for contractive type mappings in partially ordered metric spaces[J].Nonl.Anal.,2011,74(15):4889–4897.

[18]谷峰.不動點定理與非線性算子迭代序列的收斂性[M].哈爾濱:黑龍江科技出版社,2002.