Strength of lntramolecular Hydrogen Bonds
JIANG Xiaoyu, WU Wei, MO Yirong
1 College of Ecological Environment and Urban Construction, Fujian University of Technology, Fuzhou 350108, P. R. China.
2 The State Key Laboratory of Physical Chemistry of Solid Surfaces, iChEM, Fujian Provincial Key Laboratory of Theoretical and Computational Chemistry and College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, Fujian, P. R.China.
3 Department of Chemistry, Western Michigan University, Kalamazoo, Michigan 49008, USA.
1 lntroduction
As one of the most fundamental concepts in chemistry,biology and material science, hydrogen bond (H-bond) has been extensively studied experimentally and theoretically1-6. It ubiquitously exists among molecules (intermolecularly) or within a single molecule (intramolecularly). One kind of prominent examples for the intramolecular H-bond (IMHB) is nucleic acids where H-bonding interactions among base pairs dominate the three-dimensional structures and help determine the physiological or biochemical properties of DNA molecules.In the past two decades, a number of strong and unconventional hydrogen bonds, such as resonance-assisted hydrogen bonds(RAHBs)7-11, have been identified and recognized. The proposal of RAHB comes from the observation of the crystal structures of β-diketo enols by Gilli and coworkers, who interpreted the enhanced intramolecular (also intermolecular)H-bonding interaction evidenced by the shortened H-bond distance in terms of resonance7. In β-diketone enols, the intramolecular ···O=C―C=C―OH··· H-bond, where donor and acceptor are connected through π-conjugated double bonds,is enhanced by the resonance and results in the shortening of O···O distances (2.39-2.44 ?, 1 ? = 0.1 nm)11. This shortening of the hydrogen bonds is associated with a decrease (i.e.,red-shift) of O―H vibrational frequencies and abnormal downfield1H NMR chemical shifts8. In general, π-electron delocalization results in the effective mixing of resonance forms, and is responsible for very strong H-bonds with low energy-barrier height for the proton-transfer reaction. For the instance of the enol form of acetylacetone (AcAc), which is a prototypical enolone and has been well studied both experimentally and theoretically, the ground state can be treated as a mixture of tautomeric forms I (enol-keto) and II(keto-enol)7,12,13.

Scheme 1 Tautomeric forms of acetylacetone (AcAc).
However, as Sanz et al. argued, the seemingly enhanced IMHBs in unsaturated compounds may simply result from the constraints imposed by the σ-skeleton framework14,15. Alkorta et al. also computed magnetic properties as a probe for the RAHB phenomenon and found that neither the spin-spin coupling constants nor the proton chemical shifts provide any evidenceforthe existenceof RAHBs16,17. Energy decomposition analysis of a series of conjugated dimers linked by H-bonds showed that the enhanced interactions mostly originate from the classical dipole-dipole (i.e., electrostatic)attraction as resonance redistributes the electron density and increases the dipole moments in monomers, and the covalence of H-bonds changes very little if the resonance is quenched at the same nuclear arrangement18. But we note that intramolecular H-bonds differ from intermolecular H-bonds,irrespective of whether they are coupled with the -conjugated system or not. As such, we need figure out computational strategies of evaluating both the strength of resonance19and the strength of IMHB20-28. The former can be tackled with our block-localized wavefunction (BLW) method which is the simplest variant of ab initio valence bond (VB) theory29-32and can shut down the resonance to efficiently derive the geometry and energetics for an electron-localized state33-35. Thus, the remaining question is how to evaluate the strength of IMHBs.
While the strength of intermolecular H-bond in a complex can be easily evaluated through a supramolecular approach where the H-bond strength is the energy variation from free monomers to the complex, there are difficulties in the proper evaluation of the strength of IMHB. Various approximated approaches thus have been developed28,36-39. Gilli et al.suggested that the H-bond strengths can be reasonably predicted from acid-base molecular properties, or the pKaslide rule27. But the simplest and most popular one is to rotate the bridging X―H group around the vicinal C―X bond by 180ofrom its equilibrium position between the two heavy atoms, and the subsequent energy variation along the rotation is taken as the H-bond energy19,40-42. As a further improvement, Wang et al. rotated relevant dihedral angles to disable IMHBs but compensated the steric effect involved in the rotation process which is derived from a model system where the H-bond donor is substituted by a methylene group23,43. A complex conformational analysis adopted by Jablonski et al. is also based on the energy differences among the conformers resulting from the rotation of the donor and acceptor groups to predict the energy of the H-bond24. By the use of appropriate reference molecules, isodesmic reactions can be designed to derive the H-bond energy44. Deshmukh et al. proposed the molecular tailoring approach on the basis of the systematic fragmentation scheme26,45. Obviously, the use of model systems or the change of geometries in the above approaches inevitably introduces indefinite factors to the measure of IMHB strengths.Alternatively, Bader's quantum theory of atoms in molecules(QTAIM) approach46has been extensively applied to the study of H-bonds39,47,48. But evidences show that the estimate of H-bond strengths based on the QTAIM topological properties is imperfect49. The natural bond orbital (NBO) method has been broadly used for the study of H-bonds50,51. But due to the non-optimalnatureofNBOs,thechargetransfer(hyperconjugation) energy has been proved to be highly overestimated52-56.
To shed light into the nature of IMHB assisted by resonance,in this paper we lay out a novel strategy including two unique approaches, namely our BLW method33-35and Edmiston's truncated localized molecular orbital (TLMO) technique57, to study two exemplary systems of intramolecular homonuclear O―H···O H-bonds including acetylacetone (AcAc) and o-hydroxyacetophenone (oHAP), as shown in Fig.1. Whereas the BLW method can examine the impact of π resonance on the structures and energetics of molecules with intramolecular H-bonding interaction, the TLMO technique can probe the magnitude of covalence in IMHBs57,58.
2 Method
2.1 Block-localized wavefunction (BLW) method
Within the VB theory, a conjugated system is described by a number of resonance structures whose wavefunctions can be individually defined with Heitler-London-Slater-Pauling(HLSP) functions as

where MLis the normalization constant,A? is the antisymmetrizer and φ2i-1,2iis a bond function composed of non-orthogonal orbitals φ2i-1and φ2i(or a lone pair if φ2i-1= φ2i).

The overall many-electron wave function for an adiabatic state is a linear combination of several important VB functions and the resonance energy is the energy difference between the most stable resonance structure and the adiabatic state. Ab initio VB theory has been rejuvenated in the past two decades with a few practical programs notably the XMVB32,59,60. To simplify the computational costs involved in Eq.(1), we can represent bond orbitals with nonorthogonal doubly occupied fragment-localized orbitals (or group functions)61-66. Based on the conventional VB ideas, we proposed the BLW method where a BLW corresponds to a unique electron-localized diabatic state (usually the most stable resonance state). The fundamental assumption is that the total electrons and primitive basis functions (χμ) can be divided into k subgroups (blocks),and each MO is block-localized and expanded in only one block. Assuming that there are mibasis and nielectrons for block i, we can express block-localized MOs for this block as

Fig.1 Two molecules of IMHBs studied in this work.

Subsequently, the BLW for a closed-shell is defined using a Slater determinant as

Orbitals in the same subspace are subject to the orthogonality constraint, but orbitals belonging to different subspaces are nonorthogonal. Thus, the BLW method combines the advantages of both MO and VB theories. The BLW method is available at the DFT level with the geometry optimization and frequency computation capabilities34,67. We note that the electron density (ρBLW) corresponding to the BLW state is different from the density for the ground state (ρ) which can be obtained by standard MO or DFT calculations.
2.2 Truncated localized MOs (LMO) approach
A covalent bond (Eq.(2)) is characteristic of sharing a pair of electrons between two bonding atoms. In the case of the X―H··Y H-bond, Y (typically O or N) supplies its lone pair to the opposite positively charged hydrogen and a H-bond thus in many ways is comparable to a dative bond, albeit with much lower strength. Consequently, the covalence in the H-bond can be similarly measured by the electron transfer from the lone pair to the X―H antibond orbital. Within the MO theory, this kind of n → σXH*hyperconjugative interaction can be well illustrated with the perturbation of the lone pair orbital by the anti-bond orbital as

where both φ(n) and φ(σ*XH) are strictly localized orbitals and φ'is a delocalized orbital with a small tail from the X―H antibond orbital. To properly evaluate the magnitude of n →σ*XHinteraction, it is necessary to get optimal localized orbitals.The conventional localization of canonical MOs νia unitary transformation results in localized MOs which are not strictly localized on bonds or atoms and possess small tails which reflect both the orthogonalization and delocalization effects.The orthogonalization of MOs within the constraint of one Slater determinant does not change the energy, and only the delocalization tail measures the n → σ*XHinteraction. Edmiston proposed a simple solution to evaluate the n → σ*XHenergy by truncating the tails of LMOs to get the strictly LMOs57. The truncated LMOs (TLMOs) can be subsequently reorthogonalized and used to compute the molecular energy.Compared with the original energy before the LMO truncation,the molecular energy change from LMOs to TLMOs is the n →σ*XHelectron transfer (or delocalization) energy. In addition,TLMOs result in the third kind of electron density ρTLMO. We have examined the hyperconjugation energy in propene with the TLMO method, and found that the results are quite accurate compared with the BLW data58.
2.3 Computational details
Standard B3LYP density functional theory (DFT)calculations with the basis set of 6-311+G(d,p) were performed throughout the work as this level of theory has been assessed for IMHBs and shown comparable with MP2/6-311+G(d,p)results14,15.Geometries of acetylacetone (AcAc) and o-hydroxyacetophenone (oHAP) were optimized with the GAMESS software68. The optimal localized structure of AcAc where electron pairs are strictly localized on the CC or CO bond or O atom are obtained with the BLW method, which is implemented to the in-house version of GAMESS. For the BLW computation of oHAP, there are six electrons localized on the benzene ring. Vibrational frequencies are computed with a scaling factor of 0.967969. The comparison of the geometrical parameters and vibrational frequencies computed with the standard B3LYP and the BLW-DFT methods reveals the impact of the resonance on both the structures and energetics of molecules with resonance-assisted IMHBs.
The nature of IMHB, which is of -symmetry in AcAc and oHAP, is further investigated with the truncated LMOs. Tails of LMOs of either the carbonyl or hydroxyl functional groups from the other group are truncated to get the TLMOs. This truncation procedure follows the unitary transformation of delocalized MOs to LMOs. All three major localization criteria,including the Boys scheme70, the Edmiston-Ruedenberg (E-R)scheme71and the Pipek-Mezey (P-M) scheme72, will be adopted for comparison. In addition, the QTAIM method is employed to analyze the topological properties of the electron densities in both delocalized and π localized states. The consequence of the truncation of LMOs in terms of energy and electron density changes will also be probed.
3 Results and discussion
3.1 Resonance effect on geometry and energy
Using the BLW method, we usually derive the most stable resonance (Lewis) structure which can be served as a reference for the evaluation of resonance effect on geometry, energetic and other properties by comparing with the ground state which can be derived with conventional MO or DFT methods at the same theoretical level. In AcAc (1), there are six conjugated electrons and the conjugation effect can be monitored by the variations of the CC and CO bond lengths. Our major results related to the H-bonds are listed in Table 1. Similar to malonaldehyde49, the conjugation remarkably shortens the single bonds of C―C (from 1.551 to 1.445 by 0.106 ?) and C―O (from 1.440 to 1.326 by 0.114 ?) but modestly lengthens both the double bonds of C=C (from 1.322 to 1.370 by 0.048?) and C=O (from 1.204 to 1.245 by 0.041 ?). At the DFT optimal geometry, the strict localization of π electrons on double bonds and oxygen atoms increases the molecular energy by 63.0 kcal·mol-1(1 kcal = 4.1868 kJ) which is defined as the vertical resonance energy (VRE). This is higher than the value in malonaldehyde (51.2 kcal·mol-1). The discrepancy (11.8 kcal·mol-1) reflects the hyperconjugation energy of the two methyl groups in AcAc to the π space. The BLW optimization results in the optimal localized structure whose parameters are comparable to those in non-conjugated systems. For instance,the C―C bond stretches to 1.551 ?, comparable to the bond length in ethane, while the C=C bond shortens to 1.322 ?,identical to the bond length in ethylene. Similarly, the C―O single and C=O double bond lengths are 1.440 ? and 1.204 ?,respectively. These numbers can be justified by the values in methanol and formaldehyde. The energy difference between the optimal delocalized and localized structures corresponds to the adiabatic resonance energy (ARE), which is 48.8 kcal·mol-1for AcAc, again higher than the value in malonaldehyde (37.7 kcal·mol-1).

Table 1 Selected optimal bond distances (?), νOa-H stretching vibrational frequency (cm-1) and resonance energy (RE, kcal·mol-1) at the B3LYP/6-311+G(d,p) level.
The structural and energetic changes for oHAP are much like the case of AcAc, but the magnitudes are reduced slightly. For instances, the conjugation shortens the single bonds of C―C and C―O by 0.091 (from 1.564 to 1.473) and 0.102 ? (from 1.442 to 1.340) and lengthens the double bonds of C=C and C=O by 0.027 and 0.032 ?, respectively. Accordingly, both the VRE and ARE are 46.6 and 37.3 kcal·mol-1, respectively, and higherthanthecorrespondingvaluesin o-hydroxybenzaldehyde(41.8and32.9kcal·mol-1,respectively). The differences, which are 40% of the gaps between AcAc and malonaldehyde, again reflect the hyperconjugation energy of the methyl group in oHAP to the π space. We also note the resonance energies (VRE and ARE) in oHAP are even lower than those in AcAc or malonaldehyde,and apparently due to the π pair on the C1=C2bond which prefers to participate the resonance within the benzene ring and achieve the largest stability (aromaticity). This can be verified by the optimal C1=C2bond distance (1.395 ?) in the BLW optimal geometry, which is close to the bond distance in benzene much more than in ethylene.
Apart from the expected changes as discussed in above, the localization of π electrons obviously weakens the IMHB in both systems. Experimentally it has been suggested that the strength of a H-bond (X―H··Y) is associated with the H-bond distances including X···Y and H···Y73,74. For the present cases of AcAc and oHAP, the O―H bond shortens by 0.034 and 0.021 ?, while the Oa···Odnotably increases by 0.25 and 0.16 ?, respectively. These changes are in accord with the red-shifting of the stretching vibrational frequency of the O―H bond (by 633 and 338 cm-1, respectively). The comparison of the data for AcAc and oHAP in Table 1 also indicates that the IMHB in oHAP is somewhat weaker than the H-bond in AcAc,as suggested by the H-bond lengths and vibrational frequencies.All these results seemingly provide very strong proofs for the proposal of resonance-assisted H-bond and differ from the criticism by Yá?ez and coworkers that RAHBs result from the constraints imposed by the σ-skeleton framework14-17.
The impact of π conjugation can also be visualized by plotting the electron density difference map (EDD) between DFT and BLW densities at the DFT optimal geometries, as shown in Fig.2 where the orange/cyan surface represents an increase/decrease in electron density. In both cases, we observe the movement of the π electrons away from the hydroxyl oxygen to the carbonyl oxygen through the CC double bond.Significantly, there is electron density depletion from the hydrogen atom which can be verified by population analyses.Thus, π electron resonance does reduce the hydrogen population and makes the hydrogen carry more positive charge.
3.2 Strength of intramolecular RAHB
As there is no clear-cut definition for the energy of IMHBs,differentapproacheswithvariousassumptionsand approximations have been proposed. Notably, Woodford examined the H-bond energies in MA and its substituted derivatives with five different approaches, and found significant differences among these estimates. For instance, the IMHB energy in malonaldehyde ranges from 9.8 to 15.8 kcal·mol-139.

Fig.2 Electron density difference (EDD) isosurface maps showing the movement of electron density due to π conjugation in (a) AcAc and (b) oHAP.
We computed the most important index for the covalence of H-bonds, namely the electron transfer energy between the hydroxyl and carbonyl groups using the truncation approach.57For comparison, we also examined the energy change by flipping the ―OH group by 180°. Table 2 lists the results for AcAc and oHAP. It is notable that all three localization criteria result in very close values, though the Pipek-Mezey scheme based on the maximization of Mulliken populations gives slightly low numbers which will be used in the following discussion. Among the three localization schemes, the Pipek-Mezey scheme is the most effective one in differentiating σ and π MOs. This is important as the H-bond is of σ-symmetry and thus only σ-tails need be truncated, though the role of π tails should be negligible and in the present study both σ and π interactions are considered. For AcAc, the electron transfer,which is mainly the n → σ*XHhyperconjugative interaction but also composed of other trivial contributions, stabilizes the molecule by 14.6 kcal·mol-1, implying considerable covalent nature of the IMHB. For comparison, in the formic acid dimer which involves two intermolecular H-bonds, the optimal H-bond length R(O···O) is 2.701 ?, and the intermolecular interaction energy decomposition based on the BLW method(BLW-ED75,76) estimates the electron transfer stabilization energy for each H-bond as 5.3 kcal·mol-1, compared with the overall H-bond energy 8.3 kcal·mol-1if the deformation energy cost is not considered18.
However, the H-bond energy also concerns the repulsive Pauli exchange energy and the stabilizing electrostatic and polarization energies. This partly explains why the TLMO stabilization energies are lower than the energy variation by flipping the hydroxyl group out of the bonding area (11.0 kcal·mol-1for AcAc). The Pauli repulsion energy increases exponentially with the shortening of the H-bond length. The large electron transfer energy derived from TLMOs hardly offsets the fast increasing Pauli repulsion. Once the resonance is deactivated, we see the immediate lengthening of the H-bond(Table 1), and accordingly, there is a reduction of the electron transfer energy. There is an obvious correlation between the TLMO energy values and the H-bonding distances. However,we found that the H-bonding in oHAP is stronger than in AcAc if we estimate the H-bond strength by flipping the involved hydroxyl group, and this seems counterintuitive.
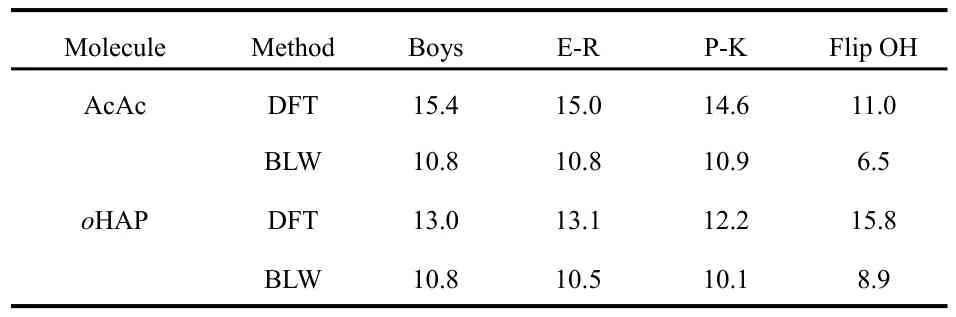
Table 2 H-bonding strengths (kcal?mol-1) estimated with the truncated LMO's based on various localization schemes.
Previous study with a series of resonance-assisted H-bonding systems including malonaldehyde showed that there is little change on the topological properties of electron densities at hydrogen bond critical points (HBCPs) when the resonance is shut down49. This raises a serious question whether QTAIM topological parameters can be a measure of H-bonding strength, though there are claims that the electron density at HBCPs is a good descriptor as it correlates well with hydrogen bond strengths77-79. Popelier et al. even suggested that the typical topological parameters at HBCPs are 0.002-0.04 a.u.for the electron density (ρ) and 0.02-0.15 au for its Laplacian(?2ρ).80,81Here we similarly compare the QTAIM topological parameters with the resonance turned on and off (Table 3). By retaining the same geometry, we again observe little changes between DFT and BLW densities. According to the concept of RAHB, the deactivation of the resonance would significantly weaken the H-bonding strength. Yet, we found that the topological parameters at HBCPs are dependent on the H-bond distance rather than the H-bond strength. In other words, the topological parameters will vary monotonously along with the H-bond distance, while the H-bonding strength would behave along a Morse curve like any interactions.

Table 3 The density and Laplacian of density at the BCP (in a.u.) with the DFT/6-311+G(d,p) geometries.
4 Conclusions
In this work, we employed the BLW method and the TLMO technique to study the impact of resonance on the structures and intramolecular hydrogen bonding in acetylacetone and o-hydroxyacetophenone which are exemplary for the concept of resonance-assisted hydrogen bond (RAHB). RAHB is characteristic of the cooperativity between the π-electron delocalization and H-bonding interactions. Computational results show that the π resonance significantly changes the molecular structures and shorten the IMHBs. Accordingly,remarkable red-shifting of the O―H stretching vibrational frequency is also verified, and the magnitude in acetylacetone is higher than in o-hydroxybenzaldehyde, suggesting the stronger bonding in the former. This is supported by the TLMO results, which show the significant covalence in IMHBs.
(1)Scheiner, S. Hydrogen Bonding: A Theoretical Perspectiνe; Oxford University Press: New York, 1997.
(2)Jeffrey, G. A. An Introduction to Hydrogen Bonding; Oxford University Press: New York, 1997.
(3)Desiraju, G. R.; Steiner, T. The Weak Hydrogen Bond In Structural Chemistry and Biology; Oxford University Press: New York, 2001.
(4)Hydrogen Bonding - Νew Insights; Grabowski, S. J., Ed.; Springer:Berlin, 2006; Vol.3.
(5)Gilli, G.; Gilli, P. The Νature of the Hydrogen Bond: Outline of a Comprehensiνe Hydrogen Bond Theory; Oxford University Press:New York, 2009; Vol.23.
(6)Supramolecular Assembly νia Hydrogen Bonds; Mingos, D. M. P.Ed.; Springer: Berlin, 2010; Vol.108.
(7)Gilli, G.; Bellucci, F.; Ferretti, V.; Bertolasi, V. J. Am. Chem. Soc.1989, 111, 1023. doi: 10.1021/ja00185a035
(8)Bertolasi, V.; Gilli, P.; Ferretti, V.; Gilli, G. J. Am. Chem. Soc. 1991,113, 4917. doi: 10.1021/ja00013a030
(9)Gilli, P.; Bertolasi, V.; Ferretti, V.; Gilli, G. J. Am. Chem. Soc. 2000,122, 10405. doi: 10.1021/ja000921+
(10)Gilli, P.; Bertolasi, V.; Pretto, L.; Ly?ka, A.; Gilli, G. J. Am.Chem. Soc. 2002, 124, 13554. doi: 10.1021/ja020589x
(11)Gilli, P.; Bertolasi, V.; Pretto, L.; Ferretti, V.; Gilli, G. J. Am.Chem. Soc. 2004, 126, 3845. doi: 10.1021/ja030213z
(12)Srinivasan, R.; Feenstra, J. S.; Park, S. T.; Xu, S.; Zewail, A.H. J. Am. Chem. Soc. 2004, 126, 2266.doi: 10.1021/ja031927c
(13)Sobczyk, L.; Grabowski, S. J.; Krygowski, T. M. Chem. Reν.2005, 105, 3513. doi: 10.1002/chin.200603277
(14)Sanz, P.; Mó, O.; Yá?ez, M.; Elguero, J. J. Phys. Chem. A 2007, 111, 3585. doi: 10.1021/jp067514q
(15)Sanz, P.; Mó, O.; Yá?ez, M.; Elguero, J. Chem. Εur. J. 2008,14, 4225. doi: 10.1002/chem.200701827
(16)Alkorta, I.; Elguero, J.; Mó, O.; Yá?ez, M.; Del Bene, J. E.Mol. Phys. 2004, 102, 2563.doi: 10.1080/00268970412331292885
(17)Alkorta, I.; Elguero, J.; Mó, O.; Yá?ez, M.; Del Bene, J. E.Chem. Phys. Lett. 2005, 411, 411.doi: 10.1016/j.cplett.2005.06.061
(18)Beck, J. F.; Mo, Y. J. Comput. Chem. 2007, 28, 455.doi: 10.1002/jcc.20523
(19)Grabowski, S. J. J. Phys. Org. Chem. 2003, 16, 797.doi: 10.1002/poc.675
(20)Grabowski, S. J. J. Mol. Struct. 2001, 562, 137.doi: 10.1016/S0022-2860(00)00863-2
(21)Grabowski, S. J. J. Phys. Chem. A 2001, 105, 10739.doi: 10.1021/jp011819h
(22)Grabowski, S. J. J. Phys. Org. Chem. 2004, 17, 18.doi: 10.1002/poc.685
(23)Wang, C. S.; Zhang, Y.; Gao, K.; Yang, Z. Z. J. Chem. Phys.2005, 123, 024307. doi: 10.1063/1.1979471
(24)Jablonski, M.; Kaczmarek, A.; Sadlej, A. J. J. Phys. Chem. A 2006, 110, 10890. doi: 10.1021/jp062759o
(25)Liu, T.; Li, H.; Huang, M. B.; Duan, Y.; Wang, Z. X. J. Phys.Chem. A 2008, 112, 5436. doi: 10.1021/jp712052e
(26)Deshmukh, M. M.; Gadre, S. R. J. Phys. Chem. A 2009, 113,7927. doi: 10.1021/jp9031207
(27)Gilli, P.; Pretto, L.; Bertolasi, V.; Gilli, G. Acc. Chem. Res.2009, 42, 33. doi: 10.1021/ar800001k
(28)Wendler, K.; Thar, J.; Zahn, S.; Kirchner, B. J. Phys. Chem.A 2010, 114, 9529. doi: 10.1021/jp103470e
(29)Valence Bond Theory; Cooper, D. L. Ed.; Elsevier:Amsterdam, 2002.
(30)Gallup, G. A. Valence Bond Methods: Theory and Applications; Cambridge University Press: New York, 2002.
(31)Shaik, S. S.; Hiberty, P. C. A Chemist's Guide to Valence Bond Theory; Wiley: Hoboken, New Jersey, 2008.
(32)Wu, W.; Su, P.; Shaik, S.; Hiberty, P. C. Chem. Reν. 2011,111, 7557. doi: 10.1021/cr100228r
(33)Mo, Y.; Peyerimhoff, S. D. J. Chem. Phys. 1998, 109, 1687.doi: 10.1063/1.476742
(34)Mo, Y.; Song, L.; Lin, Y. J. Phys. Chem. A 2007, 111, 8291.doi: 10.1021/jp0724065
(35)Mo, Y. In The Chemical Bond: Fundamental Aspects of Chemical Bonding; Frenking, G., Shaik, S., Eds.; Wiley-VCH:Weinheim, Germany, 2014, p. 199.doi: 10.1002/9783527664696.ch6
(36)Rozas, I. Phys. Chem. Chem. Phys. 2007, 9, 2782.doi: 10.1039/B618225A
(37)Estácio, S. G.; Cabral do Couto, P.; Costa Cabral, B. J.;Minas da Piedade, M. E.; Martinho Sim?es, J. A. J. Phys.Chem. A 2004, 108, 10834. doi: 10.1021/jp0473422
(38)Lipkowskia, P.; Kolla, A.; Karpfenb, A.; Wolschannb, P.Chem. Phys. Lett. 2002, 360, 256.doi: 10.1016/S0009-2614(02)00830-8
(39)Woodford, J. N. J. Phys. Chem. A 2007, 111, 8519.doi: 10.1021/jp073098d
(40)Latajka, Z.; Scheiner, S. J. Phys. Chem. 1994, 96, 9764.doi: 10.1021/j100203a035
(41)Scheiner, S.; Kar, T.; ?uma, M. J. Phys. Chem. A 1997, 101,5901. doi: 10.1021/jp9713874
(42)González, L.; Mó, O.; Yá?ez, M. J. Phys. Chem. A 1997, 101,9710. doi: 10.1021/ jp970735z
(43)Zhang, Y.; Wang, C. S. J. Comput. Chem. 2009, 30, 1251.doi: 10.1002/jcc.21141
(44)Rozas, I.; Alkorta, I.; Elguero, J. J. Phys. Chem. A 2001, 105,10462. doi: 10.1021/jp013125e
(45)Deshmukh, M. M.; Gadre, S. R.; Bartolotti, L. J. J. Phys.Chem. A 2006, 110, 12519. doi: 10.1021/jp065836o
(46)Bader, R. F. W. Atoms in Molecules: A Quantum Theory;Oxford University Press: Oxford, U. K., 1990.
(47)Pacios, L. F. J. Phys. Chem. A 2004, 108, 1177.doi: 10.1021/jp030978t
(48)LaPointe, S. M.; Farrag, S.; Bohrquez, H. J.; Boyd, R. J. J.Phys. Chem. B 2009, 113, 10957. doi: 10.1021/jp903635h
(50)Reed, A. E.; Curtiss, L. A.; Weinhold, F. Chem. Reν. 1988,88, 899. doi: 10.1021/cr00088a005
(51)Weinhold, F.; Landis, C. Valency and Bonding; Cambridge University Press: Cambridge, England, 2005.
(52)Pophristic, V.; Goodman, L. Νature 2001, 411, 565.doi: 10.1038/35079036
(53)Bickelhaupt, F. M.; Baerends, E. J. Angew. Chem. Int. Εd.2003, 42, 4183. doi: 10.1002/anie.200350947
(54)Weinhold, F. Angew. Chem. Int. Εd. 2003, 42, 4188.doi: 10.1002/anie.200351777
(55)Mo, Y.; Gao, J. Acc. Chem. Res. 2007, 40, 113.doi: 10.1021/ar068073w
(56)Mo, Y.; Wu, W.; Song, L.; Lin, M.; Zhang, Q.; Gao, J.Angew. Chem. Int. Εd. 2004, 43, 1986.doi: 10.1002/anie.200352931
(58)Mo, Y.; Zhang, Q. J. Mol. Struct. (Theochem) 1995, 357, 171.doi: 10.1016/0166-1280(95)04274-A
(59)Song, L.; Mo, Y.; Zhang, Q.; Wu, W. J. Comput. Chem. 2005,26, 514. doi: 10.1002/jcc.20187
(60)Song, L.; Chen, Z.; Ying, F.; Song, J.; Chen, X.; Su, P.; Mo,Y.; Zhang, Q.; Wu, W. XMVB 2.0: An ab initio Νon-orthogonal Valence Bond Program; Xiamen University:Xiamen, 2012.
(61)Mulliken, R. S.; Parr, R. G. J. Chem. Phys. 1951, 19, 1271.doi: 10.1063/1.1748011
(62)Sovers, O. J.; Kern, C. W.; Pitzer, R. M.; Karplus, M. J.Chem. Phys. 1968, 49, 2592. doi: 10.1063/1.1681576
(63)Stoll, H.; Preuss, H. Theor. Chim. Acta 1977, 46, 11.doi: 10.1007/BF02401407
(64)Kollmar, H. J. Am. Chem. Soc. 1979, 101, 4832.doi: 10.1021/ja00511a009
(65)Mehler, E. L. J. Chem. Phys. 1977, 67, 2728.doi: 10.1063/1.435187
(66)Gianinetti, E.; Raimondi; Tornaghi, E. Int. J. Quantum Chem.1996, 60, 157. doi: 10.1002/(SICI)1097-461X(1996)60:1<157:AID-QUA17>3.0.CO;2-C
(68)Schmidt, M. W.; Baldridge, K. K.; Boatz, J. A.; Elbert, S. T.;Gordon, M. S.; Jensen, J. J.; Koseki, S.; Matsunaga, N.;Nguyen, K. A.; Su, S.; Windus, T. L.; Dupuis, M.;Montgomery, J. A. J. Comput. Chem. 1993, 14, 1347.doi: 10.1002/jcc.540141112
(69)Andersson, M. P.; Uvdal, P. J. Phys. Chem. A 2005, 109,2937. doi: 10.1021/jp045733a
(70)Boys, S. F. Reν. Mod. Phys. 1960, 32, 296.doi: 10.1103/RevModPhys.32.296
(71)Edmiston, C.; Ruedenberg, K. Reν. Mod. Phys. 1963, 35, 457.doi: 10.1103/RevModPhys.35.457
(72)Pipek, J.; Mezey, P. G. J. Chem. Phys. 1989, 90, 4916.doi: 10.1063/1.456588
(74)Steiner, T.; Saenger, W. Acta Cryst. 1994, B50, 348.doi: 10.1107/S0108768193011966
(75)Mo, Y.; Gao, J.; Peyerimhoff, S. D. J. Chem. Phys. 2000, 112,5530. doi: 10.1063/1.481185
(76)Mo, Y.; Bao, P.; Gao, J. Phys. Chem. Chem. Phys. 2011, 13,6760. doi: 10.1039/c0cp02206c
(77)Mó, O.; Yánez, M.; Elguero, J. J. Chem. Phys. 1992, 97,6628. doi: 10.1063/1.463666
(78)Espinosa, E.; Molins, E.; Lecomte, C. Chem. Phys. Lett. 1998,285, 170. doi: 10.1016/S0009-2614(98)00036-0
(79)Espinosa, E.; Molins, E. J. Chem. Phys. 2000, 113, 5686.doi: 10.1063/1.1290612
(80)Koch, U.; Popelier, P. L. A. J. Phys. Chem. A 1995, 99, 9747.doi: 10.1021/j100024a016
(81)Popelier, P. L. A. J. Phys. Chem. A 1998, 102, 1873.doi: 10.1021/jp9805048
- 物理化學(xué)學(xué)報(bào)的其它文章
- 類單晶硅結(jié)構(gòu)Si(C≡C―C6H4―C≡C)4新材料的力學(xué)與光學(xué)性質(zhì):第一性原理研究
- Fukui Functions for the Temporary Anion Resonance States of Be-, Mg-,and Ca-
- Keggin型多酸負(fù)載的單原子催化劑(M1/POM, M = Ni, Pd, Pt, Cu,Ag, Au, POM = [PW12O40]3-)活化氮?dú)夥肿拥拿芏确汉碚撚?jì)算研究
- 嵌入配位不飽和金屬位對多孔芳香骨架材料儲氫性能的影響
- 符合獨(dú)立五元環(huán)規(guī)則的C100(417)Cl28形成機(jī)理的密度泛函理論研究
- 從能量和信息理論視角理解單取代烷烴的異構(gòu)化

