浙江溫州大學(xué)數(shù)信學(xué)院

徐彥輝 (郵編：325035)

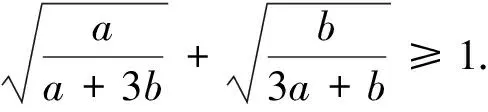
安振平先生在《不等式探究》一書中又提出如下兩個不等式,即[2]:

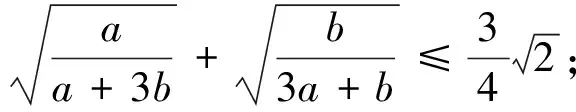
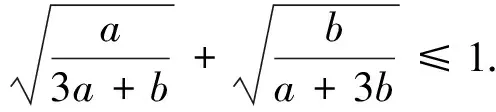
安振平先生通過兩邊平方化無理不等式為有理不等式,再分別運(yùn)用不同的方法和技巧證明了這兩個不等式.總之,這三個不等式的證明技巧性都比較強(qiáng),讀后雖然很受啟發(fā),但筆者觀察這三個不等式的特征,感覺到它們形式很相似,應(yīng)該有一種統(tǒng)一的方法可以證明這三個不等式,而且,還可以將這三個不等式推廣并給出證明.通過研究筆者確實找到了證明這三個不等式的統(tǒng)一方法,并給出了這三個不等式的推廣.為了使行文更簡潔,在此,先分別給出這三個不等式的推廣命題,然后再證明這三個推廣命題.

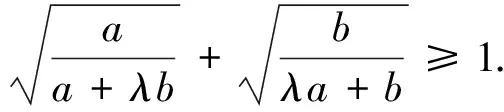
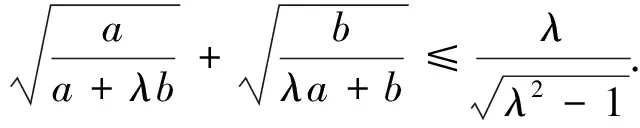
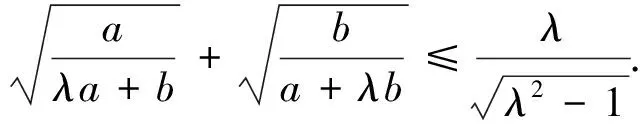
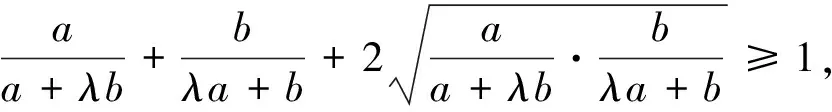
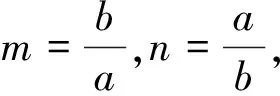
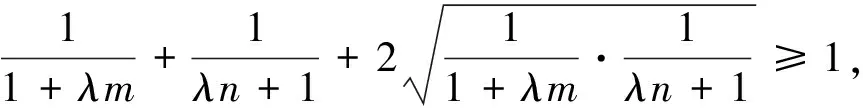
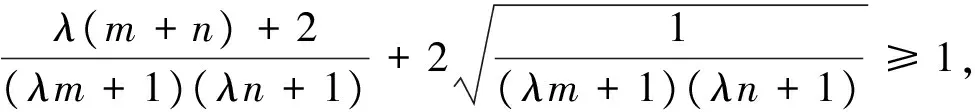
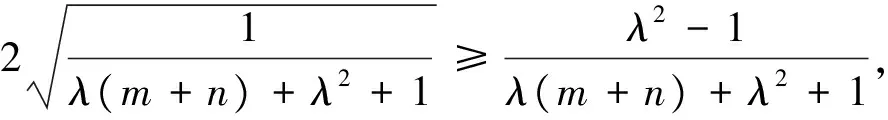
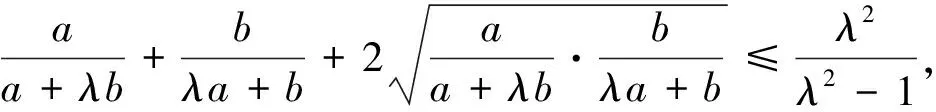
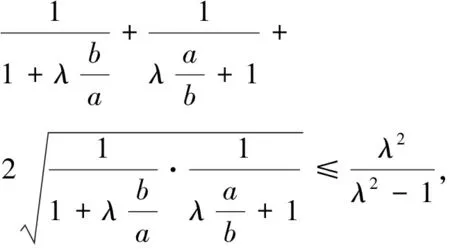
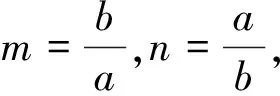
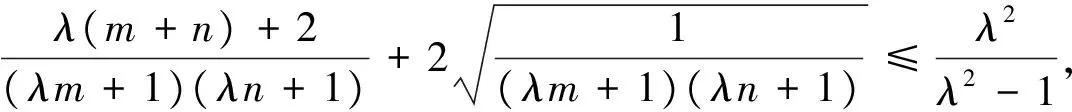
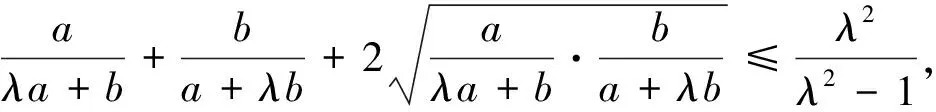
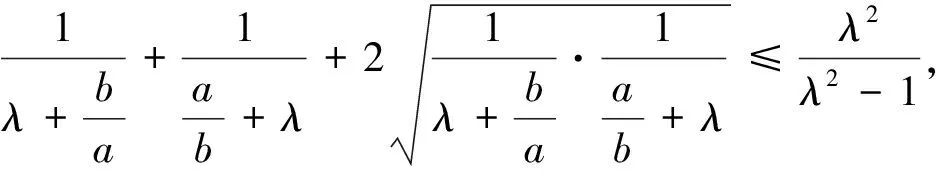
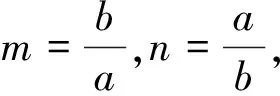
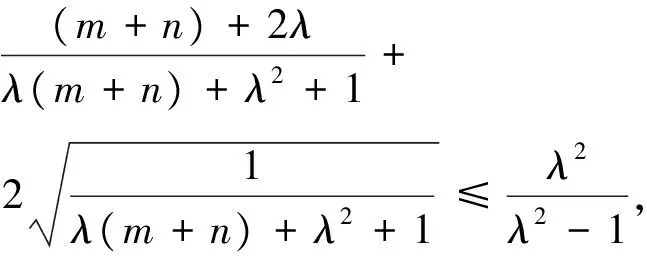
由m+n≥2，知

則只要證

由均值不等式知顯然成立,證畢.

1 安振平.數(shù)學(xué)問題與解答第1435號問題[J].數(shù)學(xué)通報,2003(5),封底

2 安振平.不等式探究[M].哈爾濱:哈爾濱工業(yè)大學(xué)出版社,2016