Feng-peng Bai,Zhong-hua Yang*,Wu-gang Zhou

State Key Laboratory of Water Resources and Hydropower Engineering Science,Wuhan University,Wuhan 430072,China

1.Introduction

Dam failures always cause enormous amounts of property damage and can be catastrophic for human life. Therefore, many researchers have made considerable efforts in past years to simulate and predict dam-break flows effectively. Mathematically, the dam-break problem is commonly described by shallow water equations. The accuracy, stability, and computational efficiency of numerical models are of crucial importance for numericalresults. However, the discontinuity in the dam site will cause spurious numerical oscillations and reduce the accuracy of the numerical model. Hence, it is key to use a proper numerical approach to handle with the flow near the discontinuity.

Either an artificial viscosity term in the equations or total variation diminishing(TVD)schemes are commonly used to suppress the spurious numerical oscillations near the discontinuity.The artificial viscosity term can improve the stability of numerical schemes.However,the viscosity coefficient is adjusted manually,which leads to arbitrary results.The TVD schemes are applied widely in gas dynamics and shallow waterflows.The main characteristic of TVD schemes is that they can reduce the spurious numerical oscillation across discontinuities,and additional artificial viscosity is not required.

The monotone upstream-centered scheme for conservation laws(MUSCL)approach,which has second-order accuracy in space,was put forward by van Leer(1979).Harten et al.(1983)and Sweby(1984)developed it into the TVD scheme using slope limiters.The MUSCL method is one of the most successful high-resolution schemes for hyperbolic conservation laws.Compared to other flow numerical models,the TVD MUSCL scheme is applied widely at present(Causon et al.,2000;Toro,2001;Liang et al.,2004;Liang,2011;Kim and Cho,2011).The TVD MUSCL-Hancock scheme has secondorder accuracy in both space and time.

In theory,the TVD scheme is only applicable to a single nonlinear conservation equation or constant coefficient equations in one-dimensional(1D)space.For nonlinear conservative equations,TVD schemes lack strict theoretical proof but have been verified to be effective through numerical experiments.Slope limiters can reduce the accuracy of numerical models,and different limiters cause an impact to different degrees.Most slope limiters have been developed by researchers in 1D space and extended to two-dimensional(2D)space or beyond by means of a dimension-splitting scheme(Toro,2001;Sanders and Bradford,2006).Slope limiters may also produce numerical dispersion in the process of extending them to 2D space or beyond,which affects the accuracy and stability of the mathematical model(van Albada et al.,1982;van Leer,1974).

This study developed a 2D shallow water model based on the TVD MUSCL-Hancock scheme and examined the effects of various limiters on the accuracy of the dam-break flow numerical model using a set of dam-break tests.The structured grid was selected due to its simplicity and ease of implementation.The slope limiter was used in the data reconstruction step,and the Riemann fluxes were calculated based on the reconstructed data.The source terms,including the friction and topography terms,may cause complex flows and make the comparative results of different slope limiters inconspicuous.This study focused on the effect of suppressing the spurious numerical oscillations near the discontinuity of different slope limiters,and the friction term and topographic factor were ignored.Reasonable suggestions are provided for selecting proper limiters in different cases.

2.Numerical model

2.1.Governing equations

The 2D non-linear shallow water equations can be derived by integrating the three-dimensional(3D)Reynolds-averaged Navier-Stokes equations over the depth.The conservativetype 2D shallow water equations,neglecting the viscous and friction terms,can be described as follows(Aliparast,2009;Erduran et al.,2002;García-Navarro and V′azquez-Cend′on,2000;Fraccarollo et al.,2003):

wheretdenotes time;xandyare Cartesian coordinates;U represents the conservative variables;F and G are the flux vectors in thexandydirections,respectively;and S is the source term vector.U,F,G,and S are expressed as

wherehis the water depth;uandvare the depth-averaged velocity components in thexandydirections,respectively;gis the gravitational acceleration;andzxandzyare the bed slopes in thexandydirections,respectively,withzx=-?z/?xandzy=- ?z/?y,wherezis the bed elevation.

2.2.TVD MUSCL-Hancock scheme

The variables are defined at the cell center in the TVD MUSCL-Hancock scheme,and the scheme achieves secondorder accuracy in space and time by(a)reconstructing the solution via piecewise linear functions,(b)evolving boundaryextrapolated values in time,and(c)solving a conventional(piecewise constant data)Riemann problem with initial data consisting of evolved boundary-extrapolated values.

The TVD MUSCL-Hancock scheme computes the cell interface flux in the following three steps.

2.2.1.Data reconstruction

The conservative variables at the left and right boundaries of the cell are obtained by the linear boundary extrapolation in thexdirection(Fig.1):

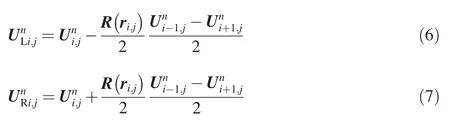
where superscriptndenotes the time level;subscripts L and R represent the left and right boundaries in a cell,respectively;subscriptsiandjare the cell indices;and R（ri,j）is the slope limiter,where ri,jis expressed as

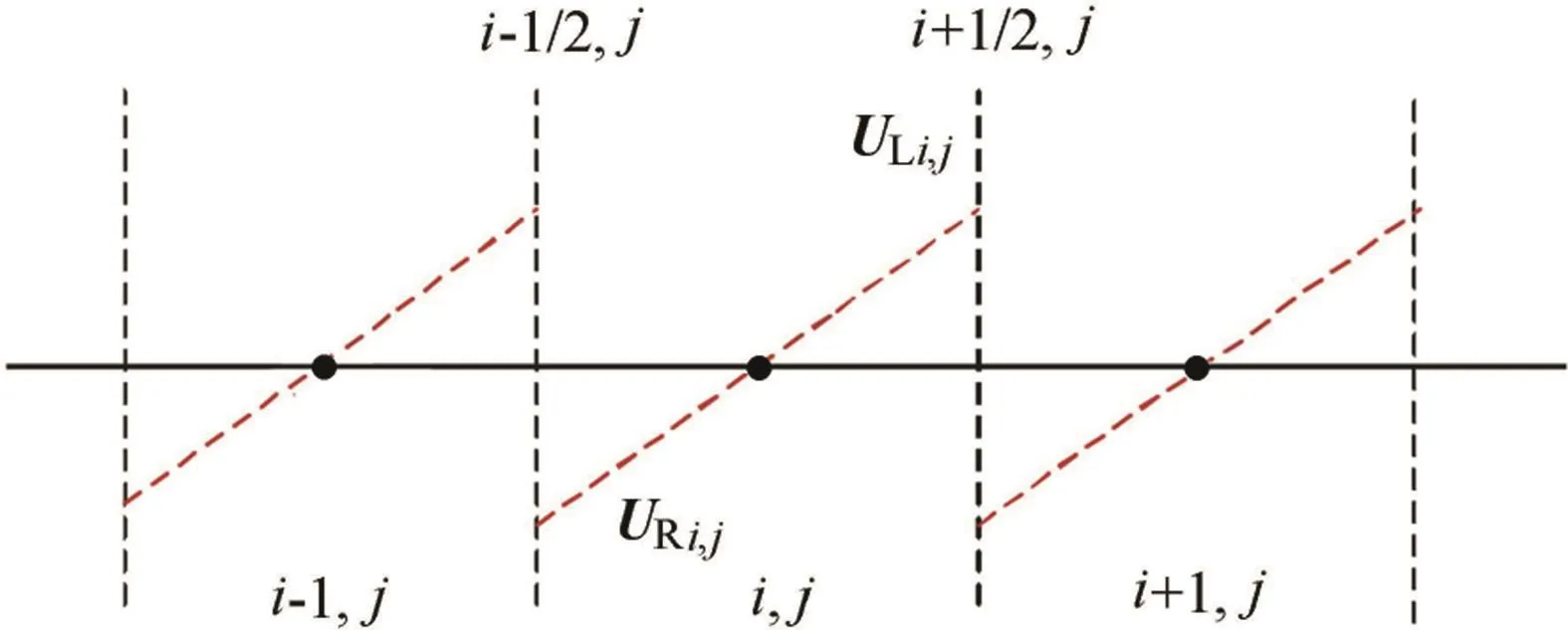
Fig.1.Data reconstruction.

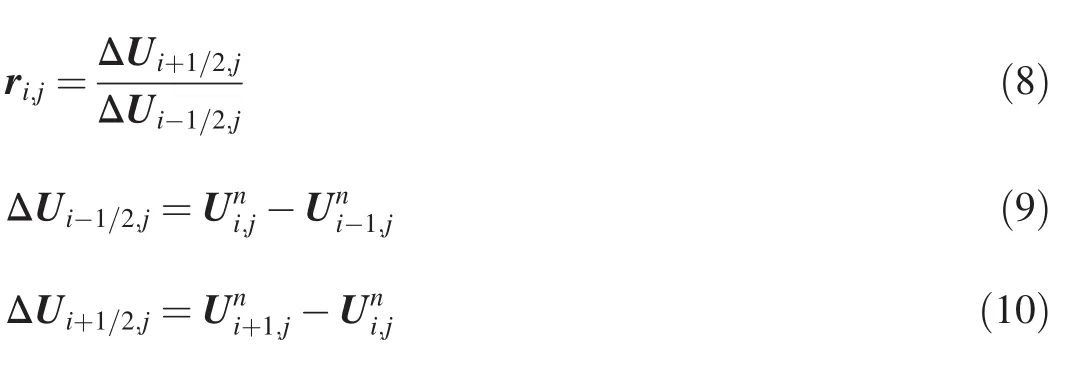
2.2.2.Evolution of extrapolated values

The boundary-extrapolated values in each cell are evolved by half the time step in terms of the corresponding conservative variables and according to the following for mulae:

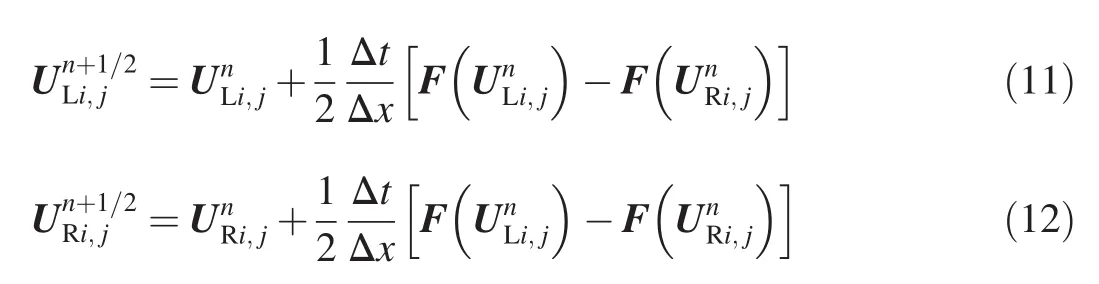
where Δxis the space step,Δtis the time step.Solutions can be obtained in theydirection in a similar way.

2.2.3.Riemann problem

Fluxes are computed at the cell interfaces based on the conservative variables obtained from the two steps above.The updating conservative formula is

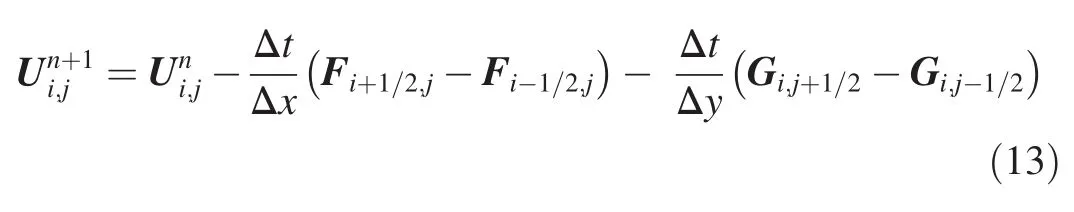
where Fi+1/2,jand Fi-1/2,jare the fluxes at the interfaces(i+1/2,j)and(i-1/2,j)in thexdirection,respectively,and Gi,j+1/2and Gi,j-1/2are the fluxes at the interface(i,j+1/2)and(i,j-1/2)in theydirection,respectively.

2.3.HLLC scheme

The Harten-Lax-van Leer-contact(HLLC)approximate Riemann solver(Fig.2),which is used to evaluate fluxes at the cell interfaces,is given in thexdirection(Toro,1999;Kim et al.,2008)as follows:

Fig.2.HLLC Riemann solver in x direction.

Wave speeds in the dry case at the left side of the structure(hL=0 andhR＞0)are as follows:

Wave speeds in the dry case at the right side of the structure(hR=0 andhL＞0)are as follows:

If the depthhin a grid is less than 10-6m,the grid is defined as being in a dry state.

Fig.3 shows the flow chart of the numerical model.

2.4.Slope limiters

The slope limiters play an important role in numerical shallow water models based on the finite volume method(Pu et al.,2012;Ata et al.,2013;Wu and Marsooli,2014).The TVD MUSCL-Hancock scheme uses slope limiters to suppress the spurious numerical oscillations near the dam site in the data reconstruction step.Most of the limiters are derived strictly for a single nonlinear conservation equation or constant coefficient equations in 1D space.For nonlinear conservative equations,slope limiters lack strict theoretical proof.The slope limiter in 1D space is defined asR(r)and must satisfy the TVD condition thatR（r）≤ min（4r/（1+r）,4/（1+r））forr≥ 0,which is labeled as the TVD limit in Fig.4.Whenr＜0,all limiters are equal to zero(van Albada et al.,1982).The following limiters are widely used whenr≥0:

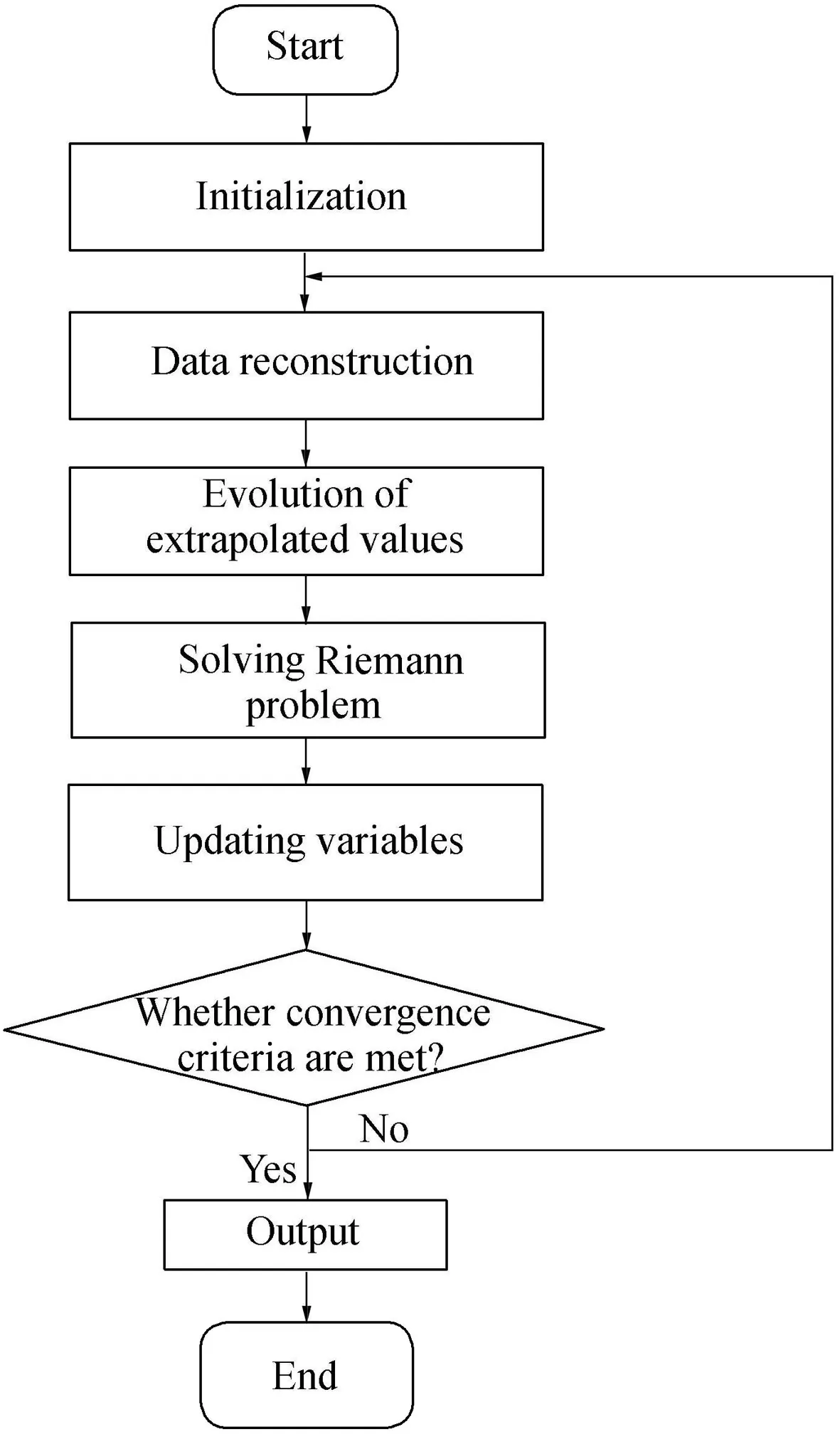
Fig.3.Flow chart of numerical model.

waves and increase the gradients ofu.As a result,these limiters,such as the super bee limiter,are antidissipative or compressive.

Fig.4 shows that all five limiters are dissipative to varying degrees.The minmod limiter is the most dissipative and the super bee limiter is more compressive than other limiters.For the double minmod limiter,a key feature is thatR(r)=1.0 for 1/3＜r＜3,showing that it yields the smallest truncation over the widest range ofr.

3.Numerical results and discussion

The friction term and topographic factor are ignored in all examples.The value of the gravitational acceleration is9.8m/s2.Both the upstream and downstream conditions are transmissive conditions.

3.1.1D dam-break examples

A horizontal and frictionless channel with a length of 50 m was considered,and a dam was located 20 m upstream of the channel.The thickness of the dam was neglected.The water depths upstream and downstream of the dam are denoted asHrandHt,respectively.

At the initial time,the upstream water depth was 10 m.The computational space step was 0.5 m,and the time step was 0.01 s.A comparative study of various limiters was conducted with different ratios ofHt/Hrby altering the downstream water depth and keeping the upstream water depth invariant.Fig.5 shows the results obtained att=0.8 s after instantaneous dam failure when the downstream water depth was 0.1 m(Ht/Hr=0.01).It is demonstrated that the minmod(Fig.5(a)),van Albada(Fig.5(d)),and van Leer(Fig.5(e))limiters are more dissipative,and the numerical model decreases to first-order accuracy near the discontinuity(x=30.5 m)and inflection points(x=14.0 m).The superbee(Fig.5(c))and double minmod(Fig.5(b))limiters simulate the water flow accurately near the discontinuity and keep second-order accuracy of the numerical model at the inflection points.Fig.6 shows comparative results between the exact solution and numerical solutions obtained from the five limiters near the first inflection point.It can be seen that the results of double minmod and superbee limiters agree better with the exact solution than those of other three limiters.

Fig.4.Diagram of slope limiters R(r).

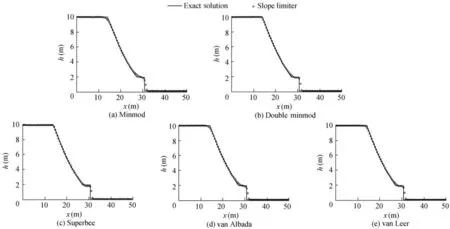
Fig.5.Comparison between exact solution and numerical solutions obtained from various limiters at t=0.8 with Ht/Hr=0.01.

Fig.7 shows the comparative results obtained att=0.8 s after instantaneous dam failure when the downstream water depth is 0.01 m(Ht/Hr=0.001).Owing to significant numerical dissipation,the minmod(Fig.7(a)),van Albada(Fig.7(d)),and van Leer(Fig.7(e))limiters fail to simulate the water flow near the discontinuity(x=33.6 m).The results of the parameter(h-1-h+1)/h0with various limiters are presented in Table 1,where(h-1-h+1)/h0denotes the relative error value of the water depth neighboring the discontinuity,h-1represents the numerical solution of water depth at the first grid node on the left of the discontinuity,h+1represents the numerical solution of water depth at the first grid node on the right of the discontinuity,andh0is the theoretical solution of water depth at the discontinuity.ForHt/Hr=0.2,the relative error(h-1-h+1)/h0of various limiters has no significant difference.However,for smaller ratios,such asHt/Hr= 0.01 orHt/Hr= 0.001,the nonphysical distortion of the minmod,van Albada,and van Leer limiters is more severe than that of the superbee and double minmod limiters.Based on the results of numerical experiments with many ratios ofHt/Hr,the minmod,van Albada,and van Leer limiters are not used to simulate the dam-break problems when the ratio of the downstream water depth to the upstream water depth is less than 0.01.The superbee limiter or double minmod limiter is a better choice for the smaller ratios.

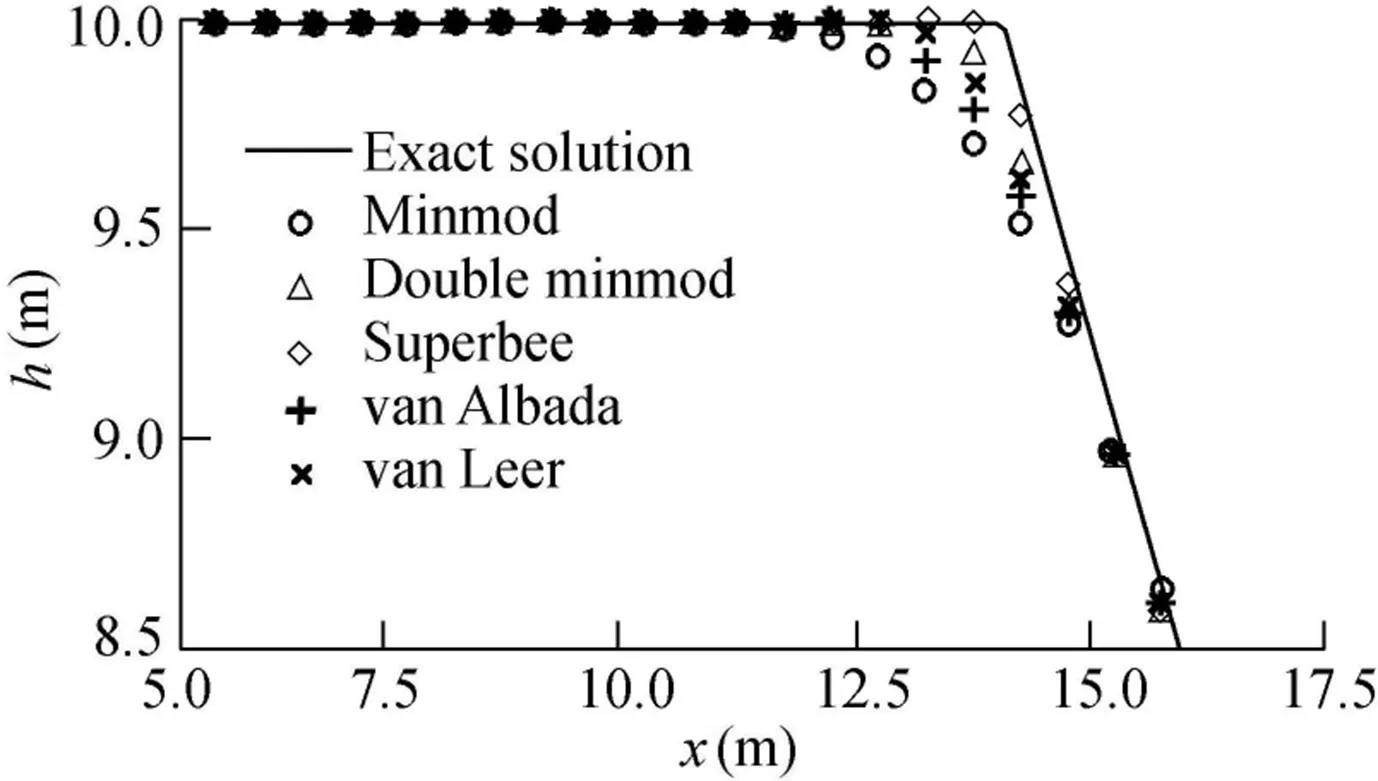
Fig.6.Comparison between exact solution and numerical solutions obtained from various limiters near first inflection point(x=14.0 m)at t=0.8 s with Ht/Hr=0.01.

The dry case at the right side of the dam was considered(Ht=0.0 m).At the initial time,the upstream water depth was 10 m.The computational space step was 0.25 m,and the time step was 0.01 s.Because of the limitation of the TVD scheme,it is difficult to accurately simulate the flow velocity when the water depth is shallow near the dry-wet front.Fig.8 shows the results of velocity whent=3.5 s.Fig.9 shows the results of partial amplification.It is demonstrated that the double minmod limiter gives a better result than others.

3.2.2D dam-break example

A 2D idealized circular dam with a horizontal bottom was considered.It is assumed that the dam is enclosed by an in finitely thin circular wall of radiusR=2.5 m in a square computational domain of 40 m×40 m with the center atxc=20.0 m andyc=20.0 m.At the initial time,the velocity both in thexdirection andydirection was zero throughout the domain.The water depth was 2.5 m inside the circular dam and 0.5 m in other areas.The value of Courant-Friedrichs-Lewy(CFL)coefficient was 0.9,and a mesh with 200×200 cells was used.

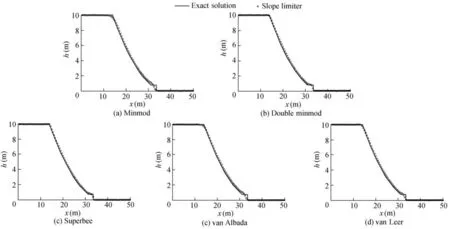
Fig.7.Comparison between exact solution and numerical solutions obtained from various limiters at t=0.8 s with Ht/Hr=0.001.

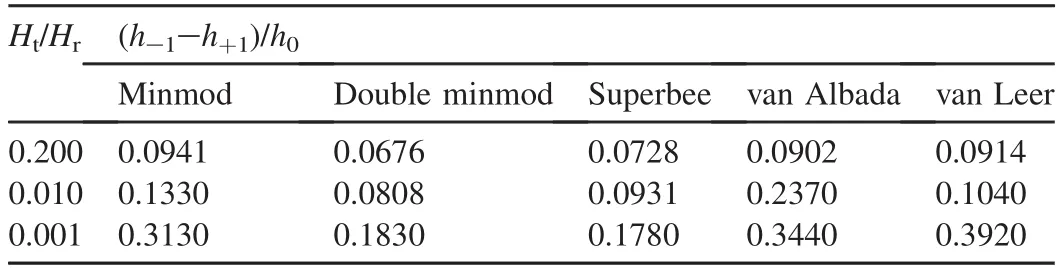
Table 1Results of parameter(h-1-h+1)/h0with five limiters at t=0.8 s.

The wave propagation phenomena associated with the sudden collapse of the entire wall was studied.Theoretically,the water waves should spread out in the form of concentric circles.Fig.10 shows the results of water depth contours with various limiters att=1.4 s.It is demonstrated that the superbee limiter has the most significant influence on the accuracy of the numerical model due to the significant numerical dispersion and other limiters give the similar results.

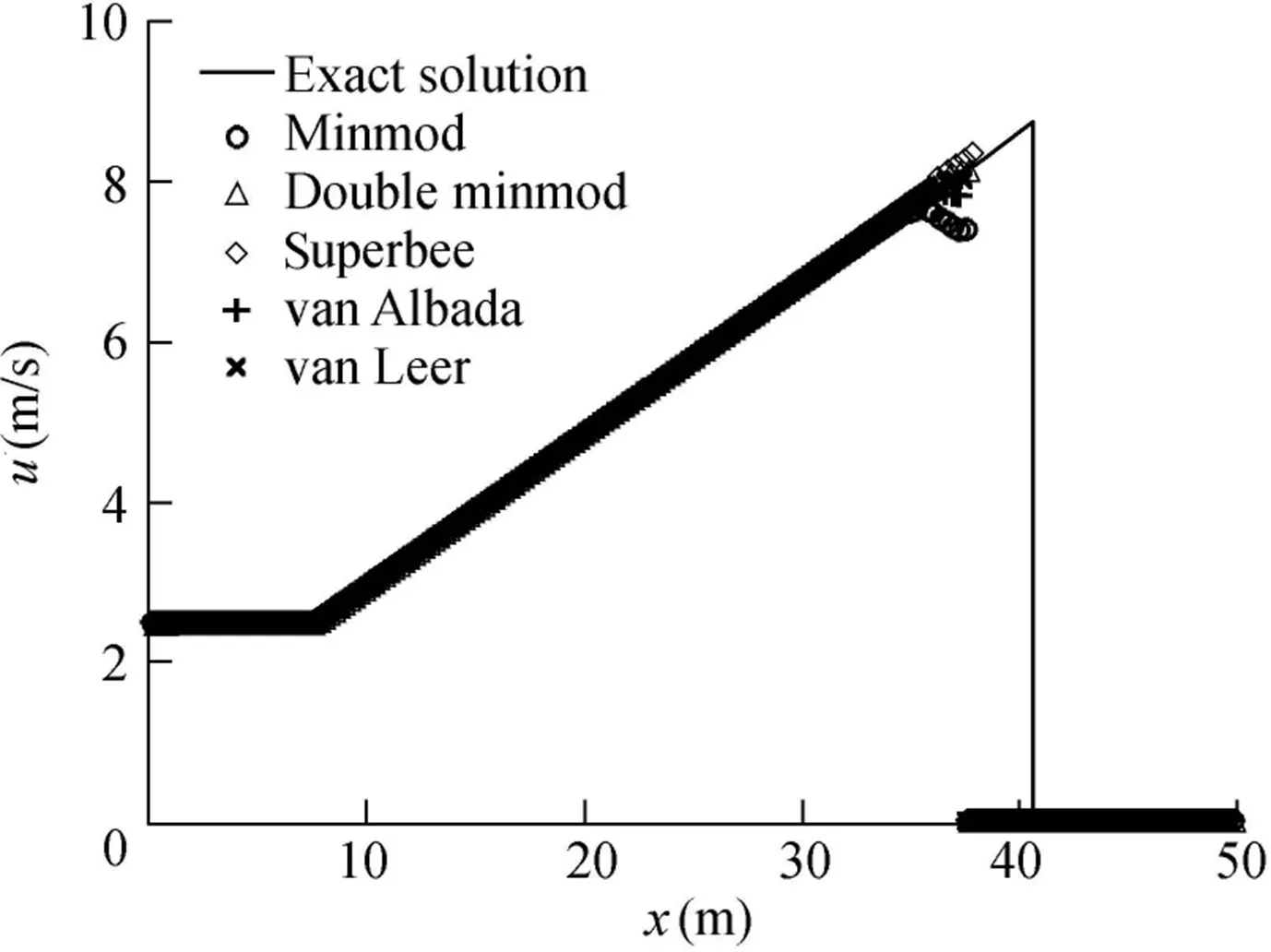
Fig.8.Comparative results at t=3.5 s with Ht=0.

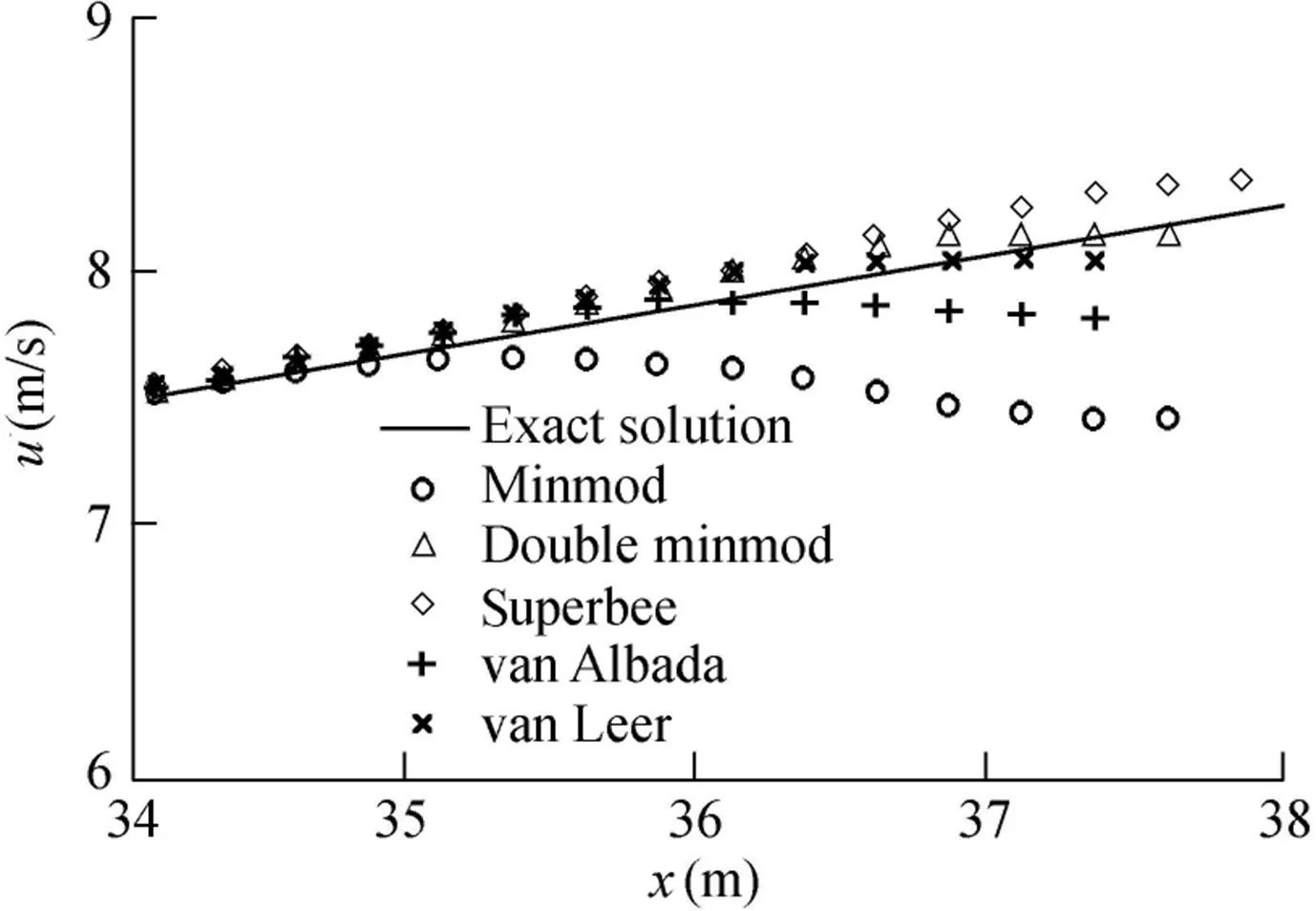
Fig.9.Partial zoom of Fig.8.

4.Conclusions

In this study,the effect of various slope limiters on the accuracy of a dam-break flow mathematical model was studied.In 1D space,the results of the superbee and double minmod limiters agree better with the exact solution.When the ratio of the downstream water depth to the upstream water depth is smaller than 0.01,the minmod,van Albada,and van Leer limiters fail to simulate the dam-break flow problems.The super bee limiter has the strongest ability to compress the waveform and turn the smooth wave into a square wave.Therefore,in 2D space,the super bee limiter can transform the wave near the discontinuity into a sawtooth-shaped wave.As a result,the superbee limiter causes significant numerical dispersion,and it was con firmed by the numerical experiment that the superbee limiter has the most significant impact on the accuracy of the numerical model.The appropriate limiter should be selected based on actual cases.In the future,research regarding the effect of various limiters on dam-break flow numerical models and considering the topographical and friction factors will be conducted.

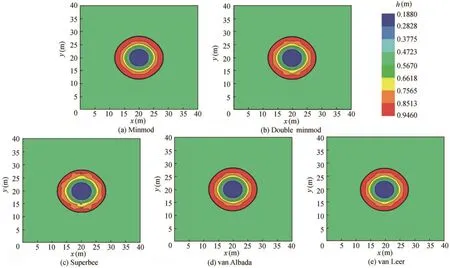
Fig.10.Results of water depth contour with five limiters at t=1.4 s.

References

Aliparast,M.,2009.Two-dimensional finite volume method for dam-break flow simulation.Int.J.Sediment Res.24(1),99-107.https://doi.org/10.1016/S1001-6279(09)60019-6.

Ata,R.,Pavan,S.,Khelladi,S.,Toro,E.F.,2013.A weighted average flux(WAF)scheme applied to shallow water equations for real-life applications.Adv.Water Resour.62,155-172.https://doi.org/10.1016/j.advwatres.2013.09.019.

Causon,D.M.,Ingram,D.M.,Mingham,C.G.,Yang,G.,Pearson,R.V.,2000.Calculation of shallow water flows using a Cartesian cut cell approach.Adv.Water Resour.23(5),545-562.https://doi.org/10.1016/S0309-1708(99)00036-6.

Erduran,K.S.,Kutija,V.,Hewett,J.M.,2002.Performance of finite volume solutions to the shallow water equations with shock-capturing schemes.Int.J.Numer.Meth.Fluid.40(10),1237-1273.https://doi.org/10.1002/fld.402.

Fraccarollo,L.,Capart,H.,Zech,Y.,2003.A Godunov method for the computation of erosional shallow water transients.Int.J.Numer.Meth.Fluid.41(9),951-976.https://doi.org/10.1002/fld.475.

García-Navarro,P.,V′azquez-Cend′on,M.E.,2000.On numerical treatment of the source terms in the shallow water equations.Comput.Fluids 29(8),951-979.https://doi.org/10.1016/S0045-7930(99)00038-9.

Harten,A.,Lax,P.D.,van Leer,B.,1983.On upstream differencing and Godunov-type schemes for hyperbolic conservation laws.SIAM Rev.25(1),35-61.https://doi.org/10.1137/1025002.

Kim,D.H.,Cho,Y.S.,Kim,H.J.,2008.Well-balanced scheme between flux and source terms for computational of shallow-water equations over irregular ba thy metry.J.Eng.Mech.134(4),277-290.https://doi.org/10.1061/(ASCE)0733-9399(2008)134:4(277).

Kim,H.J.,Cho,Y.S.,2011.Numerical model for flood routing with a Cartesian cut-cell domain.J.Hydraul.Res.49(2),205-212.https://doi.org/10.1080/00221686.2010.547037.

Liang,Q.,Borthwick,A.G.L.,Stelling,G.,2004.Simulation of dam-and dyke-break hydrodynamics on dynamically adaptive quadtree grids.Int.J.Numer.Meth.Fluid.46(2),127-162.https://doi.org/10.1002/fld.748.

Liang,Q.H.,2011.A structured but non-uniform Cartesian grid-based model for the shallow water equations.Int.J.Numer.Meth.Fluid.66(5),537-554.https://doi.org/10.1002/fld.2266.

Pu,J.H.,Cheng,N.S.,Tan,S.K.,Shao,S.D.,2012.Source term treatment of SWEs using surface gradient upwind method.J.Hydraul.Res.50(2),144-153.https://doi.org/10.1080/00221686.2011.649838.

Sanders,B.F.,Bradford,S.F.,2006.Impact of limiters on accuracy of highresolution flow and transport models.J.Eng.Mech.132(1),87-98.https://doi.org/10.1061/(ASCE)0733-9399(2006)132:1(87).

Sweby,P.K.,1984.High resolution schemes using flux limiters for hyperbolic conservation laws.SIAM J.Numer.Anal.21(5),995-1011.https://doi.org/10.1137/0721062.

Toro,E.F.,1999.Riemann Solvers and Numerical Methods for Fluid Dynamics:A Practical Introduction,second ed.Springer,Berlin.

Toro,E.F.,2001.Shock-capturing Methods for Free-surface Shallow Flows.John Wiley&Sons,Chichester.

van Albada,G.D.,van Leer,B.,Roberts,W.W.,1982.A comparative study of computational methods in cosmic gas dynamics.Astron.Astrophys.108(1),76-84.

van Leer,B.,1974.Towards the ultimate conservative difference scheme,II:Monotonicity and conservation combined in a second-order scheme.J.Comput.Phys.14(4),361-370.https://doi.org/10.1016/0021-9991(74)90019-9.

van Leer,B.,1979.Towards the ultimate conservative difference scheme,V:A second-order sequel to Godunov's method.J.Comput.Phys.32(1),101-136.https://doi.org/10.1016/0021-9991(79)90145-1.

Wu,W.M.,Marsooli,R.,2014.A depth-averaged 2D shallow water model for breaking and non-breaking long waves affected by rigid vegetation.J.Hydraul.Res.50(6),557-575.https://doi.org/10.1080/00221686.2012.734534.