ZHANG Liang,LU Yi,XU Shida,and FENG Han

Aeronautical Engineering College,Air Force Engineering University,Xi’an 710038,China

Abstract:To ensure multiple unmanned aerial vehicles(UAVs)reach stable formation quickly,a cooperative guidance law based on the back-stepping-like approach is designed in this paper.Adopting the guidance mechanism of virtue leader vehicle,the dynamic equation of tracking errors for each UAV is built.The communication interactive relationships are described based on graph theory,and the guidance law for formation reaching is obtained by the back-stepping-like approach.The formation stability is analyzed by constructing an appropriate Lyapunov function.The simulation results have shown that this guidance and control law can make each UAV converge to the trajectory of the virtue leader ultimately,and has the quicker rate of convergence and lower tracking error.

Keywords:unmanned aerial vehicle(UAV),formation reaching,guidance law,stability.

1.Introduction

Multi-unmanned aerial vehicle(UAV)formation flight control is a typical application mode for UAV systems[1,2],which has been a hot topic in current academic and military research.Multiple UAVs forming can significantly improve performance such as collaborative reconnaissance,tracking,and identification[3-6].Therefore,how to make the UAV in different initial positions rendezvous quickly,form a stable formation,and maintain the over all consistency,are the critical issues that the UAV collaborative control researcher need to solve.

In recent years,the relevant scholars have made extensive research from the theoretical and experimental point of view on the UAVs formation control issues.In[7-9],optimal control technique,navigation function and potential field method were used in solving the problem of formation control.In[10],the dynamic coupling characteristics of formation flight system were discussed,and the formation trajectory tracking controller was designed by the linear quadratic method.These methods usually have a high computational cost and are difficult to implement in a distributed manner.Therefore,stipanovic et al.used a distributed overlapping control technique to control a set of interconnected UAVs by designing a feedback controller for each UAV in the extended space which can convert it to the original space[11].Moreover,some scholars introduce predictive control methods to solve the formation control problem.The basic idea is to use the receding optimization method[12].In[13],the receding horizon control(RHC)method was used to study the high level formation control of UAV.In[14],a UAV formation control method based on hierarchical mechanism and model predictive control(MPC)strategy was proposed.The methodis more accurate,but the character of real-time is poor.Therefore,this paper proposes a back-stepping control method to design the law of formation control.Back-stepping technique is a nonlinear control technique proposed by Kokotovic[15]whose basic principle is firstly designing the desired virtual control input and then recursively feed backing it to the controller to get the actual control input.It can be used to design the controller by synthesizing the appropriate Lyapunov function.Compared with the linear feedback method,it has strong flexibility and does not require the linear closed-loop system.

The leader-follower method was applied in[16,17],where the first UAV is the leader and the others are the followers.It has simplified the multi-UAV control but there still exist some boundary.The West Virginia University proposed the virtual leader method[18,19],where all UAVs are considered into a whole rigid body.Each UAV only has to track the fixed point of the rigid body.Brad et al.studied this problem using the behavior control method and proposed the concept of Formation Geometry Center[20].

This paper takes the virtual lead aircraft guiding UAVs formation as the task scene.Firstly,the dynamic error model of each UAV’s position relative to the virtual leader is established.And the communication between UAV and the virtual leader is established by the graph theory.Secondly,the paper uses the back stepping-like method to design the synergetic guidance law of formation control and analyze its stability.Finally,the validity of the method is verified by constructing the simulation.

2.Problem description and modeling

Considering a scenario in which multiple UAVs form a formation by a virtual leader.Each UAV from different initial positions,tracking virtual leader flight path,quickly forms and maintains the formation.To achieve this goal,firstly a suitable UAV motion model need to be established,which accurately describes the communication interaction between UAVs.

2.1 UVA motion modeling

In general,assume the velocity vector vgis perpendicular to the speed of the UAV,the longitudinal axis of the body,the resistance and the thrust on the same straight line,and the lift as shown in Fig.1.Using the UAV particle model with three degrees of freedom,it is assumed that velocity,track angle and heading angle are first-order dynamic models.According to[21-24],the equations of motion are shown as

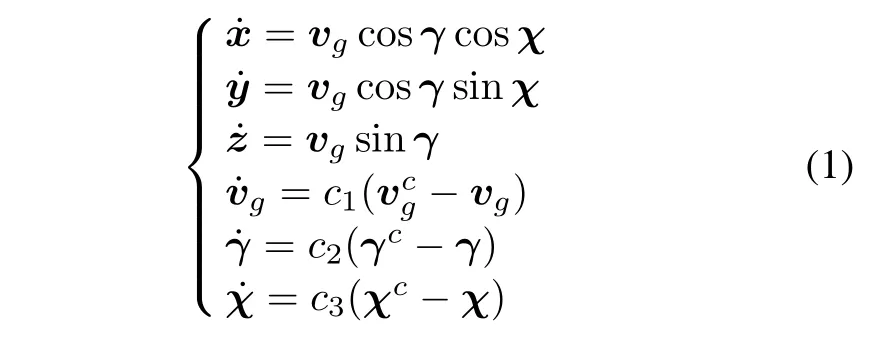
where(x,y,z),vg,χ and γ represent the position,velocity,heading angle and track angle of UAV in inertial coordinates,respectively.c1,c2and c3(c1＞0,c2＞0,c3＞0)are time constants,respectively.,γcand χcrespectively are the command speed,track angle and heading angle.

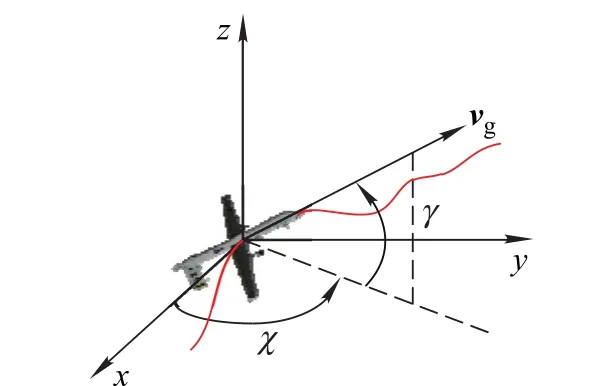
Fig.1 Sketch map of UAV three dimensional motion

For the virtual leader,the five-variable state UAV model in[25]is adopted,but the first-order dynamic model is still used.At this point,the virtual machine’s equations of motion are shown as

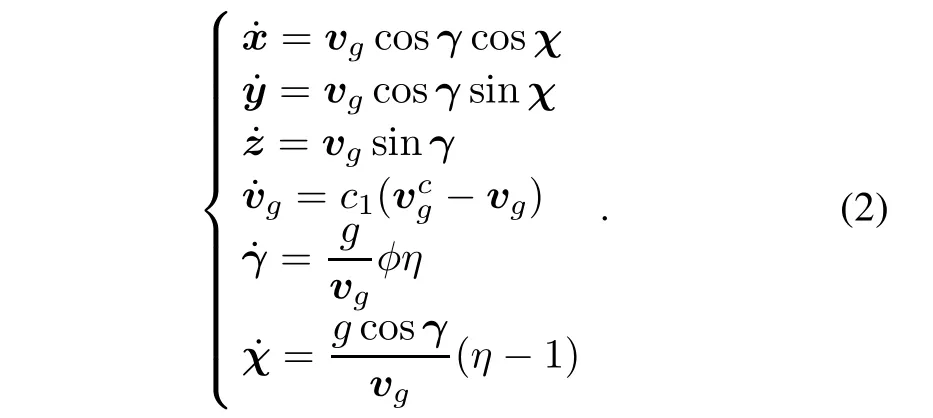
where,χ is heading angle,γ is track angle,g is gravity acceleration,φ is roll angle,η is overload factor.Then,through the geometric relationship,the above formula is transformed into

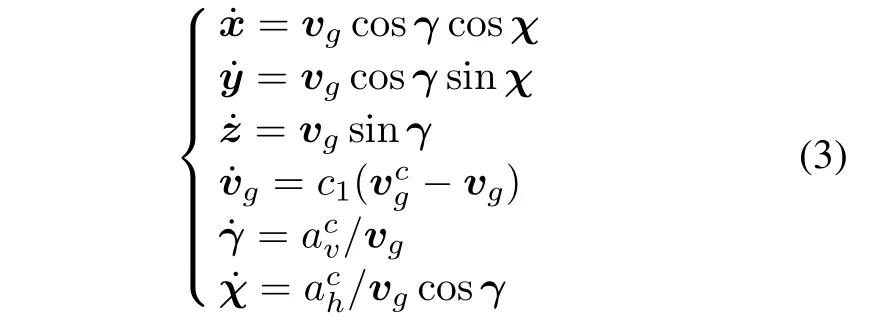
2.2 UAV communication interaction modeling

Considering a UAVs network system,the local communication relationship between the UAVs is represented by a dynamic graph G(t).Considering a dynamic graph G(t)=(V,E(t)),V is a nonempty finite set V={1,2,...,n},E(t)is a set of edge.E?V×V.Each UAV can be represented as a node,and their interaction is represented by an edge.The adjacency matrix is used to represent the interaction between the UAVs.Then,the adjacency matrix of graph G can be expressed as A=[aij],while aijis the weight of the graph,satisfying

Here,edge eij=(vi,vj)represents that node vican obtain information from node vj.Thus,node viis considered to be the child node,and vjis its father node.The neighbor set of node vjcan be represented by set Nj={vi:(vi,vj)∈E}.At the same time,the diagonal matrix D(t)=[dij]is defined,and the diagonal elements are the sum of the row elements of the matrix A,,which presents the number of neighbors of the node vi,which is also called in-degree.

Assume that the virtual leader is embedded in a subset of the network.Here,the reference track information of the virtual leader at least one node in the network is available.The connectivity of the network is represented by matrix B,defined as B=[bij].This is a diagonal matrix whose diagonal elements biiare traction gain and there is at least one node’s bii＞ 0.

3.Cooperative formation guidance law

For each UAV,the desired dynamic equation is

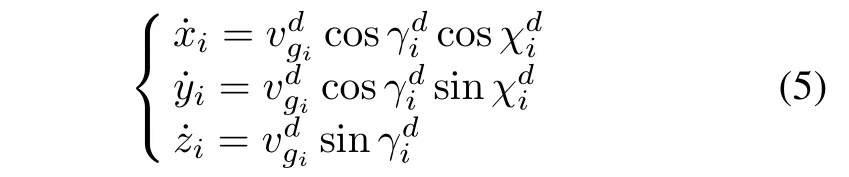
Define the tracking error for each UAV as follows:

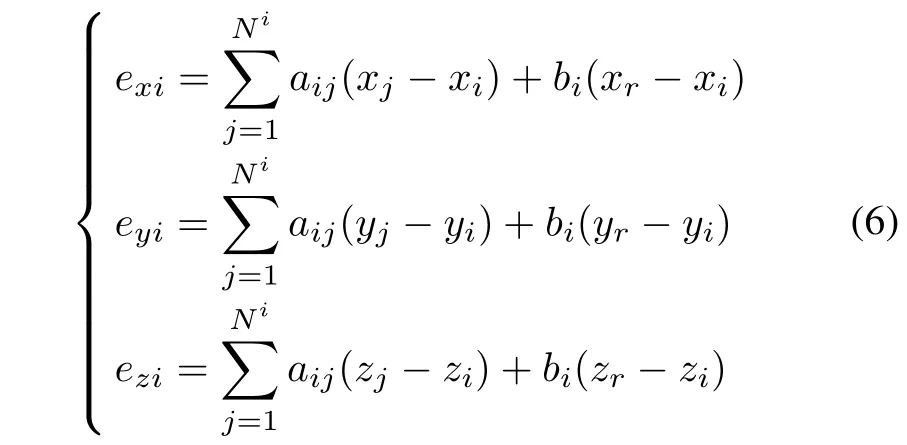
where i∈{1,2,...,N}.Based on the matrix theory,the above formula is transformed into the following form:

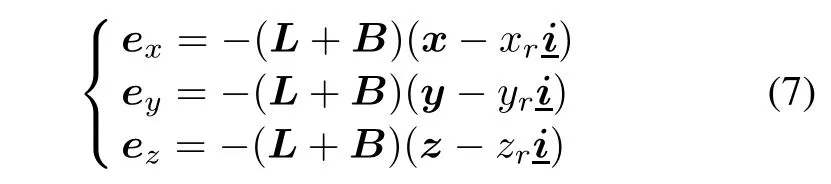
whereL=[lij]is the Laplacian matrix,and L=(D-A),i is the unit vector of N×1.

Then,(7)can be obtained,the following compact form of the error dynamic equation is

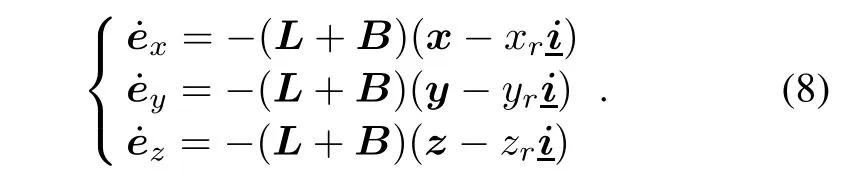
Assuming that the error equation is integrated at each position channel as=ux,=uyand=uz.Based on local feedback,the control law for the following position tracking is available:

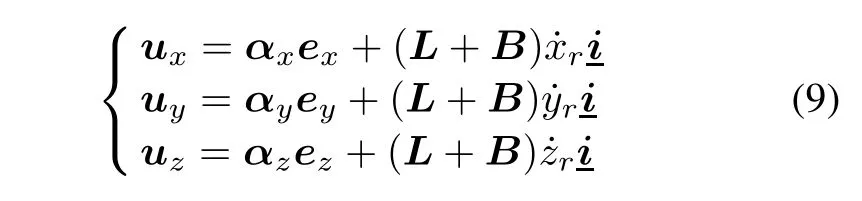
where αx,αyand αzare respectively the diagonal positive definite gain matrices of the appropriate dimension.

It can be deduced that if the graph is highly connected,theL+B is the positive definite matrix.Here,the expected value is

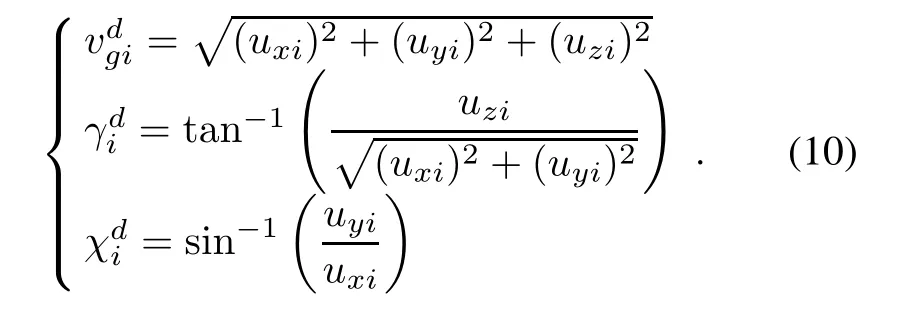
Define the errors of vg,γ and χ as

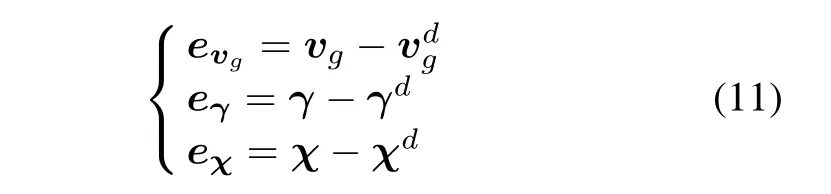
where vg=[vg1,vg2,...,vgN]T,γ =[γ1,γ1,...,γN]T,χ =[χ1,χ2,...,χN]T.

To ensure that the designed control law is convergent,the following error equation is given,according to the exponential convergence function:

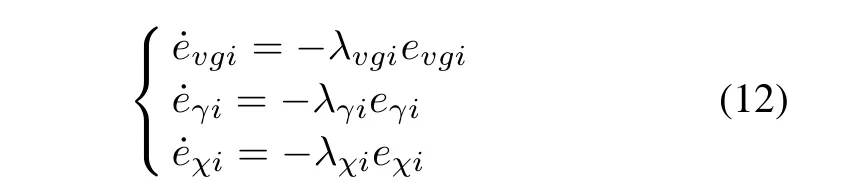
whereλvgi,λγiandλχiare the specified positive numbers.The derivatives of,andare

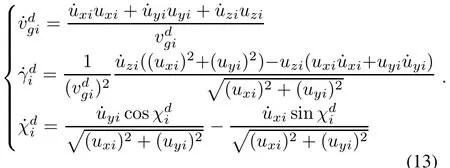
As can be seen from(13)that the derivatives ofandneed the derivative of the control signal from the position control loop.That is the derivative of uxi,uyiand uzi.Taking the derivative of(9),

It should be noted that the implementation of position tracking control loop requires uxi,uyiand uzi.To achieve speed level tracking requires derivatives of uxi,uyiand uzi.And the tracking scheduled reference trajectory control law can be obtained in accordance with the position variable.If the expected velocity,path angle and heading angle variable are consistent,the expected dynamic equation of(12)can be improved to

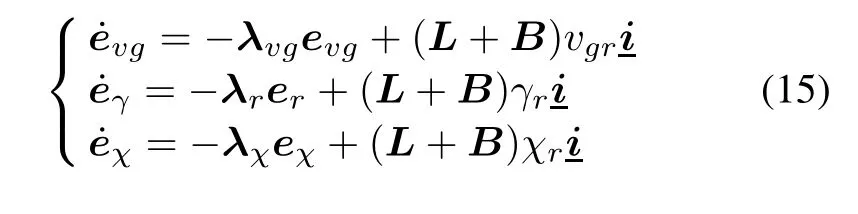
where λvg,λγand λχare diagonal positive definite gain matrices.Jointing(1)and(15),the covariance control law is

4.Stability analysis

To prove the closed-loop stability of the whole system,select the Laypunov function like

Taking the time derivative of W:

Jointing(15),(8)and(9),the time derivative of the Lyapunov function is given by

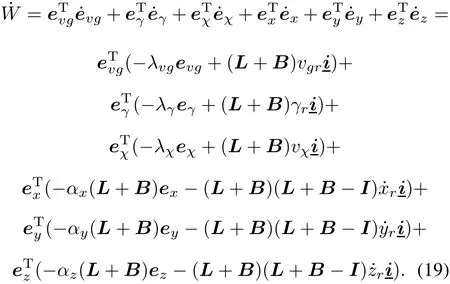
According to the related theorem of graph theory,if a graph has a directed spanning tree,the correlation matrix(L+B)is a positive definite matrix.If the minimum and maximum singular values of the matrix(L+B)are represented byandrespectively,represent the minimum ofrepresent the minimum of αx,αy,αz,then

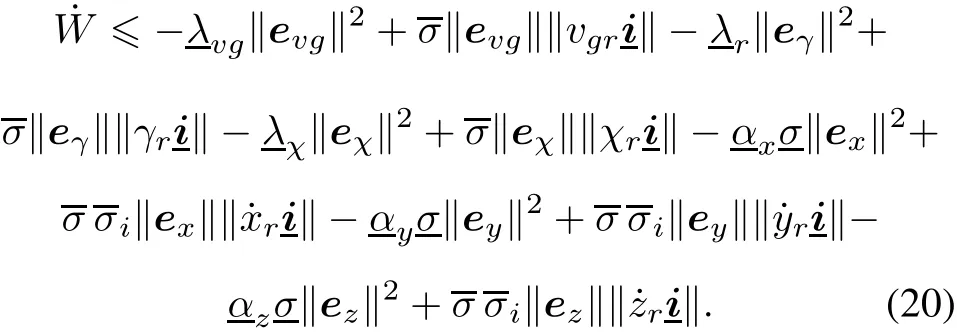
Note that the reference trajectory is bounded,which is

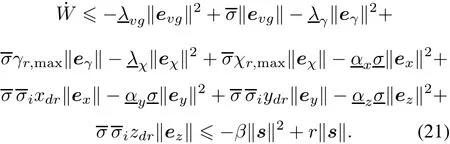
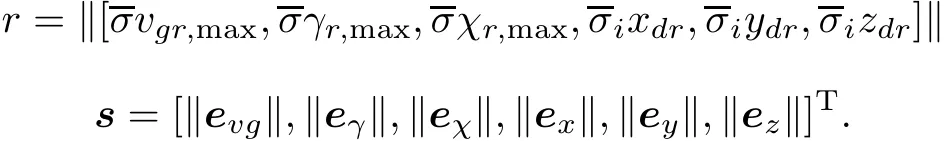
Obviously,the derivative form of the Lyapunov function is given by

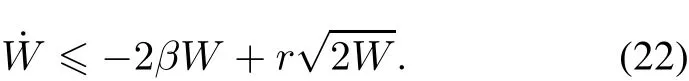
Thus,

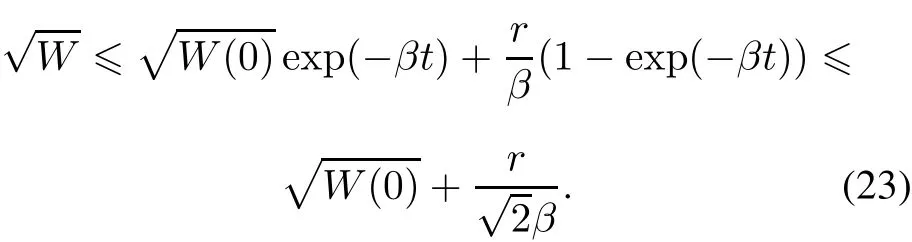
Therefore the conclusions are

(i)If xr,yr,...=constant,r=0,the graph has a directed spanning tree,and all UAVs in the formation can achieve the same consistency.

(ii)If the desired reference state is constant and there is at least a second derivative,the trajectory tracking error is bounded.Using a large control gain β,the tracking error can be arbitrarily small.

(iii)The system is asymptotically stable if it includes a directed graph with spanning tree,and the state and its second derivative are uniformly bounded at least so that all tracking errors are uniformly bounded.

At this point,according to the above three conclusions,the stability of the guidance system designed in this paper is vertified.

5.Simulation analysis

In order to verify the validity of the guidance law of the UAVs coordinated fleet designed in this paper,the simulation environment is built based on Matlab Simulink.All the calculations are operated in a computer,with Intel Core I5 CPU,clocked at 2.8 Ghz,Windows operating system.

Consider a multi-UAV system with three UAVs as shown in Fig.2.The communication network graph is a strongly connected graph,assuming that the virtual leader is embedded in the subset of the graph UAV1,then the adjacency matrix A,Laplacian matrix L,traction matrix B and diagonal matrix D are respectively

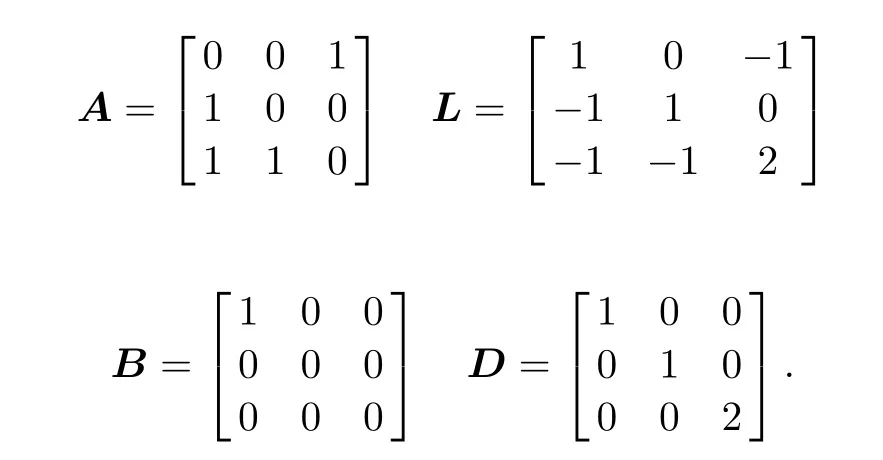
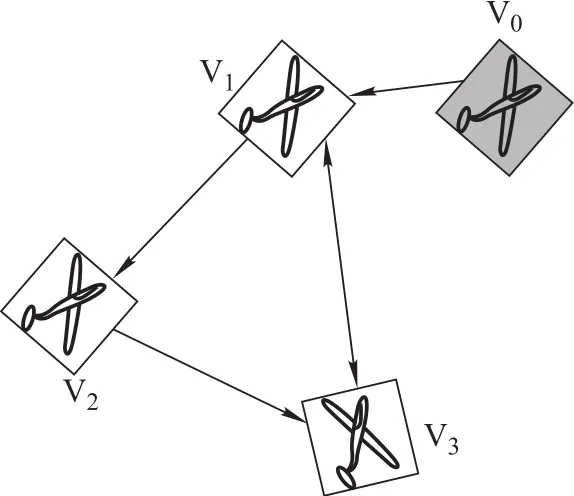
Fig.2 Communication topology of formation control

In the simulation,the initial conditions of each UAV are shown in Table 1,the virtual leader vehicle’s other parameters of the initial value of(0)=12 m/s,(0)=0.2 m/s2,(0)=0.2 m/s2.Meanwhile,the actuator constant and control gain of the three UAVs are:c1=c2=c3=10,α1= α2= α3=2,λvg= λγ=2,λχ=2.

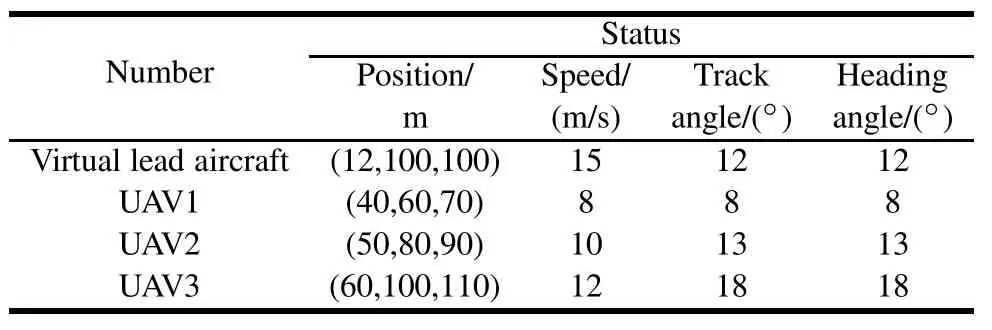
Table 1 Initial conditions of each UAV

Simulation results are shown in Figs.3-5.From the figures,it is clear that from the different initial positions of the three UAVs,under the guidance of the virtual lead aircraft,their relative positions and tracking errors constantly change with time.After about 3 s,UAVs converge to the flight path of the virtual leader vehicle,and eventually reach the consistency of position and speed,thus forming a stable formation.

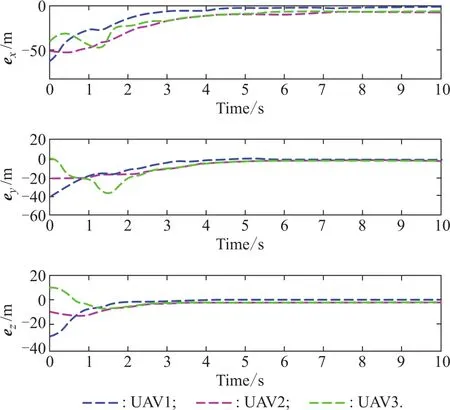
Fig.4 Change curve of positions tracking error

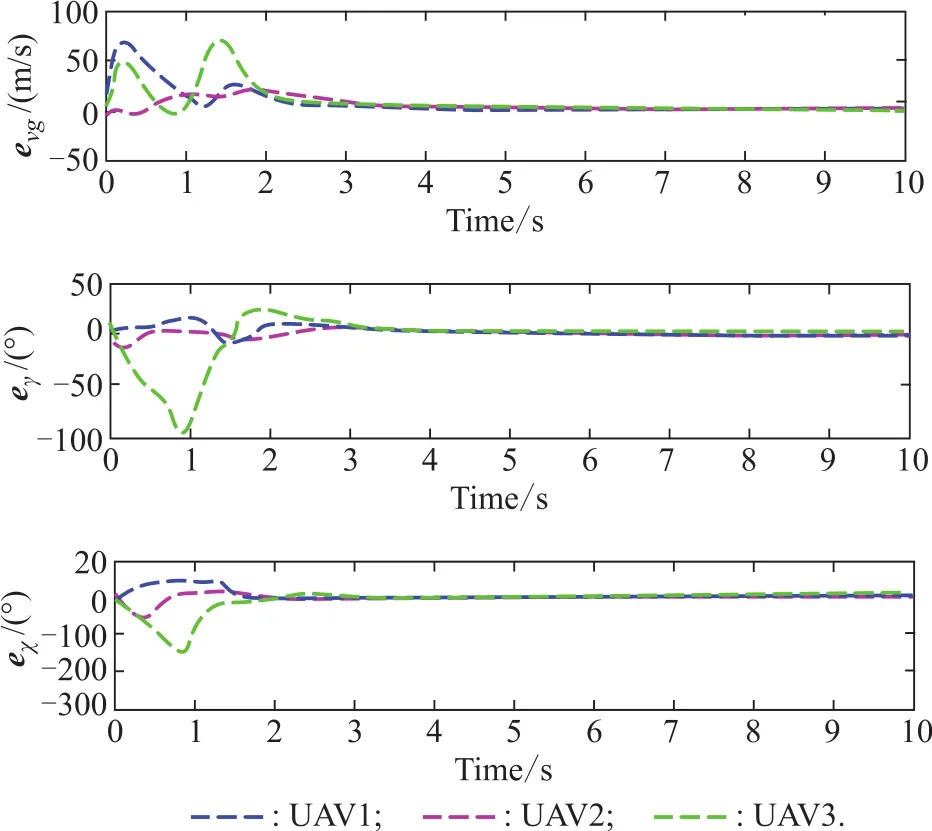
Fig.5 Change curve of control inputs tracking error

In order to further verify the advantages of the formation of the guidance system in the convergence rate and tracking error,the optimal control method and the MPC method are used to simulate the simulation under the same initial conditions.It can be observed from Fig.4 and Fig.5 that the position tracking error and the control input tracking error of UAV3 change with time while the stable formation is formed.Therefore,in order to make the comparison results more representative,UAV3 tracking virtual is taken leader as an example to verify the three methods in the position tracking error comparison shown in Fig.6.

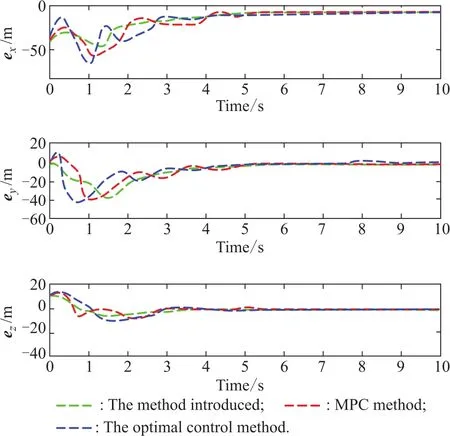
Fig.6 Comparison of three methods on position tracking error

It is clear that,using these three methods,UAV3 can eventually converge to the flight path of the virtual leader,but the time required is not the same.The convergence of the MPC method is the longest while the error fluctuation is less than the optimal control method.The convergence time of the optimal control method is shorter than that of the MPC method,its error fluctuating is larger however.The method introduced in this paper is superior to the optimal control method and the MPC method in terms of convergence rate and tracking error.

5.Conclusions

In this paper,the steering system is constructed based on the back-stepping control method of UAVs,and its convergence is proved by Lyapunov stability theorem.Compared with the optimal control and the MPC method,this method can form a stable multi-machine formation with faster convergence rate and smaller tracking error.It has guiding significance to coordinate multiple UAVs to a rapid combat formation in the battle field.