LIN Xiaoyan,CHEN Lingmei,LIN Dongyun,and LAN Weiyao

Department of Automation,Xiamen University,Xiamen 361005,China

Abstract:Composite nonlinear feedback(CNF)control technique for tracking control problems is extended to the output regulation problem of singular linear systems with input saturation.A state feedback CNF control law and an output feedback CNF control law are constructed respectively for the output regulation problem of singular linear systems with input saturation.It is shown that the output regulation problem by CNF control is solvable under the same solvability conditions of the output regulation problem by linear control.However,with the virtue of the CNF control,the transient performance of the closed-loop system can be improved by carefully designing the linear part and the nonlinear part of the CNF control law.The design procedure and the improvement of the transient performance of the closed-loop system are illustrated with a numerical simulation.

Keywords:singular linear system,input saturation,output regulation,composite nonlinear feedback.

1.Introduction

Singular systems,also known as descriptor systems or differential-algebraic systems,arise in various practical systems such as large-scale networks,chemical engineering systems,and electrical and mechanical systems[1,2].In recent two decades,singular systems subject to input saturation are investigated in the literature,such as stabilization problems[3-5]and output regulation problem[6,7].

The output regulation problem is to design a control law such that the output of the closed-loop system converges to zero asymptotically while maintaining the stability of the closed-loop system.As a fundamental problem in control theory,output regulation problems are extensively studied in the literature for both linear systems and nonlinear systems,see,e.g.,[8]and the references in it.Besides for normal systems,the output regulation problems for singular systems also attract much attention in recent years.The solvability conditions for the output regulation problem of singular linear systems were established in[9].After that,the output regulation problems for singular nonlinear systems are addressed in[10],[11],and[12],etc.For the singular linear systems with input saturation,the semiglobal output regulation problem was investigated by[6].It should be noted that these results on output regulation problems of singular systems focus on the solvability conditions of the regulation problems,i.e.,steady state solutions.The results on addressing the transient performance of the output regulation problems are quite limited.For this reason, we introduce the so-called composite nonlinear feedback (CNF) control technique for the output regulation problem of singular linear systems with input saturation to improve the transient performance of the closed-loop system.

The CNF control technique was firstly proposed in[13]to improve the transient performance for the tracking control problem of a second-order linear system with input saturation.The CNF control law consists of two parts,a linear part and a nonlinear part.The linear part is designed to yield a closed-loop system with a small damping ratio such that the output response has a fast rise time.The nonlinear part is introduced to increase the damping ratio of the closed-loop system to reduce the overshoot caused by the linear part.For more general systems,Chen et al.developed a CNF control method for general linear systems with input saturation[14].The CNF control technique is extended to a class of nonlinear systems in[15]and[16].Moreover,a structural design method for CNF control law was proposed by[17].Besides the development in theory,the CNF control is successfully applied to design various servo systems,such as hard disk drive(HDD)servo systems[14,18],helicopter flight control systems[19],position servo systems[20],path following of autonomous ground vehicles and surface vessels[21,22],and control of multiple quadrotors[23,24].Also,the CNF control is successfully introduced to solve the out put regulation problem of linear systems with input saturation and to improve the transient performance of the closed-loop system,see,e.g.,[25],[26]and[27].Recently,the CNF control technique was extended to singular linear systems with input saturation for tracking control problems by[28]and[29].Yu et al.extended the result of[28]to a class of multi-variable discrete-time singular linear systems[30].

Based on the recent work on CNF control[26,28],this paper investigates the output regulation problem of singular linear systems with input saturation by the CNF control method to address the transient performance improvement.In the framework of the output regulation problem which integrates tracking control problems and disturbance rejection problems,the tracking reference or the disturbance can be constant signals and/or time-varying signals.Comparing with the tracking control problem of singular linear systems in[28]and the output regulation problem of normal linear systems in[26],the construction of the CNF control law is quite different and more dif ficult in technique which makes the work of this paper more challenging and more interesting.Specifically,we will design a state feedback CNF control law and an output feedback CNF control law to solve the output regulation problem of singular linear systems with input saturation.With the structure of the CNF control law,not only the steady state performance of the closed-loop system is addressed by establishing the solvability conditions of the output regulation problem,but also the transient performance of the closed-loop system can be improved by tuning carefully the linear part and the nonlinear part of the CNF control law.

The contribution and novelty of this paper can be described in two folds.First,it is an extension of the work of[28]in which the tracking control of singular linear systems with input saturation by composite nonlinear feedback control is investigated.It should be noted that only the tracking control problem was addressed in[28],and the tracking targets in[28]were some constant step functions.Since both the tracking control problem and the disturbance rejection problem can be formulated as the output regulation problem,the proposed CNF control method can be applied to improve the transient performance of the closed-loop system for the tracking control problem and disturbance rejection problem.Moreover,in the framework of the output regulation problem,the tracking reference and the disturbance are described with a dynamic exo-system,the tracking reference and disturbance can be time-varying.Second,it is also an extension of the work of[26]in which the transient performance improvement by CNF control is investigated for the output regulation problem of linear systems with input saturation.Though the design procedure of the CNF control law is quite similar with[26],the CNF controller design for output regulation problem of singular linear systems is much more difficult than the normal linear system case.And,it is more challenging to establish the stability of the closed-loop system for singular linear systems.

The remainder of the paper is organized as follows.Section 2 describes the output regulation problems of singular linear systems with input saturation.A state feedback CNF control law and an output feedback CNF control law are designed respectively to solve the output regulation problem in Section 3 and Section 4.In Section 5,the design procedure is illustrated,and the improvement of the transient performance is shown with an example of a disturbance rejection problem.

2.Problem formulation

Consider a linear system with input saturation as follows:

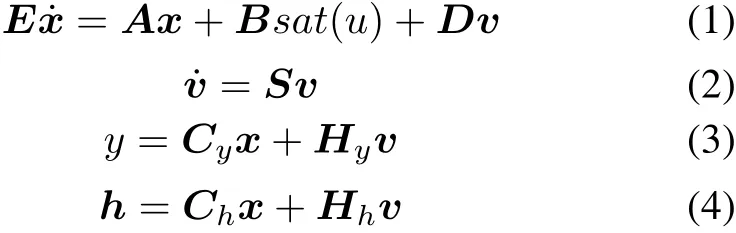
where x∈Rnis the state,u∈R is the control input,v∈Rmis the exogenous signal representing the disturbances and/or the reference input,y∈R is the controlled output and h∈Rpis the measurement output.E,A ∈Rn×n,B ∈ Rn×1,D ∈ Rn×m,S ∈ Rm×m,Cy∈ R1×n,Ch∈ Rp×n,Hy∈ R1×mand Hh∈ Rp×mare constant matrices.Without loss of generality,we assume that E is singular and(E,A)is regular.And sat(u):R→R represents the actuator saturation defined as

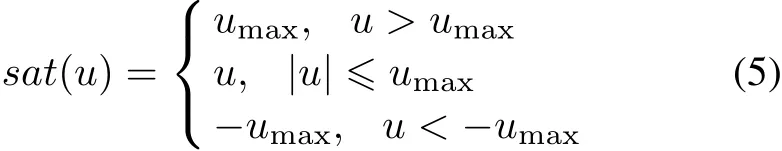
where umaxis the maximum of the control input.We will consider the following output regulation problems for the singular linear system(1)-(4).

The output regulation problem by state feedback CNF control:consider the singular linear system(1)-(3),and design a state feedback CNF control law in the form of

and find some compact sets X0?Rnand V0?Rmcontaining their origin respectively,such that the closed-loop system satisfies the following requirements:

Requirement 1 When v=0,the equilibrium point x=0 of the closed-loop system is asymptotically stable for x(0)∈X0;

Requirement 2 For all(x(0),v(0))∈X0×V0,the solution of the closed-loop system satisfies

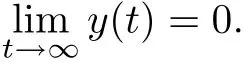
The output regulation problem by output feedback CNF control:consider a singular linear system(1)-(4),and design an output feedback CNF control law in the form of

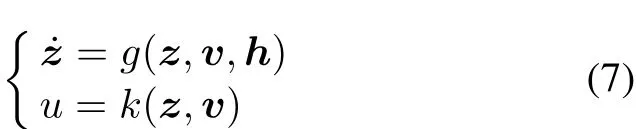
where z∈Rn-p, find some compact sets X0?Rn,Z0?Rn-pand V0?Rmcontaining their origin respectively,such that the closed-loop system satisfies the following requirements:

Requirement 3 When v=0,the equilibrium point(x,z)=(0,0)of the closed-loop system is asymptotically stable for all x(0)∈X0and z(0)∈Z0;

Requirement 4 For all(x(0),z(0),v(0))∈X0×Z0×V0,the solution of the closed-loop system satisfies

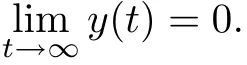
Remark 1 The state feedback control law(6)solves the output regulation problem of the system(1)-(4)if the closed-loop system under the state feedback control law(6)satisfies Requirement 1 and Requirement 2.Similarly,if the closed-loop system under the output feedback control law(7)satisfies Requirement 3 and Requirement 4,the output feedback control law(7)solves the output regulation problem of the system(1)-(4).In this paper,only local output regulation problems are considered,thus,X0in Requirement 1(or X0and Z0in Requirement 3)can be arbitrary small.The solvability conditions are established for the state feedback output regulation problem and the output feedback output regulation problem in Theorem 1 and Theorem 2 respectively.An X0in Requirement 1 is specified in Theorem 1 for the state feedback output regulation problem,and a pair of X0and Z0in Requirement 3 are specified in Theorem 2 for the output feedback output regulation problem.

Before establishing the solvability conditions for the above-defined output regulation problems,we list the following standard assumptions for the output regulation problems of singular linear systems.

Assumption 1 rank[sE-A B]=n for all s∈C+,s finite,where C+represents the closed right half complex plane.

Assumption 3 All the eigenvalues of S are simple and on the imaginary axis.

Assumption 4 There exist two matrices Π ∈ Rn×mand Γ ∈ R1×mthat solve the following singular regulator equations:

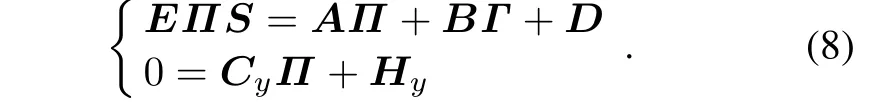
Remark 2 Without considering the input constraint,the output regulation problem of linear singular system was studied in[9].Under Assumptions 1,3 and 4,a linear state feedback control law that solves the output regulation problem is given by

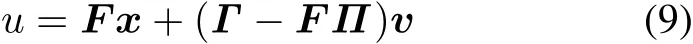
where F is an arbitrary matrix such that the singular system(E,A+BF)is stable,and Γ and Π are the solutions of the regulator equations(8).Assumption 2 guarantees that there exists an F such that the singular system(E,A+BF)is impulsive free.Assumptions 5 and 6 are needed to design an output feedback control law.

3.CNF control by state feedback

In this section,we present the construction of a state feedback CNF control law,and show how it solves the output regulation problem of the system(1)-(3).The CNF control law is combined by a linear part and a nonlinear part.We design the linear part to solve the output regulation problem with a fast dynamic response.However,it often causes a large overshoot.Thus,the nonlinear part is introduced to reduce the overshoot.The CNF control law can be established by the following steps with Assumptions 1-4.

Step 1 Design a linear state feedback control in the form of

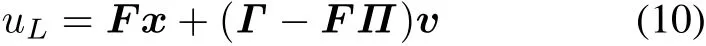
where Π and Γ are the solutions of the regulator equation(8)in Assumption 4.And F is selected such that

Property 1 σ(E,A+BF)? C

Property 2 deg(det(sE-(A+BF)))=rankE whereσ(E,A+BF)={s|s∈C,det(sE-A-BF)=0},and C-={s|s∈C,Re(s)＜0}.Such an F exists because of Assumptions 1 and 2.

Step 2 The nonlinear part of the CNF control law is given by

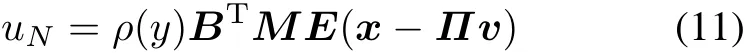
where ρ(y)is a non-positive function locally Lipscitz in y,M＞0 is the solution of the following generalized Lyapunov equation:for some W＞0.

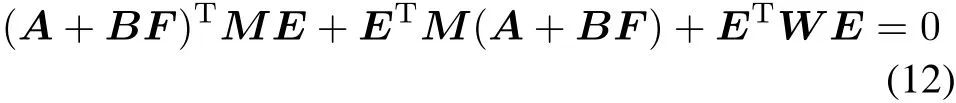
Step 3 Combining the linear and nonlinear parts,the state feedback CNF control is obtained as

The following theorem presents the solvability conditions for the output regulation problem by the CNF control law(13).

Theorem 1 Consider the given system(1)-(3)with Assumptions 1-4,and the CNF control law(13).For a given σ ∈ (0,1),let cσbe the largest scalar such that

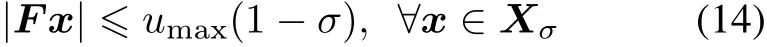
with

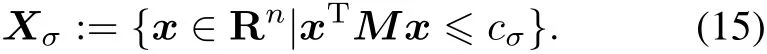
For any non-positive function ρ(y)locally Lipschitz in y,the state feedback control law(13)solves the output regulation problem if the initial states x0and v0satisfy the following conditions:

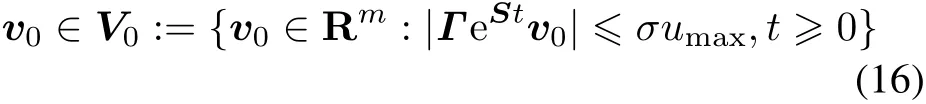
and

Proof Let

and note that

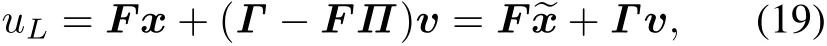
the closed-loop system can be written as

where

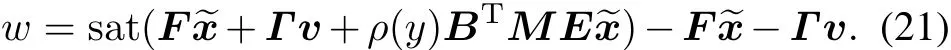
Define a Lyapunov function as follows:

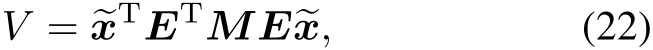
then

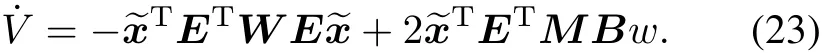
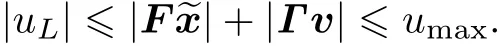
Thus,it is not difficult to deduce that

Case 1 If|u|?umax,then

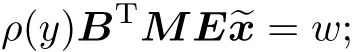
Case 2 If u＞umax,then

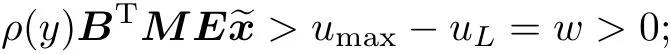
Case 3 If u＜-umax,then

From above,we can express w as

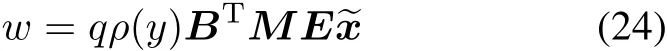
where q(t)∈[0,1]is a piecewise continuous function.Then

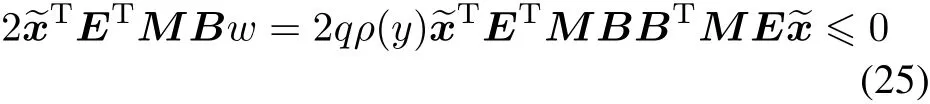
because of ρ(y)?0.Thus we have

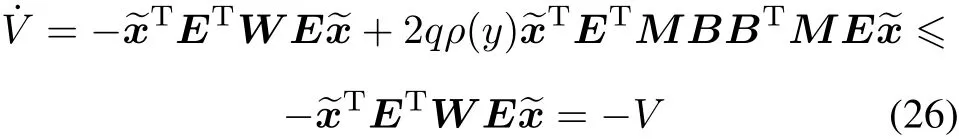
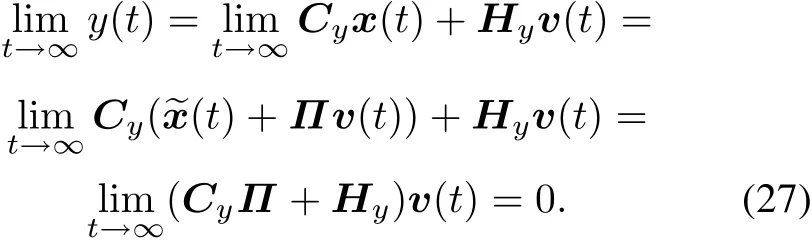
Thus Requirement 2 is also satisfied.This completes the proof of Theorem 1. ?

Remark 3 Theorem 1 establishes the solvability conditions of the output regulation problem by state feedback CNF control.Theorem 1 is proved by showing that Requirement 1 and Requirement 2 are satisfied when the system(1)-(4)is controlled by the state feedback CNF control law(13).As the extension of[26]and[28],the solvability conditions described by Theorem 1 covers the results of[26]and[28].In fact,if E =I in(1),i.e.,the system is reduced to a normal linear system,Theorem 1 is equivalent to Theorem 3.1 of[26].On the other hand,if the exo-system is given by=0,v(0)=r,Theorem 1 covers Theorem 4.1 of[28].Moreover,if E=I and=0,v(0)=r,Theorem 1 can be reduced to the result of[14].

4.CNF control by output feedback

If the states of the singular linear system is not available for feedback control,we can establish an output feedback control law based on a linear reduced-order state observer to solve the output regulation with additional Assumptions 5 and 6.

Firstly,we need design an observer to estimate the states.Considering the system(1)-(4),we can easily know that there exist nonsingular matrices P and Q such that

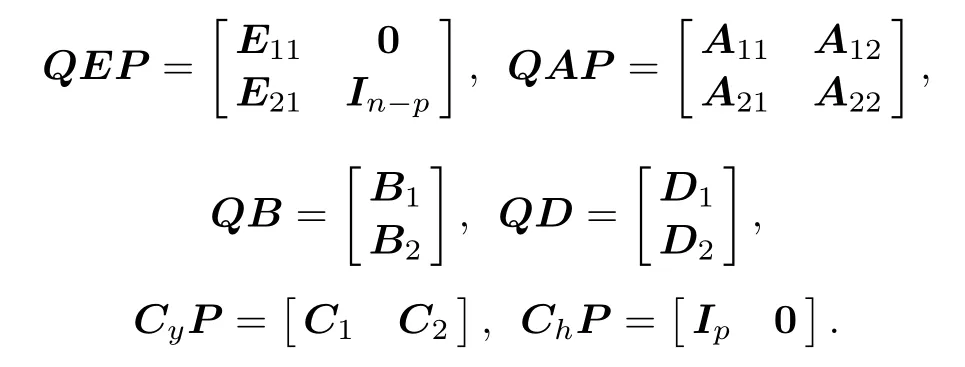
Thus,under the cordinate transformationsystem(1)-(4)is a restricted system equivalent to

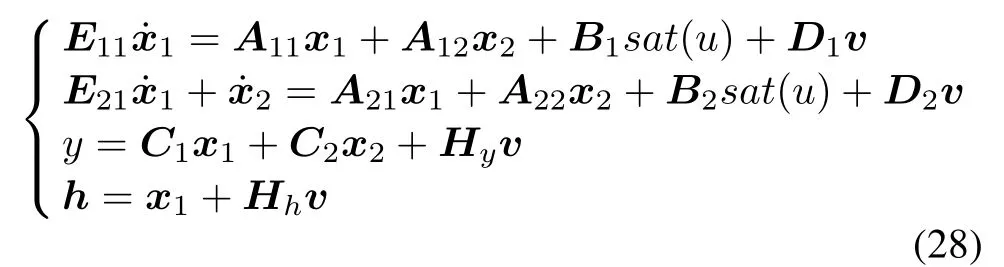
where x1∈Rp,x2∈Rn-p.

From(28)we see that the substate x1may be obtained directly from measure output h(t)and exogenous signal v(t),and the substate x2satisfies the following dynamic equation:

Moreover,since system(1)-(4)is assumed to be detectable,we have

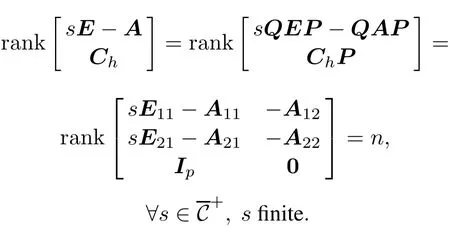
Therefore,

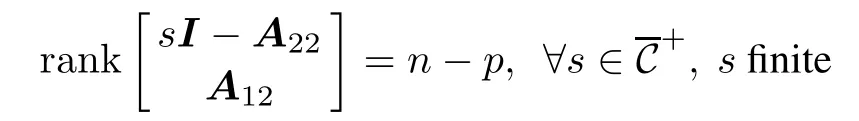
which means(A22,A12)is detectable.Then,there exists a matrix K ∈ R(n-p)×psuch that σ(A22-KA12)? C-.Thus,the system(29)has the following state observer:

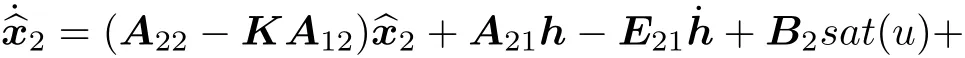
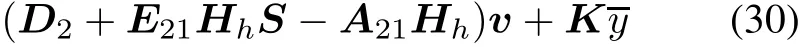
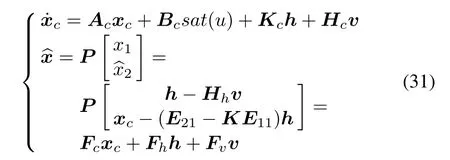
where

Combining the above state feedback CNF control law(13)and the nonsingular linear reduced-order observer(31),the output feedback CNF control is obtained as

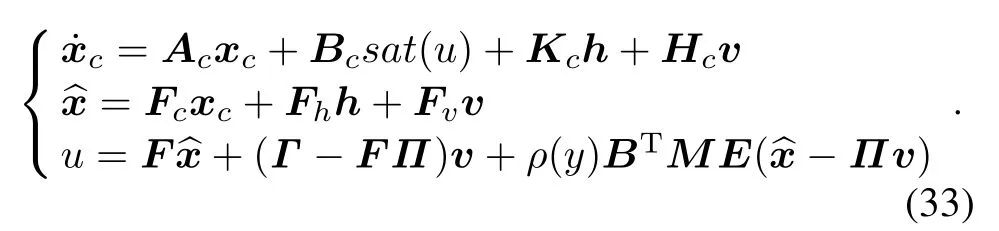
The following theorem presents the solvability conditions for the output regulation problem by the CNF control law(33).

Theorem 2 Consider the given system(1)-(4)with Assumptions 1-6.Given a positive-definite matrix WR∈R(n-p)×(n-p)such that

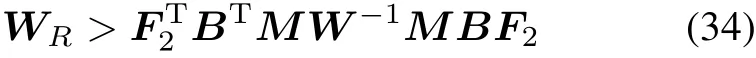
where F2∈ R1×(n-p)is defined by FP=[F1F2].Let R＞0 be the positive definite solution of the following Lyapunov equation:

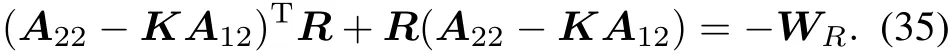
For any σ ∈ (0,1),let cσbe the largest scalar such that

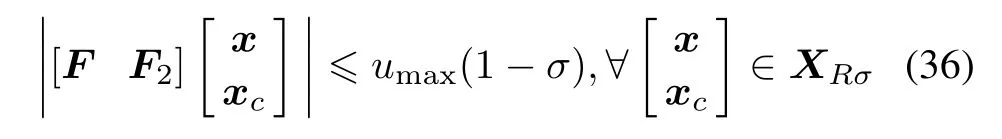
with

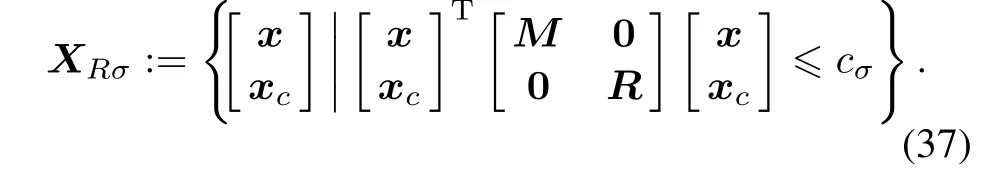
For any non-positive function ρ(y)locally Lipschitz in y,the output feedback control law(33)solves the output regulation problem,if the initial states x0,xc0and v0satisfy the following conditions:

and

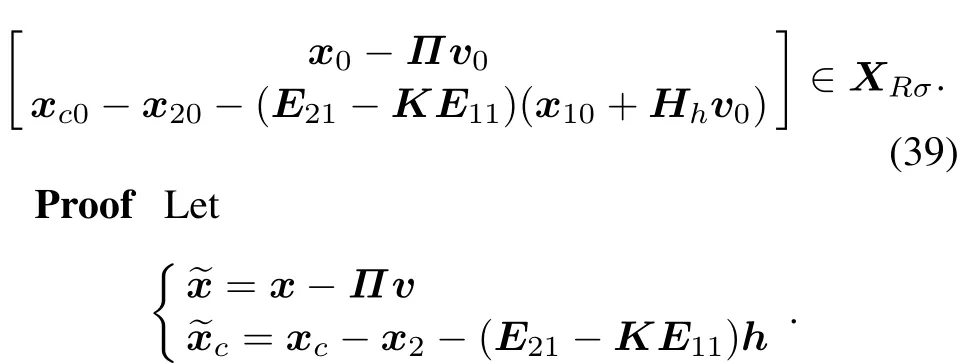
Noting that|Γv|? σumax,we can obtain that

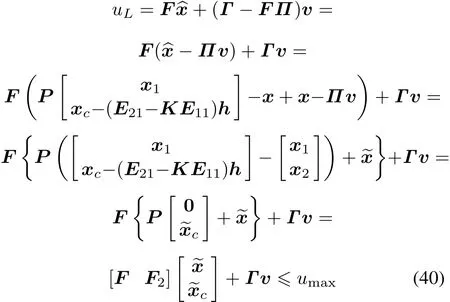
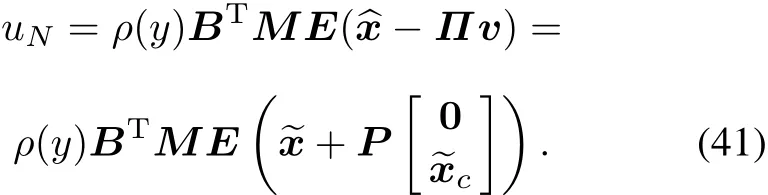
Then the closed-loop system can be written as

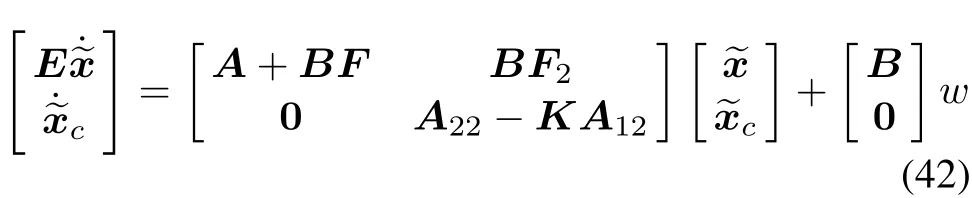
where

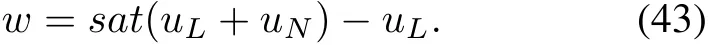
Define a Lyapunov function as follows:

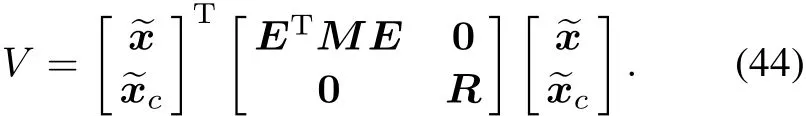
Then

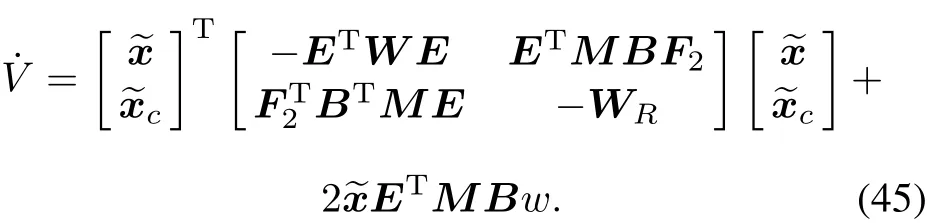
Consider the following cases:

Case 1:If|u|?umax,then w=uN;

Case 2:If u＞umax,then uN＞umax-uL=w＞0;

Case 3:If u＜-umax,then uN＜umax-uL=w＜0.

From above,we can express w as

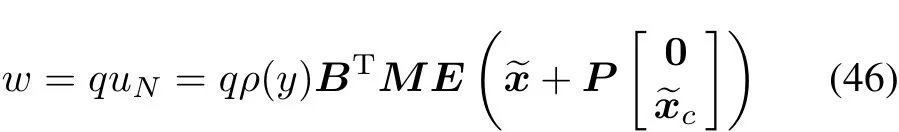
where q(t)∈[0,1]is a piecewise continuous function.Then

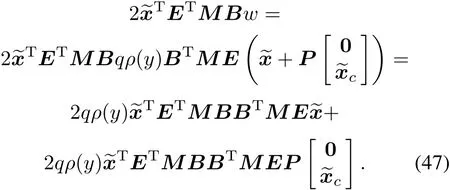
Let

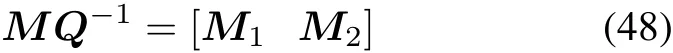
where M1∈ Rn×p,and M2∈ Rn×(n-p),we have

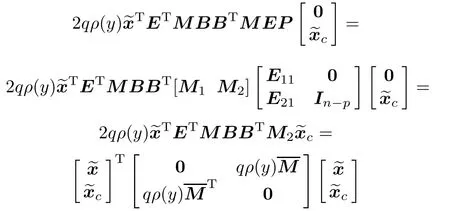
Denoting

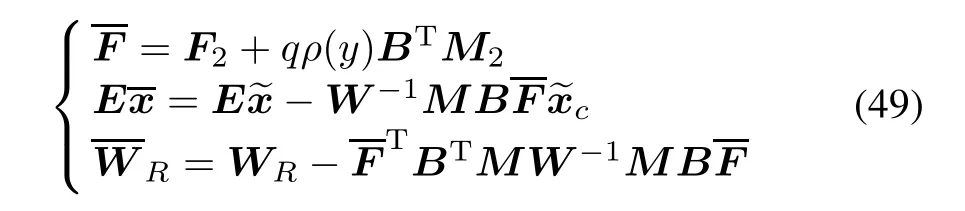
then we have

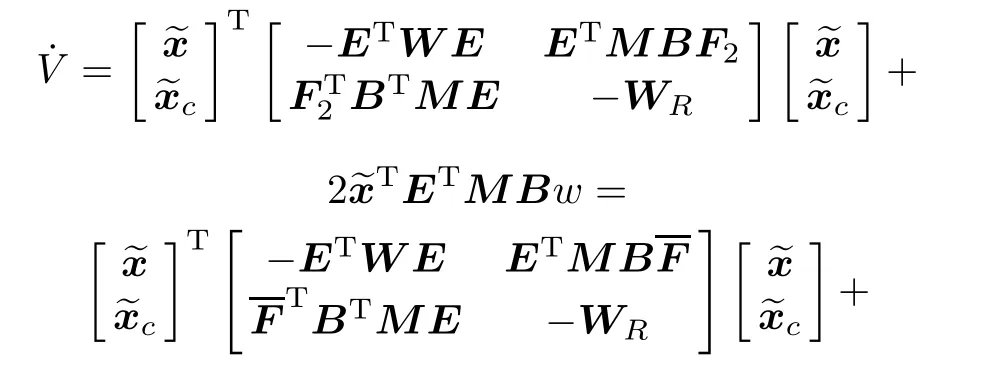
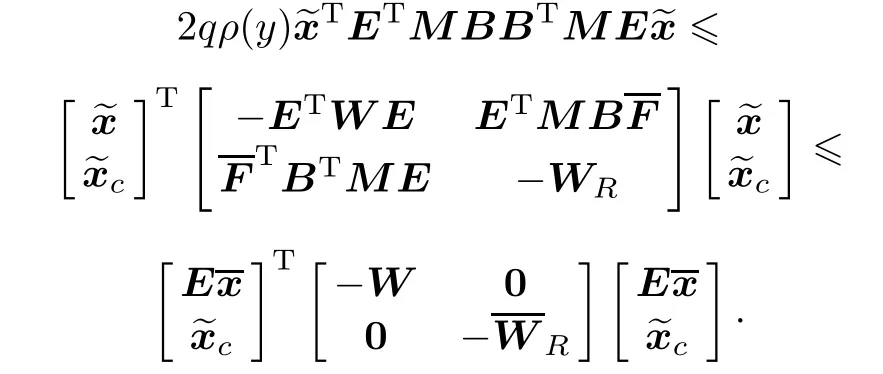
Since WR＞and ρ(y)is locally Lipschitz in y,we can easily know that there exists a ρ?＞ 0 such that for any function satisfying|ρ(y)|? ρ?,we have＞0,hence

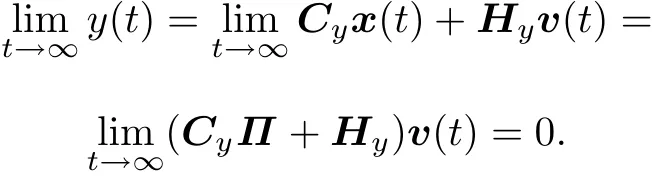
This completes the proof of Theorem 2.

Remark4 Theorem2establishes the solvability conditions of the output regulation problem by output feedback CNF control.Theorem 2 is proved by showing that the closed-loop system under the output feedback CNF control law(33)satisfies Requirement 3 and Requirement 4.Similar to the state feedback case,the solvability conditions described by Theorem 2 covers the results of[26]and[28].Specifically,ifE=I in(1),i.e.,the system is reduced to a normal linear system,Theorem2 is equivalent to Theorem 4.1 of[26].The tracking control problem of singular linear system by the output feedback CNF control problem is not considered in[28],but Theorem 2 can provide a solution to this problem by letting the exo-system

5.An illustrative example

Consider a simple circuit network as shown in Fig.1,where voltage source VS(t)is the driver(control input),R,L,and C stand for the resistor,inductor,and capacity,respectively,as well as their quantities,and their voltages are denoted by VR(t),VL(t),VC(t),respectively.

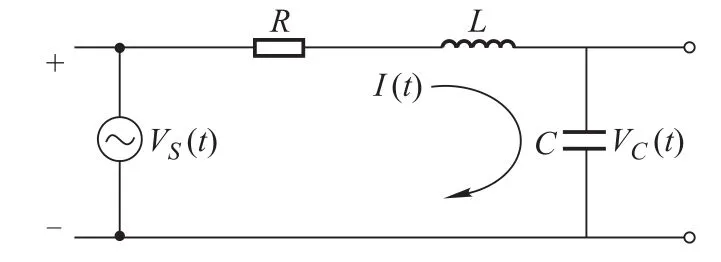
Fig.1 A simple circuit network

Then from Kirchhoff’s laws,we have the following circuit equations[1]:

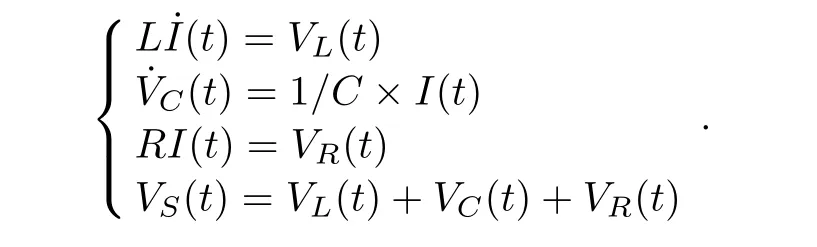
If we choose state variable x(t),control input u(t)and controlled output y(t)as

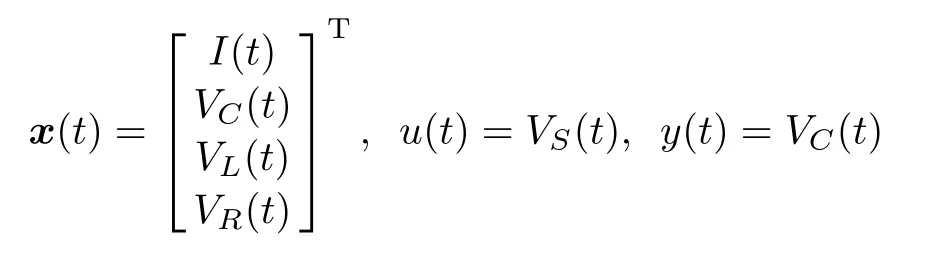
respectively,and assume that the circuit network is disturbed by some sinusoidal signal v(t),the system becomes

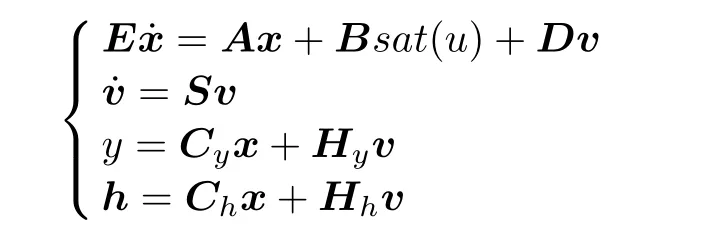
where

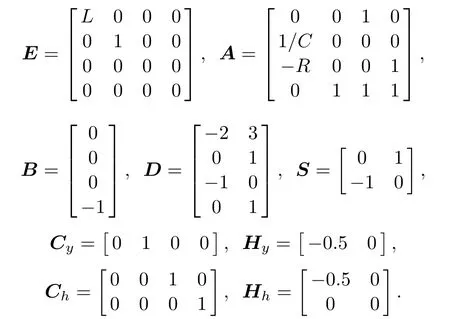
and choose L=1H,C=1F,and R=1Ω for simplification.We assume that the max voltage of VS(t)is 1.4 V.

5.1 State feedback control

We can easily show that the system satisfies Assumptions 1-4.Also,the singular regulator equation(8)has a solution as follows:

Let F=[-2 -4 0 1],then

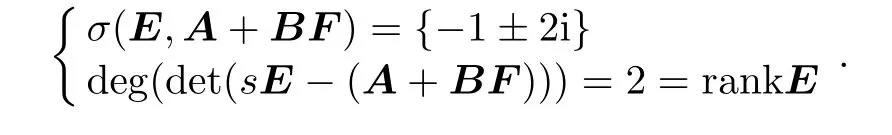
Thus(E,A+BF)is stable and impulse free.Let W=I,we can obtain M from(12)that

As proposed in[6],the nonlinear function ρ(y)can be selected as

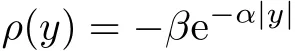
where β =45,α =150.

Assume that the initial states are given by x0=(0,0.2,0,0)T,v0=(0.2,0)T,we can easily know the initial states satisfy(16)and(17).According to the above CNF control law and selected initial conditions,the simulation results are shown in Fig.2 and Fig.3,where the control input and controlled output under state feedback linear control and state feedback CNF control are compared.

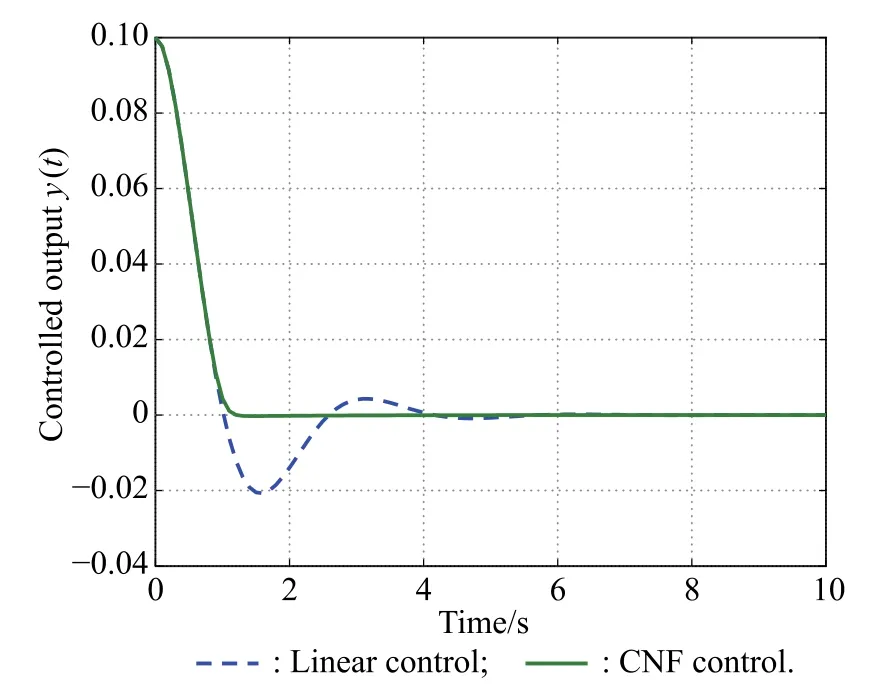
Fig.2 Trajectory of controlled output y(t)by state feedback

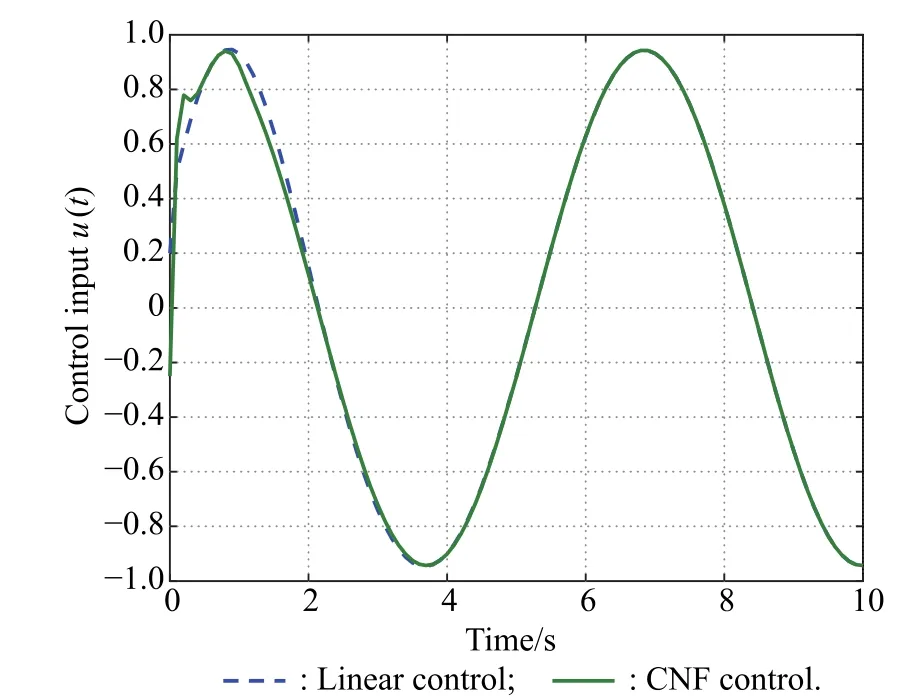
Fig.3 Trajectory of control input u(t)by state feedback

The linear control law is obtained by letting the nonlinear part be zero,i.e.,ρ(y)=0.Under the linear control law,there exists a large overshoot,and the settling time is also large.Under the CNF control law,the overshoot caused by the linear control law is reduced significantly by the nonlinear part of the CNF control law,the output y(t)converges to zero quickly and smoothly without overshoot. Both the linear control law and the CNF control law are not not saturated.

5.2 Output feedback control

In this subsection,we assume that the state x is not measurable.It is easy to verify that the system satisfies Assumptions 1-6.Let

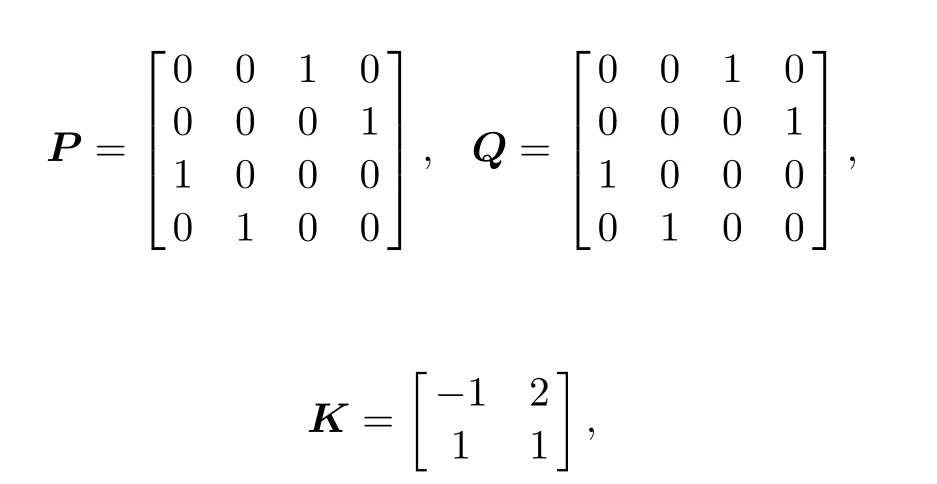
we can obtain

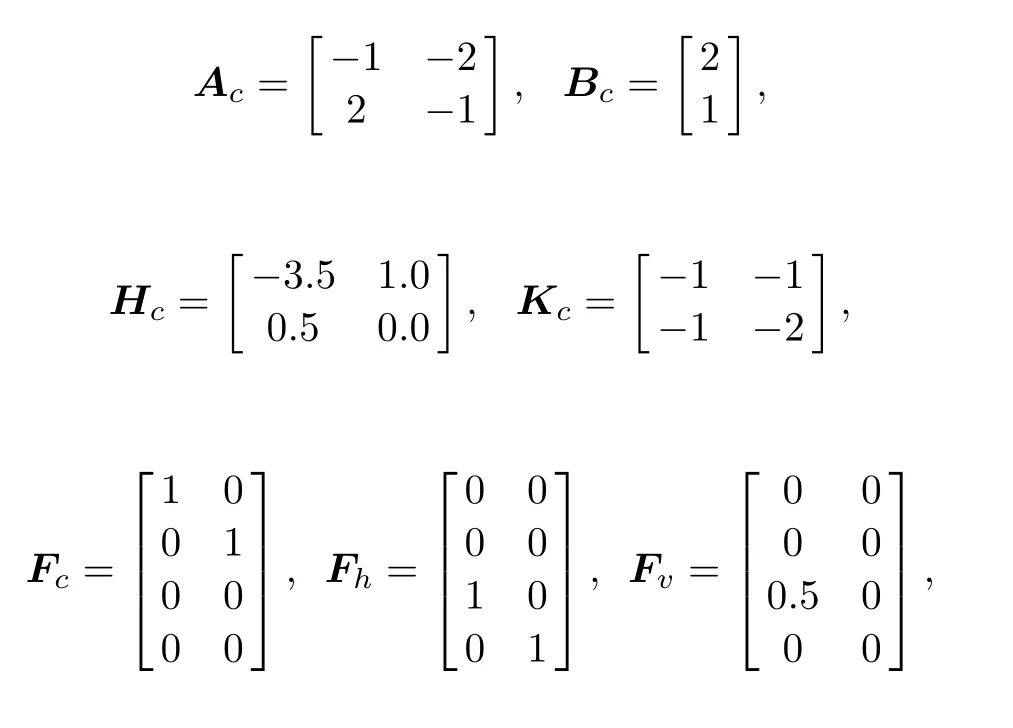
andσ(A22-KA12)={-1±2i}.Thuswe can find a positive definite solution R＞0 for the Lyapunov equation(35).

The initial states of the system are selected as x0=(0,0.2,0,0)T,v0=(0.2,0)T,and xc0=(0.1,0)T.It is easy to show that the initial states satisfy(38)and(39).Using the nonlinear function ρ(y)in the form of(51)with β=230,α=243,the simulation results are shown in Fig.4 and Fig.5.The closed-loop performance under the output feedback control is quite similar to the case under the state feedback control.However,the transient performance is degenerated a little because of the observer for both the linear control law and the CNF control law.

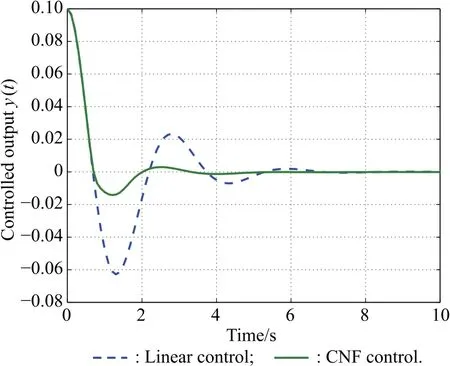
Fig.4 Trajectory of controlled output y(t)by output feedback

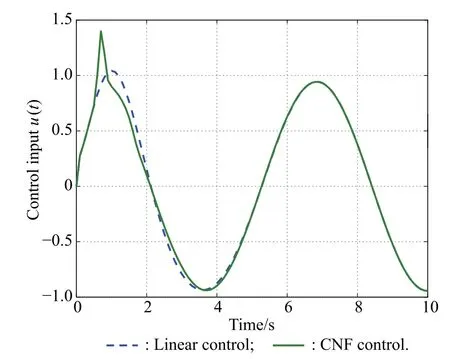
Fig.5 Trajectory of control input u(t)by output feedback

6.Conclusions

The output regulation problems for singular linear systems with input saturation are solved by state feedback composite nonlinear feedback control and output feedback composite nonlinear feedback control respectively.Comparing with the existing methods,the proposed control law can significantly improve the transient performance of the closed-loop system by carefully designing the linear feedback part and the nonlinear feedback part of the composite nonlinear feedback conntrol law.However,it should be noted that only local output regualtion problem is addressed in the paper.It would be interesting if the results of this paper can be extended to semi-global output regulation problem of singular linear systems with input saturation.