張 林,李存林,郭文娟

(1.北方民族大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,寧夏銀川 750021)

(2.北方民族大學(xué)管理學(xué)院,寧夏銀川 750021)

1 引言

隨著社會(huì)經(jīng)濟(jì)的快速發(fā)展,傳染病和流行病給人們的生活、社會(huì)發(fā)展等帶來(lái)了很大的危害.越來(lái)越引起了許多生物數(shù)學(xué)和疾病預(yù)防等工作者的重視,并取得了一些研究成果[1–5].考慮如下經(jīng)典的SIRS傳染病模型[6]:

其中符號(hào)皆為正的常數(shù),意義表示如表1.

表1:符號(hào)及其含義

眾所周知,通過(guò)媒體報(bào)道可以降低人與人之間的接觸率,這在2003年的非典[4,7,8]和2013年的H7N9[9]傳染病中已經(jīng)得到了證實(shí).作為一種新型的傳染病H7N9于2013年首次出現(xiàn)在上海,它和非典一樣,短時(shí)間內(nèi)在人類迅速傳播開(kāi).后來(lái)人們通過(guò)電視的報(bào)道了解到H7N9是通過(guò)人與人之間的接觸傳播的,于是大部分人采取盡量少出門,少參加一些社會(huì)活動(dòng)來(lái)降低人與人之間的接觸率,這確實(shí)在一定程度上減少了疾病的傳播.

然而,模型(1.1)中并沒(méi)有考慮媒體報(bào)道對(duì)傳染病的影響.事實(shí)上,由于媒體報(bào)道的因素,傳染率β是會(huì)減小的[4].因此將傳染率β表示為媒體報(bào)道的函數(shù),即β=β1?β2f(I),那么模型(1.1)轉(zhuǎn)換為

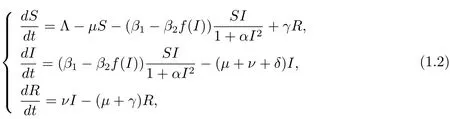
其中β1是不考慮感染者的一般接觸率,β2是因感染者的存在而減少的最大接觸率.因?yàn)槊總€(gè)人與他人的接觸不可避免,故而假設(shè)β1＞β2.函數(shù)f(I)滿足

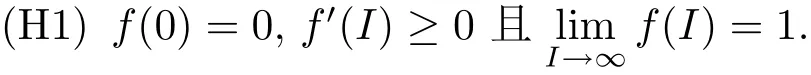
模型(1.2)是在模型(1.1)的基礎(chǔ)上考慮了媒體報(bào)道對(duì)疾病的影響,并且證明了R0=1的情形,即當(dāng)R0=1時(shí),無(wú)病平衡點(diǎn)仍然是全局漸進(jìn)穩(wěn)定的.本文第二節(jié)首先給出了模型(1.2)的基本再生數(shù),并討論了模型(1.2)平衡點(diǎn)的存在性;第三節(jié)在平衡點(diǎn)存在的情況下討論其無(wú)病平衡點(diǎn)和地方病平衡點(diǎn)的全局漸進(jìn)穩(wěn)定性,從而得知疾病的滅絕與持久是由基本再生數(shù)控制的.最后通過(guò)數(shù)值模擬對(duì)得出的結(jié)果進(jìn)行了驗(yàn)證.

2 基本再生數(shù)和平衡點(diǎn)的存在性

首先給出模型(1.2)的一個(gè)控制疾病持久與滅絕的臨界值[10]–基本再生數(shù)[11]

設(shè)Nt=St+It+Rt,將模型(1.2)中的三個(gè)方程相加可得

兩邊同時(shí)對(duì)t積分

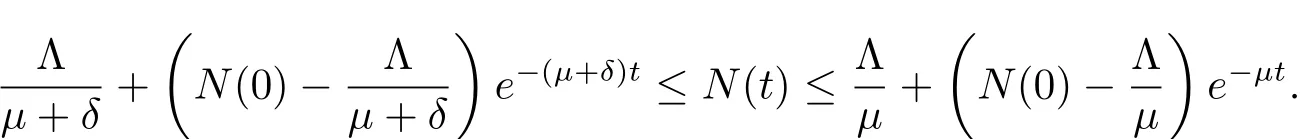
因此

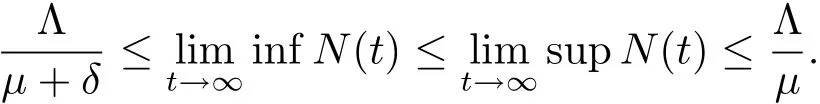
根據(jù)上述推理現(xiàn)在定義一個(gè)有界集Γ:

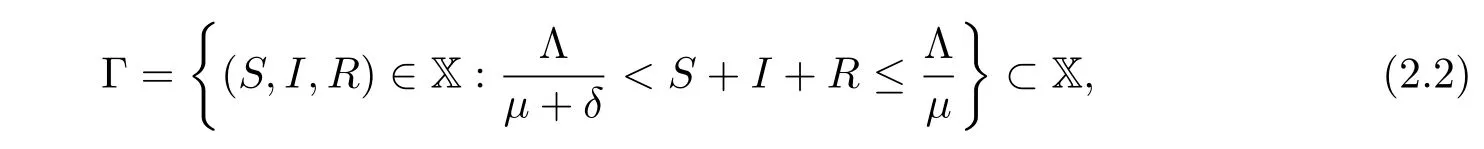
下面繼續(xù)討論地方病平衡點(diǎn) E?=(S?,I?,R?)的存在性.設(shè)E?=(S?,I?,R?)是下列方程組的一個(gè)解

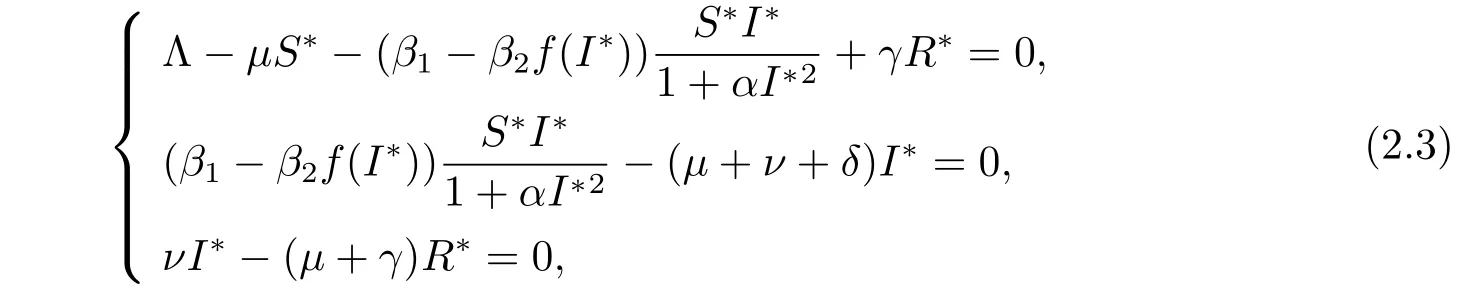
對(duì)方程組(2.3)求解可得

且

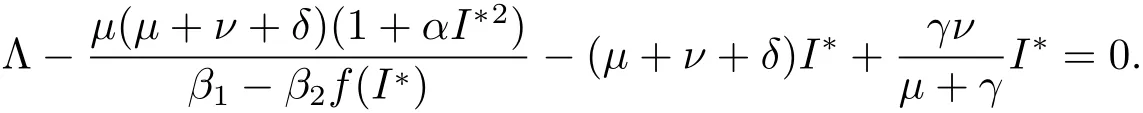
令

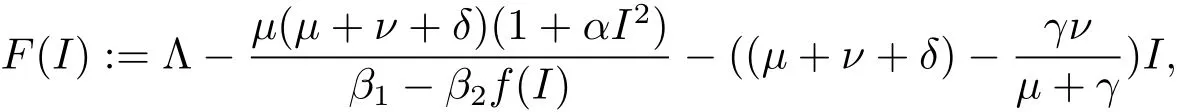
根據(jù)假設(shè)(H1)可知F(I)是一個(gè)減函數(shù),因此

若R0＞1,F(I)=0存在一個(gè)正解I?,則模型(1.2)存在唯一的地方病平衡點(diǎn)E?=(S?,I?,R?),其中

3 平橫點(diǎn)的全局漸進(jìn)穩(wěn)定性

下面討論模型(1.2)的無(wú)病平衡點(diǎn)E0和地方病平衡點(diǎn)E?的全局漸進(jìn)穩(wěn)定性.

定理3.1 若R0≤1,則模型(1.2)的無(wú)病平衡點(diǎn)是全局漸進(jìn)穩(wěn)定的.

證 定義一個(gè)Lyapunov函數(shù)

∈足夠小.則有

令

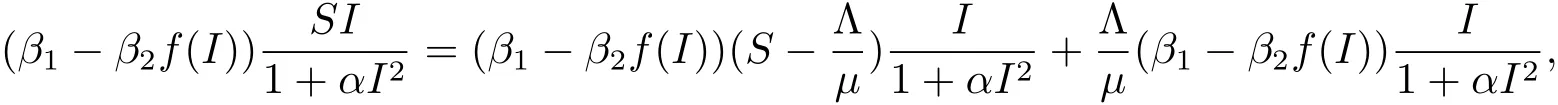
因此

分析 θ1Λ(β1? β2f(I))? μ(1+αI2)(θ1(μ + ν+ δ)? θ2ν),有

將上面的不等式代入(3.2)式,可以得到

(1)當(dāng)R0＜1時(shí),

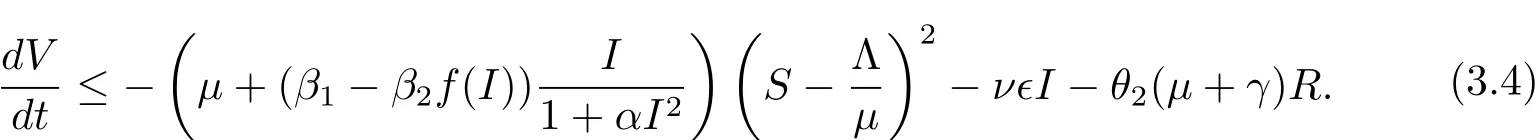
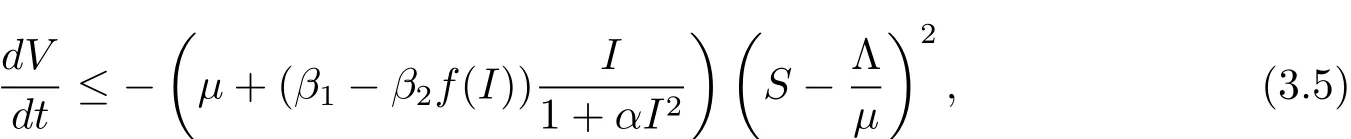
(2)當(dāng)R0=1時(shí),θ2=0,從(3.3)式可以得到當(dāng)且僅當(dāng)根據(jù)LaSalle不變?cè)?模型(1.2)的任意解都收斂到B,其中B?{(S,I,R):,I=0,R=0}是模型(1.2)的最大不變子集,即B={E0}是一個(gè)單點(diǎn)集.因此,當(dāng)R0≤1時(shí),在有界集Γ中,E0是全局漸進(jìn)穩(wěn)定的.證畢.

定理3.2 當(dāng)R0＞1時(shí),模型(1.2)存在唯一的地方病平衡點(diǎn)E?=(S?,I?,R?)是全局漸進(jìn)穩(wěn)定的,且E0是不穩(wěn)定的.

證 將E?代入模型(1.2)的Jacobian矩陣

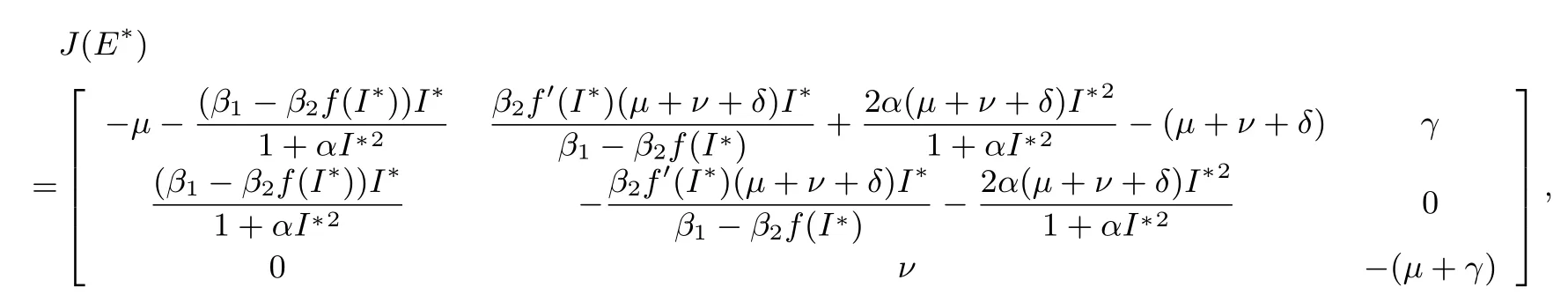
J(E?)的特征多項(xiàng)式為

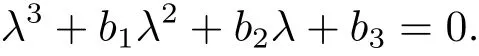
為了計(jì)算b1,b2,b3的值,令

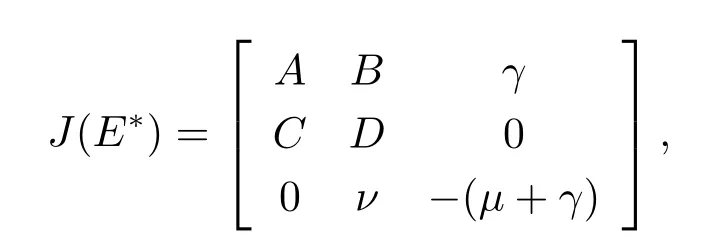
其中

進(jìn)一步計(jì)算可得

因?yàn)?/p>

由于b1＞0,b2＞0且b3＞0,則J(E?)的三個(gè)特征值的實(shí)部都非負(fù),由Routh-Hurwitz準(zhǔn)則可知,E?是局部漸進(jìn)穩(wěn)定的.

令Nt=St+It+Rt,把(1.2)式中的三個(gè)方程相加得則方程(1.2)變?yōu)?/p>

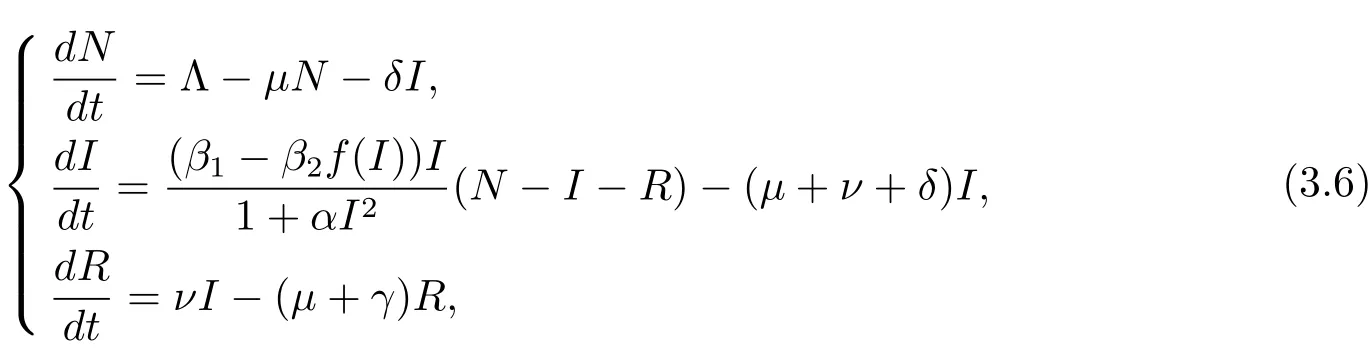
且N?=S?+I?+R?.接下來(lái)繼續(xù)證明模型(1.2)的地方病平衡點(diǎn)E?是全局漸進(jìn)穩(wěn)定的,則只需要證明模型(3.6)的解(N?,I?,R?)是全局漸進(jìn)穩(wěn)定的.考慮下面的Lyapunov函數(shù)

其中k1和k2是正常數(shù).V的倒數(shù)為

根據(jù)LaSalle漸進(jìn)穩(wěn)定定理[12,13],可知模型(1.2)的地方病平衡點(diǎn)E?是全局漸進(jìn)穩(wěn)定的,又

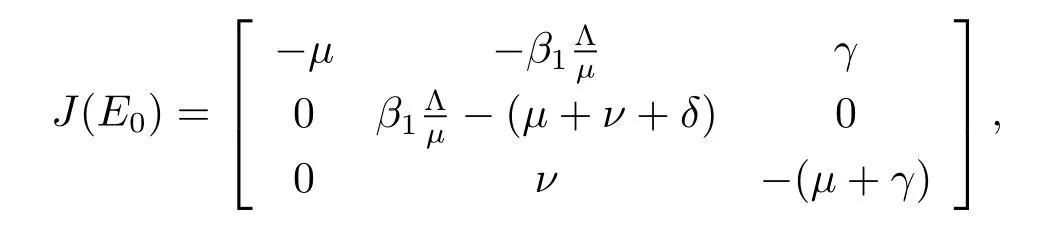
4 數(shù)值分析

下面給出例子對(duì)以上結(jié)論進(jìn)行驗(yàn)證.選取一個(gè)滿足條件(H1)的函數(shù)模型(1.2)可化為

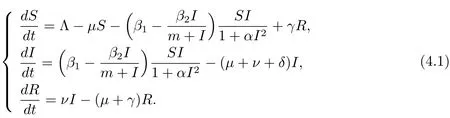
下面對(duì)(4.2)式中的參數(shù)賦值計(jì)算如下表2.

表2:各參數(shù)取值計(jì)算

通過(guò)MATLAB軟件運(yùn)算作圖如圖1.

圖1:對(duì)于三組不同的參數(shù)值,模型(4.1)的解S(t),I(t)和R(t)的時(shí)間序列圖

分析上圖可知在圖1(a)中,因?yàn)镽0＞1,計(jì)算得

選取不同的初值時(shí),S,I,R最后都將趨于唯一的地方病平衡點(diǎn)E?,這說(shuō)明疾病是持久的;在圖1(b)中,因?yàn)镽0=1,計(jì)算得E0=(2.0000,0,0),此時(shí)E?是不存在的,通過(guò)選取不同的初值,S最后都將趨于=2.0000,而I和R逐漸趨于0,即疾病滅絕;在圖1(c)中,因?yàn)镽0=0.5333＜1,計(jì)算得E0=(1.3333,0,0),此時(shí),E?也是不存在的,且選取不同的初值,S最后都將趨于=1.3333,而I和R逐漸趨于0,即疾病滅絕.

綜上所述,無(wú)病平衡點(diǎn)E0=(,0,0)是恒存在的,當(dāng)R0＞1時(shí),存在一個(gè)地方病平衡點(diǎn)E?是全局漸進(jìn)穩(wěn)定的,而當(dāng)R0≤1時(shí),疾病滅絕.

5 結(jié)論

流行病的傳播給人們的生活帶來(lái)了巨大的損失和傷害.因此,本文討論了一類確定性SIRS傳染病模型的持久與滅絕:當(dāng)基本再生數(shù)R0≤1時(shí),疾病是滅絕的;當(dāng)R0＞1時(shí),疾病是持久的.然而在現(xiàn)實(shí)生活中,流行病不可避免地受到隨機(jī)因素的影響,所以下一步將要討論不確定環(huán)境下隨機(jī)擾動(dòng)對(duì)模型(1.2)的影響.