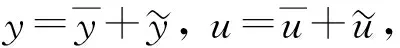杜 潤 梅

(長春工業(yè)大學(xué) 基礎(chǔ)科學(xué)學(xué)院, 長春 130012)

考慮如下耦合系統(tǒng):

其中:QT=Ω×(0,T),Ω是n中的非空有界區(qū)域, 其邊界?Ω分片光滑,T>0;h∈L2(QT);χ是特征函數(shù);ω是Ω中的非空開子集;bj,cj∈L∞(QT),j=1,2;y0,u0∈L2(Ω); 函數(shù)滿足條件a(x,t)>0, (x,t)∈QT,Σ定義為

由于a(x,t)可能在Ω的邊界處為零, 因此方程組(1)-(2)是邊界退化的拋物方程組[1-2]. 目前, 關(guān)于退化拋物方程可控性的研究已有很多結(jié)果: 文獻[3-6]研究了如下退化拋物方程:

其中b,c∈L∞(QT), 在相應(yīng)的初邊值條件下, 證明了該系統(tǒng)的近似可控性; 文獻[7]研究了當(dāng)b1=b2=0時, 耦合系統(tǒng)(1)-(4) 的近似可控性. 本文利用文獻[7]的方法, 通過對共軛系統(tǒng)的研究, 證明問題(1)-(4)的近似可控性. 即證明對任意允許誤差ε>0和任意給定的(yd,ud)∈L2(Ω)×L2(Ω), 存在控制函數(shù)h, 使得問題(1)-(4)的解(y,u)在時刻T處可近似達到(yd,ud), 即

(5)

定義1如果對任意滿足φt,ψt∈L2(QT)和φ(·,T)|Ω=ψ(·,T)|Ω=0的φ,ψ∈C([0,T];L2(Ω))∩B, 有

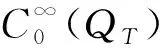
類似文獻[3]中引理2.1, 可以證明系統(tǒng)(1)-(4)的適定性:

定理1系統(tǒng)(1)-(4)存在唯一弱解(y,u), 且滿足

其中C>0是一個僅依賴于Ω,T,‖b1‖L∞(QT),‖b2‖L∞(QT)‖c1‖L∞(QT),‖c2‖L∞(QT)的常數(shù).

考慮系統(tǒng)(1)-(4)的共軛系統(tǒng):

定義映射

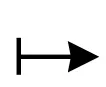
命題1共軛系統(tǒng)(6)-(9)具有唯一延拓性, 即若z在Qω上幾乎處處為0, 則z和v在QT上幾乎處處為0.

證明: 由方程(6)及z在Qω上幾乎處處為0, 可知v在Qω上幾乎處處為 0. 對充分小的δ>0, 記Ωδ={x∈Ω: dist(x,?Ω)>δ}. 在Ωδ×(0,T)上, 方程(6),(7)是非退化的. 由一致拋物方程的唯一延拓性[8]可知,u和v在Ωδ×(0,T)上幾乎處處為 0. 再由δ的任意性可知,u和v在QT上幾乎處處為0. 證畢.

對于(z0,v0)∈L2(Ω)×L2(Ω), 定義泛函

類似文獻[7]中命題2.2, 可得如下結(jié)論.

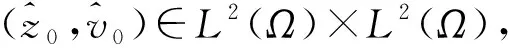
定理2當(dāng)(y0,u0)=(0,0)時, 系統(tǒng)(1)-(4)是近似可控的, 即對任意給定的yd,ud∈L2(Ω)和ε>0, 存在函數(shù)h∈L2(QT), 使得系統(tǒng)(1)-(4)的解(y,u)滿足式(5).

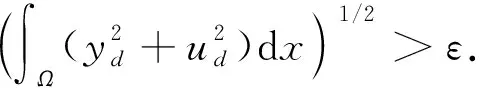
(10)

由(y,u)是系統(tǒng)(1)-(4)的弱解可知,

由(θ,ψ)是系統(tǒng)(6)-(9)當(dāng)(z0,v0)=(θ0,ψ0)時的解可知,

由式(11)-(14), 可得

(15)

由(θ0,ψ0)的任意性可知式(5)成立. 證畢.

定理3對任意的(y0,u0)∈L2(Ω)×L2(Ω), 系統(tǒng)(1)-(4)是近似可控的.

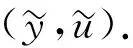
(16)