Mingyue Zhou＊, Xiaohui Zhao

1 College of Computer Science and Engineering, Changchun University of Technology, Changchun 130012, China

2 Key Laboratory of Information Science, College of Communication Engineering, Jilin University, Changchun 130012, China

Abstract: In order to solve the problem that traditional energy efficiency power allocation algorithms usually require the assumption of constant or perfect channel state information in cognitive radio networks (CRNs), which may lead to performance degradation in real systems with disturbances or uncertainties,we propose a robust energy efficiency power allocation algorithm for underlay cognitive radio (CR) systems with channel uncertainty in consideration of interference power threshold constraint and minimum target SINR requirement constraint. The ellipsoid sets are used to describe the channel uncertainty, and a constrained fractional programming for the allocation is transformed to a convex optimization problem by worst-case optimization approach.A simplified version of robust energy efficiency scheme by a substitutional constraint having lower complexity is presented. Simulation results show that our proposed scheme can provide higher energy efficiency compared with capacity maximization algorithm and guarantee the signal to interference plus noise ratio (SINR) requirement of each cognitive user under channel uncertainty.

Keywords: cognitive radio; power allocation;spectrum sharing

I. INTRODUCTION

Cognitive radio as a promising technology has drawn considerable attentions due to its high utilization rate of frequency spectrum. In this paradigm, cognitive users or second users(SUs) are allowed to coexist with primary users (PUs) while assuring that the performance degradation for transmission of PUs is tolerable [1].

Power allocation plays a key role to get higher performance in communications of CR systems. Early works on power allocation focus on capacity maximization algorithm(CMA) subject to interference threshold constraint, e.g, in [2]-[5]. In [2], a power allocation algorithm aims at maximizing the cognitive radio network throughput under interference constraints of PUs. In [3] and [4],the authors study the power allocation strategies to maximize the ergodic capacity and the outage capacity on fading channel of SUs under different types of power constraints and fading channel models. They maximize the ergodic/outage capacity under the average/peak transmit power constraint along with the outage probability constraint of PU. In [5],the authors propose a distributed power con-trol algorithm to maximize the sum cognitive throughput under the constraint of queue stability of PU.

Recently, consideration of energy efficiency is becoming increasingly important in the cognitive radio networks, since energy efficiency system prolongs life of battery and decreases interferences to other users in the network.In [6], the authors propose an optimization framework for energy-efficiency robust power allocation in network location with imperfect knowledge of network parameters. To mitigate the intertier interference and improve energy efficiency performances in heterogeneous cloud radio access networks, characterizing user association with remote radio heads/high-power node is considered in [7], and the traditional soft fractional frequency reuse is enhanced. But these two algorithms do not consider the situation in CRNs. In [8], the authors present a solution for an energy efficiency resource allocation problem which maximizes the cognitive radio link capacity in consideration of availability of subcarriers and limits on total interference generated to PUs.A novel power allocation algorithm named water-filling factors aided search is proposed in [9] to solve energy efficiency optimization problems under the total power constraint,the interference power constraint and the rate constraint. In [10], the authors propose a strategy that adequately adjusts transmit power of SU to increase current transmission probability while respecting a given constraint on achievable primary rate. However, these energy efficiency power allocation strategies usually assume that channel state information is constant or perfect, but the violation of this assumption may lead to performance degradation in practical systems. In fact, both users and spectrum holes can randomly appear all the time in CRNs, which makes the CRNs a highly dynamic and challenging wireless environment [11]. Therefore, finding robust resource allocation strategies is very crucial to optimize energy efficiency performance of cognitive radio networks.

In this paper, we study the energy efficiency power allocation problem in CR systems under the interference power constraint and the SINR requirement constraint. Our aim is to maximize the energy efficiency of the cognitive radio networks while considering channel uncertainties. The main contributions of this paper are summarized as follows:

1) The ellipsoid sets are used to depict channel uncertainties and a robust energy efficiency algorithm (REEA) is proposed to realize power allocation with interference power threshold constraint and the minimum target SINR requirement constraint.

2) Our robust energy efficiency power allocation with infinite constraints, a constrained fractional programming problem, is formulated as a convex optimization problem solved by considering worst-case optimization approach. A simplified version of REEA scheme with lower complexity under a substitutional constraint is also given.

The rest of the paper is organized as follows. In section II, we present the system model. Section III provides the robust energy efficiency problem formulation and formulates our optimal task. In section IV, we propose our distributed power allocation scheme for REEA based cognitive systems. Section V gives the simulation results and discussions for some extended cases. The conclusions are given in section IV.

In this paper, we have investigated the problem of energy efficiency power allocation for underlay CR systems with channel uncertainty catering to the interference power threshold constraint and minimum target SINR requirement constraint.

II. SYSTEM MODEL

We focus on the underlay paradigm for an adhoc cognitive radio network. There is a set of I users in the CRN. Each user contains a transmitter node and a receiver node. We assume that all the links of SUs share same spectrum band with one PU under the constraint that the interference power introduced to the PU below a certain threshold [12], i.e.,

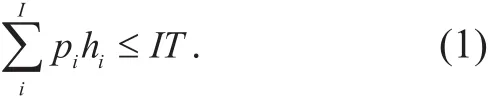
Where p=[p1,p2,…,pI] denotes the vector of the transmit power of the SUs. hiis the channel gain from cognitive transmitter i to the PU receiver. IT represents the permissible interference power threshold that the PU can tolerate.

Let gijbe the channel gain from cognitive transmitter j to cognitive receiver i. The SINR at cognitive receiver i is given by

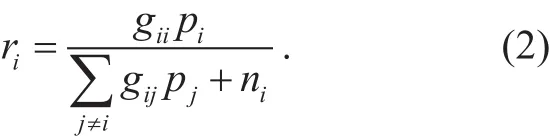
Where niis the background noise of cognitive receiver i. If the SINR at a cognitive receiver drops below the target threshold for relatively long time, the communication between the transmitter and the receiver will fail [13]. In practice, we require

The energy efficiency is defined as the system throughput for unit energy consumption[14], i.e.,

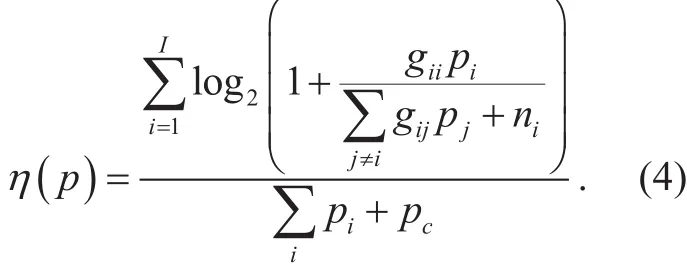
Where pcdenotes the circuit power consumption relatively independent of the transmit power [15].

The energy efficiency power allocation scheme is to maximize the energy efficiency of the CRN while keeping the interference power generated by SUs below a certain threshold and guaranteeing the target SINR requirement.The problem can be formulated as

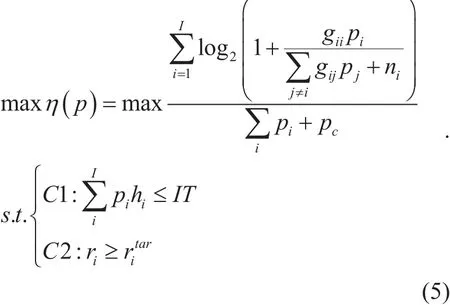
Where 0≤pi≤, andis the maximum budget power of SU i.

In this scheme, each SU optimizes its own energy efficiency performance based on local information, which will reduce the complexity of the CRN. We will refer to the nominal energy efficiency algorithm in (5) as EEA algorithm.

As we know that the CMA scheme is that SU i solves the following optimization problem

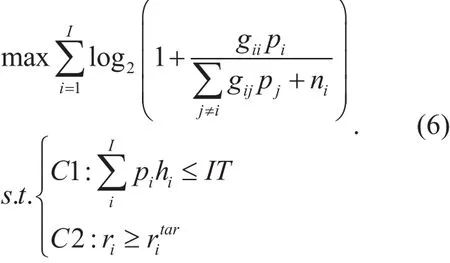
This framework is an eternal pursue of capacity maximization, regardless of transmit power consumption. In addition it only concerns the transmission capacity of the systems but not the problem of its implementation.

III. ROBUST ENERGY EFFICIENCY PROBLEM FORMULATION

In CR systems, PUs and SUs enter or leave the cell in a stochastic manner, which bring channel gain disturbances. The interference power threshold can not be maintained for the EEA scheme (5) if there are the disturbances in hi.Similarly, the SINR requirement for each SU will not be satisfied if gijhas parameter uncertainties.

In this section, we will present a robust energy efficiency algorithm (REEA) for power allocation in the CRN by considering the channel gain uncertainties. In this case, the constraint C2 in problem (5) can be equivalently written as

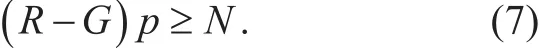
Where R is a diagonal matrix, the elements of this matrix in its main diagonal areandwith

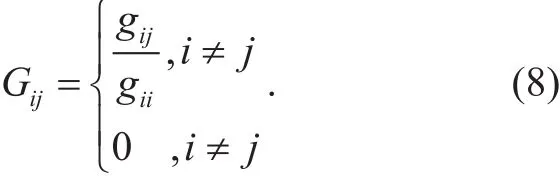
Where G is the normalized channel gains matrix. The formula (7) can get the normalized channel gains with imperfect knowledge.

Let Gijdescribe the fluctuation of channel gains and be decomposed with two components, the nominal termand the perturbation term ΔGijrespectively, i.e.,

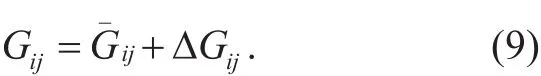
We define Gias a uncertainty set of the ith row in G, and ΔGidenotes the corresponding disturbance. We use ellipsoid approximation to describe Gias

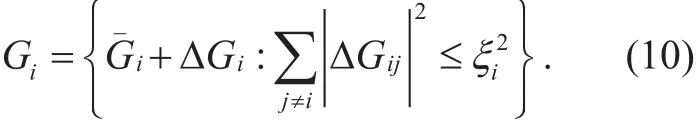
Where ξi≥ 0 is the maximum deviation for ith row in Gi. Accordingly here is no fluctuation for the normalized channel gains when ξi=0, and larger ξiaccounts for larger disturbances.

We denote the channel gain between cognitive transmitter i to cognitive receiver i as, whereand Δgiiare the nominal value and its corresponding perturbation value respectively. The uncertainty in giifor optimization problem (5) is presented as the uncertainty set

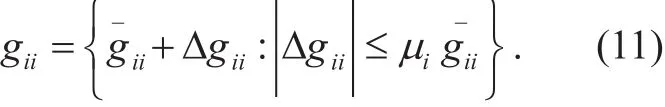
Where μi≥ 0 is a simple percentage to present the upper bound of the perturbation part.

I shall always bear this unforgettable get-together in my mind. With time passing, I believe I will meet many new friends, but I think the friendship among high school classmates will be the purest and will be the most valuable thing to cherish5.

We assume that the channel gains h between SUs to primary transmitter lies in some bounded uncertainty regions. Similarly, we have, whereand Δhidenote the nominal part and the corresponding perturbation part. Therefore, under the condition of the ellipsoid approximation, the uncertain set h can be given by

Where ε≥0 represents the upper bound of deviation for h.

For the consideration of calculation convenience, we substitute the capacity constraint for the SINR requirement constraint in problem (5), or the constraint C2 to the following

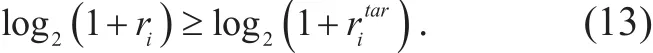
This formula helps us to simplify the design of our power allocation scheme, since it does not introduce new variables. And this constraint also guarantees the SINR requirement for each SU.

The simplified robust version for the energy efficiency power allocation problem considering the channel uncertainty is formulated as follows

Where C3 and C4 constraints in (14) guarantee the interference power threshold and the target SINR requirements will not be violated for any perturbation.

The following representations are obtained by taking account of Cauchy-Schwartz in-equality and the upper bound on the Euclidian 2-norm

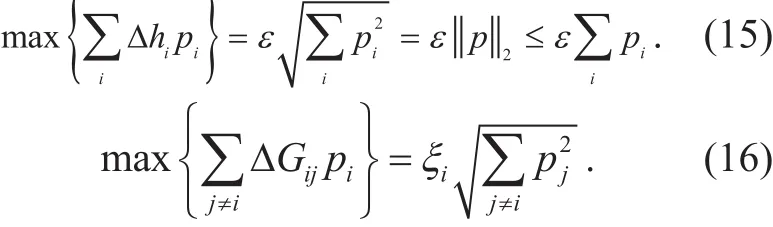
When the worst case scenario is applied to the channel gains {gii}, we have

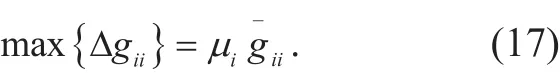
Combining (15)-(17), the optimization problem (14) can be formulated as a deterministic optimization problem

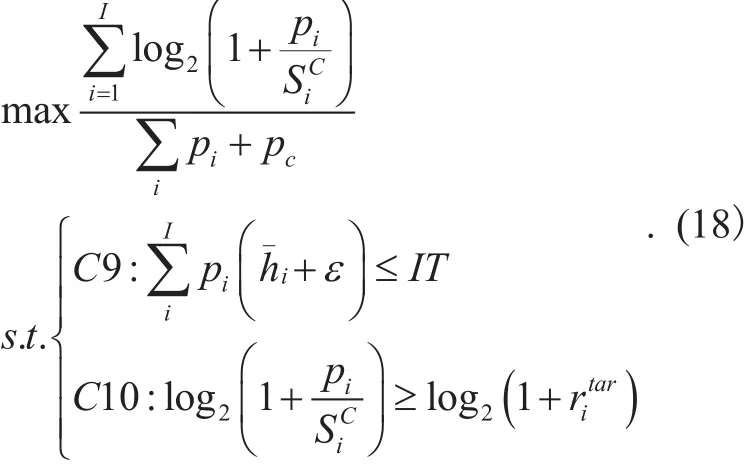
It should notice that this scheme is a conservative algorithm, since real life situations are not always in the worst behavior. However the robust algorithm can guarantee that all SUs continue to demonstrate acceptable performance when there are disturbances in the network [17].

Considering the channel uncertainty, the robust CMA (RCMA) is

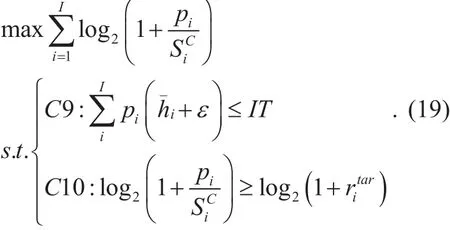
The scheme (19) is a robust strategy, which goes after capacity maximization under the channel uncertainties.

IV. DISTRIBUTE POWER ALLOCATION FOR REEA

Since the problem in (18) is not convex, we rewrite it in a minimization form as

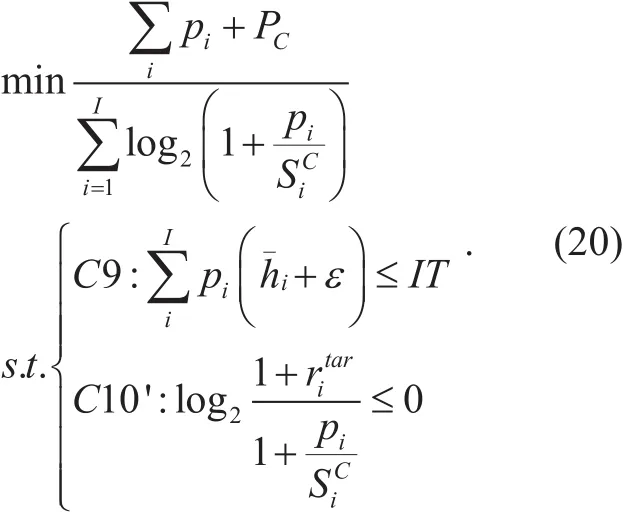
Eq. (20) defines a non-linear constrained fractional programming problem that is difficult to get the optimal solution [18][19]. We also can write a simple fractional optimization problem as

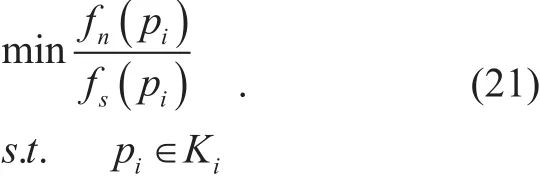
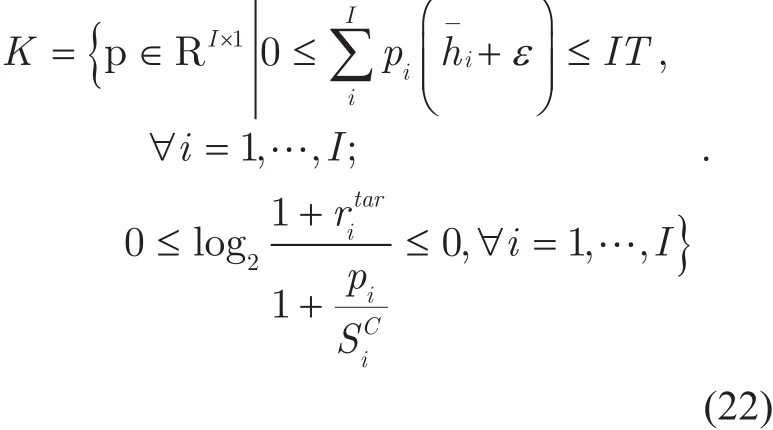
Where Kiis a closed convex subset of K.is a Nash equilibrium of the optimization (21).

The parameter of the objective function is defined as fn(pi)?αfs(pi). Equivalent parametric problem [20] associated with (21) is then

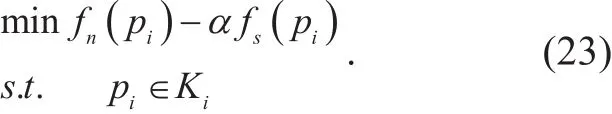
Therefore, the optimization problem in (21) is transformed into a convex optimization problem as (23). We define the optimal value and the solution of (23) asrespectively. According to [21], the optimal solution p*achieves the optimal value α*, if and only if

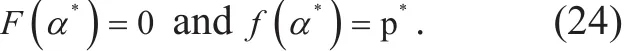
For α*, the power variable of the minimum of fn(pi)?α*fs(pi) is found. The algorithm execution stops if F(α*) is zero or less than an arbitrary small positive value.

For a given α, the Lagrangian of the problem (23) is

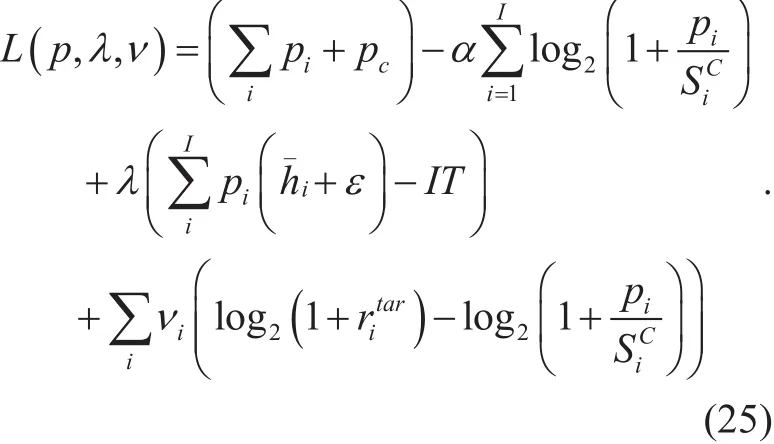
Where λ and νiare the Lagrange multipliers.By the Karush-Kuhn-Tucker [22] condition,the optimal transmit power allocation for each SU can be calculated by

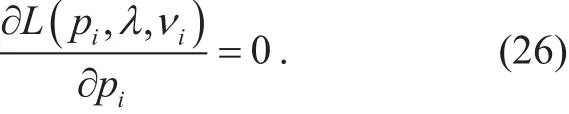
Then the optimal power allocation of SU i is

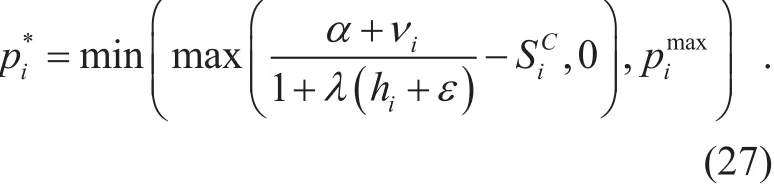
The Lagrange multipliers are

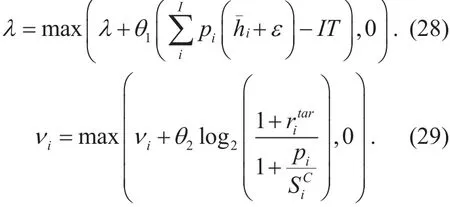
Where θ1and θ2are the iteration step-size.

Each SU gets the optimal transmit power with its REEA which finally reaches an equilibrium point. This strategy provides seamless communication even under the worst situations. In particular, REEA becomes EEA scheme when=0,=0,ε2=0.

V. SIMULATION RESULTS

The performance of our proposed power allocation scheme is presented by numerical experiments. We consider a multiuser cognitive system where there are 3 SUs (I=3)and one PU (M=1) in the region of interest.The interference for channel gains gij,hi, and the background noise niare chosen randomly from the intervals (0.04,0.20), (0.10,0.20) and(0.01,0.10), respectively. And giiare chosen in the interval (0.90,1.00). The permissible interference power threshold is IT=0.2mW and the target SINR at each cognitive receiver is=7.96dB . The circuit power consumption is PC=0.8mW.

For cognitive radio systems, perturbations to channel gains would cause deteriorated system performance. The transmit power of each SU for REEA algorithm with parameter variations is shown in figure 2. Larger parameters mean higher channel disturbance. Larger, ε2, and μiprovide more protection for active SUs at the price of higher power consumption. This shows that each SU requires higher transmit power to compensate for the impact of the channel uncertainty.

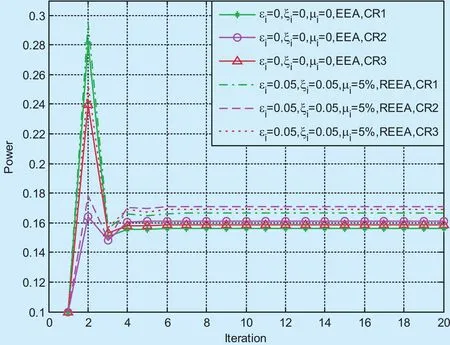
Fig. 1. Transmit power allocation for REEA and EEA.

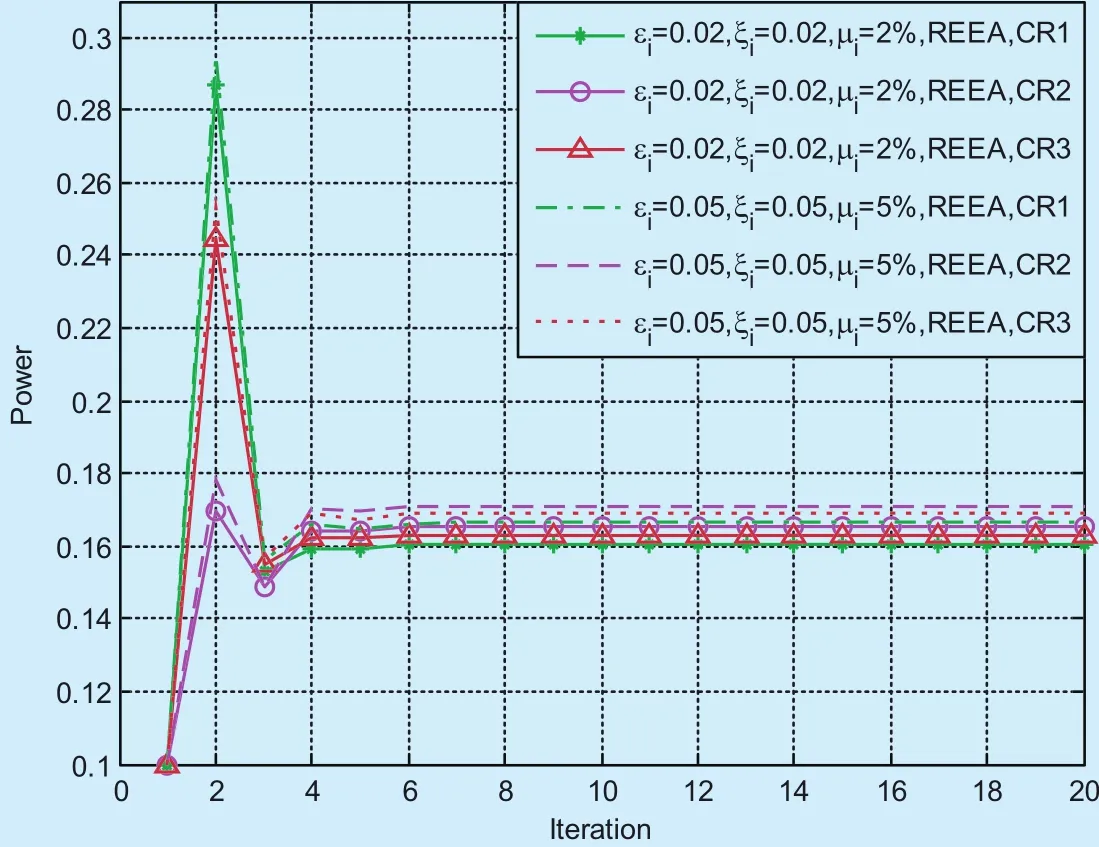
Fig. 2. Power allocation for REEA with parameter variations.

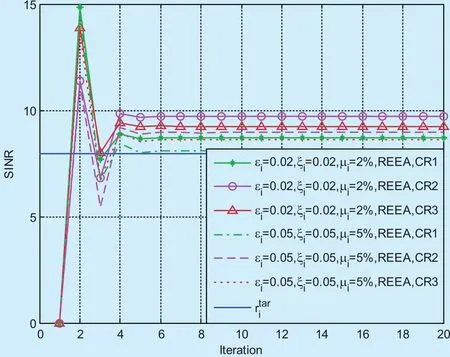
Fig. 3. SINR for REEA with parameter variations.

Fig.3 presents the SINR of each SU for REEA algorithm. The solid line depicts the target SINR requirement for SUs. With the increased of, ε2, and μi, the SINR of the corresponding user decreases, but this SINR with different parameters exceeds the target requirements. Thus REEA scheme can satisfy the SINR requirements with different parameters.

Fig.4 shows the total transmit power under different performance metrics by comparing it with various power allocation algorithms. In figure 4, we find that CMA and RCMA algorithms consume the most transmit power compared with REEA and EEA schemes, since CMA and RCMA pursue capacity maximization. It can be observed that EEA algorithm has least power consumption and the total transmit power for REEA scheme is slightly more than that of EEA scheme. As the disturbances increase, the power allocated to each SU for REEA algorithm increases. Therefore,REEA scheme consumes less total transmit power to get higher energy efficiency.

The energy efficiency of the proposed algorithm and other algorithms are shown in figure 5. EEA scheme has the highest energy efficiency if there are no disturbances in channel gains, which is impossible in practical systems. REEA schemes have the higher energy efficiency compared with RCMA. This efficiency decreases as the channel disturbances increase since more transmit power will be consumed in order to overcome the channel uncertainties. From figure 5, we can conclude that REEA scheme can always maintain higher energy efficiency even with channel gain disturbances.

VI. CONCLUSIONS

In this paper, we have investigated the problem of energy efficiency power allocation for underlay CR systems with channel uncertainty by considering the interference power threshold constraint and minimum target SINR requirement constraint. This problem can be transformed into a max-min problem with the solution of our proposed robust energy efficiency power allocation algorithm. Simulation results indicate that the proposed algorithm can significantly improve energy efficiency of the CR systems

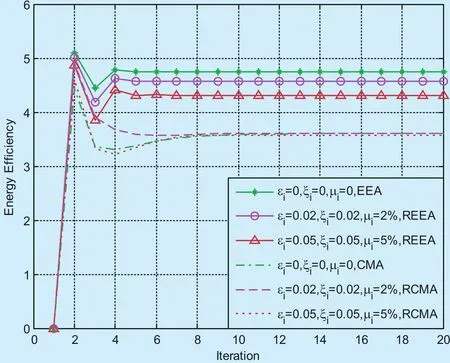
Fig. 5. Energy Efficiency in different metrics.

ACKNOWLEDGEMENTS

This work was supported by the Nation Natural Science Foundation of China (Grant NO.61501059) and the Education Department of Jilin Province (Grant NO. 2016343). The authors would like to thank the editors and the anonymous reviewers for their detailed constructive comments that helped to improve the presentation of this paper.