A Precise Information Extraction Algorithm for Lane Lines
Jinyan Chen, Yaduan Ruan*, Qimei Chen
School of Electronic Science and Engineering, Nanjing University, Nanjing 210023, China
Abstract: Lane line detection is a fundamental step in applications like autonomous driving and intelligent traffic monitoring. Emerging applications today have higher requirements for accurate lane detection. In this paper,we present a precise information extraction algorithm for lane lines. Specifically, with Gaussian Mixture Model (GMM), we solved the issue of lane line occlusion in multi-lane scenes. Then, Progressive Probabilistic Hough Transform (PPHT) was used for line segments detection. After K-Means clustering for line segments classification, we solved the problem of extracting precise information that includes left and right edges as well as endpoints of each lane line based on geometric characteristics. Finally, we fitted these solid and dashed lane lines respectively. Experimental results indicate that the proposed method performs better than the other methods in both single-lane and multi-lane scenarios.
Keywords: multi-lane scenes; lane line occlusion; left and right edges; endpoints of lane lines
I. INTRODUCTION
Lane line detection has two main applications:autonomous driving and intelligent traffic monitoring. For the first application, we mainly use lane line detection to predict the correct driving lane, issue a lane departure warning when the vehicle deviates and finally make adjustments so that the vehicle can drive in the safe area. For the latter one, lane line detection is used to determine whether a vehicle violates traffic rules, like crossing a lane that not allowed, speeding and whether or not the vehicle’s length and width are suitable for driving in the current lane. Besides, this application also needs to judge the congestion level of the current road section by calculating the traffic flow.
The scene of autonomous driving with clear lanes and without shelter is relatively simple.In this scenario, the precise of lane line detection is relatively low but it is enough for roughly predicting the location of correct lane.However, the scene of intelligent traffic monitoring is more complicated. It includes multilane obscured by vehicles easily. Therefore,we need additional pre-processing to obtain clear lane lines compared with autonomous driving scenarios. In addition, in order to realize the above-mentioned functions required by intelligent traffic monitoring, we have to extract more precise information of lane lines like the four endpoints of dashed lane lines instead of roughly locating them.
So far, people have proposed numerous methods for lane line detection. Most of them aim at driving lane prediction, which requires relatively low precise, in autonomous driving scenarios. However, there are few researches focusing on complicated multi-lane detection that needs high precise information of intelligent traffic monitoring scenes.
In this paper, we present a precise information extraction algorithm for lane lines. Fig.1 shows the flowchart of the proposed algorithm.Due to the complexity of the lane environment in traffic surveillance videos, we adopt GMM 0 to generate vehicle-free image, solving the lane occlusion. Then we use the Canny Edge Detector to detect the edges of the default ROI region, where the line segments are detected by PPHT 0. As the number of lane lines in a multi-lane scene is generally more than or equal to three, we use an efficient K-Means clustering 0 for line segments classification rather than simply dividing the left and right.For obtaining precise information about lane lines, we extract the left and right edges as well as the endpoints of each lane line based on its geometric feature. Experiments on single-lane as well as multi-lane scenarios verify the effectiveness of the proposed algorithm.
The rest of the paper is organised as follows. In section II, we introduce the background of lane line detection briefly. Then,section III describes the details of the proposed detection algorithm. Finally, we offer the experiment results including comparison with other methods and conclusions in section IV and V respectively.
We have proposed a method to solve the occlusion of lane lines in traffic surveillance scenes, left and right edges extraction as well as endpoints extraction of lane lines.
II. BACKGROUND
In this section, we will briefly introduce several existing studies of lane line detection. The existing methods include two main research directions, namely, autonomous driving and intelligent traffic monitoring.
Lane line detection algorithms for autonomous driving scenes are as follows: Method[4] presents a robust approach to lane marker detection by generating a top view of the road,filtering with Gaussian kernels and fitting with Random Sample Consensus (RANSAC) [5].Threshold segmentation based algorithm is proposed in document [6], which combines the threshold algorithm, the flood fill as well as Line Segment Detector (LSD) [7] algorithm,to recognize lane lines. Literature [8] introduces a method for road lane detection that distinguishes between dashed and solid lanes based on LSD. Extraction of lane markings using orientation and vanishing point constraints is introduced in Paper [9], which also exploits the line segments extracted by LSD as feature for lane line detecting. Method [10] proposes a novel algorithm to detect varying lane lines like curvy, straight and dashed lane markers.In paper [11], a lane detection algorithm based on dynamic programming is presented. This method can detect lanes with vanishing point estimation. Method [12] gives out the detection method using binary blob analysis along with Hough Transform and Inverse Perspective Mapping (IPM) [13] for lane keeping. In literature [14], an approach for the perception of lanes is introduced, which accumulates and fuses the lane information based on GraphSLAM [15].
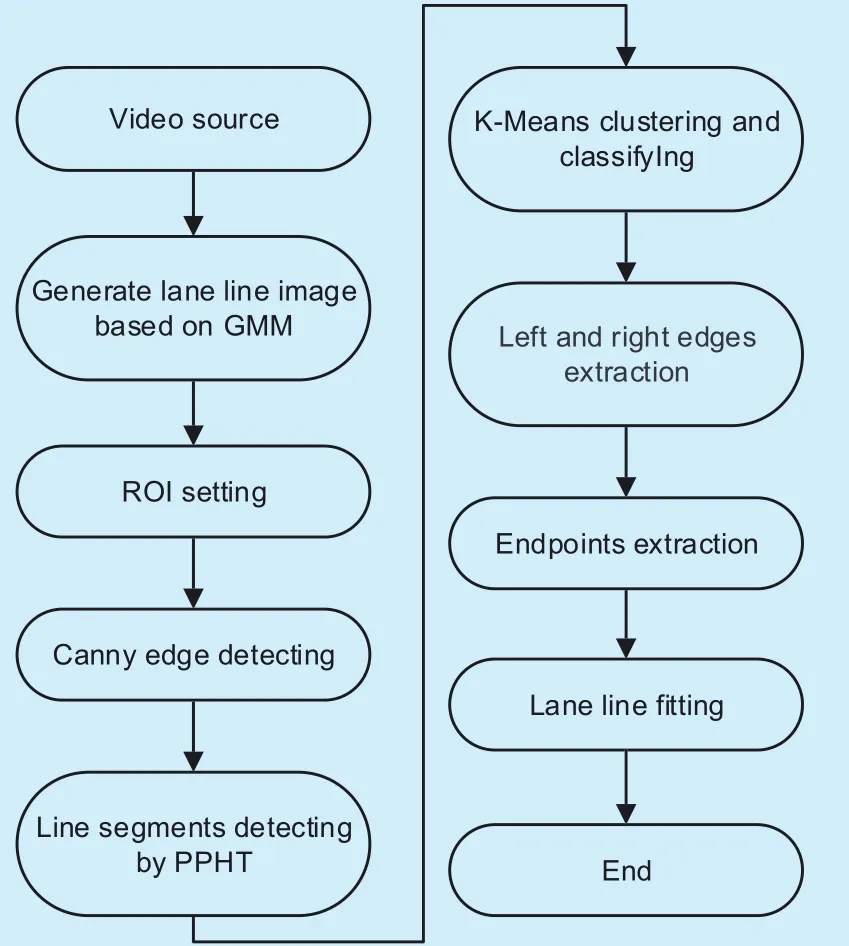
Fig. 1. The flowchart of the proposed algorithm.
There are relatively few lane line detection algorithms for intelligent traffic monitoring scenarios: Approach [16] is one of these few detection algorithms. It detects the proper lane markers by Hough Transform and geometrical restriction. Paper [17] also proposes a lane line detection approach based on Hough Transform as well as Optical Flow, etc. It aims at detecting lanes roughly and identifying vehicles that have departed from their lanes. The detection effects of this method are similar to those of approach [16]. In method [18], a visual surveillance trajectory clustering framework is developed, which extracts the trajectories that are then clustered as candidate lanes and identifies the correct lanes from these candidate lanes in intelligent traffic monitoring scenarios.
III. THE PROPOSED ALGORITHM
In this section, we will give the details of the proposed precise information extraction algorithm, which performs well in both single-lane and multi-lane scenes.
3.1 Extract lane images by GMM

Fig. 2. The lane occlusion image and recovering lane line image.
To generate the vehicle-free image, we use the Gaussian mixture model in this phase for background modelling. Generally, it uses M models that obey the Gaussian distribution to feature each pixel, i.e., each pixel owns a combination of M Gaussian models. Generally, the range of M is 3 to 5. The probability function p(xt) is defined as follows:
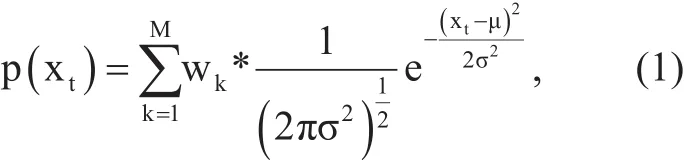
Where xtdenotes the pixel obtained in time t, wkmeans the weight of k-th Gaussian model and k∈[1, M]. Characterμand σ2are the mean and variance of k-th Gaussian model respectively. When M models are initialized, we then pick the former B states to model the lane background:
Once the sum from w1to wkBis greater than the threshold λ, then the kBmodel is selected as one of components for background modelling. Through GMM, we can obtain a satisfying lane line image without occlusion. The following figure 2 (a) shows the lane occlusion image and figure 2 (b) shows the recovering lane line image.
3.2 Lane line detection and classification
After getting the vehicle-free lane image, we adopt the Canny Edge Detector to detect the edges in the default ROI region. Then, we apply PPHT for line segments detecting. When we obtain a complete set of line segments,clustering is required to classify these segments. Therefore, we use a simple and effective K-Means clustering method.
3.2.1 Detecting line segments by PPHT
PPHT is an improvement algorithm of the Standard Hough Transform (SHT). The algorithm has low complexity, and its time performance is better than SHT. Therefore, we use PPHT to detect line segments. Generally, we implement the PPHT method by steps given below:
1) Input a lane image.
2) Select a pixel randomly from the given image to vote for the accumulator and then,remove that point.
3) Get the peak value of the accumulator,and judge whether it is higher than a pre-set threshold T. If the value is less than T, return to step 1).
4) Select the line segment of the longest in the line segments’ set.
5) Delete all the pixels that belong to the above chosen line segment from the input image.
6) Get rid of all the pixels picked in selected line segments from the accumulator in step 3).
7) Output the line segment (i.e. the starting point and the ending point of the line segment)if its length is longer than the minimum value we defined previously.
8) Go back to step 1).
3.2.2 Classify line segments based on K-Means clustering
K-Means with distance as the evaluation index is a typical clustering algorithm. That is, the closer the distance between the two objects,the greater their similarity. Compared with other algorithms, K-means clustering is relatively simple, but also effective. Let X={x1,x2,……, xn} indicates the input data. After K-Means clustering, the output is a set of K clusters. The detailed process is as follows:
1) Select K input data points as initial central values of K clusters.
2) Traverse all the data points and divide them into the nearest cluster based on distance.
3) Calculate the average of each cluster and then apply it to substitute for the original central value of every cluster.
4) Go to step 2) and 3) until it converges or the number of iterations meets our pre-defined value.
In this part, we cluster the line segments captured by PPHT based on K-Means clustering algorithm. First, we change the description of the line segment. The original description of a line segment by PPHT includes the starting point (sx, sy) and the ending point (ex, ey).We need to transform it into the new form:
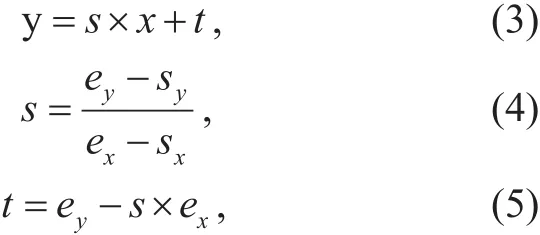
Where s means the slope of a line segment and t represents its intercept. We get all (s, t) pairs as input data points for K-Means clustering.Fig.3 shows the result of line segments classification based on K-Means clustering.
3.3 Left and right edges extraction
Typically, the lane line includes symmetrical left and right edges. This geometric feature can help us extract accurate lane lines, thus providing valuable lane information for other applications. However, many methods ignore this feature. This paper will give full attention to the above characteristic.

Fig. 3. Lane line classification based on K-Means clustering.
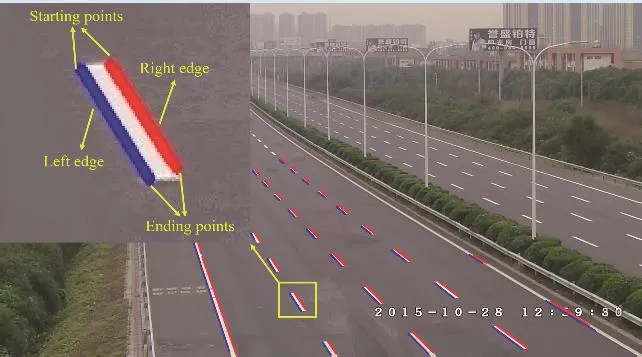
Fig. 4. Left and right edges as well as endpoints extraction.

Fig. 5. Comparison lane line detection results of three methods on Caltech lane data sets. From left to right are method 0, 0 and the proposed method.
After obtaining the classification results of line segments in section 3.2.2, we take the left and right edges of each lane. In view of the geometric characteristic of the lane line, our approach is as follows: for any two different line segments, we calculate the distance between the starting points (ending points) and compare it to the pre-defined threshold. If the distance is less than the threshold, the two input line segments should belong to the same lane line. Furthermore, if the X pixel coordinate of the starting point in a line segment is smaller than the other one. This means that the former is the left edge of the lane line, and the latter is the right one. The detailed pseudo-code is as algorithm 1.
After the left and right edges extraction step, we can easily obtain the four endpoints of each lane line, especially the dashed one.Fig.4 shows the left and right edges as well as the endpoints extraction of the lane line, where the blue mark indicates the left edge and the red one represents the right edge of the lane line. Finally, we fit these solid lane lines and dashed lane lines respectively. For the solid lane line, we adopt the least squares fitting and for the dashed lane line, we use the extracted four endpoints to fit them. Section IV will give the final detection results in both single-lane and multi-lane scenarios.
IV. EXPERIMENTAL RESULTS
In this section, we first provide the comparison of lane line detection results between the proposed method and the other two algorithms(paper 0 and 0) in single-lane scenarios. Then we give out the comparison of detection results between our method and the method [17]in multi-lane scenes. Further, in order to verify the accuracy of the information extracted by our method, we carried out the automatic calibration experiments based on the extracted endpoints. We implemented these experiments on Visual Studio2013 and OpenCV2.4.10 platform.
Since the lane lines in single-lane scenes will not be blocked generally, we omitted the GMM step in these scenes. In addition, whatever it is a single-lane or multi-lane scene, the focus of our attention is always the lower half of the image, i.e., the nearest lane line part.
As shown in figure 5, we provide the comparison results of lane line detection between the above three methods: method 0, 0 and the proposed method, in single-lane scenes provided by Caltech lane data sets 0. The red dashed box in the figure is the lane line part that we concern. From figure 5, it is obvious that our method performs better than method 0 and 0. We can detect those blurry lane lines that are not detected by the other two methods. In addition, we extracted the left and right edges of the lane line and fitted them with vanishing point estimation.
Fig.6 shows the final comparison results of lane line detection between our method and paper [17] in four traffic surveillance multilane scenes. In figure 6, for solid lane lines, we fit them by the least squares method and for dashed ones, we extract the four endpoints of them to fit them. Likewise, the red dashed box is the lane line part that we concern.

Fig. 6. Final comparison of detection results between ours and the method [17] in four multi-lane scenarios. The lower half of each lane line image is our focus.
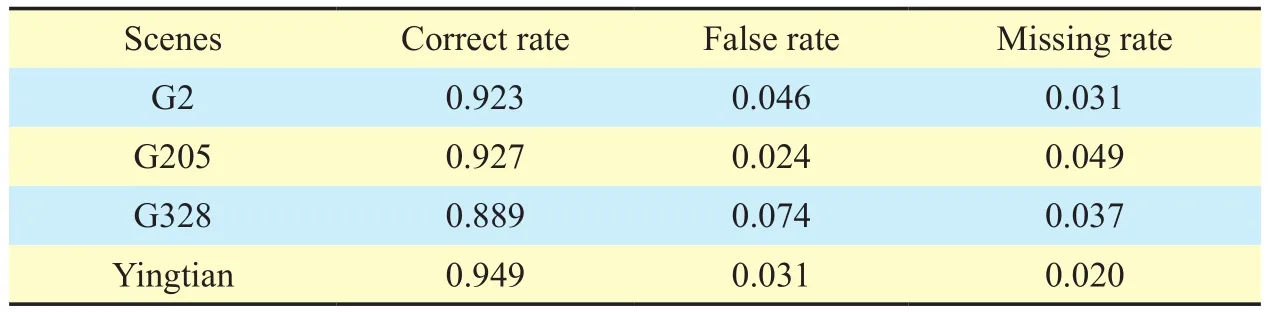
Table I. Detection rates of traffic surveillance multi-lane scenes.
Table 1 shows the detection rates of traffic surveillance multi-lane scenes where the average correct rate is 92.20% with the mean false rate of 4.37% and the mean missing rate of 3.43%. Since the Method [17] didn’t detect the precise information of lane lines, its detection rates were not counted.
Obviously, the method [17] just detects the rough lane lines, so it can only be used for judging whether a vehicle crosses a lane that not allowed. While the proposed algorithm can accurately extract the left and right edges as well as the endpoints of lane lines, which can be used to get the length, width, speed of certain vehicle and the traffic flow, making the intelligent traffic monitoring not only achieve the basic function of method [17], but also access more precise traffic information.
The points of four multi-lane scenes needed in our calibration experiments [19] is shown in figure 7. Table 2, 3, 4 and 5 list the world coordinates of the points in figure 7, where x and y are pixel coordinates in image, X and Y are world coordinates. Table 6, 7, 8 and 9 give the distances of different intervals in tables 2, 3, 4,and 5, respectively. The second line is the reference distance for each interval, the third line is the interval distance we calculated and the fourth line gives the absolute error between the former two terms. We also draw these absolute errors in figure 8 for the sake of intuition. Meanwhile, we adopt the formula (6) to calculate the standard errorσof each multi-lane scene:
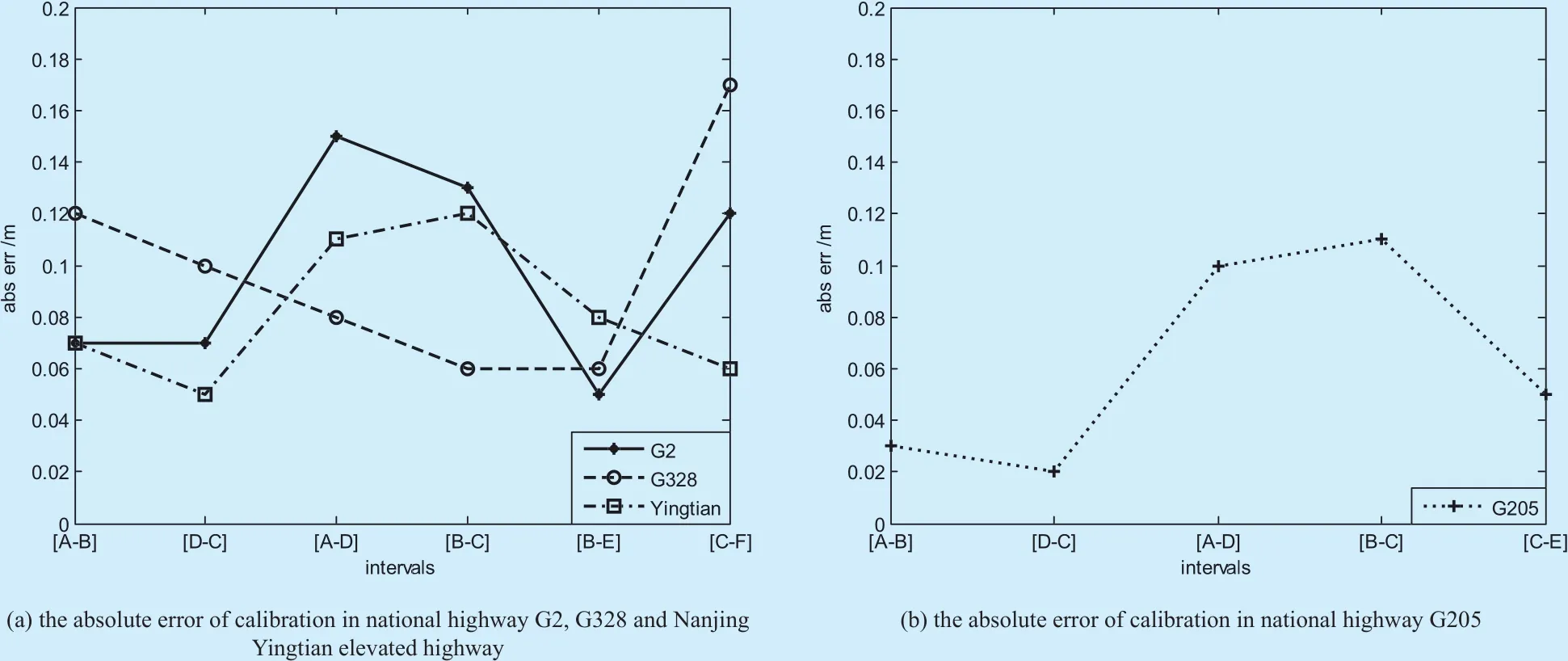
Fig. 8. Error analysis of calibration experiments in four multi-lane scenarios.
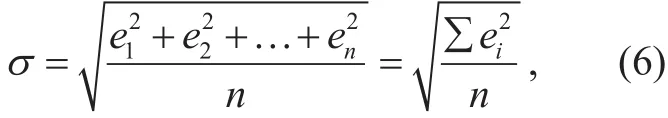
Where character eiis the absolute error listed in table 6, 7, 8 and 9 and n is the number of absolute errors. The standard errors of four multi-lane scenes are as follows: σG2=0.10,σG205=0.07, σG328=0.11, σYingtian=0.09. These standard errors are small enough for automatic calibration application. In addition, the accuracy and effectiveness of the proposed method is also been validated.
V. CONCLUSION
In this paper, we presented a precise information extraction algorithm for lane lines. The proposed method performs well in solving the occlusion of lane lines in traffic surveillance scenes, left and right edges extraction as well as endpoints extraction of lane lines. Experiments implemented on both single-lane and multi-lane scenarios show that our method performs better than the other three methods.In addition, the average correct rate of our experimental results of multi-lane scenes is 92.20%, and the standard errors of our lane line calibration experiments in the above multi-lane scenes are as follows: σG2=0.10,σG205=0.07, σG328=0.11, σYingtian=0.09. All these experiments demonstrate our method’s accuracy and effectiveness. In the future, we will attach more focus to the research of improving time efficiency.
ACKNOWLEDGEMENT
We are very grateful to reviewers who have reviewed drafts and made valuable comments.This work is supported by the National Nature Science Foundation of China under Grant No.61502226; the Jiangsu Provincial Transportation Science and Technology Project No.2017X04; the Fundamental Research Funds for the Central Universities.

Algorithm 1. The detailed pseude-code.Input: two different line segments (Point (S1.x, S1.y) of L1, Point (S2.x, S2.y)of L2)Output: left and right edges of certain lane line Begin Calculate the distance of starting points If distance < benchmark value If S1.x < S2.x L1 is the left edge of the lane line L2 is the right edge of the lane line Else L1 is the right edge of the lane line L2 is the left edge of the lane line End End End
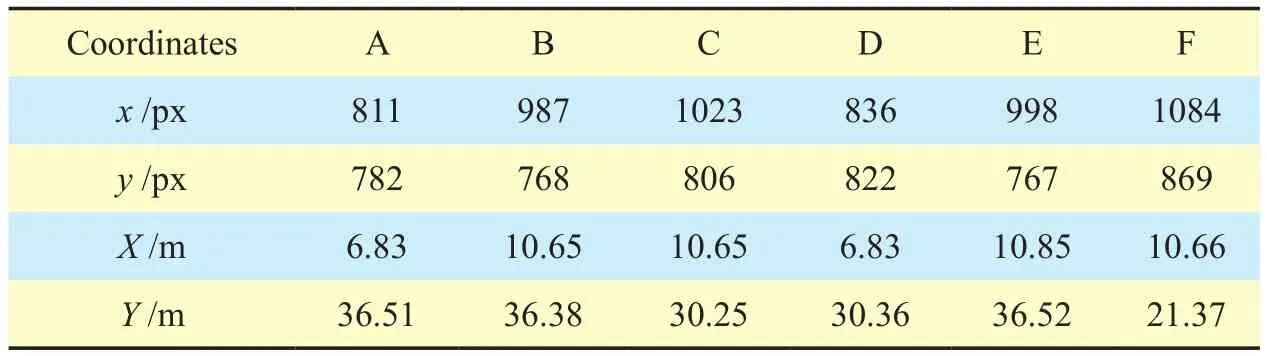
Table II. World coordinates of the points in Fig.7 (a).
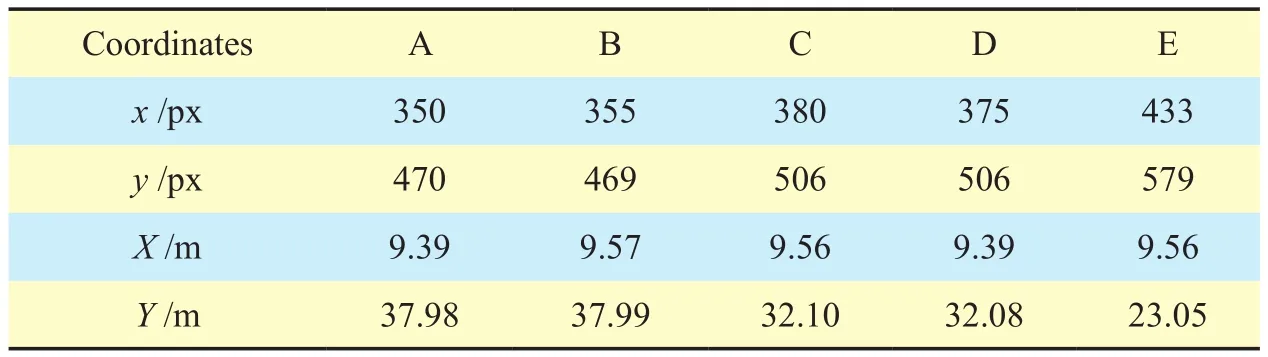
Table III. World coordinates of the points in Fig.7 (b).
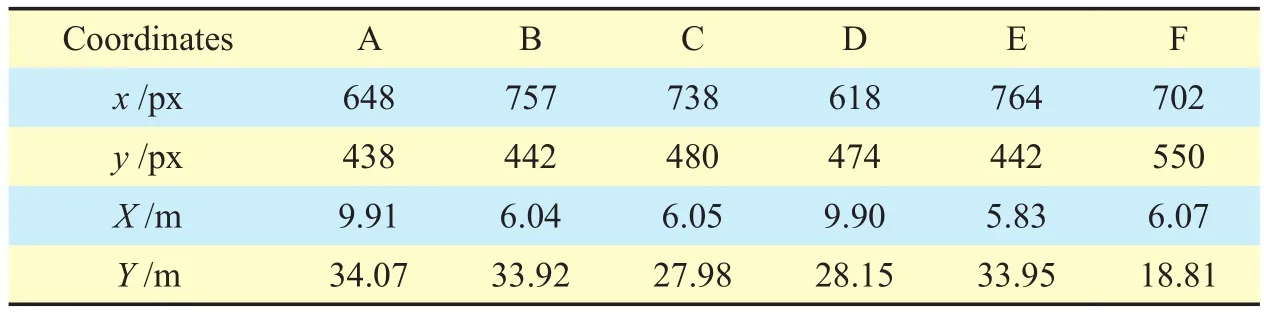
Table IV. World coordinates of the points in Fig.7 (c).
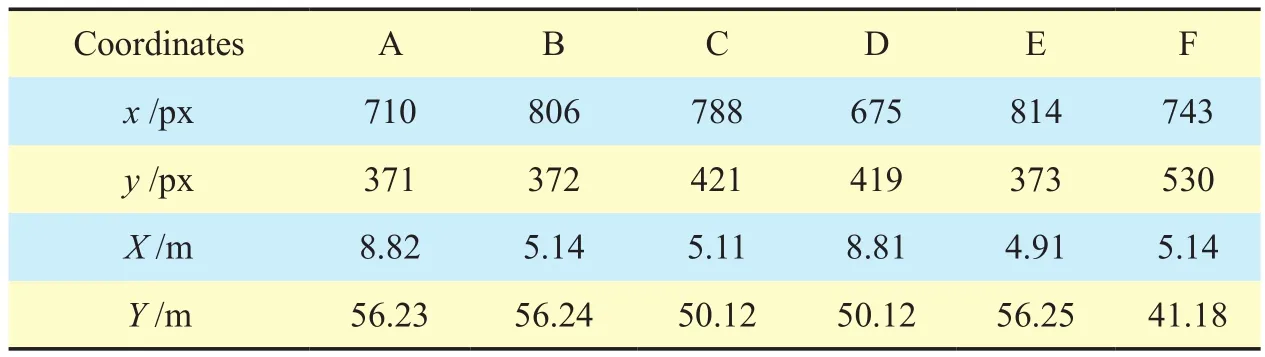
Table V. World coordinates of the points in Fig.7 (d).
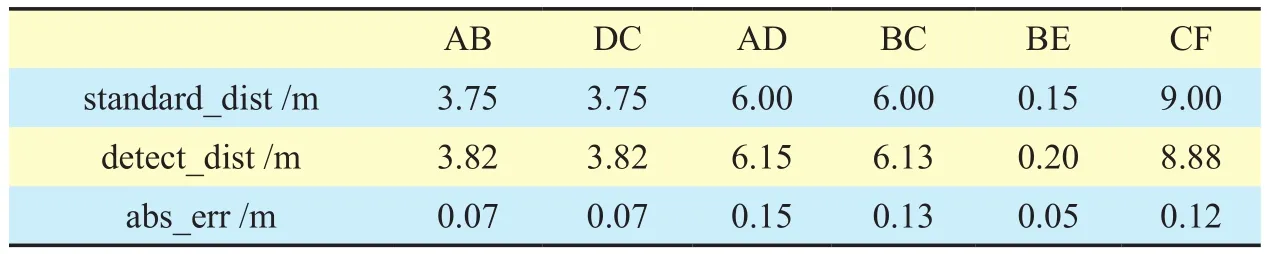
Table VI. Detect distances of each interval in table II.
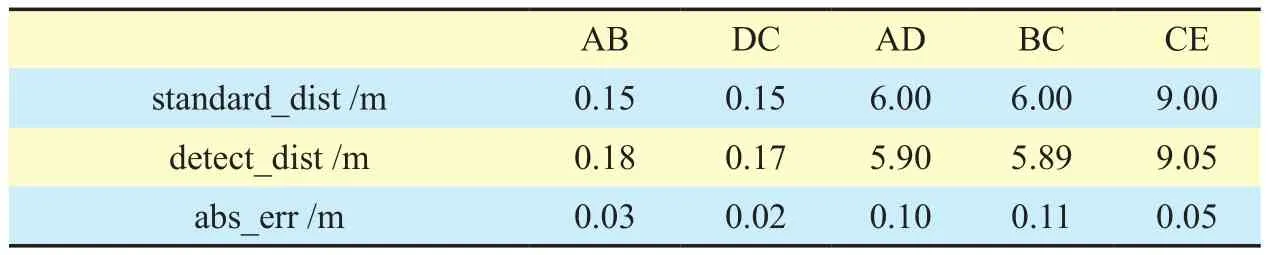
Table VII. Detect distances of each interval in table III.
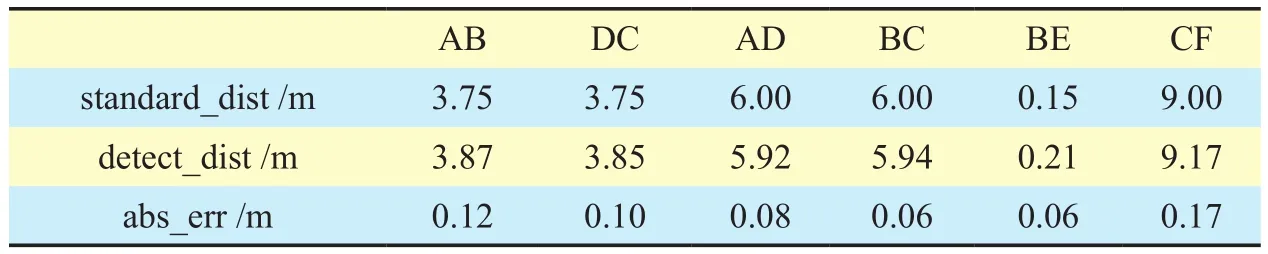
Table VIII. Detect distances of each interval in table IV.
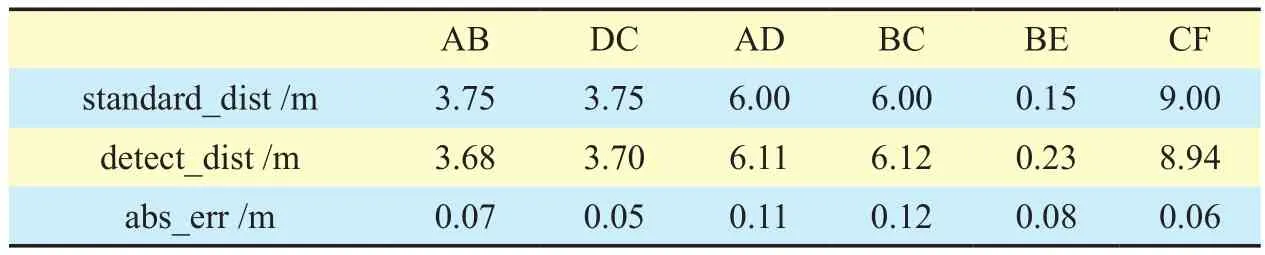
Table IX. Detect distances of each interval in table V.
- China Communications的其它文章
- Energy-Efficient Multi-UAV Coverage Deployment in UAV Networks: A Game-Theoretic Framework
- An Efficient Algorithm for Skyline Queries in Cloud Computing Environments
- Cryptanalysis of Key Exchange Protocol Based on Tensor Ergodic Problem
- Physical-Layer Encryption in Massive MIMO Systems with Spatial Modulation
- A Robust Energy Efficiency Power Allocation Algorithm in Cognitive Radio Networks
- SVC Video Transmission Optimization Algorithm in Software Defined Network

