Lang Ruan, Jinlong Wang, Jin Chen,＊, Yitao Xu, Yang Yang, Han Jiang, Yuli Zhang, Yuhua Xu

1 College of Communications Engineering, Army Engineering University of PLA, Nanjing, 210000, China

2 Key Embedded Technology and Intelligent System Laboratory, College of Information Science and Engineering,Guilin University of Technology, Guilin 541006, China.

Abstract: UAV cooperative control has been applied in many complex UAV communication networks. It remains challenging to develop UAV cooperative coverage and UAV energy-efficient communication technology.In this paper, we investigate current works about UAV coverage problem and propose a multi-UAV coverage model based on energy-efficient communication. The proposed model is decomposed into two steps: coverage maximization and power control, both are proved to be exact potential games (EPG) and have Nash equilibrium (NE) points. Then the multi-UAV energy-efficient coverage deployment algorithm based on spatial adaptive play(MUECD-SAP) is adopted to perform coverage maximization and power control, which guarantees optimal energy-efficient coverage deployment. Finally, simulation results show the effectiveness of our proposed approach,and confirm the reliability of proposed model.

Keywords: UAV networks; multi-UAV coverage; energy-efficient; potential games; Nash equilibrium

I. INTRODUCTION

Over the past decades, unmanned aerial vehicle (UAV), popularly known as drones, has been developing rapidly. Based on their main characteristics of small volume, strong mobility and low communication overhead, UAVs have been widely utilized in military, public and civil applications [1]–[3]. However, single UAV often fails to meet the needs of complicated missions, which may prevent it from being used in large-scale applications. To address the issue, it requires to form a cooperative UAV group to improve efficiency, especially in information collection and processing. For instance, the authors in [4] established a mathematical model of multi-UAV cooperative investigation. A cooperative investigation model based on target detection, identification and detection time was studied in [5]. The above studies shows that the cooperation of UAVs has become one of the key technologies in UAV networks.

It is worthwhile mentioning that a lot of works so far have been focused on area coverage problem [6]–[10], because most mission-driven UAV communication technologies can eventually convert into the practical application under area coverage problem. Hence,under the circumstance of cooperative UAV control coverage, missions such as investigation, communication and mapping can be well accomplished. The ratio of coverage area and given area tends to be a basic measurement of coverage ability of UAV network [6]. Besides,it makes coverage ability more specific and precise by adding impact factors for mission area. Authors in [6] introduced a static coverage in UAV networks when UAVs keep hovering in mission performing, which emphasizes the importance of wireless sensor network(WSN) in UAV coverage problem. Then, an exhaustive summary about static UAV coverage problem in WSN was discussed in [11].Recently, game theory has become one of the important approaches for multi-user distributed decision optimization in wireless communication [12]–[15]. In [16], authors developed a game theoretic formulation for multiple UAV cooperative search and surveillance, and designed constrained action sets of vehicles for preparation of deployment calculations. The interaction between multiple UAVs can be effectively studied from game theory, which provides theoretical support for relevant optimization methods in UAV networks.

In addition to coverage ability, there are still many challenges in UAV coverage problem, including mobility, lifetime, connectivity and obstacles. Lack of energy is a serious shortcoming of UAV, since a mission failure or even a crash of the drones may happen if the battery can’t support the drones to complete the mission. Therefore, energy-efficient UAV communication must be well studied in UAV networks [17]. When UAVs are performing mission-driven coverage, it can dramatically improve the ability of UAV to adapt to the environment and reduce communication and flight overhead so as to avoid severe consequences. It is noted that under related UAVs’collaborative impact, UAV coverage mission can be well accomplished. However, multi-UAV collaborative coverage is rarely studied,since the cooperative relationship is hard to describe.

Researches have been done to study UAV coverage problem. Authors in [18] investigated energy-efficient UAV communication with a ground terminal by designing a paradigm which considers UAV’s energy consumption and communication throughput, and also defined the energy efficiency of UAV communication; In [19], authors derived the coverage probability function for a ground user from a given UAV, which consists of antenna gain and altitude.

To solve energy-efficient problems better under area coverage scenario, we first build a multi-UAV collaborative coverage scenario.Then, the coverage deployment based on energy-efficient communication between multiple UAVs is proposed in this paper. Unlike traditional coverage approach, we adopt coverage probability to describe a successful coverage,and utilize the cooperative relation of drones.Firstly, priori information including mission area and UAV states is given. Secondly, the ground command center perform calculation of coverage maximization and power control;Finally, cooperative drones receive decision results, adjust their carrier power and reach designated deployment area cells to perform communication mission. While modeling coverage probability, we take the signal antenna gain and path loss into account.

The main contributions of this paper can be summarized as follows:

? An energy-efficient multi-UAV coverage deployment model is constructed to accurately describe the cooperative relationship between UAVs. By adopting the concept of soft coverage, we consider related UAVs’collaborative impact and better define a success coverage, which makes the coverage scenario more realistic and efficient.

? By employing the centralized-distributed optimization architecture, an effective solution is designed to solve the multi-dimensional strategies problem, which is divided into coverage maximization and power control, so as to reduce the complexity of strategy selection. Meanwhile, we model the proposed model as a game-theoretic framework and prove the existence of Nash equilibrium point.

? Multi-UAV energy-efficient coverage deployment algorithm based on spatial adaptive play (MUECD-SAP) is designed to achieve the NE point of the proposed method, which can efficiently explore theoptimal solution. Meanwhile, convergence of the proposed algorithm was also proved.

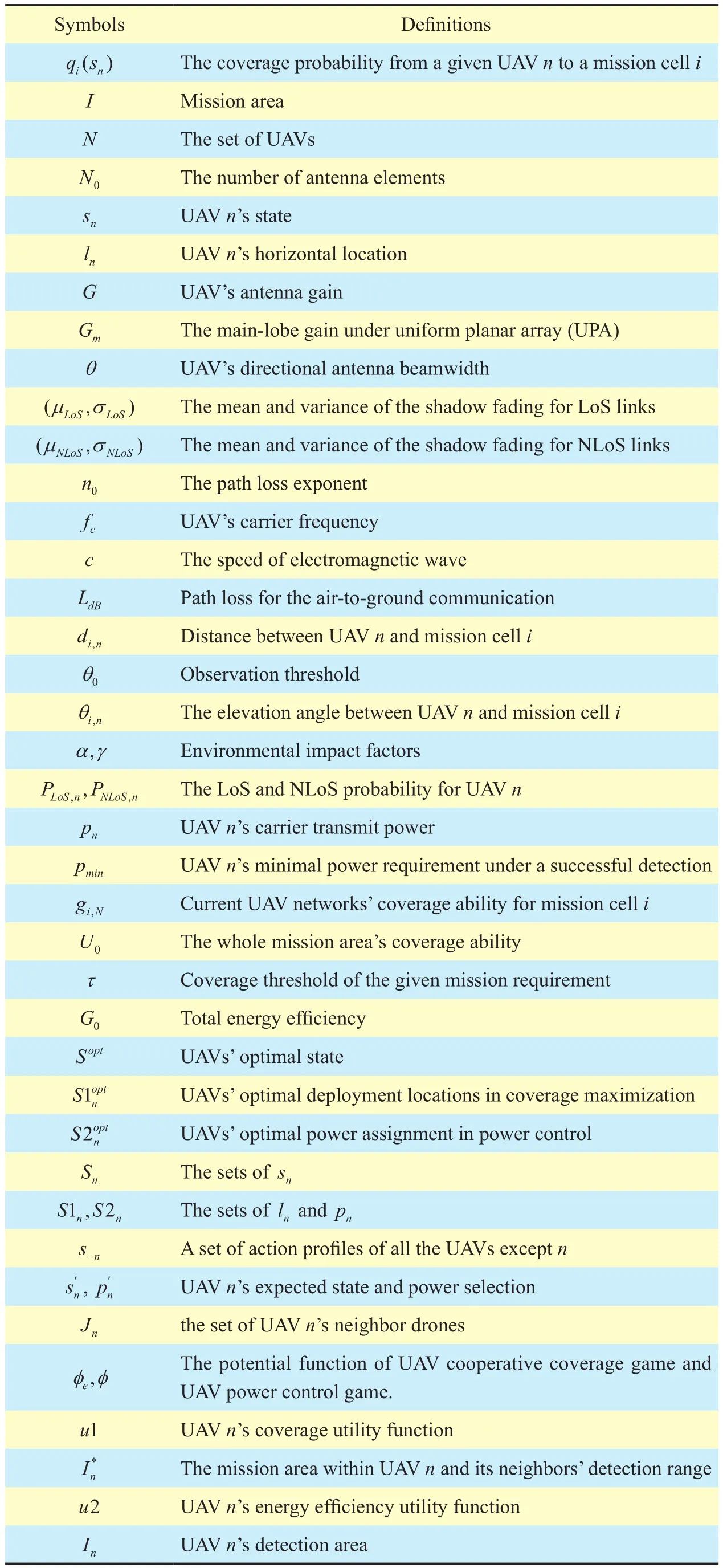
Table I. Notations and symbols used in this paper.

Note that our work adopts the concept of coverage probability from [19] and utilizes it for modeling. The main differences can be summed up to: (i) Unlike using a specified threshold to determine it whether or not a successful coverage, we modify coverage probability function by combining the coverage probability of multiple related UAVs, which makes the UAV coverage more precise and efficient. (ii) We consider the energy efficiency communication of given number of UAVs by transmission power control and location adjustment, while potential game approach is adopted to analyze the model and support our work.

The rest of the paper is organized as follows. Section II presents the system model and problem formulation. In section III, a game-theoretic framework to multi-UAV coverage is modeled and analyzed. The simulation results are reported in section III-D, which also makes some discussions on the simulation results and look into the distance some follow-up work. The final concluding remarks is given at last.

II. SYSTEM MODEL AND PROBLEM FORMULATION

We consider a multiple UAV cooperative coverage problem, as shown in figure 1. For the ground unit i, we assume the coverage probability from a given UAV j is qj,i, then we adopt the concept of soft coverage and calculate i’s coverage probability in UAV networks and derive the formula as follows:1?(1?q1,i)×(1?q2,i)×(1?q1,i). This formula indicates that the more number of UAVs detect, the higher coverage probability i ground unit will get, which tends to be reasonable and realistic.

Given the factors of antenna gain and path loss, how to accurately describe a mission point’s coverage utility is an issue worth pondering. Here we consider an air-to-ground network consisting a set of UAVs N. The continuous area I∈R2is uniformly meshed and divided into discrete cells. UAV n’s state is defined as sn={ln,pn}, where lnand pnrepresents UAV n’s horizontal location (xn,yn)and carrier transmission power. Suppose fixedwing drones fly horizontally in a stationary low altitude platforms (LAPs) [20]. UAV’s directional antenna beamwidth is denoted by θ=2π/, which corresponds with the antenna pattern under uniform planar array(UPA)[21], then we have UAV’s antenna gain:

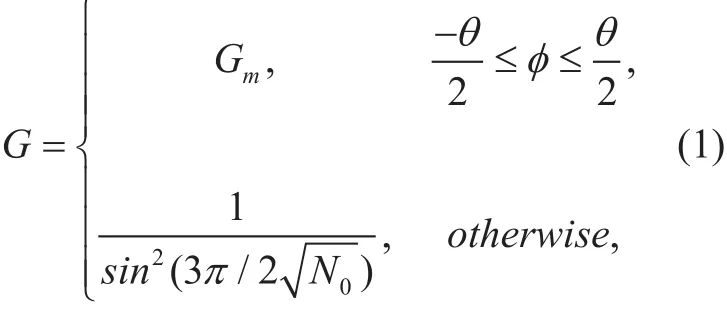
where Gmrepresents the main-lobe gain and is equal to the number of antenna elements N0. Moreover, the second item is the sidelobe gain.

According to [22], the coverage probability is jointly determined by the path loss, location,carrier transmission power, and environmental impact factor. To begin with, the air-to-ground communication’s path loss LdBis given by:

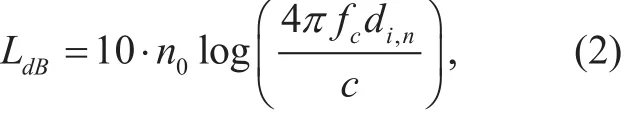
where n0represents the path loss exponent, fcis the UAV’s carrier frequency, c is the speed of electromagnetic wave, di,nrepresents the distance between UAV n and mission cell i.

Secondly, due to the imperfect wireless transmission, there are LoS (line-of sight)and NLoS (non-line-of sight) links. Specifically, the LoS probability is determined by, where θ0is the observation threshold, representing the minimum elevation angle to receive signal from the LAP for a UAV. Furthermore, α and γ are constants, which are environmental impact factors. Thus, the NLoS probability is PNLoS,n=1?PLoS,n.

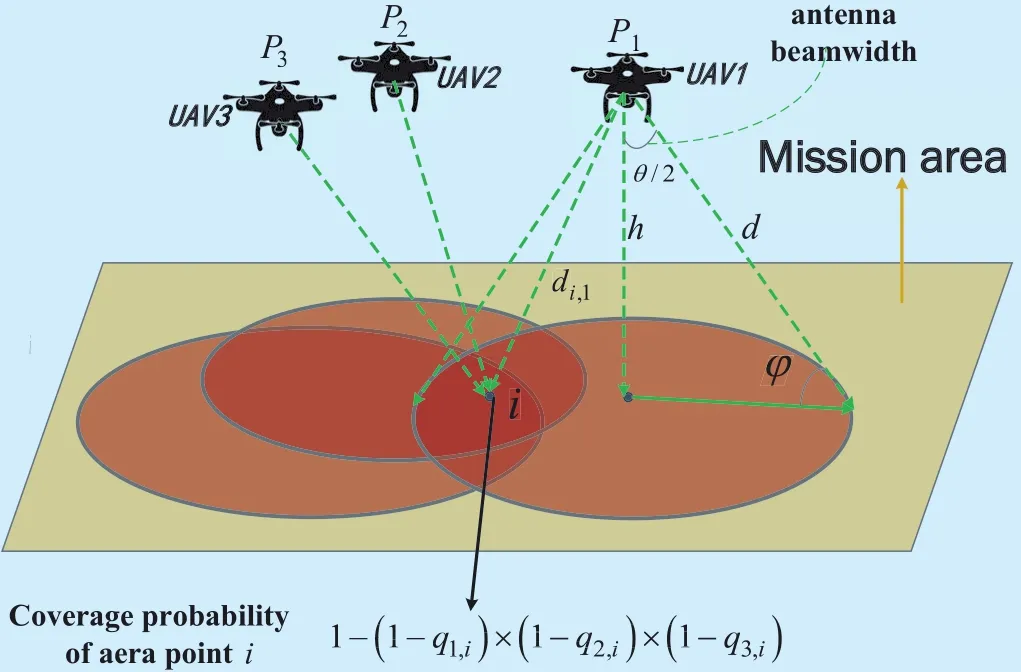
Fig. 1. A diagram of multi-UAV coverage in a mission area.

Finally, the coverage probability of a single UAV n to a mission cell i can be derived as follows [19]:

where pnrepresents UAV n’s carrier transmission power, and pminis the minimal power requirement under a successful detection,(μLoS,σLoS) and (μN(yùn)LoS,σNLoS) represent mean and variance of the shadow fading for LoS and NLoS links respectively.

In order to study the aggregate coverage effect of the whole mission area, we introduce the concept of mission area importance. Accordingly, the current UAV network’s coverage ability for mission cell i is given by:

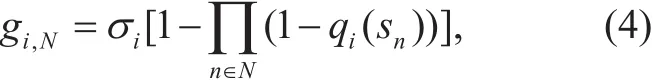
where σireflects the importance (traffic, etc)of mission cell i. Hence, we further derive the whole UAV network’s coverage ability:

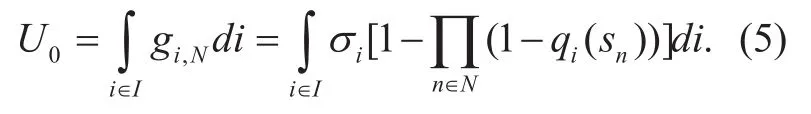
Note that UAVs perform coverage missions with their carrier transmission powers, saving energy consumption is of great concern. On the other hand, the coverage requirement must be satisfied to ensure the mission completion quality. Motivated by the energy efficiency design of UAV communication in [18], the UAV network’s total energy efficiency G0is denoted as follows:

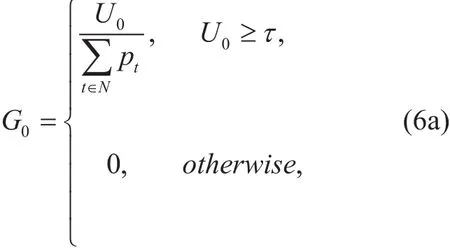
where τ stands for coverage threshold of the given mission requirement. Moreover, the energy efficiency G0reflects the coverage utility per unit power. Specifically, higher G0implies less transmission power, and higher coverage utility can be obtained. Hence, the object of this model turns to find an optimal UAV state Soptto maximize G0:

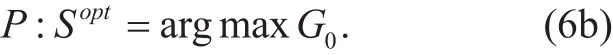
III. A COOPERATIVE GAME-THEORETIC FRAMEWORK

Given that the proposed system model involves multiple discrete variables, an effective solution is required to address the challenges of heavy computation complexity caused by huge strategy spaces.

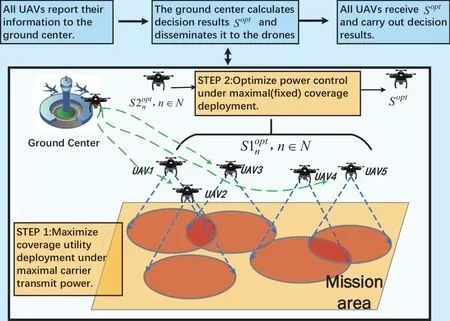
Fig. 2. A dimensionality reduction method for solving problem P.

Inspired by the advances in wireless cloud technologies, authors in [23]–[25] established a centralized-distributed optimization architecture for small cell networks, and map the physical cell network into a virtual decision network in the cloud, in which the proposed problem is solved by an optimization solution.The above works provide a reference for us to solve the proposed model.

First of all, in the centralized aspect, the environment parameters of mission area and all drones’ information, e.g., locations, carrier transmission powers, and coalition preferences are reported to the ground center, in which the UAV network is mapped to the virtual decision network. Then, an optimization approach is designed to solve the problem; Finally, the obtained decision results Soptwill be disseminated to drones, which will adjust their carrier transmission powers and fly to the designated positions according to Sopt. The blue block diagram of figure 2 shows the above steps.

3.1 Dimensionality reduction solving process

Note that solving P is challenging due to the multi-dimensional strategies (locations and transmission power), a dimensionality reduction method is taken into account by dividing P into P1 and P2, so as to reduce the complexity of strategy selection. Fig. 2 shows a dimensionality reduction method for solving problem P:

Step 1 (Coverage maximization): According to Eq. (5), exploring UAVs’ optimal deployment locationswith their given maximum carrier transmission powers:

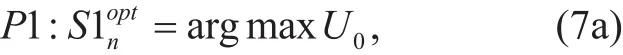
Step 2 (Power control): Determine whether the UAV network’s current coverage utility U0satisfies the communication requirement.If not satisfied, P has no solution; Otherwise,calculate the optimal power assignmentto maximize total energy efficiency with current UAV states=?, where ?represents Cartesian product. Therefore, we have the following equation:

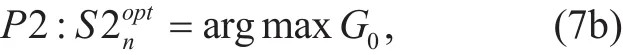
Proof work will be performed in the next section that both P1 and P2 has optimal solution which can be obtained. Finally, the ground center disseminates the decision results to the drones.

3.2 Cooperative coverage game in UAV coverage maximization

The last subsection provides an effective approach to solve problem P. However, both problem P1 and P2 are discrete optimization problem and NP-hard, which can not be efficiently solved by conventional centralized approaches, especially the number of mission cells is large. To address this challenge, we adopt game theory [26], which is an effective tool for distributed multi-decision problems where the individual decision mutually influences each other. Authors in [27] describe some cooperative relations of multi-agent game. Besides, the self-determined characteristics of game theory also make it widely applied to UAV networks in [28]–[30], which inspire us on solving the proposed problem.

In this subsection we focus on game-theoretic framework for energy-efficient multi-UAV coverage deployment model. The coverage problem is modeled as a strategic form game: R(N,I,{Sn,n∈N},{Un,n∈N}). For convenience, we also set location lnand transmission power pnas an element of S1nand S2n, that is, S1n?S2n=Sn. Meanwhile, we define s?nas a set of action profiles of all the UAVs except n. Un=U1n?U2nrepresents the utility function of coverage maximization and power control, where ? represents Cartesian product. sn, u1nand u2nare denoted as an element of Sn, U1nand U2n. Therefore,the proposed energy-efficient multi-UAV coverage deployment model turns out to be a cooperative game, in which the utility of a player(UAV n) rests with both its and other drones’states in the networks.

Basic definitions of potential game was introduced [31]–[33], indicatingg the potential game requires players take cooperative control in distributed multi-agent systems, making each player’s localized utility to be associated with global utility. The following definitions is firstly introduced to analyze the properties of the formulated game-theoretic framework.

Definition 1 (Nash Equilibrium (NE)[34]).

A state selection profile S*=(,…,) is a pure strategy NE if and only if no player n can improve its utility by changing its states, i.e.,

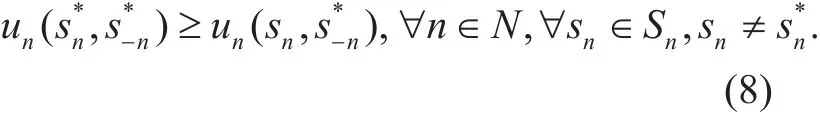
Definition 2 (Exact Potential Game[31]).For utility functions u(sn,s?n), if there exists a potential function φ, for arbitrary strategy selection changes from snto, the following equation is true:

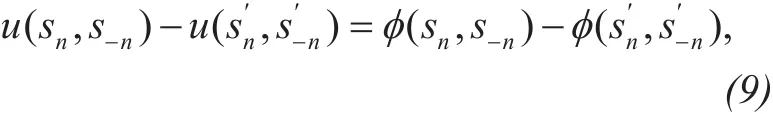
then this game is called exact potential game(EPG) and has at least one NE point.

In the step of coverage maximization, given that the proposed model focuses on cooperative UAVs, those UAVs which exist overlapping detection areas tend to have cooperative behaviors. Motivated by local altruistic game[34], what the strategy a UAV decides to make depends on both itself and its neighbors. As figure 3 depicted, UAV 1’s change of location affects not only its utility, but also those drones whose reconnaissance mission area overlap UAV 1’s. Hence, we construct the model as a cooperative coverage game, what the strategy UAV 1 decides to make depends on both itself and its neighbors’ current and predicting location change. It can be seen that parts of UAV 2 and UAV 3’s detectable area is within UAV1’s detection range, which makes them UAV 1’s neighbors. What a strategy UAV 1 select affects the area painted in blue,which also lead to the change of coverage utility in the other two UAVs.

Here, we define Inas UAV n’s detectable area, then Jnshould be the set of n’s neighbor drones as long as In∩IJn≠0, which satisfies the above description. We also denoteas UAV n’s new neighbor drones after n selects a new location. Note that all drones carry their maximal transmission powers, the utility function based on cooperative coverage game in coverage maximization can be expressed as follows:

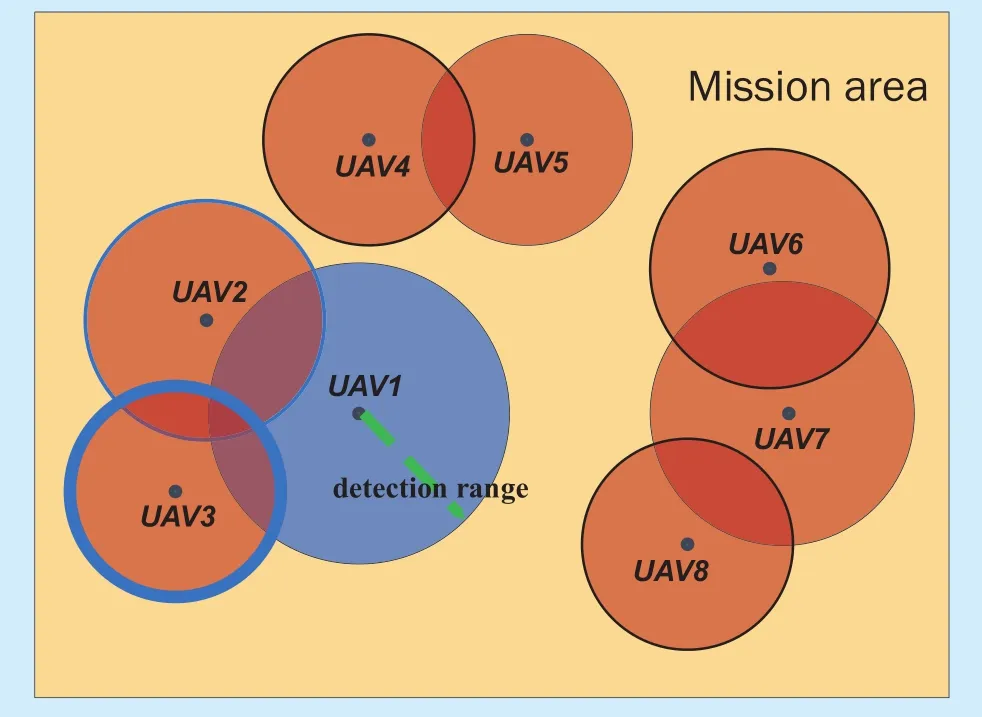
Fig.3. A diagram of relationship between UAV 1 and its neighbors.

According to object G1, the optimal local utility of UAV n was determined by n’s horizontal location.

Theorem 1.Consider the multi-UAV coverage problem formulated as a cooperative coverage game, player take Eq. (10) as its utility function. The cooperative coverage game G1 is an EPG, and has at least one pure strategy NE point. In addition, the optimal solution of coverage maximization P1 is the pure strategy NE point of G1.

Proof: Firstly, we construct the whole coverage utility as potential function, that is:

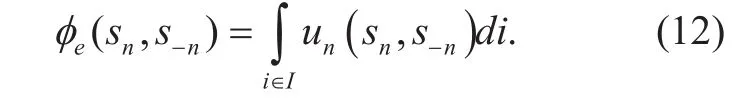
Suppose that an arbitrary UAV n changes its state from sntoin one step move, we calculate the change of the potential function caused by individual strategy selection as follows:

Intuitively, UAVs which are not in J1nare completely unaffected by above strategy changes. Therefore, the result of the last two items from Eq.(13) is identically zero. In that case, we conclude from Eq. (10) and Eq. (13)that:

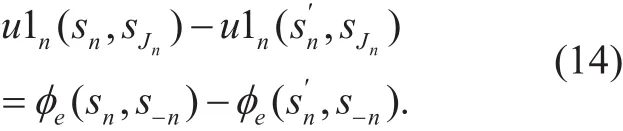
Therefore, we learn from Eq.(14) that as arbitrary UAV change its action strategy, the change value of its local utility function and potential function are the same. Thus, the local altruistic game G1 is proved to be an EPG,and has at least one pure strategy NE point according to definition 2. Notably, the designed potential function refers to whole coverage utility, which guarantees each player’s current local utility is associated with the global coverage utility. Hence the optimal solution of P1 turns to be the pure strategy NE point of G1.

3.3 Potential game in UAV power control

As can be seen from the construction of Eq.(3), the coverage probability for the ground cell from UAVs is not only determined by UAVs’ location, but also closely related to their carrier transmission power. Fig. 4 shows that for a given UAV, transmission power can distinctly influence coverage probability under a fixed UAV deployment. Here we take ground mission cell (5,30)(×200m) for instance, and capture two UAVs of different locations for comparison. There are two distinctive features from the figure: (1) Two curves in this figure demonstrate that the more transmission power an UAV carry, the higher coverage probability a successful coverage will occur to the ground cell. (2) As we increase transmission power,the coverage probability will approximate the peak and gradually flattens out.

Note that under the current fixed UAV deployment, one drone’s power selection affects its detectable mission area cells’ coverage probability. For the above description, the power control problem is modeled as a potential game. We construct UAV n’s individual utility function to capture optimal transmission power assignment based on potential game by utilizing Eq.(6a):

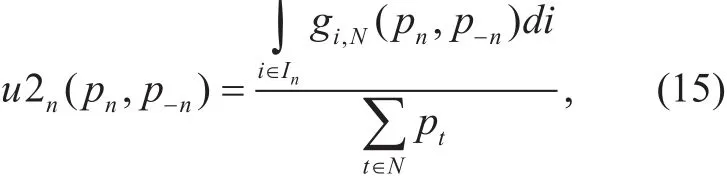
where Inrepresents UAV n’s detection area.Eq.(15) indicates the optimal energy efficiency of UAV n under fixed optimal location, which is determined by n’s carrier transmission power.

In this process, the utility function with corresponding parameters also satisfy the characteristic of potential game, making each player’s localized utility to be associated with global utility. As a consequence, the designed UAV power control model can be able to constitute a potential game:

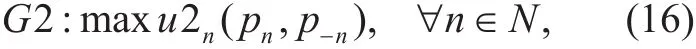
Theorem 2.Consider the multi-UAV optimal power control problem, player take Eq.(15) as its individual utility function. Then the UAV potential game G2 is an EPG, and has at least one NE point. In addition, the optimal solution of problem P2 are pure strategy NE of G2.

Proof: Firstly, the energy efficiency utility is denoted as potential function, which is given by:

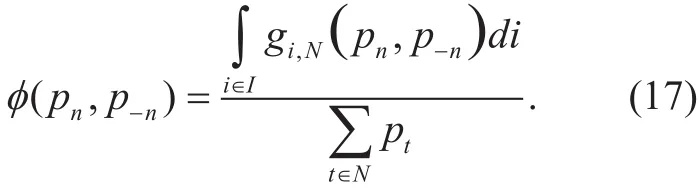
Same as the above, for arbitrary transmission power selection changes from pnto,we calculate the change of the potential function as follows:

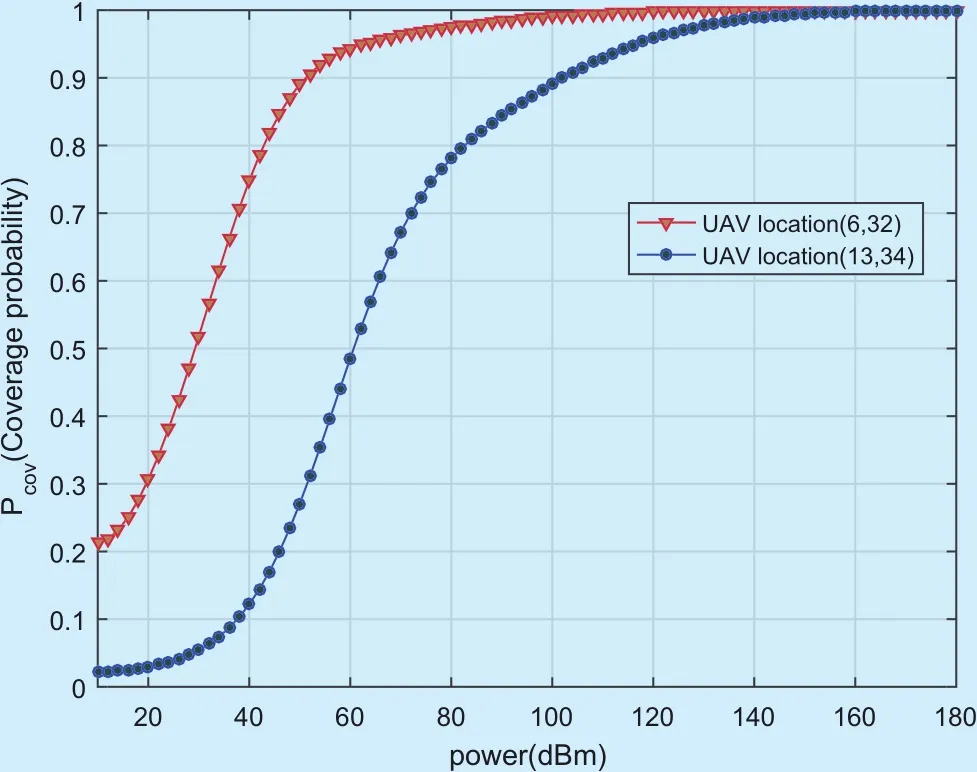
Fig. 4. Coverage probability for a ground mission cell(5,30)(×200m) from a given UAV considering transmission power.

It should be pointed out that the mission area which is not within the UAV n’s detection range is completely unaffected by above strategy changes. Therefore, the following formula holds:

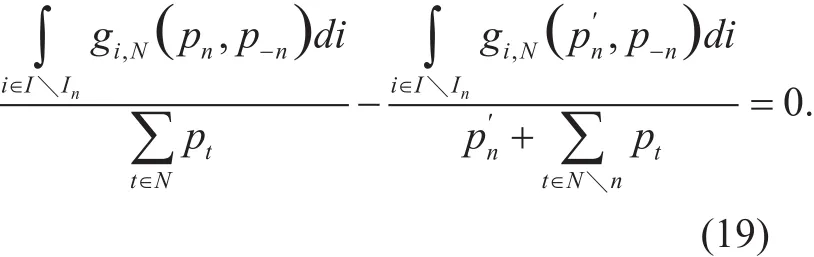
Note that Eq. (18) and Eq. (19), for arbitrary UAV n, the change value between its potential function and individual utility function are the same as UAV n change its transmission power strategy, i.e.,

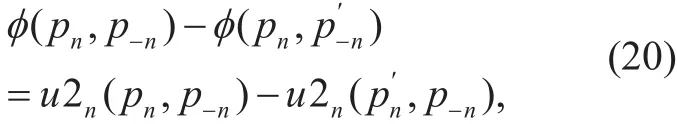
which indicates that G2 is an EPG according to definition 1, and has at least one pure strategy Nash equilibrium point. Besides, the designed potential function refers to whole coverage utility, which guarantees each player’s current individual utility is associated with the whole coverage utility. Hence, the optimal solution of problem P2 are pure strategy NE of G2.

?

3.4 Multi-UAV energy-efficient coverage deployment algorithm based on spatial adaptive play

As the multi-UAV energy-efficient coverage deployment problem now formulated as an EPG, learning algorithms need to be applied to explore the Nash equilibria of game, so as to prevent UAV strategy selection from falling into trap, that is to say, local optimum. Algorithm 1 demonstrates procedures of multi-UAV energy-efficient coverage deployment algorithm based on spatial adaptive play(MUECD-SAP). Binary log-linear learning[35] was proved to guarantee convergence to the optimal Nash equilibrium, being used to explore UAVs’ optimal coverage deployment inspired by [16]. Here we design Eq. (21) as UAVs’ action selection probability function,where t represents iteration number. Consider the complexity of multi-agent decision mechanism, a distributed learning algorithm is required in power control. Therefore, spatial adaptive play (SAP) [34] is adopted to converge transmission power to the stable allocation state. In Eq. (22), qn(t ) represents the power selection probability function of UAV n. β is the learning parameter (β ＞ 0).

IV. SIMULATION RESULTS AND DISCUSSION

In this section, we carry out simulation to evaluate the effectiveness of our proposed approach. For parameter settings mentioned in section II, we consider the UAV-based communications network from [22] for urban en-vironment at carrier frequency of 2,000 MHz with μLoS=1 dB, μN(yùn)LoS=20 dB, α=0.6,γ=0.11 and n0=2.5. Given the proof and derivation in [22], we obtain pminand the following formula σLoS(θj)=k1exp(?k2θj),σNLoS(θj)=g1exp(?g2θj), where(k1,k2)=(10.39, 0.05), (g1, g2)=(29.06, 0.03).Moreover, we assume each UAV is equipped with N0=16 antennas [21]. Considering the actual requirements of the quadrotor UAVs,we set some reasonable discrete transmission power selections for aircrafts, that is, pn=(32,34, 36, 38, 40, 42, 44, 46, 48, 50) (dBm), n∈N. Here we set coverage threshold τ=0.6,that is to say, the whole coverage utility under determined strategy must be greater than or equal to 0.6 to meet the communication needs. In the following subsection, simulation process are divided into two steps to perform calculation according to the algorithm design.Assume the UAV flying altitude is fixed and equals to 500 (×200m).

Suppose the priori information of the mission area is known, here we uniformly divide mission area into 50×50 cells (the length of each cell is 200m) and designed probability density function (PDF) of the mission area, which obeys the normal distribution. Fig.5 shows the color-coded display of the density map for the mission area, then σiis defined as the product of normalized density and overall traffic data. Here we set(15,35),(35,15)(×200m) as central point of special areas, which play vital roles in coverage scenario and have done a great deal to influence the deployment of UAVs.

Fig.6 shows the change of total coverage utility U0considering different numbers of UAVs using MUECD-SAP algorithm. The result finally converges to a stable state when deploying 5 or more UAVs. However, coverage utility is less than 0.6 under the circumstance of deploying 4 UAVs, indicating it can not meet the demand of communication, so that the power control step can’t be carried out. Same result is shown in Table 2. In order to ensure the effectiveness and non-contingency of the results, we did 10 calculations for each deployment UAV number and obtain mean coverage utility.

Fig. 5. Density map of the mission area (×200m).

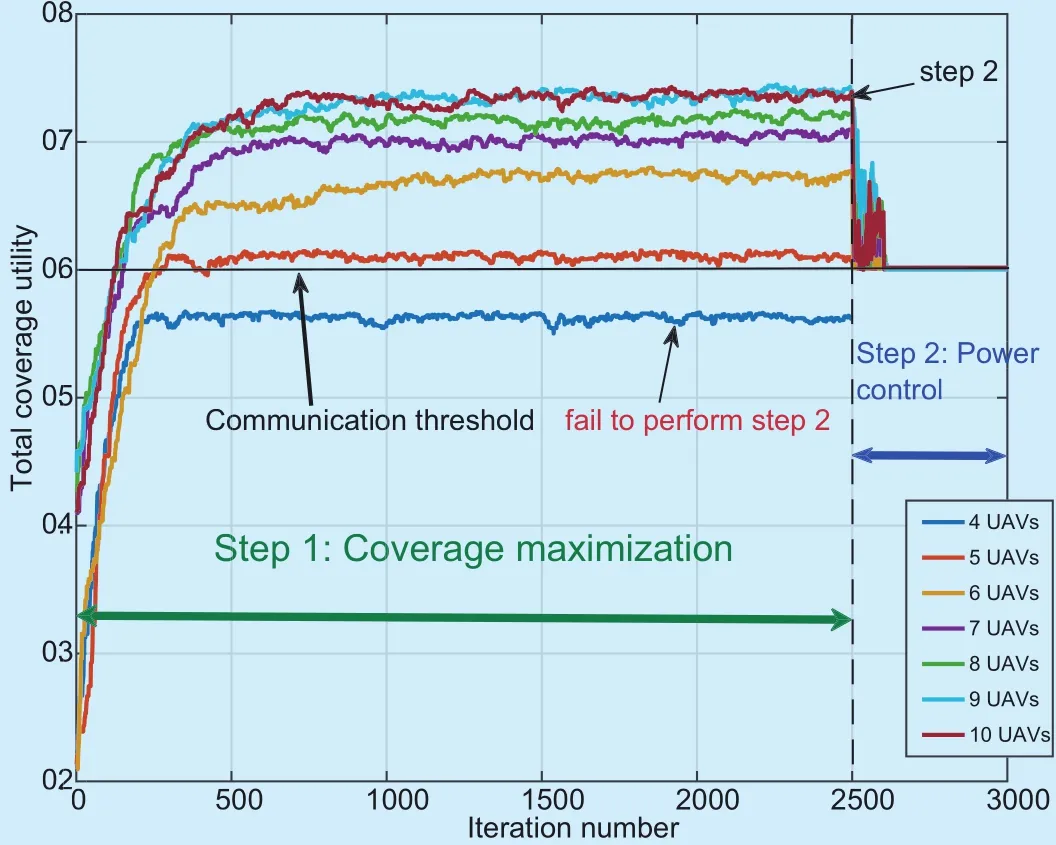
Fig. 6. The coverage utility considering different UAV numbers using MUECD-SAP algorithm.

It is also worthwhile mentioning that in both figure and table, when the number of UAVs increases to a certain number, the growth of coverage utility will be slow. We analyze that under the premise of special areas being firstly detected and covered, the new added UAVs can only detect and cover most of the remaining areas, resulting in low cover-age efficiency.

It should be pointed out that the numberof UAVs is given in advance, so as to satisfy coverage requirement. In order to better access the effectiveness evaluation of the proposed method, we decide to set the number of UAVs at 8 in the next simulation process.

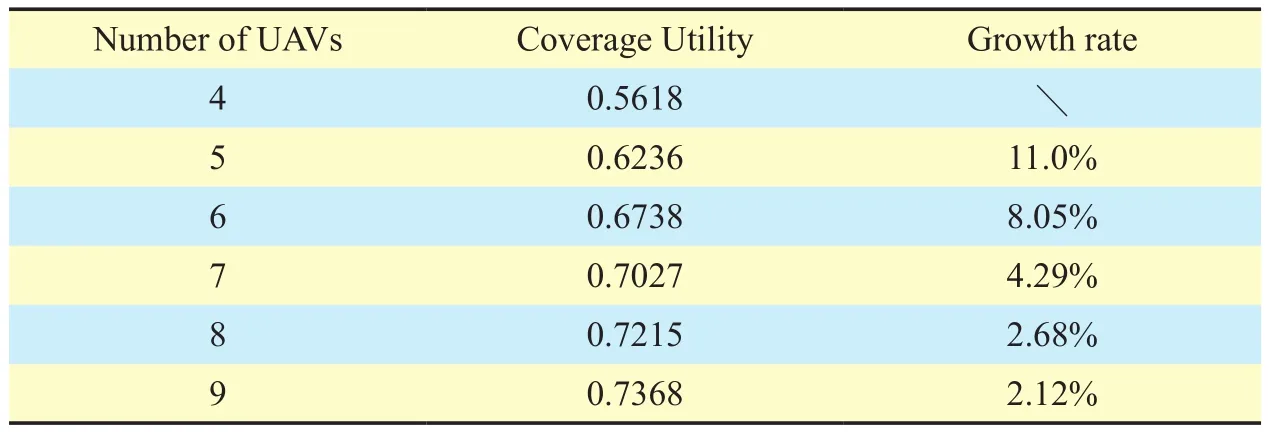
Table II. Optimal coverage utility with different UAVs numbers under maximum power.

In the following parts, we analyze and validate the effectiveness of simulation.

4.1 Optimal coverage under maximum power

Fig.7(a) shows the coverage probability map with 8 UAVs’ optimal coverage deployment with maximum carrier transmission power. It visibly characterize the situation where UAVs are deployed around the special areas, and this is supported by the expectation of more communication requirements. Intuitively, the closer a single UAV is to a special area, the higher its coverage performance is. What’s more, the color of overlap detection areas of UAVs is darker,confirms the previous analysis that the coverage probability can be increased under the cooperation detection of multiple UAVs. Meanwhile,different UAVs will not be deployed closely enough to ensure the coverage efficiency. All in all, simulation results prove the authenticity and reliability of the proposed model.

Fig.7(b) shows the convergence of total coverage utility U0using MUECD-SAP algorithm. To prevent contingency, we did ten operations of step 1. As can be seen from ten curves of step 1 in MUECD-SAP, we find out the total coverage utility converges to almost a certain value. The result proves that the proposed method has at least one Nash equilibrium point.

4.2 Optimal power control using SAP algorithm

Since simulation result satisfies the communication requirement, next we carry out UAV energy-efficient transmission power allocation.In the small figure of figure 7(b), we choose 10thcurve to perform step 2 in MUECD-SAP,the result also converges to a stable solution,which is very close to the communication threshold τ=0.6. This indicates the proposed MUECD-SAP algorithm can converge result to the NE point, which is supported by above theoretical analysis. What’s more, we also picture the final state of mission area covered by UAVs in optimal power assignment in figure 7(c), this is consistent with previous analysis.For further explanation, the convergence situation of UAV transmission power selection is also shown in figure 7(d), each curve represents the number of UAVs which select the corresponding transmission power. It suggests that each UAV learns through information interactions and explores power selections at the beginning, after about 110 iterations, every curve converges to stable states, proving the proposed power control method have at least one Nash equilibrium point.

The convergence situation of total UAV transmission power is indicated in figure 8,which considers different number of UAVs.Meanwhile, Fig. 9 shows the change of total energy-efficiency G0in iteration process. Both two figures confirm MUECD-SAP algorithm’s characteristic of distributed exploration learning, and more importantly, the effectiveness of convergence. What’s more, While exploring the optimal power selection strategy to maximal total energy efficiency in UAV networks,the total UAV transmission power overhead also tends to converge to the minimal result in the premise of satisfying the communication condition. It shows the importance of energy efficiency and confirms the effectiveness of MUECD-SAP algorithm.

4.3 Expansion and discussion

There is no denying that there are two cases for the mission area: covered and not covered. Notably, the proposed model primely simulates this scenario by using coverage probability to characterize the above two situations. Law of large numbers indicates that the frequency of a random event is approximately equal to its probability under constant conditions, which means in a large number of repeated occurrences of UAV detection events,the number of events which area to be covered tends to be almost certain.

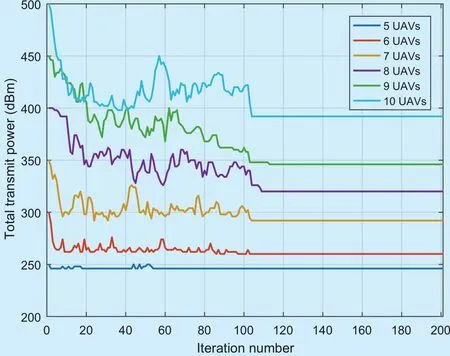
Fig. 8. The convergence of total UAV carrier transmission power.

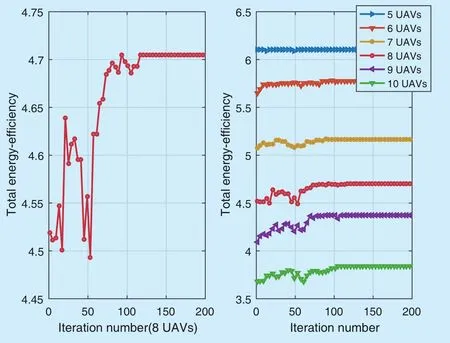
Fig. 9. The change of UAV total energy-efficiency G0 in iteration process.

It must also be mentioned that the proposed model assumes all UAVs communicated through the same carrier frequency, hence frequency interference Pminis considered and thus the UAV coverage performance is weakened. Given above issue, the frequency selection optimization is a significant and practical work, so as to improve the collaborative communication efficiency of UAVs.

Last but not least, what we study is an offline algorithm based on coverage and power optimization, but in the face of dynamic unknown scenarios such that obstacles and mission area change, the algorithm often loses its effectiveness. In fact, it remains challenging to online learning and there are relatively few studies devoted to it, owing to the mammoth computation that is generated by variable strategic spaces. Reinforcement learning (RL) is a novel and effective way to solve the decision problems in dynamic environment. Authors in[38] proposed an anti-jamming deep reinforcement learning algorithm to solve the problem of anti-jamming communications in dynamic and intelligent jamming environment. Therefore, RL has great potential in the dynamic UAV coverage scenarios, and is one of researches in our future work.

V. CONCLUSION

In this paper, we proposed a multi-UAV coverage deployment model based on energy-efficient communication in UAV networks. The multi-UAV coverage was a novel concept that reflects collaboration of UAVs and makes the coverage scenario more reliable and efficient.By introducing energy-efficiency, we built a UAV coverage scenario to solve the problem of energy shortages. The proposed model was decomposed into two steps: coverage maximization and power control, both were proved to be potential games and have at least one Nash equilibrium (NE) point, then the multi-UAV energy-efficient coverage deployment algorithm based on spatial adaptive play (MUECD-SAP) was adopted to perform motion and power control, which guaranteed suboptimal energy-efficient coverage deployment. Finally, simulations were performed to validate the effectiveness of our proposed approach,and confirmd the reliability of the proposed model. This research should thus has great potential for applications in actual multi-UAV cooperative communication scenario.

ACKNOWLEDGMENTS

This work was supported by the National Natural Science Foundation of China under Grant No. 61771488, in part by the Natural Science Foundation for Distinguished Young Scholars of Jiangsu Province under Grant No.BK20160034, and in part by the Open Research Foundation of Science and Technology on Communication Networks Laboratory, and the Guang Xi Universities Key Laboratory Fund of Embedded Technology and Intelligent System (Guilin University of Technology).