LIU Sheng-wang,LI Bing

(School of Sciences,Hebei University of Technology,Tianjin 300401,China)

Abstract:In this paper,we study the optimal investment-reinsurance problem in a risk model with two dependent classes of insurance business.Under the criterion of mean-variance,we aim to seek the corresponding time-consistent strategies within a game theoretic framework.By solving an extended Hamilton-Jacobi-Bellman system,the closed-form expressions of the optimal time-consistent investment-reinsurance strategies and the optimal value function are derived.Finally,some numerical illustrations are presented to show the impact of model parameters on the optimal strategies.

Keywords:equilibrium strategy;Hamilton-Jacobi-Bellman equation;mean-variance criterion;proportional reinsurance

1 Introduction

Nowadays,investment and reinsurance are playing increasingly important roles in insurance business.Optimal investment and reinsurance problems for insurers attracted much attention.Most existing works adopted the utility maximization or ruin probability minimization as objection functions.For example,Browne[1]considered a diffusion risk model and obtained investment strategies of maximizing the exponential utility or minimizing the probability of ruin.Yang and Zhang[2]studied the optimal investment strategies for an insurer to maximize the expected exponential utility of terminal wealth or maximize survival probability,where the surplus process is satisfied by a jump-diffusion model.Furthermore,Xu et al.[3],Gu et al.[4],Liang et al.[5]and Guan and Liang[6]investigated optimal investment-reinsurance strategies for an insurer to optimize the expected utility of terminal wealth in different situations.

Recently,optimal investment and reinsurance problems for insurers under the meanvariance criterion,introduced by Markowitz[7],drew much attention.For example,Bauerle[8]considered an optimal proportional reinsurance problem and got closed-form optimal strategy under mean-variance criterion,where the surplus process is modelled by classical Cramér-Lundberg model.Bai and Zhang[9]studied the optimal investment-reinsurance strategy for the mean-variance problem,where the surplus of the insurer is depicted by Cramér-Lundberg model and an approximated diffusion model.Zeng et al.[10]assumed that the surplus of an insurer is modeled by a jump-diffusion process,and derived closed form optimal investment policies by stochastic maximum principle under benchmark and mean-variance criteria.

However,it is a well-known fact that the mean-variance criterion lacks the iterated expectation property.As a result,stochastic control problem for mean-variance criterion is time-inconsistent,that is,a control maximizing the mean-variance utility at time zero may not be optimal at later time.In this case,Bellman optimality principle fails.The main difficulty when facing a time-inconsistent control problem is that,we cannot use the standard dynamic programming principle to characterize the Hamilton-Jacobi-Bellman equation in general.

Because the time-consistency of strategies is important for a rational decision maker,the main approach to obtain the time-consistent strategy is to formulate the problem within a non-cooperate game theoretic framework,where player t can be regarded as the future incarnation of ourselves at time t.Then we aim to derive the equilibrium strategy of the game.For more details,we refer the readers to Bjork and Murgoci[11],Bjork et al.[12],Ekeland and Lazrak[13],Ekeland and Pirvu[14],Krusell and Smith[15],Phelps and Pollak[16],Strotz[17]and references therein.However,as far as we know,there are a few literatures concerning equilibrium strategies for optimal investment and reinsurance problems under the mean-variance criterion.For example,Zeng and Li[18]are the first to present the optimal time-consistent investment and reinsurance strategies for mean-variance,where the surplus of the insurer is modelled by the diffusion model and the price processes of the risky assets are driven by geometric Brownian motions.Later on,Li et al.[19]studied the case with state dependent risk aversion and they derived equilibrium strategies via some class of well posed integral equations.Zeng et al.[20]considered the equilibrium investment and reinsurance strategies for mean-variance insurers with constant risk aversion where both the surplus process and the risky asset’s price process follow a geometric Lévy processes.Zhao et al.[21]considered an optimal time-consistent investment and reinsurance problem taking into account a defaultable security for an insurer under the mean-variance criterion in a jump-diffusion risk model.

Although the research on optimal investment-reinsurance for an insurer and meanvariance problem increased rapidly,only a few papers dealed with the investment-reinsurance problem with dependent risks.The research about dependent risks can be found in Liang and Yuen[22],Yuen et al.[23],Centeno[24],Bi et al.[25].

In this paper,we aim to derive optimal time-consistent investment and reinsurance strategies for the mean-variance insurers with constant risk aversion,where the surplus process is a dependent risk model and the financial market consists of one risk-free asset and one risky assets whose price process follows geometric Brownian motion.

The rest of this paper is organized as follows:in Section 2,the model and some assumptions are described;in Section 3,we formulate the optimization problem and provide a verification theorem;in Section 4,we derive the optimal time-consistent investment and reinsurance strategies and the optimal value function.Finally,some numerical illustrations and sensitivity analysis for our results are provided in Section 5.

2 The Model

Let(?,F,P)be a given complete probability space with a filtration{Ft}t∈[0,T]satisfying the usual condition,where T is a positive finite constant and represents the time horizon.All stochastic processes introduced blew are assumed to be well defined and adapted processes in this space.In addition,we suppose that the insurer has two dependent classes of insurance business such as motor and life insurance.

The surplus process of the insurer is modeled by

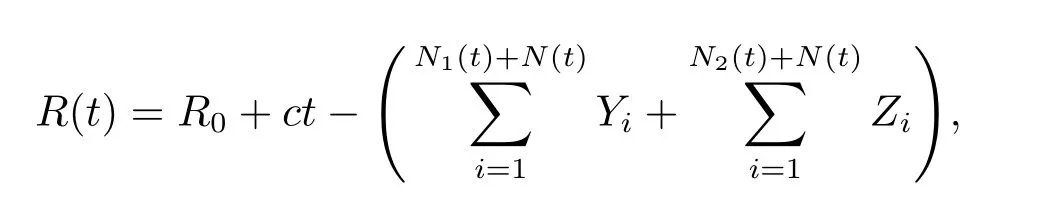
where R0is the deterministic initial surplus of the insurer and the constant c is the premium rate.N1(t),N2(t),and N(t)are three independent Poisson process with intensity parameters λ1>0,λ2>0,and λ >0,respectively.Yiis the claim size random variables for the first class with common distribution FY(·)and Ziis the claim size random variables for the second class with common distribution FZ(·);{Yi,i≥ 1}are assumed to be an i.i.d.sequence with E(Yi)= μ1Y>0 and E(Y2i)= μ2Y>0 and{Zi,i≥ 1}are assumed to be an i.i.d.sequence with E(Zi)=μ1Z>0 and E(Z2i)=μ2Z>0.Thus the compound Poisson process?S1(t):=represents the cumulative amount of claims for the first class in time interval[0,t]andrepresents the cumulative amount of claims for the second class in time interval[0,t].N1(t),N2(t),N(t),Yiand Ziare mutually independent.It is obvious that the dependence of the two classes of business is due to a common shock governed by the counting process N(t).Here,the premium rate is supposed to be calculated according to the expected value principle,i.e.,c=(1+ θ1)(λ1+ λ)μ1Y+(1+ θ2)(λ2+ λ)μ1Z,where θ1and θ2are the safety loadings of the insurer for the first class claim and second class claims,respectively.

Moreover,we allow the insurance company to continuously reinsure a fraction of its claim with the retention levels q1(t)(≥ 0)and q2(t)(≥ 0)for{Yi,i≥ 1}and{Zi,i≥ 1},respectively.It means that the insurer pays q1(t)Y(or q2(t)Z)of a claim occurring at time t and the new businessman pays(1?q1(t))Y(or(1?q2(t))Z).Let the reinsurance premium also be calculated by the expected value principle.For the new business,the premium has to be paid at rate(1?q1(t))(1+η1)(λ1+λ)μ1Y+(1?q2(t))(1+η2)(λ2+λ)μ1Z,η1and η2are the safety loadings of the reinsurer for the first class claims and second class claims,respectively.Without loss of generality,we assume that ηi> θi,i=1,2.Note that for the insurance company,qi(t)∈[0,1]corresponds to a reinsurance cover and qi(t)>1 would mean that the company can take an extra insurance business from other companies for i=1,2.After reinsurance,the premium of the insurer is equal to

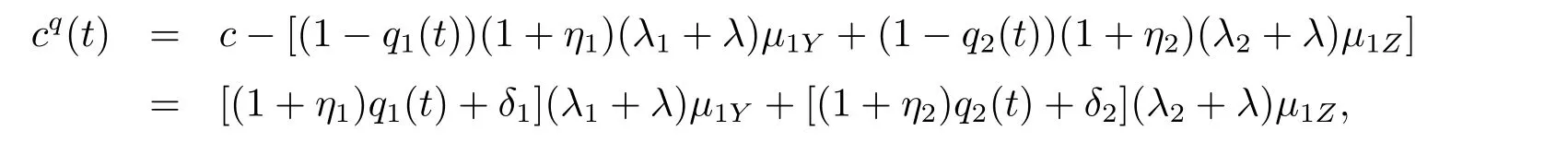
where δ1= θ1? η1,δ2= θ2? η2.Then the surplus process of the insurer is

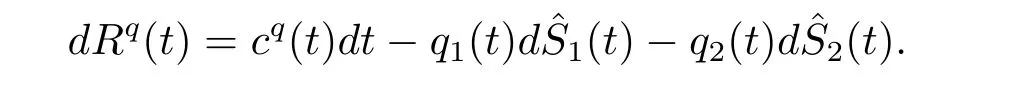
Suppose that a financial market consist of a risk-free asset(bond)and a risky asset(stock).The price process of the risk-free asset is modeled by

where r0(t)>0 is the interest rate of the risk-free asset.The price of the risky asset satisfies the following stochastic differential equation

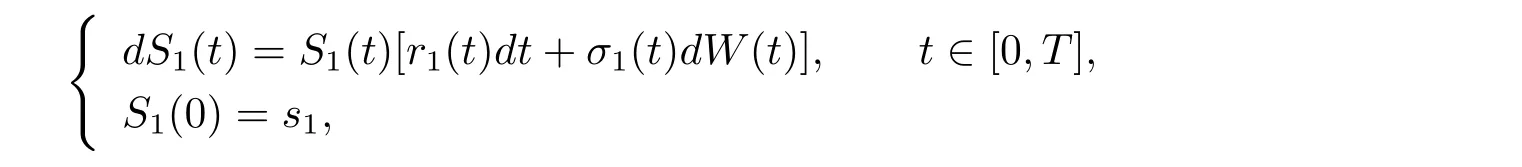
where r1(t)(>r0(t))is the appreciation rate and σ1(t)is the volatility coefficient;{W(t)}is a one-dimensional standard Brownian motion,which is independent of N1(t),N2(t),N(t),Yiand Zi.We assume that r0(t),r1(t)and σ1(t)are continuous bounded deterministic functions on[0,T].

Let X(t)denote the insurer’s wealth at time t.A trading strategy is denoted by π ={(q1(t),q2(t),β(t))}t∈[0,t],where β(t)is the dollar amount invested in the risky asset at time t.The dollar amount invested in the risk-free asset at time t is Xπ(t)? β(t),where Xπ(t)is the wealth process associated with strategy π.Then the surplus process Xπ(t)can be described as

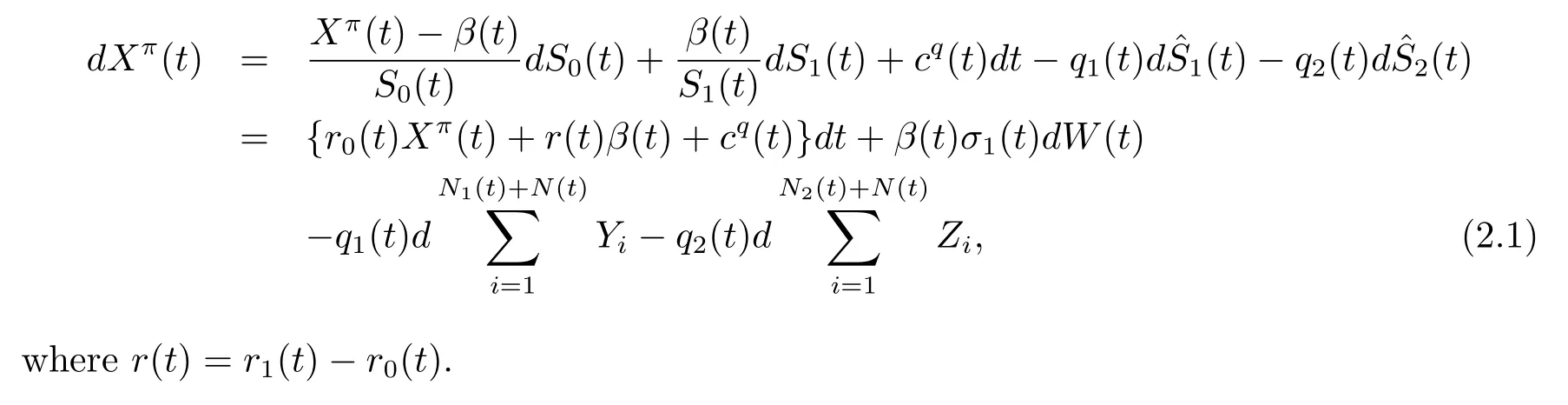
Definition 2.1(Admissible strategy)For any fixed t∈ [0,T],a strategy π ={(q1(s),q2(s),β(s))}s∈[t,T]is said to be admissible if it satisfies that

(i)(q1(s),q2(s),β(s))is Fs-predictable;

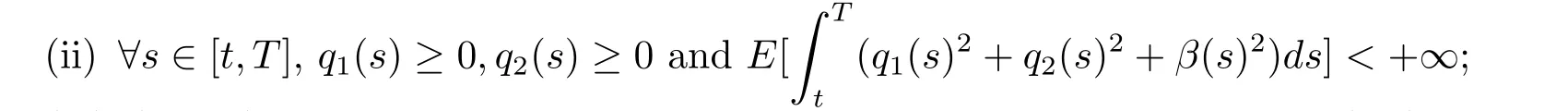
(iii)(π,Xπ)is the unique solution to the stochastic differential equation(2.1).

For any initial condition(t,x) ∈ [0,T]× R,let Π(t,x)denote the set of all admissible strategies.

3 Problem Formulation in A Game Theoretic Framework

In this section,we will formulate the problem within a game theoretic framework,which is developed by Bjork and Murgoci[11].We consider an optimization problem for the insurer to maximize the expected utility of the terminal wealth,where the utility function is of meanvariance form,that is,for any(t,x)∈ ([0,T]×R),the objective function which we want to maximize is given by

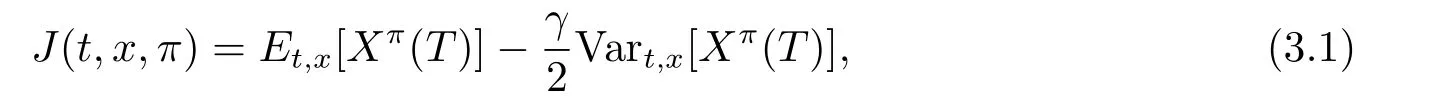
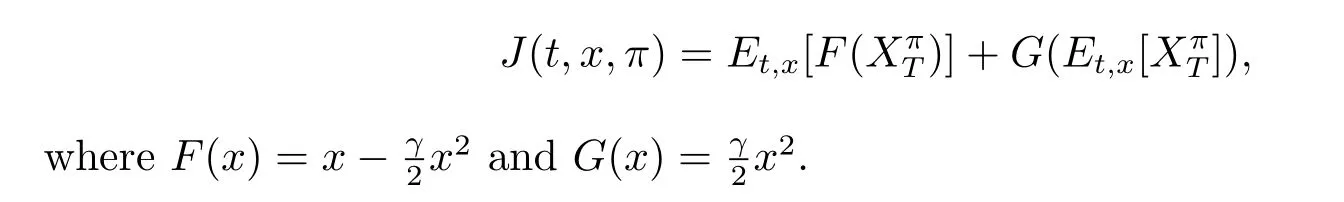
First,we present the following definition of an equilibrium control,which is from Bjork and Murgoci[11].

Definition 3.1(Equilibrium strategy)We say that an admissible strategy π?is an equilibrium strategy if for all given π∈R+×R+×R,h>0 and(t,x)∈[0,T]×R,

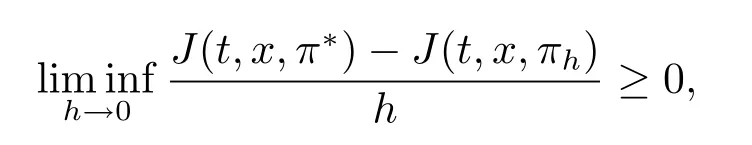
where πhis denoted by

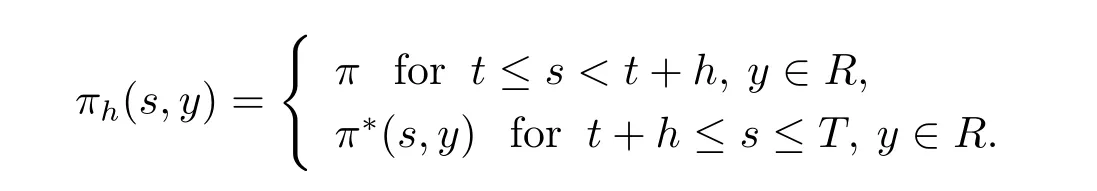
The corresponding equilibrium value function V(t,x)is defined by

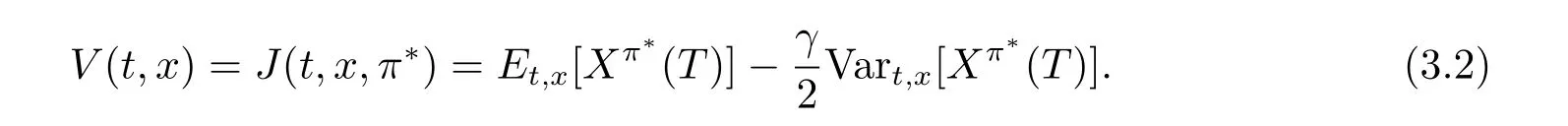
Based on the definition above,the equilibrium strategy is time-consistent and hereafter we call the equilibrium strategy and the corresponding equilibrium value function the optimal time-consistent strategy and the optimal value function for problem(3.1),respectively.

Therefore,we assume that the aim of the insurers is to find an equilibrium strategy and the corresponding equilibrium value function.

Let C1,2([0,T]× R)denote the space of φ(t,x)and its derivatives φt(t,x), φx(t,x),φxx(t,x)are continuous on[0,T]× R.For any function φ(t,x) ∈ C1,2([0,T]× R)and any fixed π ∈ Π,the usual infinitesimal generator Aπ,which is described in Bjork and Murgoci[11],for the jump-diffusion process(2.1)is defined by

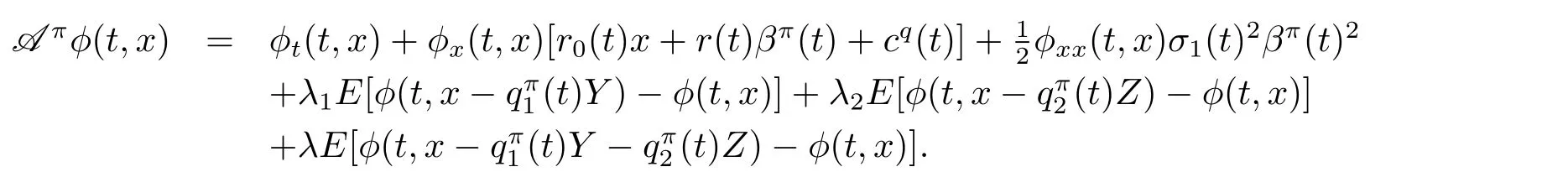
Then,we obtain the following extended Hamilton-Jacobi-Bellman system and the verification theorem.

Theorem 3.2(Verification theorem)For the optimization problem(3.1),if there exist two real value functions U(t,x),g(t,x)∈ C1,2([0,T]×R)satisfying the following extended HJB system:?(t,x)∈ [0,T]×R,

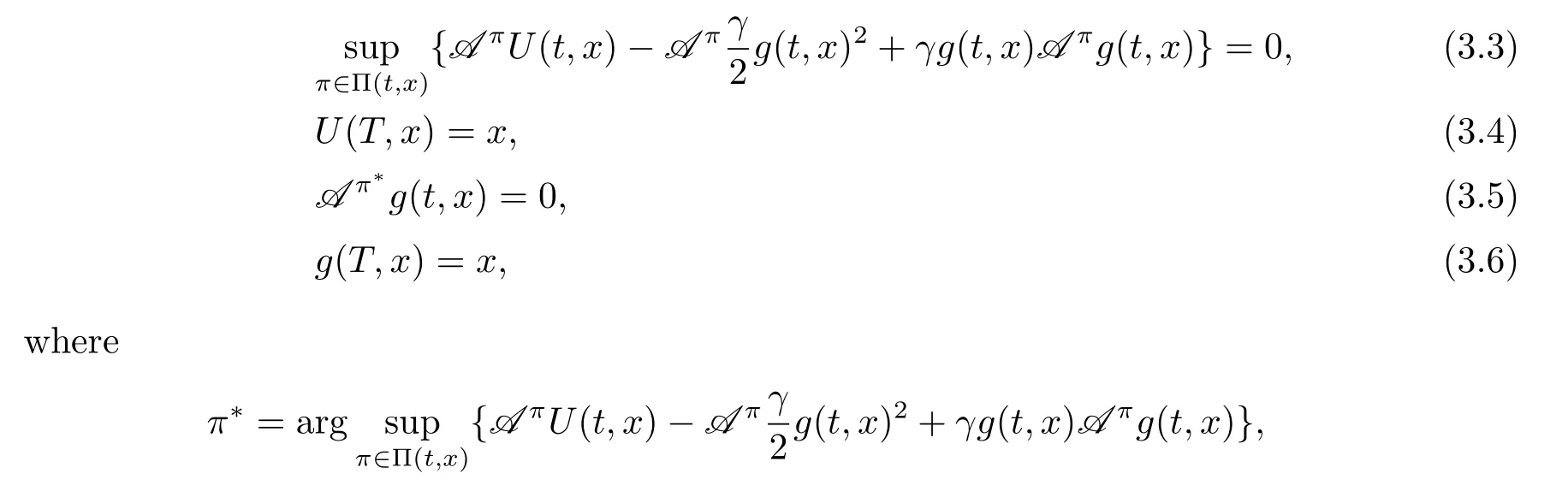
then V(t,x)=U(t,x),Et,x[Xπ?]=g(t,x),and π?is the optimal time-consistent strategy.

The proof of this theorem is similar to Theorem 4.1 of Bjork and Murgoci[11].

4 Solution to the Optimization Problem

In this section,we solve the investment-reinsurance optimization problem under the mean-variance criterion.

Suppose that there exist two functions U(t,x)and g(t,x)satisfying the condition given in Theorem 3.2.After elementary calculation,the following result is given

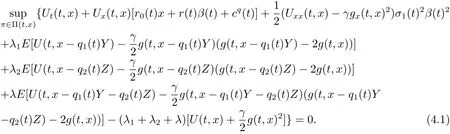
In the following,we aim to solve the optimization problem for the mean-variance criterion.Given the linear structure of(3.5)and(4.1),as well as the boundary conditions,it is natural to guess that

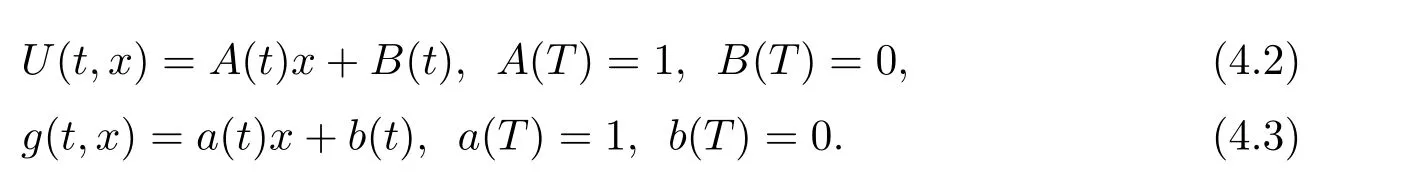
The corresponding partial derivatives are

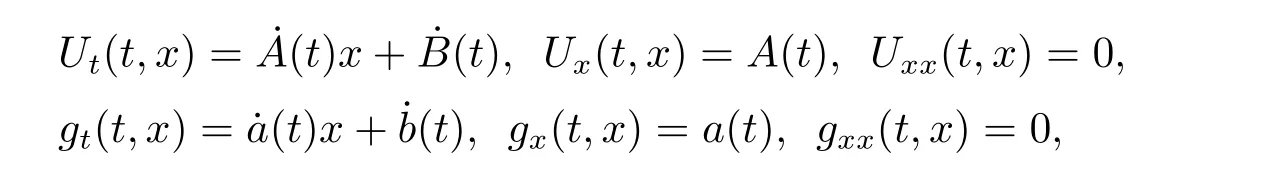
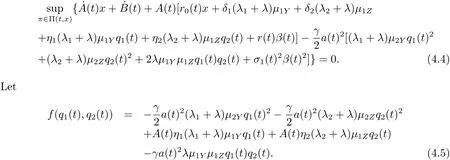
Differentiating the function h with respect to q1(t)and q2(t),respectively,we obtain

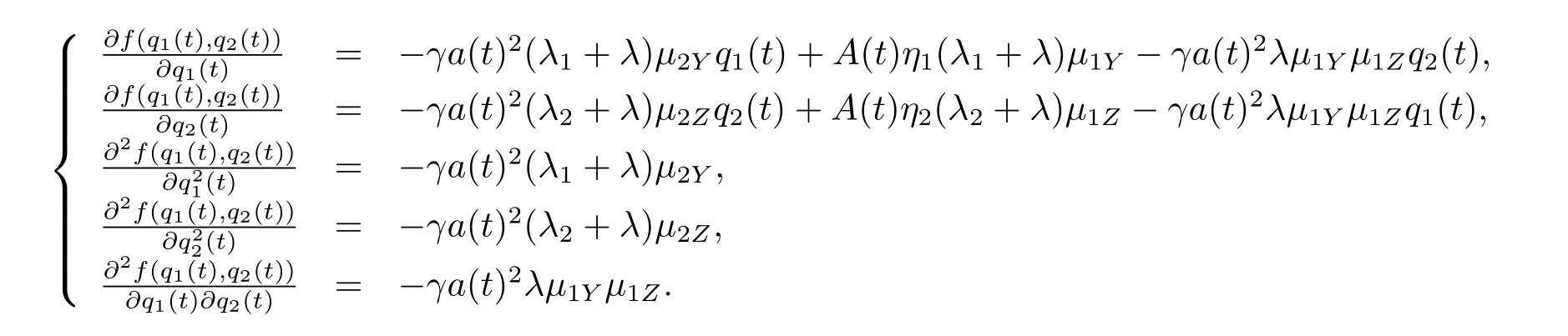
Then,the Hessian matrix is

it is easy to see that without restrictions q1(t)≥ 0 and q2(t)≥ 0,the maximizeris the solution of the equations

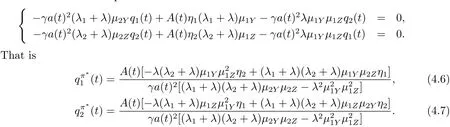
We assume that A(t)>0 initially,which is obviously true once we obtain the explicit expression of A(t)(see(4.11)).Because of the constraints of q1(t)≥0,q2(t)≥0 and the fact thatwe will discuss the following three cases.

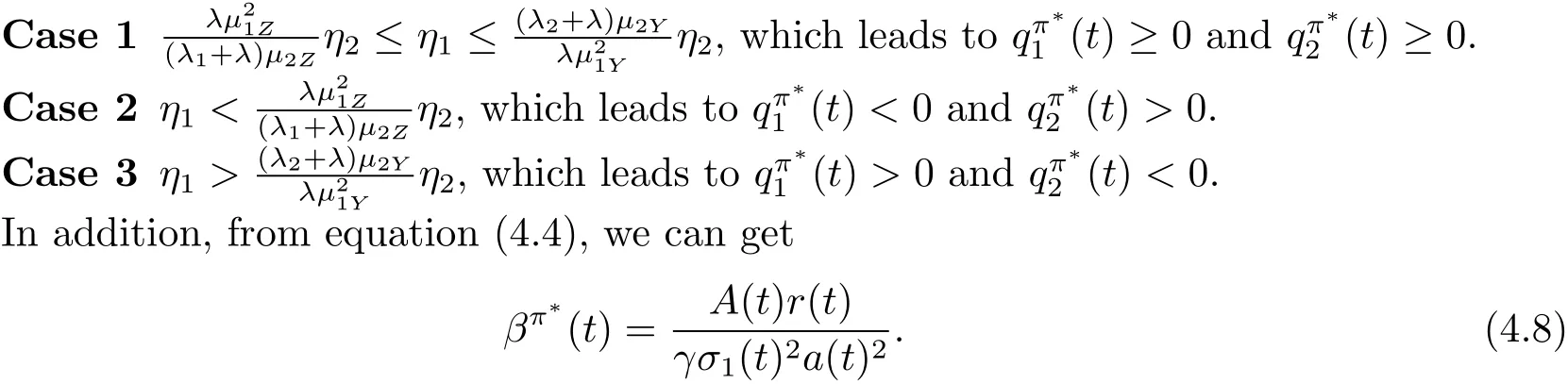
In the following,we only give the detailed discussion for Case 1.The results in Case 2 and Case 3 can be derived similarly.

Inserting(4.6),(4.7)and(4.8)into(4.4)and(3.5),we have

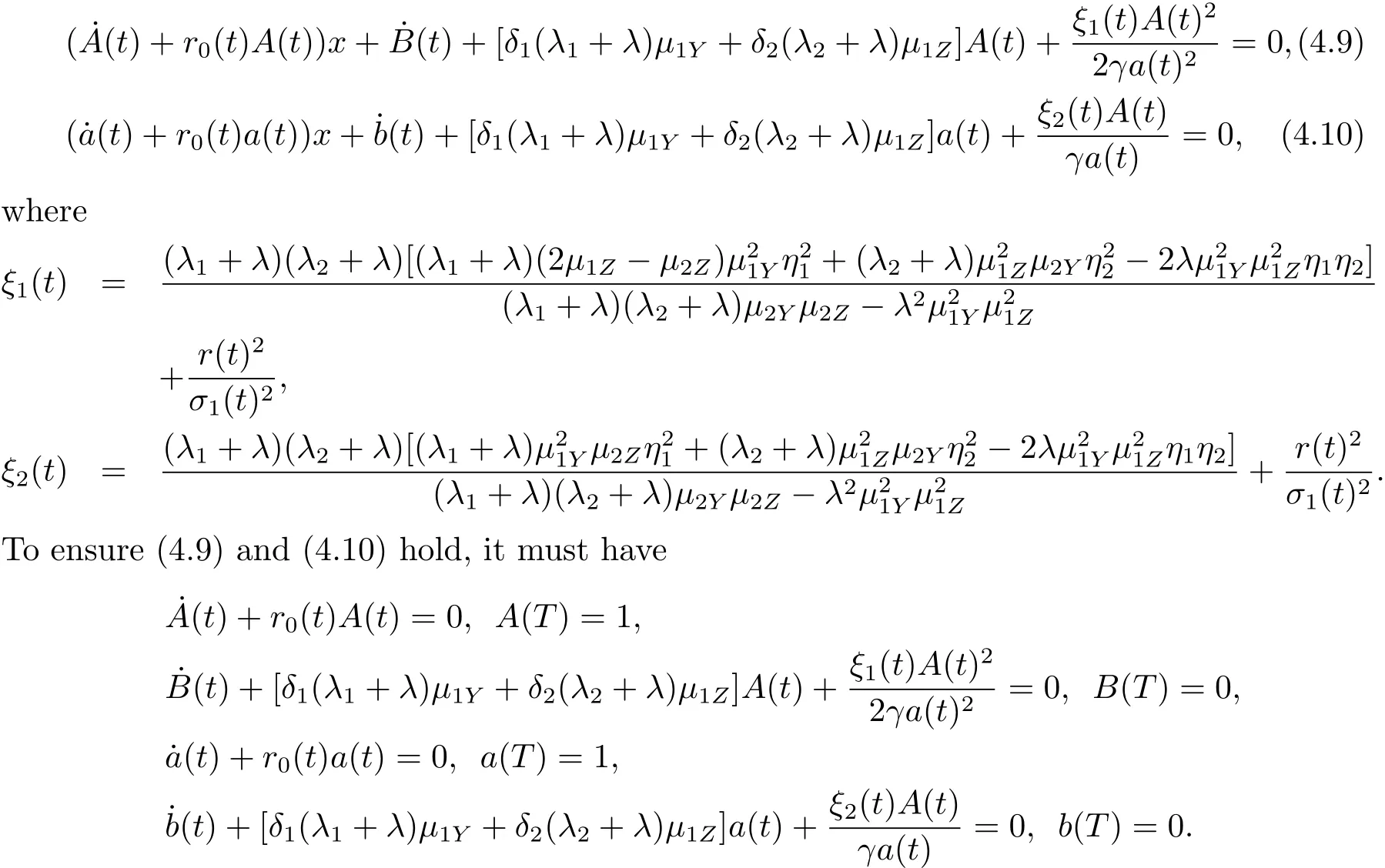
Solving the above equations,we obtain

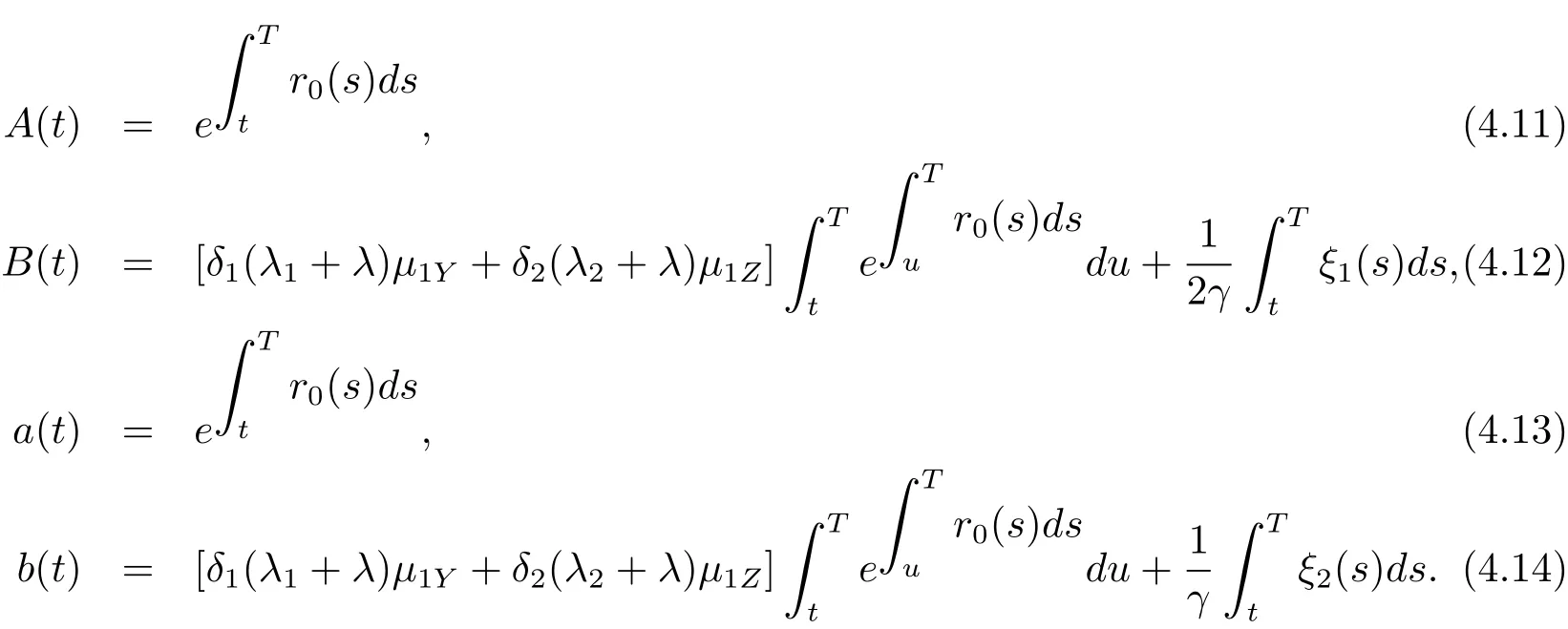
Substituting(4.11)and(4.13)into(4.6)–(4.8),we have

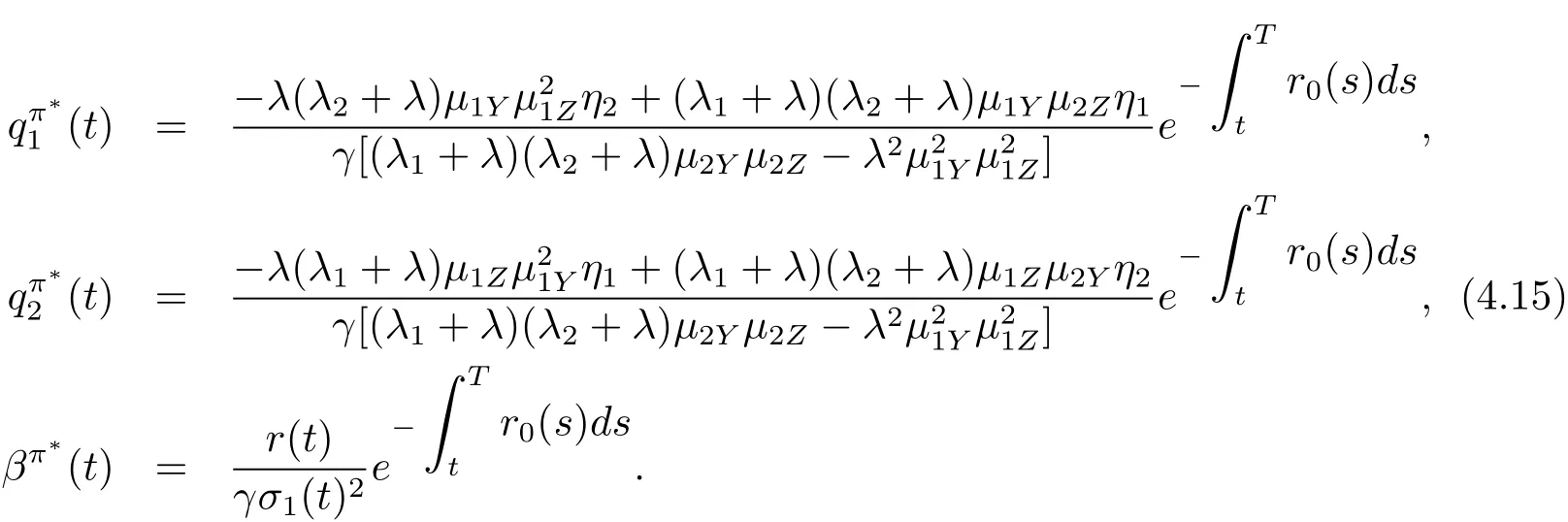
The above discussion leads to the following theorem.

Theorem 4.1 In Case 1,the optimal time-consistent strategy isand βπ?(t)are given by(4.15)and the optimal value function is given by

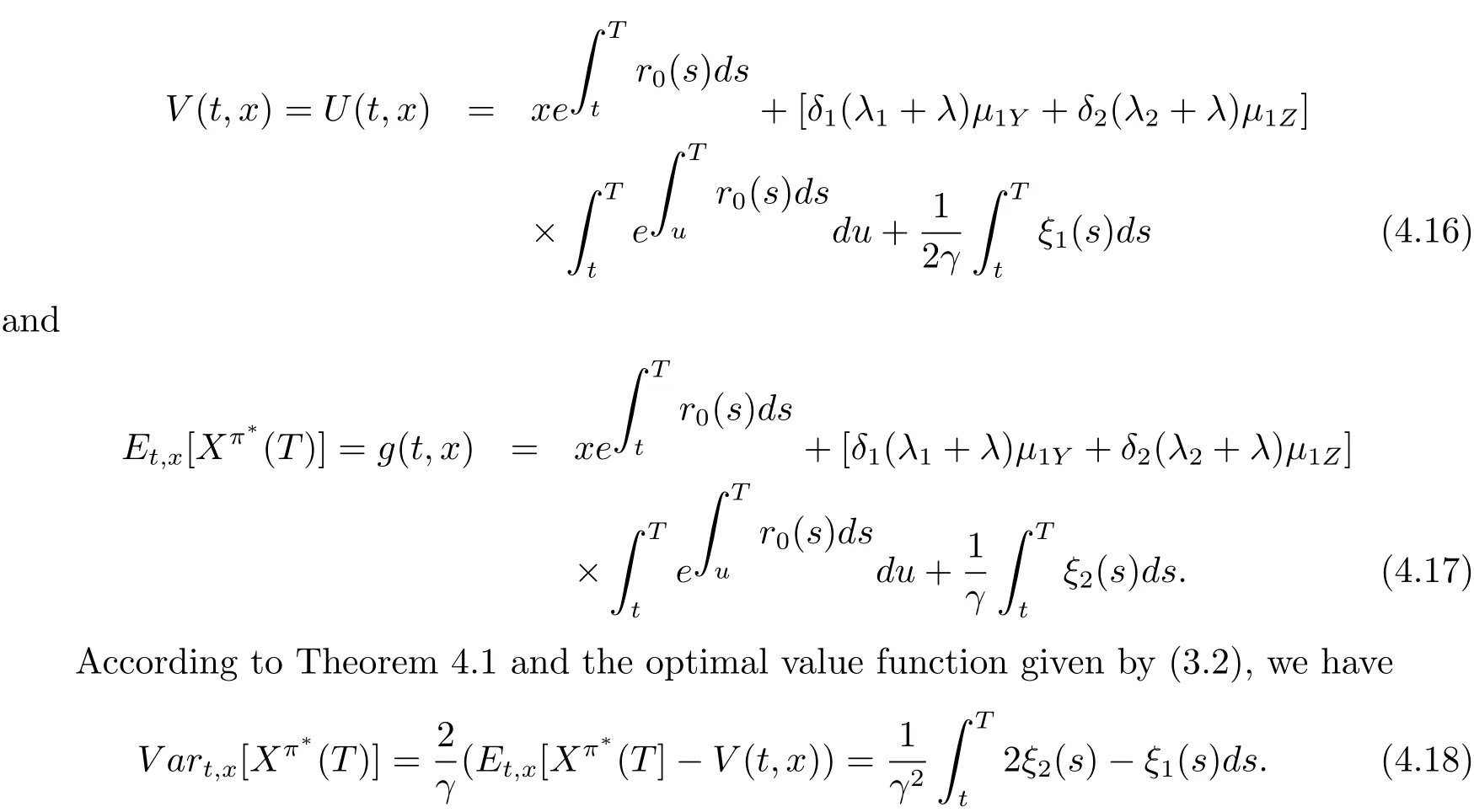
From(4.17)and(4.18),we can get the relationship between the expectation and the variance of the terminal wealth under the optimal strategy as below

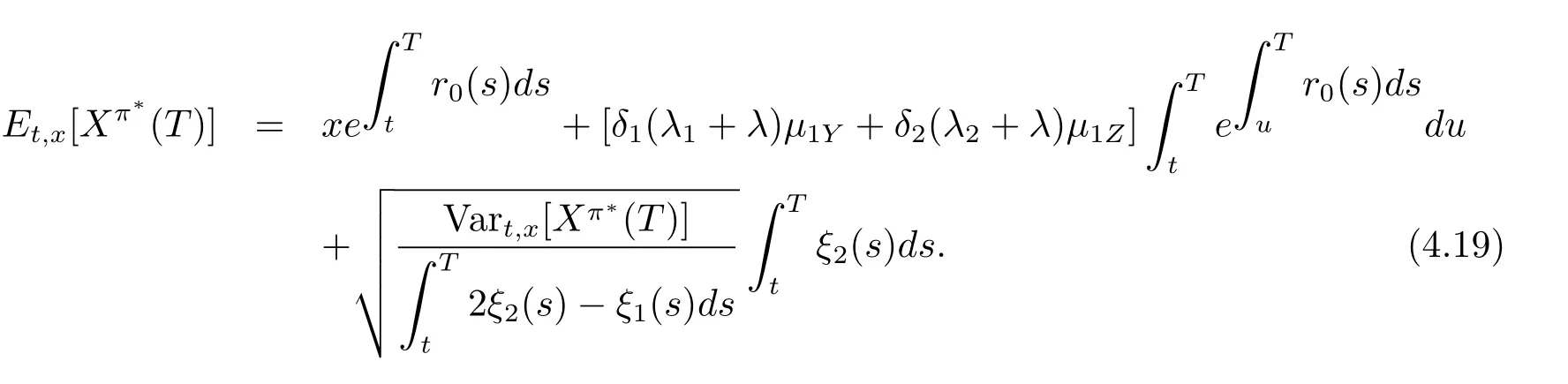
The relationship is known as the efficient frontier of problem(3.1)at initial state(t,x)in modern portfolio theory.In addition,by Theorem 4.1,we find that the optimal reinsurance strategy is independent of the parameters of the risky asset and the optimal investment strategy is independent of the parameters of the insurance business.

5 Numerical Illustration and Sensitivity Analysis

In this section,we provide some numerical examples to illustrate the effects of model parameters on the optimal time-consistent reinsurance-investment strategy.For convenience,but without loss of generality,we only analyze the results of the original model with r0(t)=r0,r1(t)=r1,σ1(t)= σ1for all t∈ [0,T].Throughout the numerical analyses,unless otherwise stated,the values of parameter are given as follows: λ =1,λ1=3,λ2=4,μ1Y=0.3,μ1Z=0.3,μ2Y=0.4,μ2Z=0.4,r0=0.06,r1=0.12,σ1=0.18,γ =0.5,θ1=0.2,θ2=0.2,η1=0.3,η2=0.3,T=10,t=0,x=1.

Some numerical illustrations and sensitivity analysis for the optimal time-consistent reinsurance strategy and the optimal time-consistent investment strategy are presented in this section.We only give the detailed analysis for the optimal time-consistent reinsurance strategy(t).The analysis result for q2π?(t)can be derived similarly.

Figure 1 shows that the optimal time-consistent reinsurance strategy q1π?(t)increases with respect to time t,namely,as time elapses,the insurer should keep more insurance business by purchasing less reinsurance or acquire more new business.In addition,subgraphs(a)and(b)illustrate that when the coefficient of the insurer’s risk aversion γ or intensity parameter λ increases,the insurer will purchase more reinsurance or acquire less new business.Subgraph(c)illustrates that when the intensity of the claims for the first class insurance business λ1increases,the insurer will purchase less reinsurance or acquire more new business.Subgraph(d)illustrates that the intensity of the claims for the second class insurance business λ2has a very little impact on the optimal time-consistent reinsurance strategy(t).

Figure 2 shows that the optimal time-consistent investment strategy βπ?(t)increase with respect to time t.Further,the optimal time-consistent investment strategy is decreasing while γ increases.It is reasonable because a large value of γ means more risk averse and the insurer will invest less money to the risky asset.

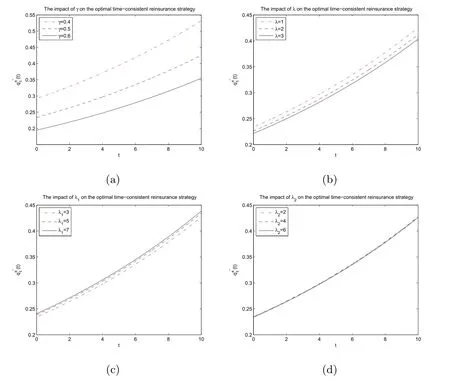
Figure 1:The impact of parameters on the optimal time-consistent reinsurance strategy

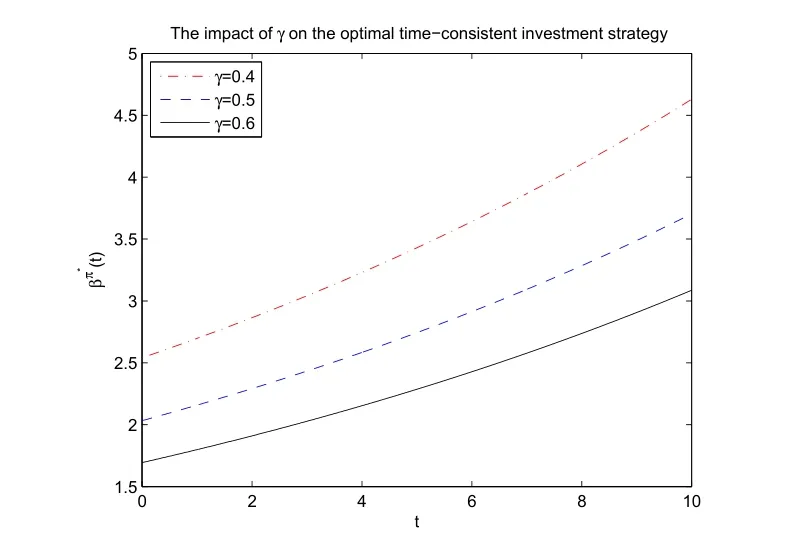
Figure 2:The impact of parameters on the optimal time-consistent investment strategy

6 Conclusion

We have studied the mean-variance optimal investment-reinsurance problem in a risk model with two dependent classes of insurance business,where the two claim number processes are correlated through a common shock component.Since the dynamic mean-variance problem is time-inconsistent,we tackle the problem from a game theoretic perspective.By adopting the approach developed in by Bjork and Murgoci[11],we obtain the optimal time consistent investment-reinsurance strategies and the corresponding optimal value function.Finally,the effects of parameters on the optimal time-consistent strategies are presented.In future research,it would be interesting to extend our analysis to some more general situations,such as adopting a wealth-dependent risk aversion coefficient and using a jump diffusion process or more general Levy process for the risky asset price process.Of course,these problems are more complicated.To solve such problems,we need to adopt much more sophisticated techniques.