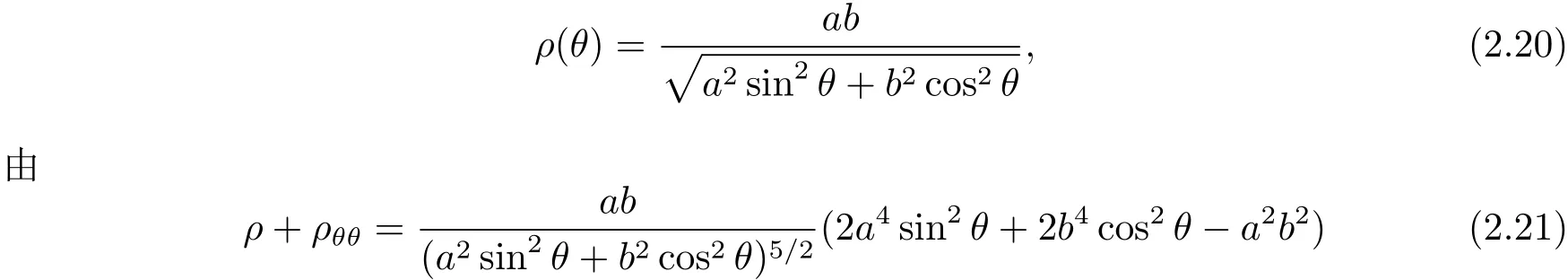鄭高峰,周 陽

(華中師范大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)學(xué)院,湖北武漢 430079)

1 引言

經(jīng)典等周不等式:對平面內(nèi)任一條簡單閉曲線γ,設(shè)其周長為L,所圍區(qū)域面積為A,有

等號成立當(dāng)且僅當(dāng)γ是一個圓周.

1882年,Edler第一個給出嚴(yán)格的數(shù)學(xué)證明,此后相繼出現(xiàn)多種不同證明方法[3],而在這些證明中,用到極坐標(biāo)的情況非常少,不等式中帶有極坐標(biāo)形式的基本沒有.因此給出一些帶有極坐標(biāo)形式的等周型不等式是必要的.并且從文中定理2.4,定理2.5中帶有極坐標(biāo)的等周型不等式來看,當(dāng)L2?4πA=0時,可以很直觀的發(fā)現(xiàn)該曲線為圓周.

2 主要結(jié)果及其證明

引理2.1[4]對任意一條簡單閉曲線γ,存在唯一一個包含γ的最小圓環(huán).并且至少存在四點P1,P2,P3,P4,其中P1,P3在該圓環(huán)的內(nèi)圓周上,P2,P4在該圓環(huán)的外圓周上,使得P1,P2,P3,P4依次排列在曲線γ上.

注 Chouikha[5]對Jordan多項式的情形作出了證明,在文獻(xiàn)[4]中推廣到一般簡單閉曲線.

接下來,如無特別說明,我們一直假設(shè)γ是一條C2可求長的正定向閉凸曲線,設(shè)其周長為L,所圍區(qū)域面積為A.由引理2.1,存在唯一一個包含γ的最小圓環(huán),記其中心為O,其內(nèi)外圓周的半徑分別為rin(O),rout(O).以O(shè)為坐標(biāo)原點,任選一方向為極軸方向,建立極坐標(biāo)系 {O;ρ(θ)}.

引理2.2[2]如果O是包含閉凸曲線γ的最小圓環(huán)的中心,則γ的Bonnesen函數(shù)

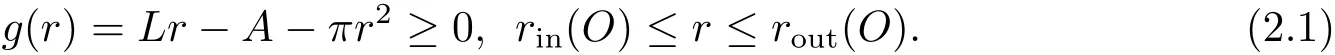
注 Bonnesen[1]在1921年提出了Bonnesen不等式,由文獻(xiàn)[2]中(1.7)式可以得到此引理.

定理2.3 若ρ(θ)是按上述定義在C2閉凸曲線γ上的極坐標(biāo),則有

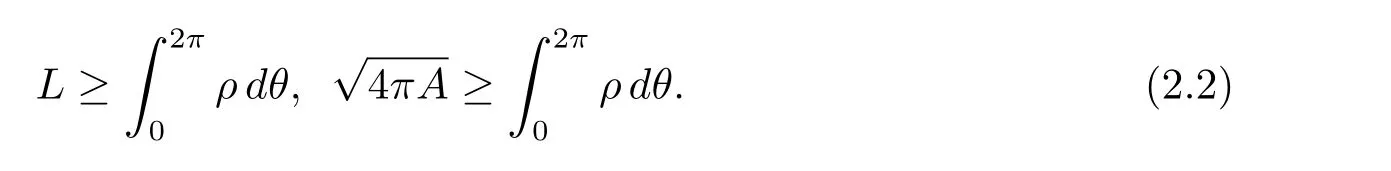
并且兩個不等式取等皆當(dāng)且僅當(dāng)γ為圓周.

證

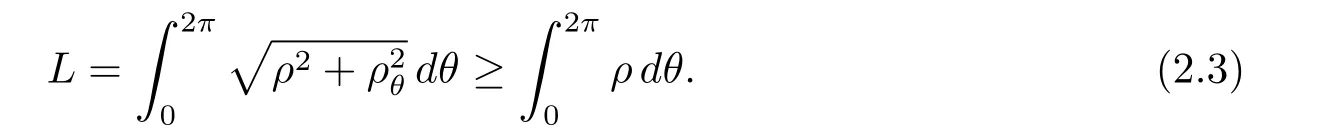
由于

再運用Cauchy不等式

定理2.4 若ρ(θ)是按上述定義在C2閉凸曲線γ上的極坐標(biāo),則有

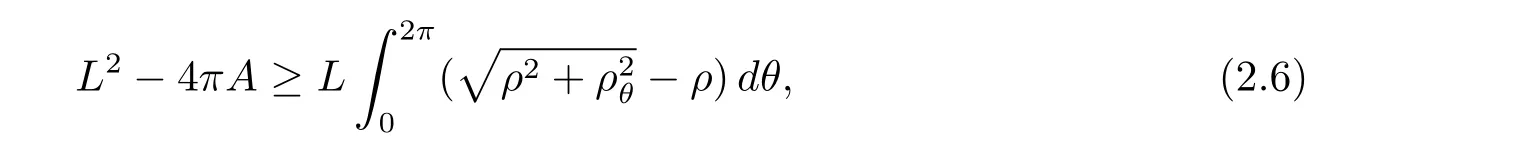
并且該不等式取等當(dāng)且僅當(dāng)γ為圓周.

證 由于{O;ρ(θ)}是以包含γ的最小圓環(huán)的中心為原點,故

因此由引理2.2,

由此可得(2.6)式.

若γ為圓周,則ρ(θ)≡ 0,(2.6)式兩邊恒為0,故取等.反過來,若(2.6)式取等,則(2.9)式取等,由(2.8)式左邊函數(shù)的連續(xù)性可知g(ρ)≡ 0,?ρ∈[rin(O),rout(O)],因此rin(O)=rout(O),故γ為圓周.

定理2.5 若ρ(θ)是按上述定義在C2閉凸曲線γ上的極坐標(biāo),則有

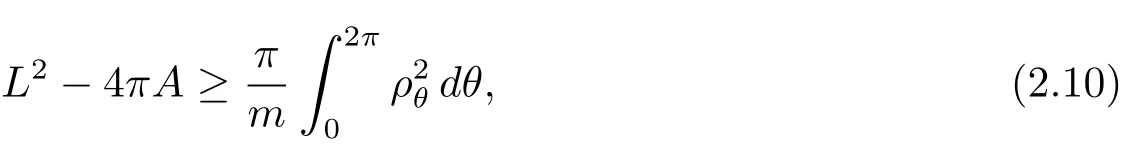
若

由于{O;ρ(θ)}是以包含γ的最小圓環(huán)的中心為原點,故

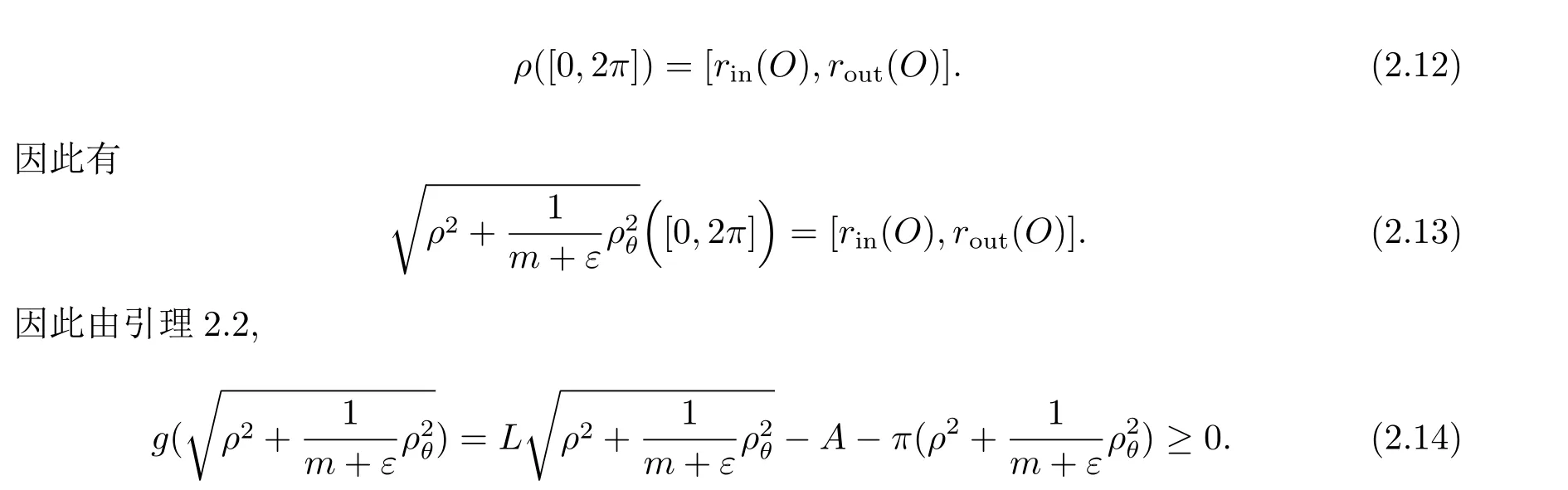
由ε的任意性可得(2.10)式.

若γ為圓周,則ρ(θ)≡ 0,則(2.10)式兩邊恒為0,故取等.反過來,若(2.10)式取等,則由被積函數(shù)的連續(xù)性,因此rin(O)=rout(O),故γ為圓周.

推論2.6 若ρ(θ)是按上述定義在C2閉凸曲線γ上的極坐標(biāo),k為曲線γ的曲率,且則有

并且其中兩個不等式取等皆當(dāng)且僅當(dāng)γ為圓周.

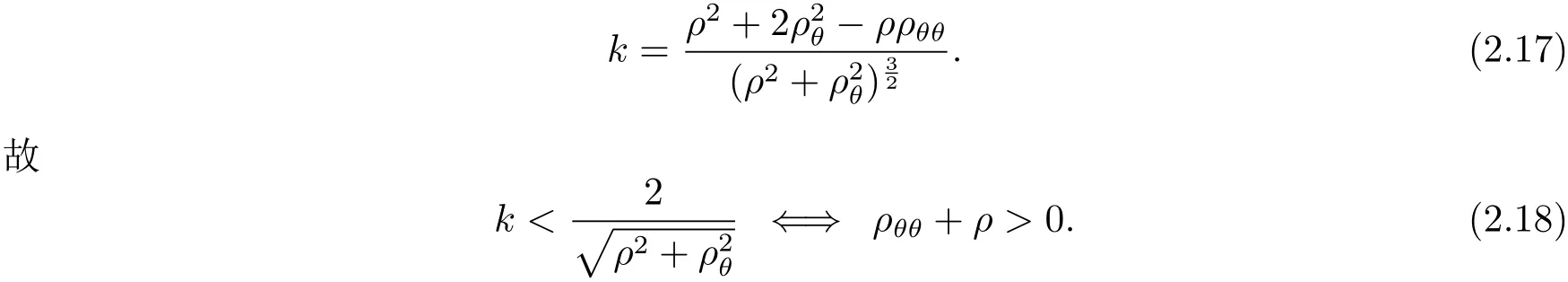
證 由于按照定理2.5的證明方法,可得(2.16)式左側(cè)不等式,至于后面的不等式,可由Cauchy不等式

事實上,由橢圓極坐標(biāo)形式