一類帶負(fù)交叉擴(kuò)散項(xiàng)的SIR傳染病模型的空間Turing斑圖
周 文,胡 偉,陳金瓊,凱 歌
(1.安徽師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,安徽蕪湖 241002)
(2.北京工業(yè)大學(xué)機(jī)電學(xué)院,北京 100124)
1 引言
根據(jù)世界衛(wèi)生組織的最新研究,傳染病依舊是人類死亡的第一殺手.由于對傳染病的研究不宜采用實(shí)驗(yàn)的形式,因此理論分析與數(shù)值模擬常被用于傳染病的機(jī)理研究上.此時(shí)選擇合適的傳染病的動力學(xué)模型顯得十分重要,常見的傳染病模型有SI,SIR,SEIR等等.
在傳染病的動力學(xué)研究中,許多學(xué)者做出有意義的結(jié)果,特別是傳染病模型的空間斑圖動力學(xué)[1?4].孫桂全,靳禎等人研究了一類帶有時(shí)滯的SIR空間傳染病模型的Turing失穩(wěn),通過數(shù)值模擬得出了條狀與點(diǎn)狀共存的斑圖[1].王瑋明等人研究了一類SI傳染病模型,通過推導(dǎo)模型的振幅方程做出斑圖選擇,得到了不同類型的Turing斑圖[2].馬知恩和周義倉在研究中提出了這樣的一個(gè)比例依賴型的模型[5]
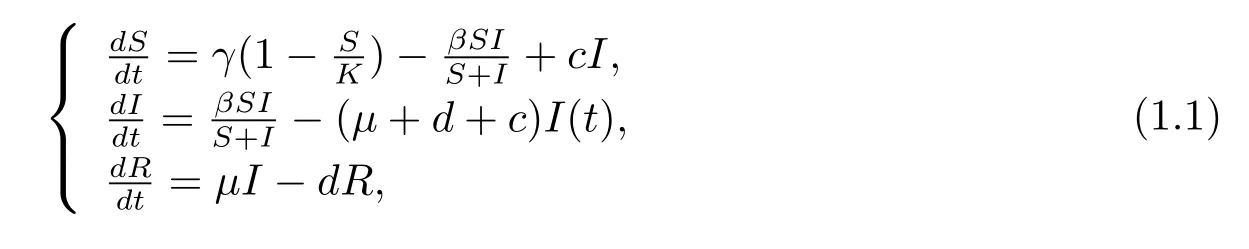
由于R與S,I無關(guān),所以作者利用穩(wěn)定性理論討論了下面一個(gè)微分方程組的平衡點(diǎn)的存在性與穩(wěn)定性
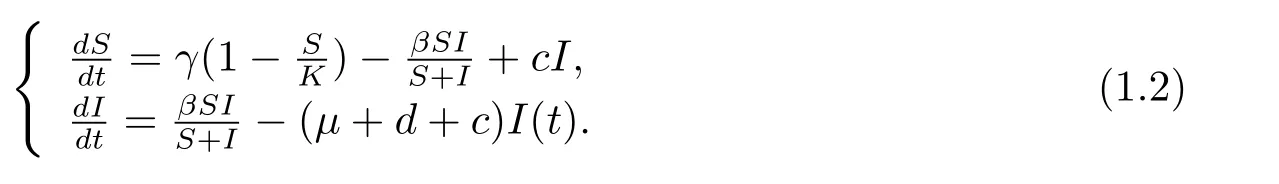
考慮到疾病對易感者與感染者心理上的影響,本文在此基礎(chǔ)上研究了一類帶有負(fù)交叉擴(kuò)散項(xiàng)的SI傳染病模型
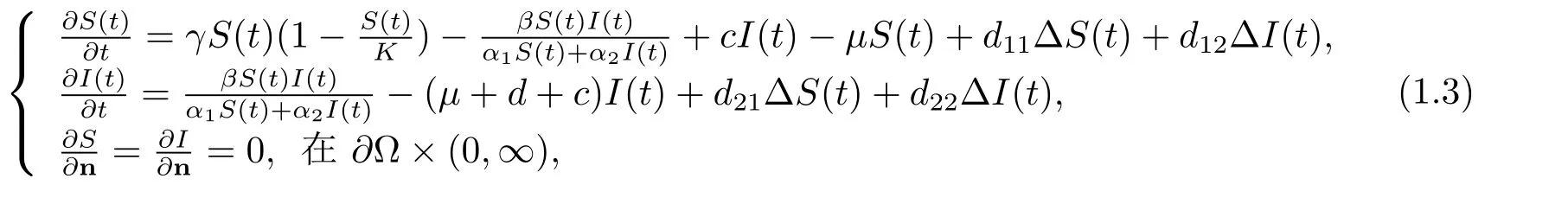
在這里S(t)和I(t)分別代表時(shí)間t時(shí)易感者和感染者的密度,γ和K分別代表了內(nèi)稟增長率和環(huán)境的承載力,μ代表人口的自然死亡率,d代表了因病死亡率,c代表了染病者的恢復(fù)率,β是傳染病系數(shù),是傳染率,α1和α2心理影響系數(shù),并且α1和α2都是常數(shù),?代表空間?中的Laplace算子,Neumann邊界條件表明模型(1.3)是自我封閉的,并且是零流量的,n代表著光滑邊界??上的單位外法向量.
這里需要指出的是,在之前的文獻(xiàn)[1–4]中,研究的傳染病模型所帶的交叉擴(kuò)散系數(shù)都是正數(shù),其生物學(xué)意義是人群總是從另一人群的高密度區(qū)域向低密度區(qū)域移動[6?7].而在實(shí)際生活中,人群從低密度區(qū)域向高密度區(qū)域移動的現(xiàn)象也是存在的.一方面,考慮到在生活中易感者有辨別染病者的能力并且會遠(yuǎn)離染病者,同時(shí)染病者也會遠(yuǎn)離易感者[6].另一方面,在疾病爆發(fā)初期,由于人們的心理因素,覺得人多的地方就是安全的地方,染病者反而會盡量接近易感者.所以在某種特定的情況下,這種染病者向易感者移動的現(xiàn)象在模型中則表現(xiàn)為交叉擴(kuò)散系數(shù)為負(fù)數(shù).據(jù)我們所知,帶有負(fù)交叉擴(kuò)散系數(shù)的傳染病模型的Turing斑圖在生物模型中很少被研究.因此本文將研究帶有負(fù)交叉擴(kuò)散系數(shù)的二維模型中的Turing斑圖的生成問題.
2 Turing空間的確定
首先考慮模型(1.3)
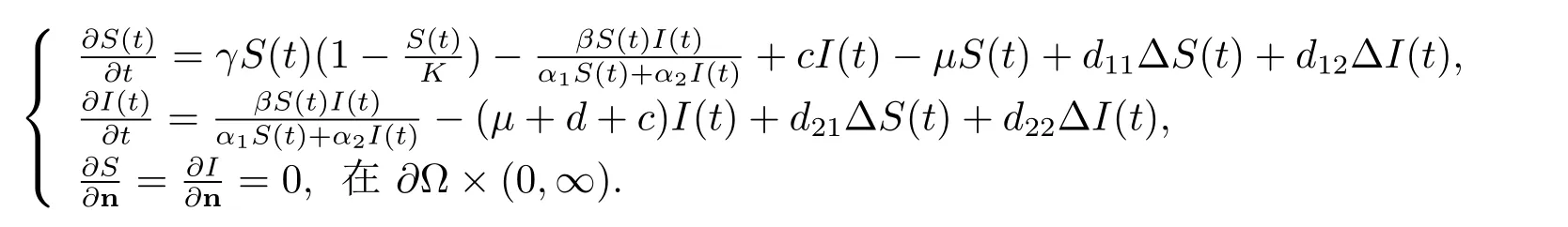
易知系統(tǒng)(1.3)有很多平衡點(diǎn),包括E0=(0,0),穩(wěn)定節(jié)點(diǎn)E1=(K(1?,0),和正平衡點(diǎn)E?=(S?,I?),從生物學(xué)上考慮,正平衡點(diǎn)更加有討論的意義,其中
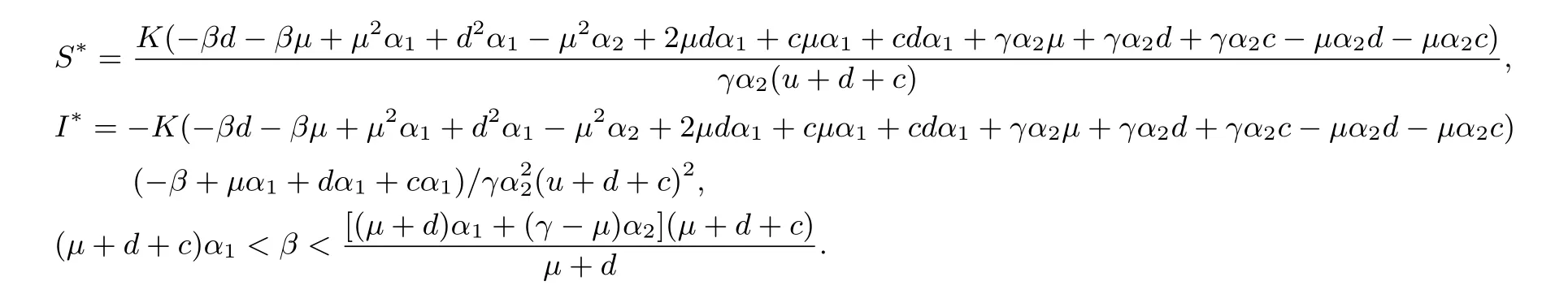
定理2.1不帶有擴(kuò)散項(xiàng)的系統(tǒng)(1.3)的平衡點(diǎn)(S?,I?)是局部漸近穩(wěn)定的.
證 為了討論方便,記
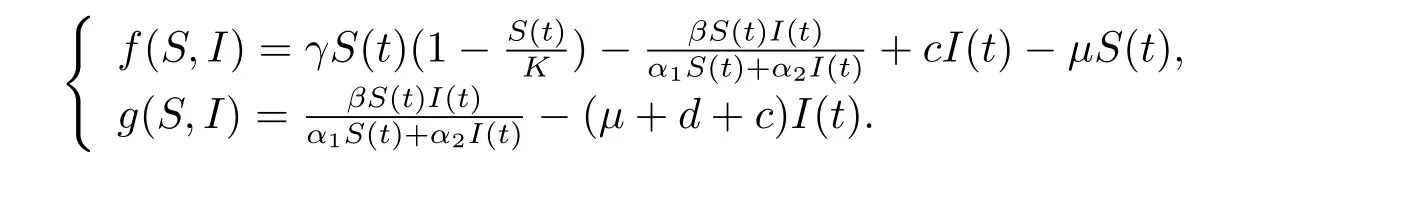
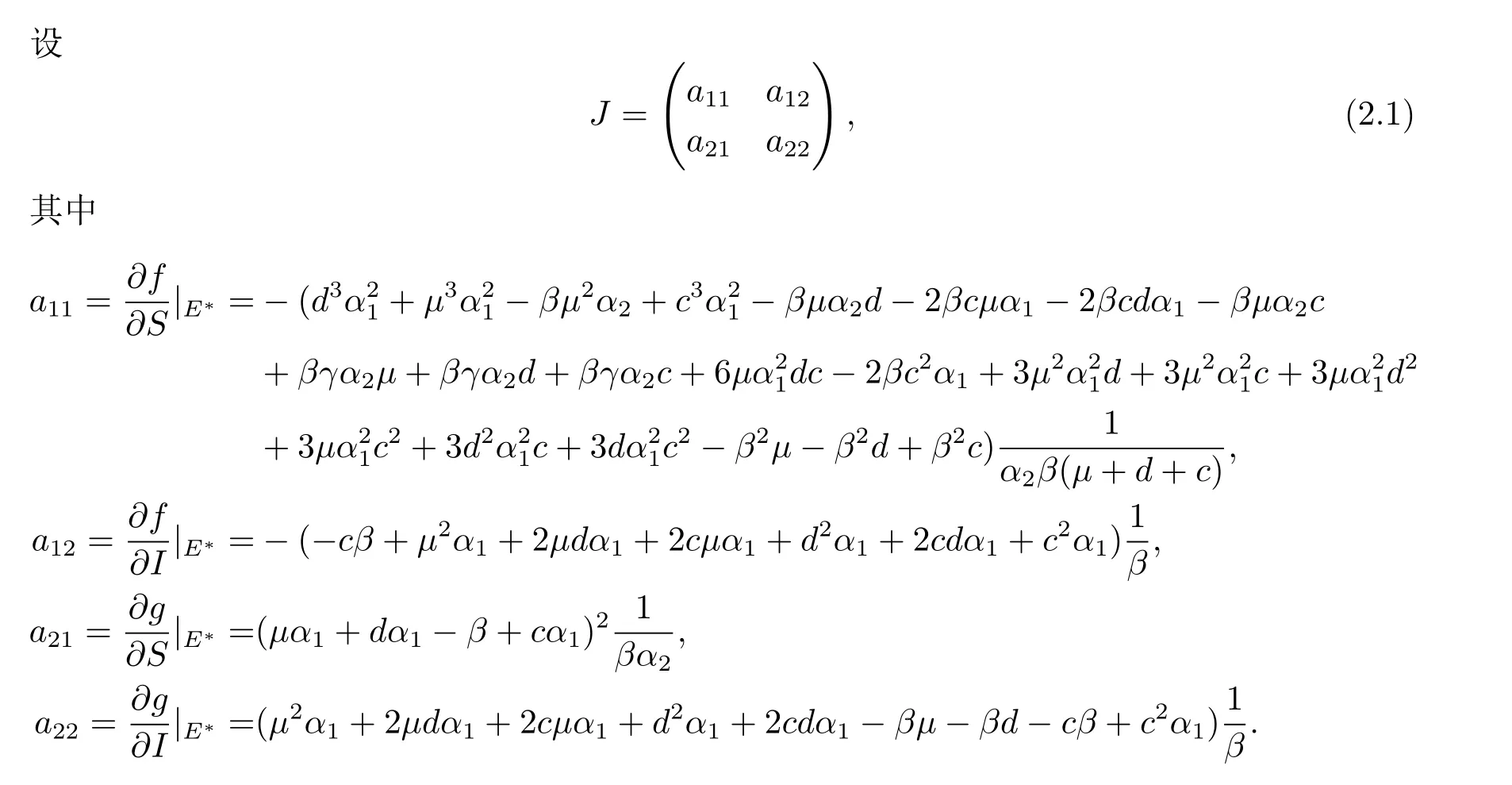
J的特征方程是
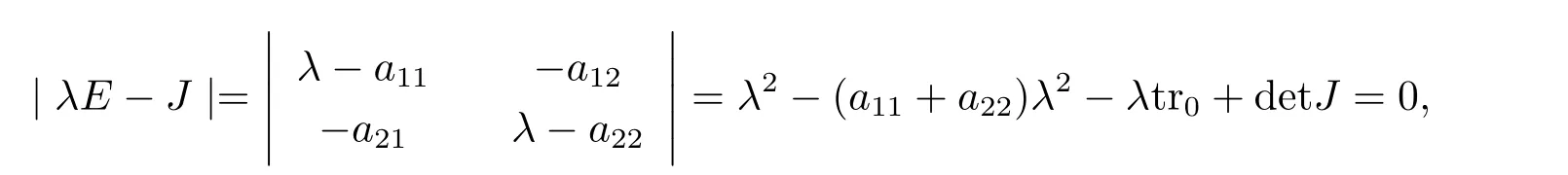
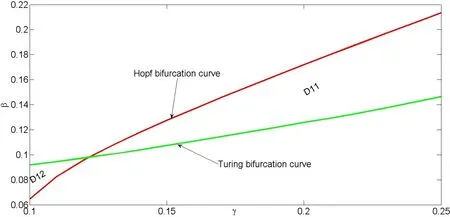
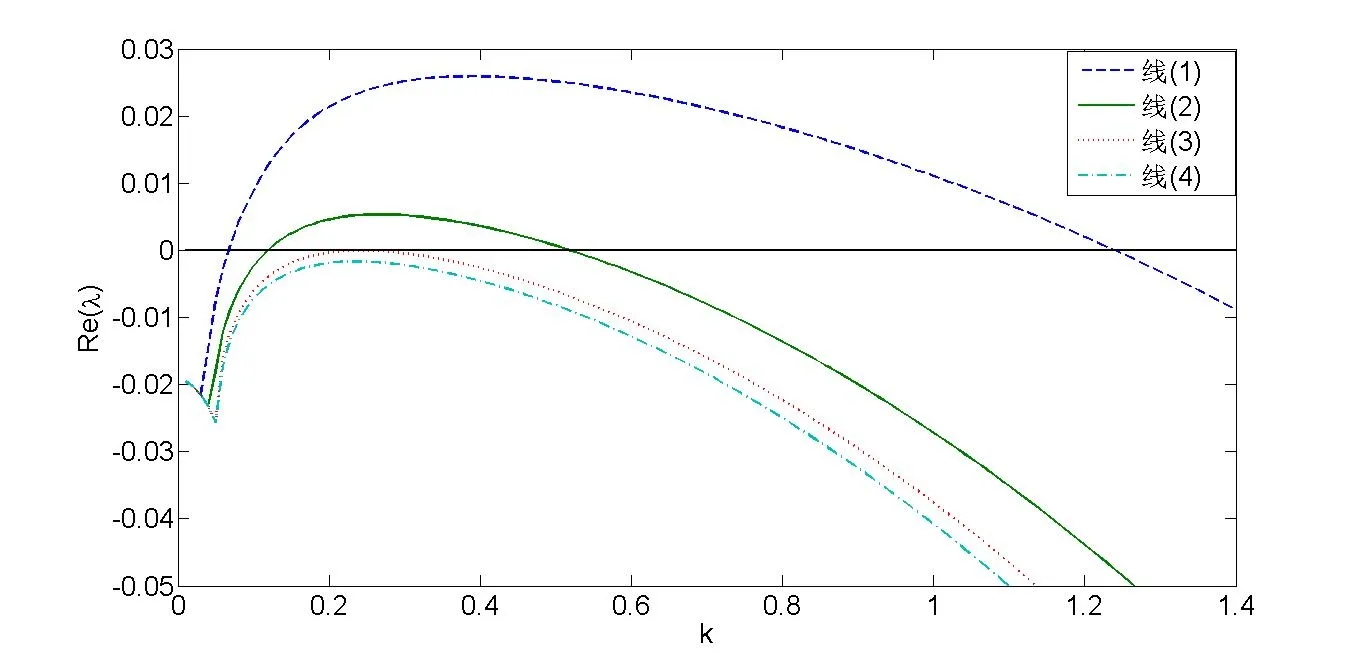
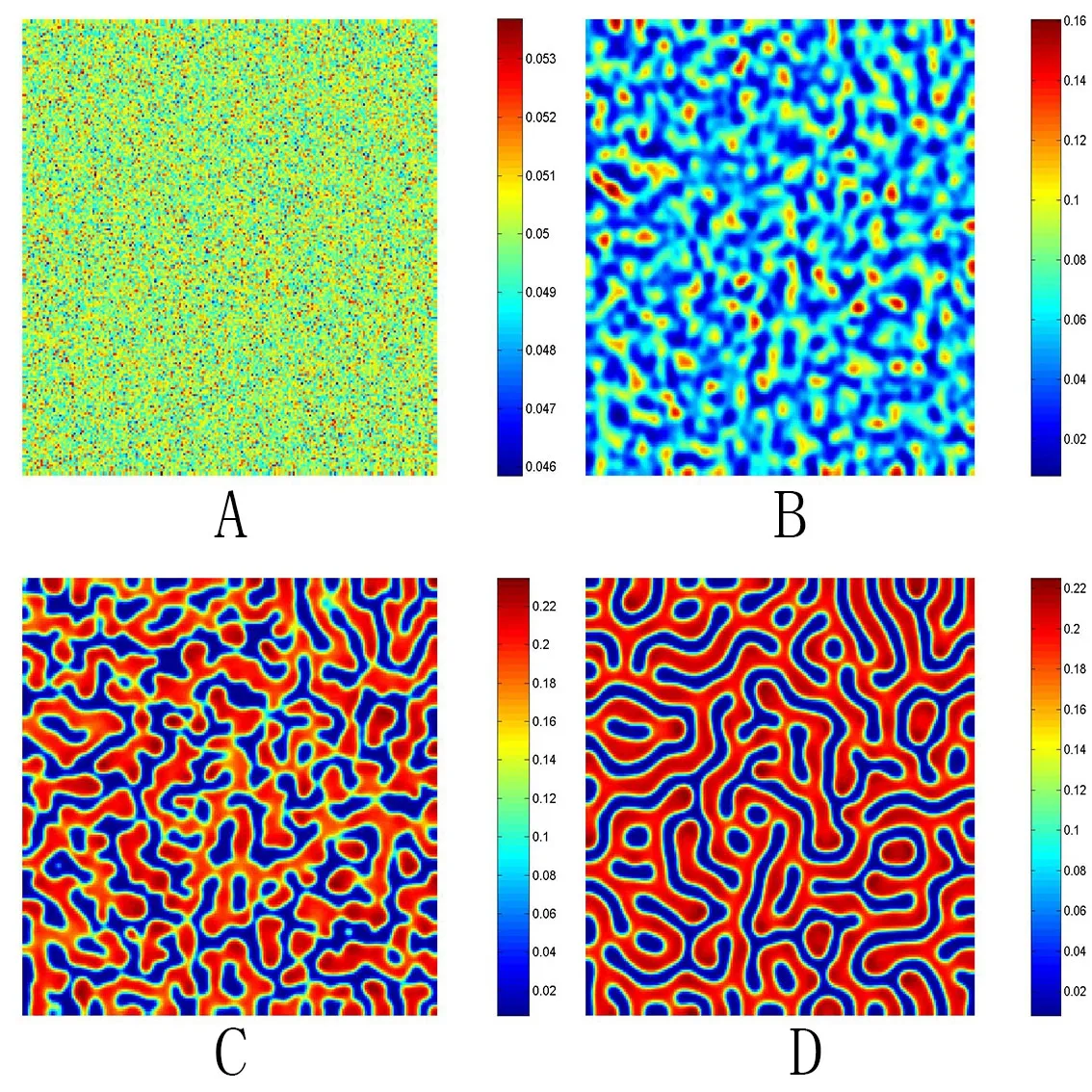
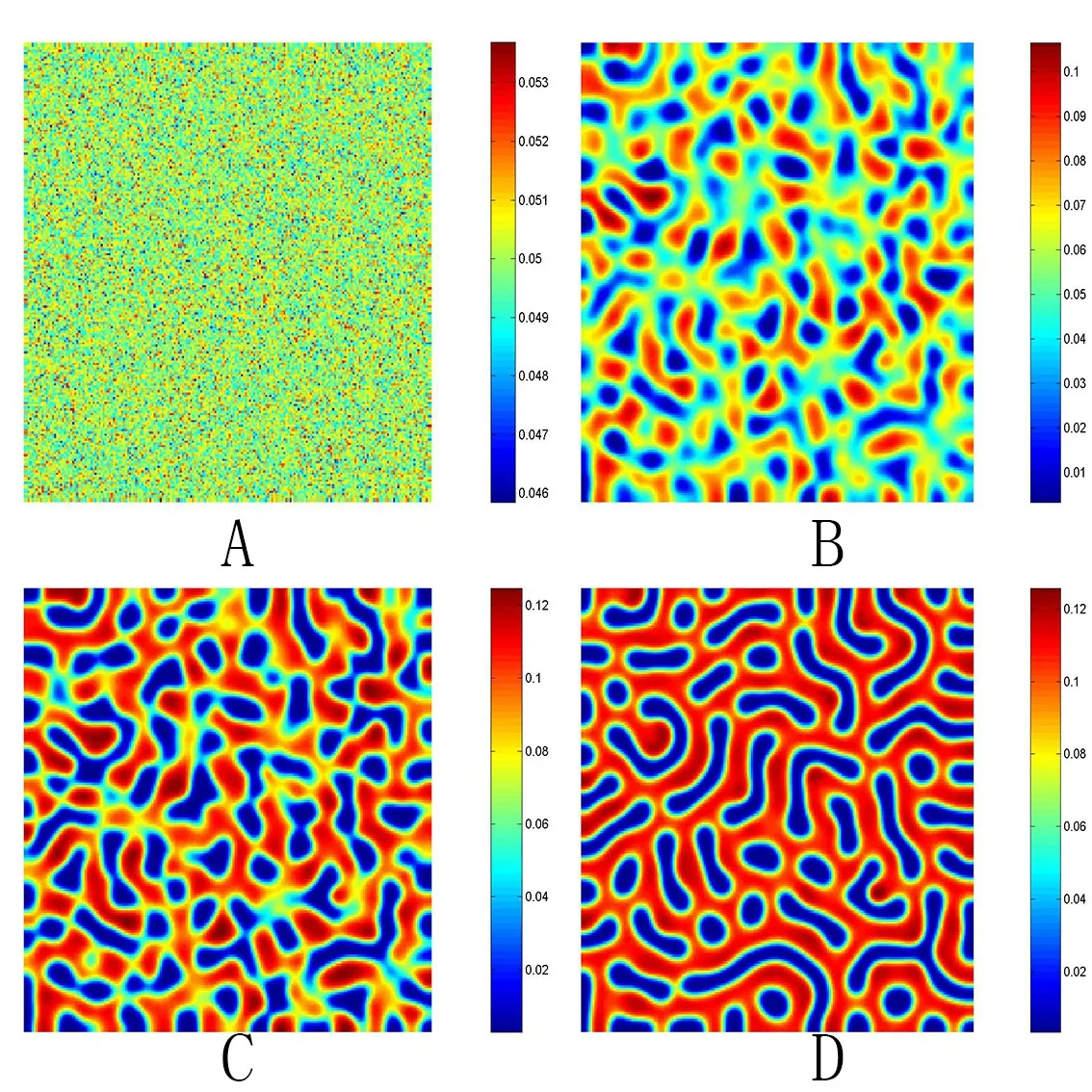
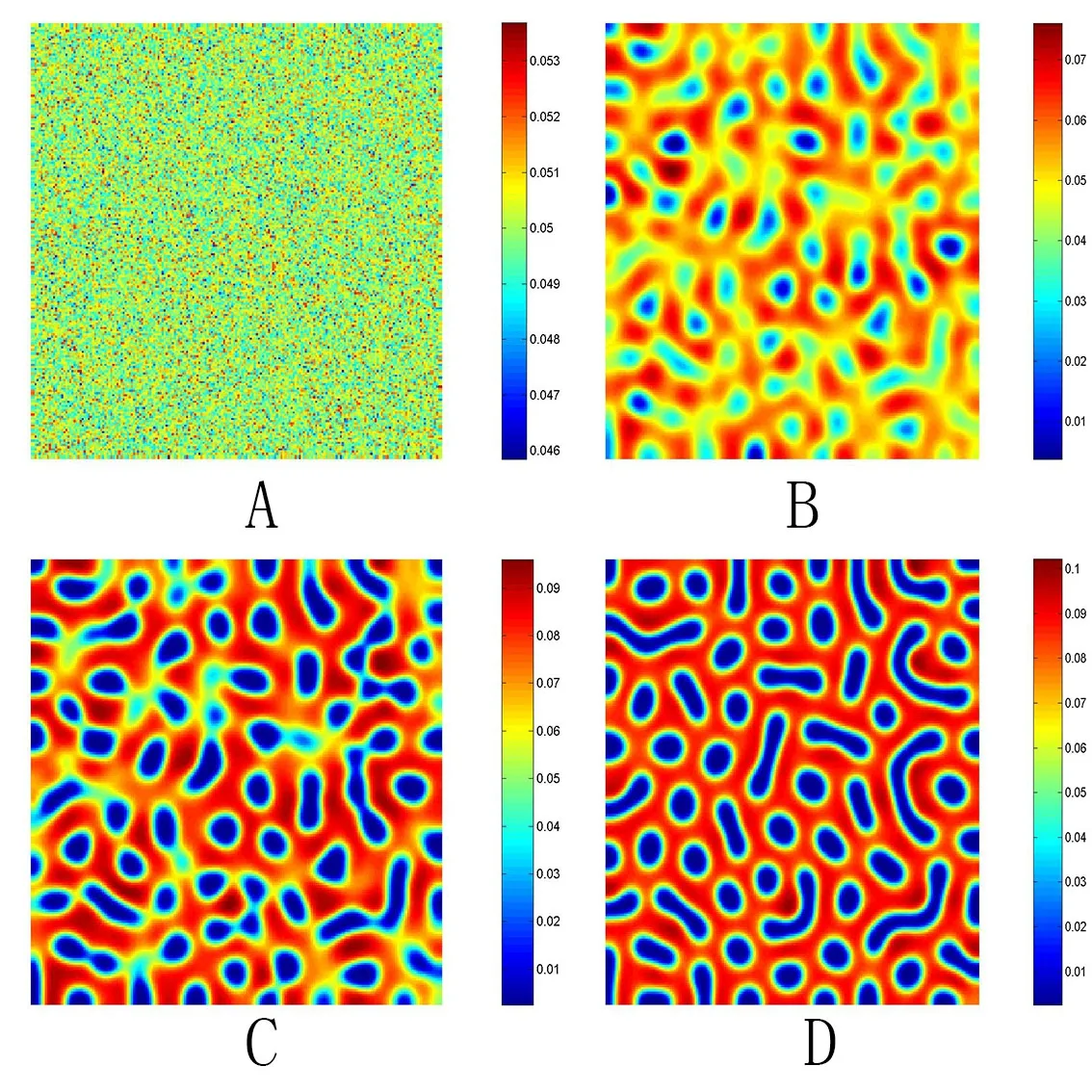
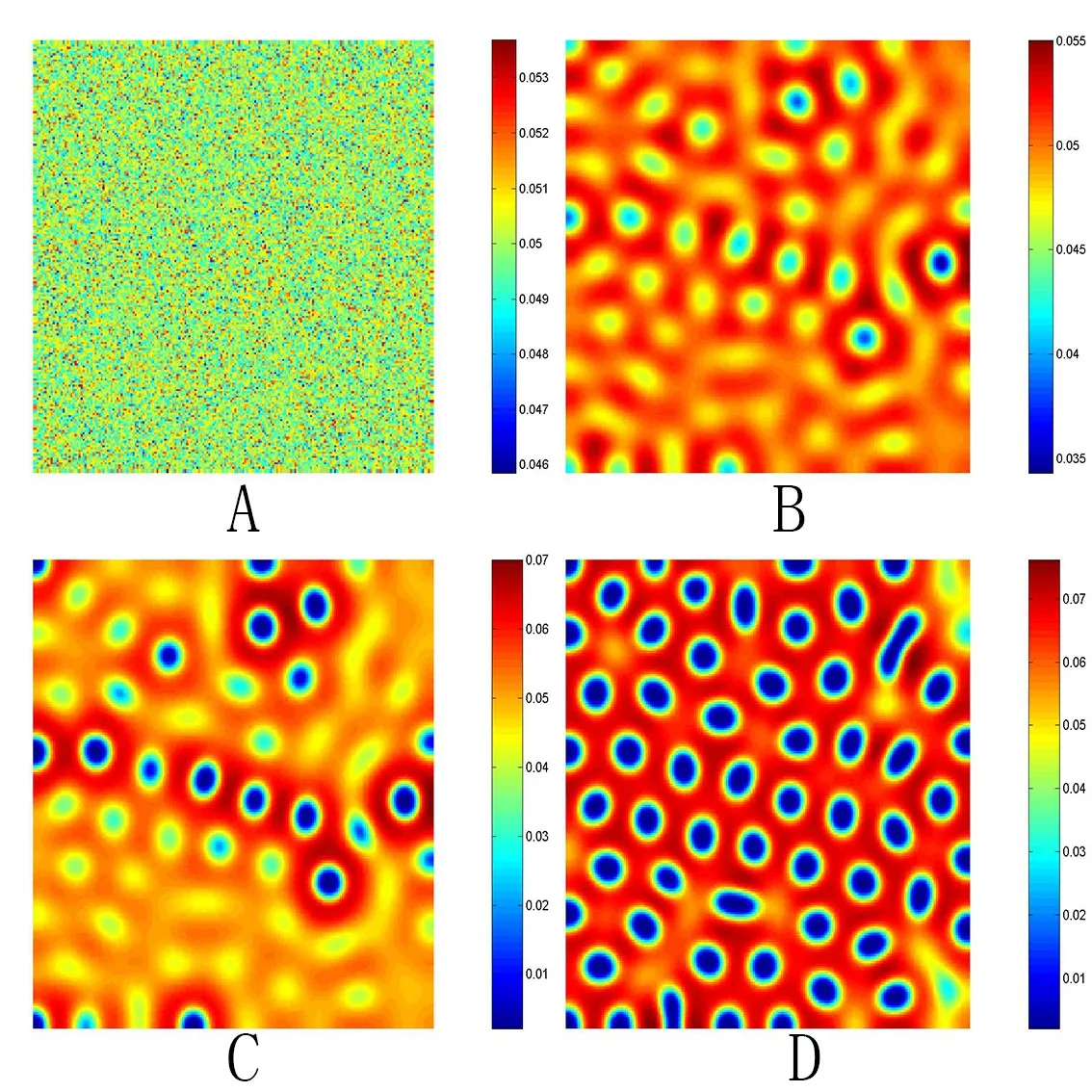
其中tr0=a11+a22,detJ=a11a22?a12a21.易知tr0<0和detJ>0當(dāng)且僅當(dāng)max{t1,t3}<β 通過Routh-Hurwitz,可知(S?,I?)是局部漸進(jìn)穩(wěn)定的. 現(xiàn)在考慮系統(tǒng)(1.3),并且對平衡點(diǎn)(S?,I?)進(jìn)行線性化分析.如下面所示,在平衡點(diǎn)(S?,I?) 處作微擾: 這里pλ是在時(shí)間t上的擾動增長率;kx和ky是相應(yīng)的振幅;i是虛數(shù)單位并且有i2=?1;k=是波數(shù);S0和I0是兩個(gè)正常數(shù).把(2.2)式帶入系統(tǒng)(1.3),并且省略所有的非線性項(xiàng),可以得到特征方程 特征方程(2.3)的解為如下形式 其中 選擇β作為分支參數(shù).當(dāng)Im(λk)6=0和Re(λk)=0在k=0時(shí)成立,系統(tǒng)出現(xiàn)Hopf分支,這樣能得到Hopf分支曲線 利用穩(wěn)定性定理[9?11],可知道當(dāng)Im(λk)=0和Re(λk)=0在k=kT6=0時(shí)成立,Turing分支出現(xiàn),且波數(shù)kT滿足因此分支參數(shù)βT滿足如下Turing分支曲線 根據(jù)Hopf和Turing分支曲線[12,13],能得到Hopf分支區(qū)域和Turing不穩(wěn)定區(qū)域. 圖1:模型(1.3)的分支圖,其中d11=0.02,d22=5,d12=0.1,d21=?0.1 在圖1中,可以看到系統(tǒng)(1.3)的分支圖包含了Turing分支線和Hopf分支線,并且它們把γ?β參數(shù)空間分成了四個(gè)區(qū)域,區(qū)域D11被稱為Turing空間,在這里發(fā)生Turing失穩(wěn),區(qū)域D12被稱為Hopf空間,在這里發(fā)生Hopf失穩(wěn). 為了更好地理解參數(shù)對系統(tǒng)穩(wěn)定性的影響作用,在圖2,給出了隨參數(shù)d21變化的色散關(guān)系圖.線(3)對應(yīng)著Turing臨界值d21=?1.13,當(dāng)d21=?0.9>?1.13時(shí),Turing失穩(wěn)發(fā)生;當(dāng)d21=?1.2 圖2:Re(λ)(特征值λ的實(shí)部)和k的關(guān)系,γ=0.2,K=1,μ=0.12,d=0.08,c=0.04,α1=0.4,α2=0.5,d11=0.02,d22=5,d12=0.1,β=0.1380和不同的d21:線(1):d21=?0.05;線(2):d21=?0.9;線(3):d21=?1.13;線(4):d21=?1.2 在這一部分,我們將通過Matlab對系統(tǒng)(1.3)進(jìn)行一系列的數(shù)值模擬.所有的數(shù)值模擬均運(yùn)用齊次Neumann邊界條件.將空間區(qū)域離散為200×200個(gè)格子.對空間的離散采用有限差分法,設(shè)定空間步長為?h=0.25,對時(shí)間的離散采用歐拉方法,取定時(shí)間步長為?t=0.01. 首先設(shè)d11=0.02,d22=5,d12=0.1,γ=0.2,μ=0.12,β=0.1380,d=0.08,c=0.04,α1=0.4,α2=0.5.現(xiàn)在研究參數(shù)d21的不同值所產(chǎn)生的斑圖. 圖3:時(shí)間:(A)t=0;(B)t=20000;(C)t=40000;(D)t=800000 圖4:時(shí)間:(A)t=0;(B)t=56000;(C)t=70000;(D)t=490000 在圖3中,d21=?0.05,這時(shí)可見:(A)中顏色條數(shù)值基本不變,初值選取為平衡解加上一個(gè)隨機(jī)擾動;(B)中出現(xiàn)類條狀斑圖;(C)中出現(xiàn)條狀斑圖;(D)條狀斑圖幾乎占據(jù)了整個(gè)區(qū)域,且系統(tǒng)的動力學(xué)行為不再發(fā)生變化. 圖4,圖5分別是d21=?0.7和d21=?0.9時(shí),染病者的時(shí)間演化圖.由圖4和圖5可見:隨著時(shí)間的演化,最終點(diǎn)狀斑圖和條狀斑圖共存.但圖4中條狀斑圖占優(yōu);而當(dāng)d21達(dá)到?0.9時(shí),點(diǎn)狀斑圖會占優(yōu)(圖5(D)).由圖6可見,當(dāng)d21增至?1.1時(shí),最終點(diǎn)狀斑圖幾乎占滿整個(gè)空間. 圖5:時(shí)間:(A)t=0;(B)t=90000;(C)t=120000;(D)t=800000 圖6:時(shí)間:(A)t=0;(B)t=520000;(C)t=600000;(D)t=800000 本文研究了在Neumann邊界條件下,負(fù)交叉擴(kuò)散對帶有非線性傳染率的傳染病模型的影響.具體表現(xiàn)為負(fù)交叉擴(kuò)散可引起系統(tǒng)(1.3)在平衡點(diǎn)E?處的Turing失穩(wěn),并由此得到了不同類型的斑圖,包括點(diǎn)狀斑圖、條形斑圖和點(diǎn)條混合斑圖.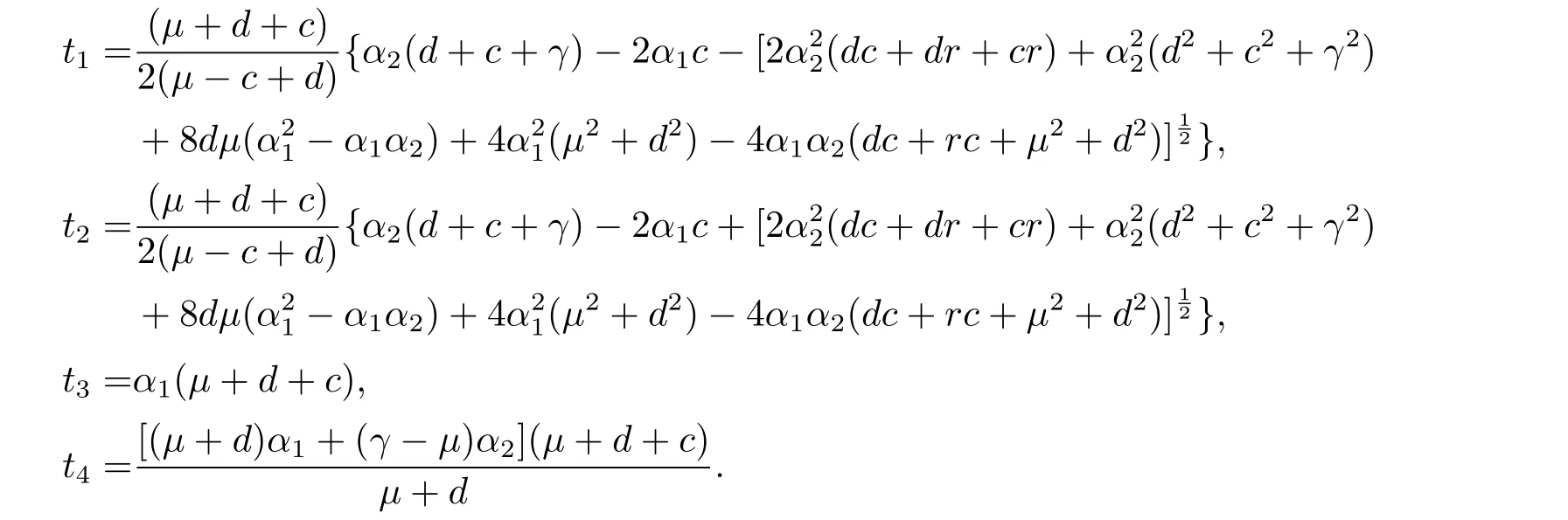
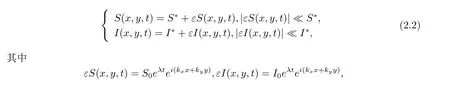
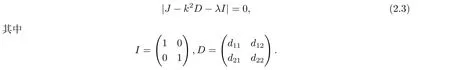

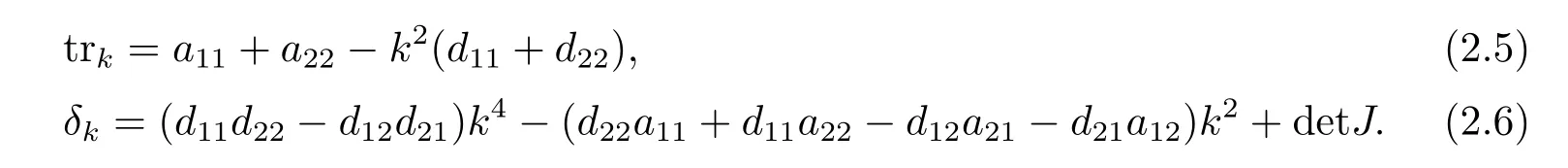


3 數(shù)值模擬
4 結(jié)論
- 數(shù)學(xué)雜志的其它文章
- WEIGHTED MIXED INEQUALITIES ON PRODUCT SPACES WITH MUCKENHOUPT BASES
- OPTIMAL TIME-CONSISTENT INVESTMENT AND REINSURANCE STRATEGIES FOR MEAN-VARIANCE INSURER UNDER THE DEPENDENT RISK MODEL
- CONSTACYCLIC CODES OF LENGTH 2sOVER F2+uF2+vF2+uvF2
- HIGH-DIMENSIONAL VARIABLE SELECTION WITH THE GENERALIZED SELO PENALTY
- OPTIMAL DIVIDENDS WITH EXPONENTIAL AND LINEAR PENALTY PAYMENTS IN A DUAL MODEL
- CHARACTERIZATIONS OF SOBOLEV CLASSES OF BANACH SPACE-VALUED FUNCTIONS ON METRIC MEASURE SPACE

