CHARACTERIZATIONS OF SOBOLEV CLASSES OF BANACH SPACE-VALUED FUNCTIONS ON METRIC MEASURE SPACE
LONG Pin-hong,HAN Hui-li,WANG Wen-shuai
(School of Mathematics and Statistics,Ningxia University,Yinchuan 750021,China)
Abstract:In the paper,we investigate the Sobolev function classes on Euclidean space when the index is infinity and the ones of Banach space-valued functions on metric measure space when the index is constant.By using the method of Banach space and potential theory,we give various characterizations of Sobolev classes of Banach space-valued functions on metric measure space when the index is infinity.Moreover,we compare the Sobolev classes with the corresponding Lipschitz and Hajlasz-Sobolev classes,which generalizes the related ones for Sobolev classes of Banach space-valued functions on metric measure space as well as Euclidean setting.
Keywords: Sobolev class;Banach space-valued function;Lipschitz function;Poincaré inequality;metric measure space
1 Introduction
The complete metric measure space X=(X,d,μ)is equipped with a metric d and a Borel regular outer measureμsuch that 0<μ(B(x,r))<∞for all balls B(x,r)={y∈X:d(x,y) Let(X,d)be a metric space and V an arbitrary Banach space of positive dimension.We call that a measurable map F:X → V belongs to the Sobolev class N1,∞(X:V)with the norm if F ∈ L∞(X:V)and if there exists a Borel function ρ :X → [0,∞]so that ρ ∈ L∞(X)and that for∞-a.e rectifiable curve γ :[a,b]→ X,where each function ρ is called an ∞-weak V-upper gradient of F and the norm k ·kN1,∞(X:V)satisfies the equivalence relation by F1=F2μ-a.e.if and only if k F1? F2kN1,∞(X:V)=0.If ρ satisfies(1.1)for all rectifiable curves γ,then ρ is called a V-upper gradient of F. The map F:X→V is C-Lipschitz if there exists a constant C>0 so that holds for x,y∈X,here k·k is the norm of element in V.Given a map F,the pointwise Lipschitz constant of F at non-isolated point x∈X is defined as follows If x is an isolated point,we define LipF(x)=0.LIP∞(X:V)is the space of bounded Lischitz maps F from X to V with the norm Let Λ = Λ(X)denote the family of all nonconstant rectifiable curves γ and ΓEthe family of all rectifiable curves γ such that γ ∩ E 6= φ.For Γ ? Λ,define the ∞-modulus of Γ by here F(Γ)is the family of all Borel measurable functions ρ :X → [0,∞]such that If some property holds for all γ ∈ ΛΓ with Mod∞(Γ)=0,then we call that the property holds for∞-a.e.curve. For each 1-Lipschitz function ? :V → R,the map ? ?F:X → R belongs to N1,∞(X),and there exists ρ ∈ L∞(X)that is an upper gradient of ??F for all such ?.The ∞-capacity of a set E ? X with respect to the space N1,∞(X:V)is defined by where the infimum is taken over all maps F in N1,∞(X:V)such that ? ? F|E≥ 1 for all 1-Lipschitz functions ?.We remark that if V=R and ? =1,the definition is the classical case for metric measure space(due to Cartagena[1]).Clearly,for E1?E2,it satisfies that Cap∞(E1:V)≤ Cap∞(E2:V). In the paper,the aim is to consider the properties related to Sobolev classes of Banach space-valued functions on metric measure space.In the classical Euclidean setting the generalizations of the theory of Sobolev spaces were based on the distributional the derivatives,we may refer to the books[2]and[3].The definitions of Sobolev classes of real-valued functions on metric measure spaces were given by Cheeger[4],Hajlasz[5,6],Koskela[7],Romanovskiˇi[8],Shanmugalingam[9],etc.There were many applications in areas of analysis,particularly the first order differential calculus,for example,nonlinear potential theory[10–12],quasiconformal and quasiregular theories[13,14],Carnot groups[15]and fractal analysis[16].To overcome the difficulties of derivatives and extra hypothesis on metric measure spaces,Shanmugalingam[9]applied a nonnegative Borel function to take the place of distributional derivatives and defined the Newtonian space N1,p(X)for 1≤p<∞.In addition,Hajlasz[5]ever considered a integrable function named by Hajlasz gradient to play a role as the same as upper gradient and introduced Hajlasz-Sobolev space M1,p(X)for 1≤p<∞.Under the suitable conditions,Cartagena[1]pointed out that the all approaches to Sobolev type spaces,even the spaces which support Poincaré inequality,turn to be equivalent.Thus Cartagena et al.[1,17]studied the Newtonian space N1,∞(X)and Hajlasz-Sobolev space M1,∞(X)as well as the cases that Poincaré inequality holds.The works of Ambrosio[18],Korevaar-Schoen[19]and Reshetnyak[20]etc.,were about the Sobolev mappings from the domains in Euclidean or Riemannian space into a complete metric space.Since every metric space may be isometrically embedded in the Banach space ‘∞(·)of bounded functions,many mathematicians focused on the case when the target is an arbitrary Banach space,refer to Cheeger and Kleiner[21],Heinonen et al.[22],Jarvenpaa et al.[23],Wildrick and Zurcher[24],and the references therein.Motivated by the studies of Cartagena and Heinonen et al.,we prove the characterizations of N1,∞(X:V)and its comparisons with LIP∞(X:V)and M1,∞(X:V)(refer to the definition in Section 2). The remainder of the paper is organized as follows:in Section 2 we will establish our main theorems;in Section 3,some preliminary lemmas will be given;in Section 4,we will prove the main results. Assume that Γ+Eis the family of all paths γ in Γ such that Lebeguse measure L1(γ?1(γ ∩ E))is positive.Denote by V?the dual space of V,which is endowed with the norm At first,we consider Newtion-Sobolev classes N1,∞(X:V)of Banach space-valued functions on metric measure space X. Theorem 2.1 Let X=(X,d,μ)be a metric measure space of finite total measure and V a Banach space.For each map F ∈L∞(X:V),there exists four equivalent results as follows: (I)F ∈ N1,∞(X:V); (II)for each 1-Lipschitz function ? :V → R,the map ? ?F:X → R belongs to N1,∞(X),and there exists ρ ∈ L∞(X)that is an ∞-weak upper gradient of ? ? F for all such ?; (III)for each v?∈ V?with k v?k≤ 1,the map hv?,Fi:X → R belongs to N1,∞(X:V),and there exists ρ ∈ L∞(X)that is an ∞-weak upper gradient of hv?,Fi for all such v?; (IV)for each z∈F(X),the map dzF:X→R defined by dzF(x)=k F(x)?z k belongs to N1,∞(X:V),and there exists ρ ∈ L∞(X)that is an ∞-weak upper gradient of dzF for all such z. It is well known that the space with the doubling measure can be isometrically embedded into a separable Banach space.If X is equipped with the doubling measure,then we may obtain three results being equivalent to the four ones above. (V)for each 1-Lipschitz function ? :V → R,the map ? ?F:X → R belongs to N1,∞(X),and there exists∈L∞(X)such that ρ??F≤for all such ?; (VI)for each v?∈ V?with k v?k≤ 1,the map hv?,Fi:X → R belongs to N1,∞(X:V),and there exists ρ ∈L∞(X)such that ρ??F≤for all such v?; (VII)for each z∈F(X),the map dzF:X→R defined by dzF(x)=k F(x)?z k belongs to N1,∞(X:V),and there exists ρ ∈L∞(X)such that ρ??F≤for all such z. Following the ways of Cartagena(see[1])and Shanmugalingam(see[9]),by some extra techniques we may establish the next theorems on F ∈ N1,∞(X:V). Theorem 2.2 Let Fi∈ N1,∞(X:V)and ρi∈ L∞(X)be an ∞-weak V-upper gradient of Fifor i∈ N.Suppose that there exist F ∈ L∞(X:V)and ρ ∈ L∞(X)so that the sequences{Fi}and{ρi}converge to F in L∞(X:V)and ρ in L∞(X),respectively.Then there exists a mapeF=F μ-a.e.such that ρ is an ∞-weak V-upper gradient ofeF.Moreover,eF ∈ N1,∞(X:V). Theorem 2.3 N1,∞(X:V)is a Banach space.Moreover,every map F ∈ N1,∞(X:V)has a minimal∞-weak V-upper gradient ρFin L∞(X). For 1≤p≤∞,the Hajlasz-Sobolev space M1,p(X:V))is the set of all maps F∈Lp(X:V)with the norm for which there exists a nonnegative function g∈Lp(X)such that here k·kM1,p(X:V)also satisfies the equivalence relation by F1=F2μ-a.e.if and only if k F1?F2kM1,p(X:V)=0. For F∈L1(X:V)and E?X withμ(E)>0,define the mean value of F over the set E by the vector For λ ≥ 1 and an open ball B(x,r)in X,let F ∈ L1(λB(x,r):V)and ρ :λB(x,r) →[0,∞]be a Borel measurable function.If there exists a constant Cpfor 1≤p<∞so that holds,then we call that the function pair(F,ρ)satisfies the weak p-Poincaré inequality in λB(x,r).Next it shows the relations among LIP∞(X:V),N1,∞(X:V)and M1,∞(X:V)in the sense of equivalent norm. Theorem 2.4 Suppose that X supports a weak p-Poincaré inequality for 1 ≤ p< ∞and the doubling Borel measure μ.Then LIP∞(X:V)=N1,∞(X:V)=M1,∞(X:V)with equivalent norms. Before we continue to deal with our arguments,we will recall and prove the following lemmas. Lemma 3.1(see[1],Lemma III.2.9 for p= ∞ and Fuglede[25]for 1≤ p< ∞)Let ρk:X → [?∞,+∞]be a sequence of Borel functions which converge to a Borel representative ρ in Lp(X).Then there exists a subsequence{ρkn}of Borel functions such that for p-a.e.curve γ∈Λ,where 1≤p≤∞. Lemma 3.2(see[1],Lemma III.2.6)Ifμ(E)=0 for E ? X,then Mod∞(Γ+E)=0. Lemma 3.3 If{Ek}is a sequence in X,then Proof Obviously,we only need to consider the case for?>0 and positive integer k,we may choose a sequence of maps Uk∈ N1,∞(X:V)with ??Uk|Ek≥ 1 for all 1-Lipschitz functions ? and ∞-weak V-upper gradient%kof ??Uksuch that where ρnis an ∞-weak V-upper gradient of ? ? Fn.Then%kkL∞(X)are finite.It implies that Therefore,{Fn}is a Cauchy sequence which converges toV).Similarly,{ρn}converges toAccording to Theorem 2.2 there exists a map=F μ-a.e.such that ρ is an ∞-weak V-upper gradient ofMoreover,∈ N1,∞(X:V).Since ? ?F ≥ 1 inwe obtain that which is the desired result and so Lemma 3.3 holds. Lemma 3.4 If Cap∞(E:V)=0 for E ? X,then Mod∞(ΓE)=0. Proof For?>0 and positive integer k,we may choose a sequence of maps Uk∈N1,∞(X:V)with ??Uk|E≥ 1 for all 1-Lipschitz functions ? and ∞-weak V-upper gradient%kof ??Uksuch that where ρnis an ∞-weak V-upper gradient of ? ? Fn.Following the procedure of proof in Lemma 3.3 there exists a map=F μ-a.e.such that ρ is an ∞-weak V-upper gradient of eF.Moreover,eF ∈ N1,∞(X:V).By Theorem 2.2,we infer that outside a set G satisfying Mod∞(ΓG)=0.Since E ? G,that is to say ΓE? ΓG,we have Mod∞(ΓE)≤ Mod∞(ΓG)and it follows Mod∞(ΓE)=0. Lemma 3.5(see Cartagena[1],Lemma III.2.5)For Γ ∈ Λ,the following results are equivalent: (I)Mod∞(ΓE)=0; (II)there exists a nonnegative Borel function ρ ∈ L∞(X)such thateach γ ∈ Γ; (III)there exists a nonnegative Borel function ρ ∈ L∞(X)such thateach γ ∈ Γ and k ρ kL∞(X)=0. Lemma 3.6(see Cartagena[1],Theorem III.3.3)Suppose that X supports a weak p-Poincaré inequality for 1 ≤ p< ∞ and the doubling Borel measure μ which is nontrivial and finite on balls.For nonnegative ρ ∈ L∞(X),there exists a set E ? X of measure zero and positive constant K depending only on X such that for all x,y∈XE there exists a rectifiable curve γ connecting x and y so that Proof of Theorem 2.1 Assume that result(I)is true.Let ρ ∈ L∞(X)be an ∞-weak V-upper gradient of F and ? :V → R be 1-Lipschitz function.If γ is a rectifiable curve in X with the ends x and y,then Since X has finite mass,we obtain that Therefore, ? ? F is in N1,∞(X:V)and ρ is an ∞-weak upper gradient of ? ? F which is independent of ?.Hence,it follows result(II). Since both the mappings hv?,·i:V → R with k v?k≤ 1 for v?∈ V?and the mappings dz:V→R with dz(v)=k v?z k for z∈V are 1-Lipschitz,by(II),results(III)and(IV)clearly hold. Suppose that the map F ∈ L∞(X:V)and ρ ∈ L∞(X)satisfy result(III).Let γ be a rectifiable curve in X with the ends x and y.If F(x)=F(y),then the result is trivial.Otherwise,we choose v?∈V?satisfying with k v?k≤ 1.Since ρ is an ∞-weak upper gradient of hv?,Fi for all such v?,we know that Hence,ρ is an ∞-weak V-upper gradient of F and so F ∈ N1,∞(X:V).Similarly,from result(IV)it infers(I).When X is equipped with the doubling measure,we may assume that F(X)is separable.For the equalities of(I),(V),(VI)and(VII),we only need repeat the procedures of Heinonen et al.[22]. Proof of Theorem 2.2Set Since Fi→ F in L∞(X:V),clearly it convergesμ-a.e.Hence=F μ-a.e.andeF ∈L∞(X:V).Therefore,the mapis well defined outside the zero-measurable set where ? :V → R is 1-Lipschtiz function.Let Γ be the collection of paths γ ∈ Λ such that either From Lemma 3.1,it easily infers that Mod∞(Γ)=0.Since μ(E)=0,by Lemma 3.2 we know that Mod∞()=0.For any nonconstant path γ ∈ Λ (Γ ∪),we may fix a point y ∈|γ |E,here|γ |is the image of γ.Since ρkis an ∞-weak V-upper gradient of Fk,we know that for all points x∈|γ|, and so x ∈ XE.That is to say,γ ∈ ΓEfails and so ΓE? Γ∪Further Mod∞(ΓE)=0. For γ ∈ Λ Γ,let x and y be the end of points of its images.Clearly,x,y don’t belong to E,and so we know that Proof of Theorem 2.3 For a Cauchy sequence{Fk}in N1,∞(X:V),it can be assumed that and k ρk+1,kkL∞(X:V)<2?k,where ρk,‘is an ∞-weak V-upper gradient of Fk? F‘. Let If x∈G fails,then exists‘satisfying and thus the Cauchy sequence{Fk(x)}converges in X.Here we putNow we claim that the set G is of∞-capacity zero.Since 2kk Fk+1(x)?Fk(x)k≥ 1 holds on Ek,we know that From the countably subadditivity of Cap∞(·:V)in Lemma 3.3,we obtain that Hence Cap∞(G:V)=0. When x∈XG,the sequence{Fk(x)}is convergent.Therefore,we know that By Lemma 3.4,we get that Mod∞(ΓG)=0.For γ ∈ Λ ΓGbeing connected x and y,we have that Hence,{Fk}converges into F in N1,∞(X:V).That is to say,N1,∞(X:V)is a Banach space. On the other hand,from Theorem 2.2,we may choose a sequence{ρk}satisfying ρk→ρ=inf{%k}as k→ ∞ in L∞(X)so that there exists a map eF=F μ-a.e.such that ρ is an∞-weak V-upper gradient of eF,that is to say,ρ is an∞-weak V-upper gradient of F.Thus Theorem 2.3 follows. Proof of Theorem 2.4 According to the definitions of LIP∞(X:V)and M1,∞(X:V),we easily see thatM1,∞(X:V).Assume that F ∈ N1,∞(X:V).Then there exists an ∞-weak V-upper gradient ρ ∈ L∞(X)of F.Now we denote by ΓNthe family of curves for which ρ is not a V-upper gradient of F,and so Mod∞(ΓN)=0.From Lemma 3.5,we know that there exists a nonnegative Borel function∈L∞(X)such thatwhich is a V-upper gradient of F and satisfiesBy Lemma 3.5 we remark that∞-modulus zero.Therefore,if From Lemma 3.6,there exists a set E?X of measure zero and positive constant K depending only on X such that for all x,y ∈ XE there exists a rectifiable curve γ connecting x and y so that Then F is K k ρ kL∞(X)-Lischitz μ-a.e.That is to say,there exits aeF ∈ LIP∞(X:V)so that F=eF holds μ-a.e.Therefore,LIP∞(X:V)=N1,∞(X:V).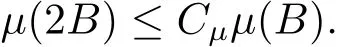
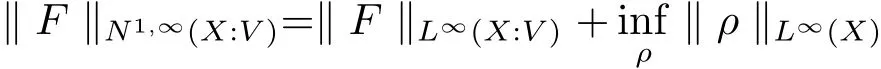
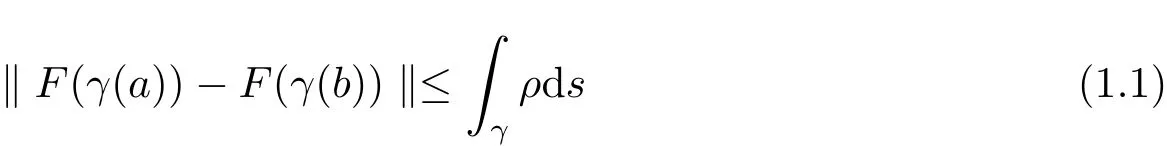

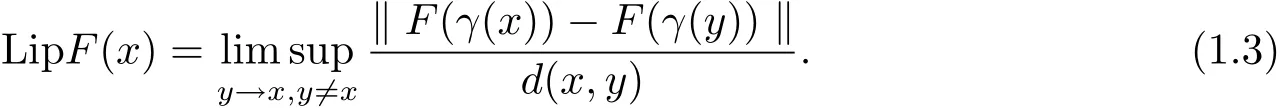
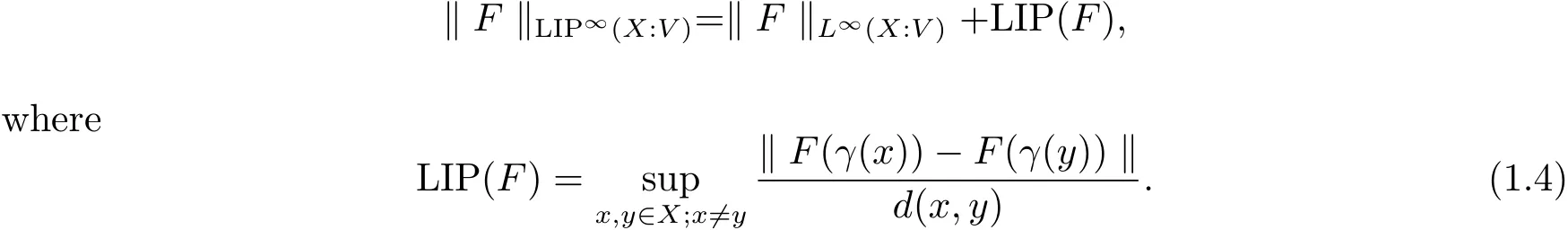
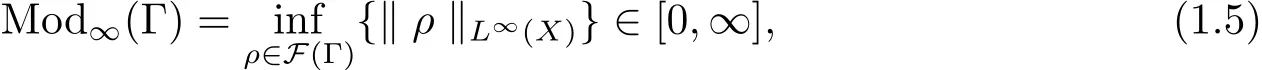
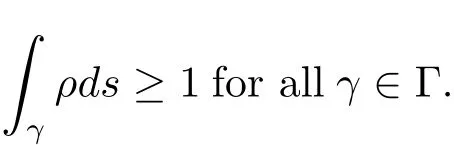
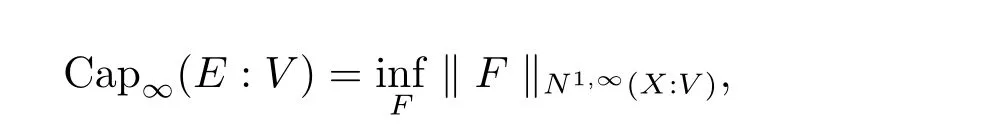
2 Statements of Main Results

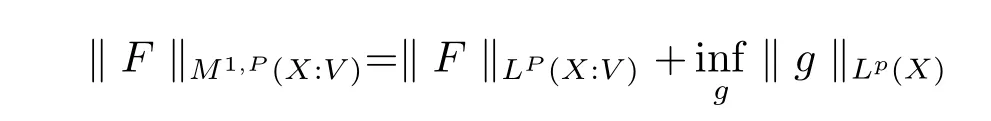
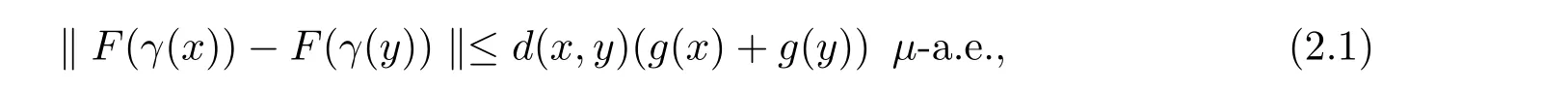
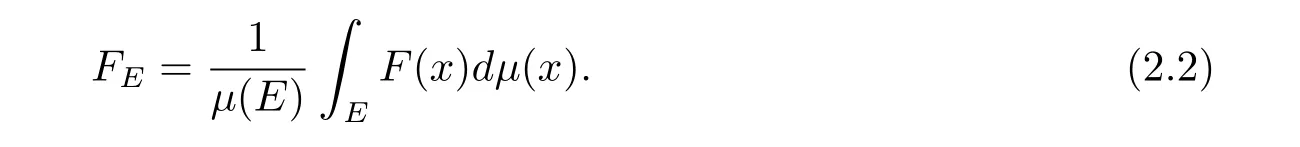
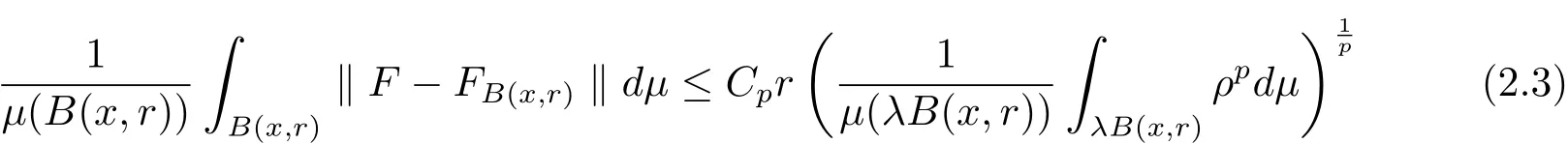
3 Some Preliminary Lemmas
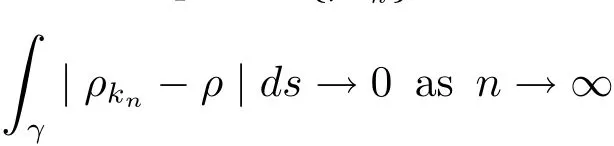
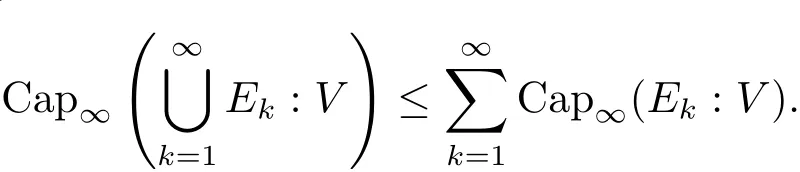
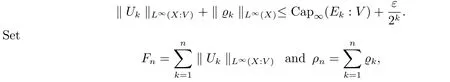
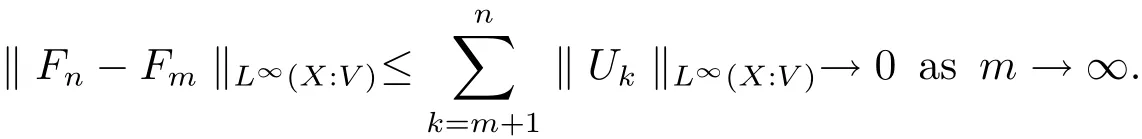
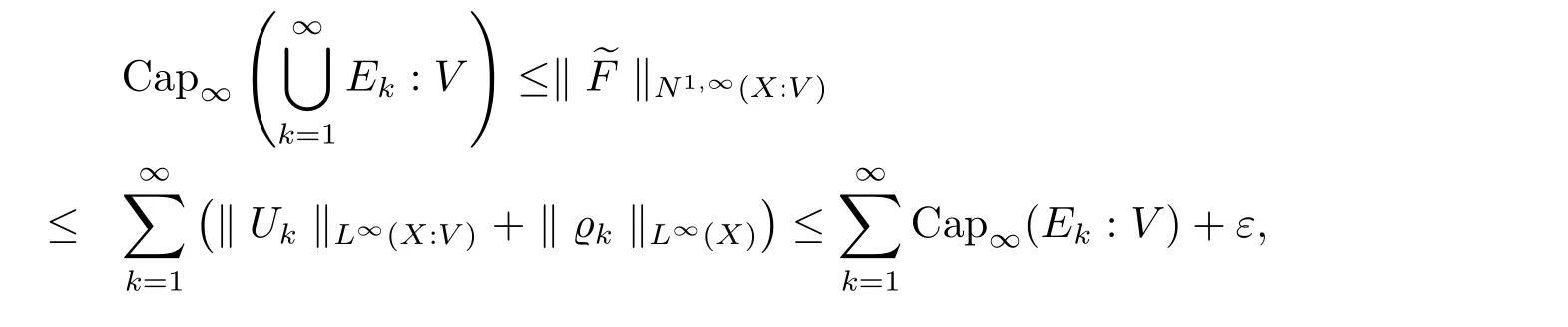

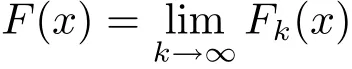
4 Proofs of Main Theorems
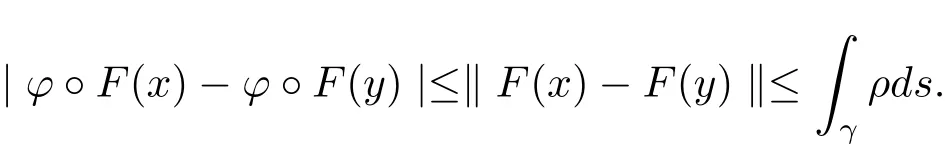
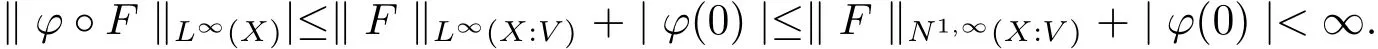
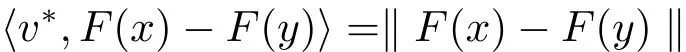
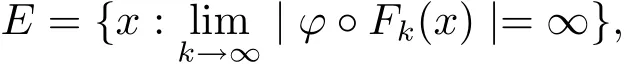
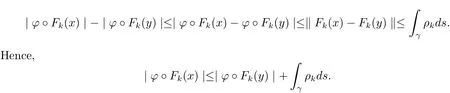
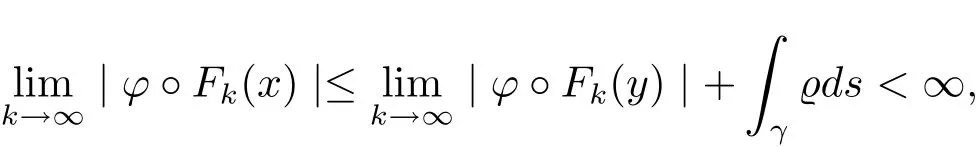
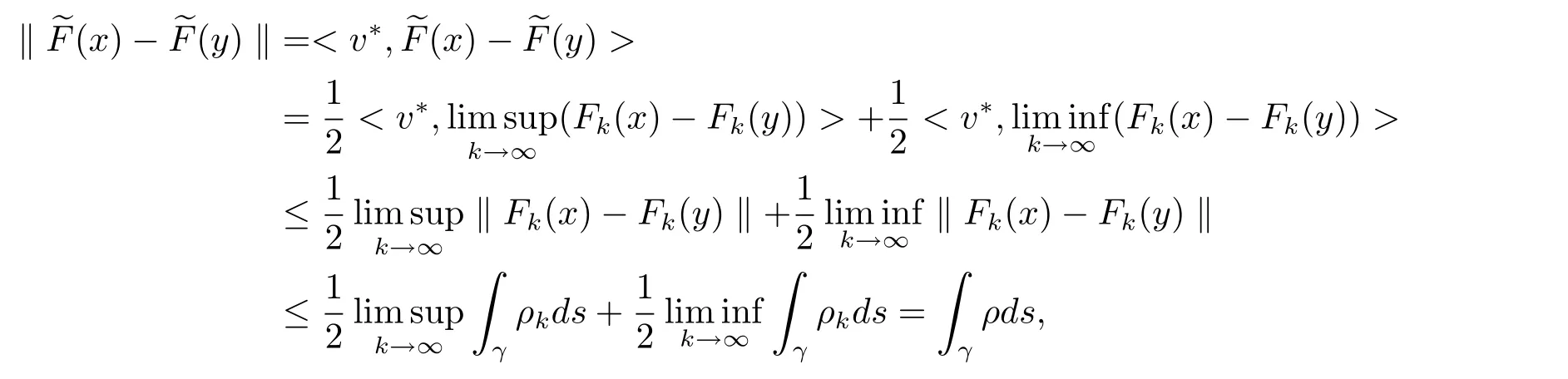
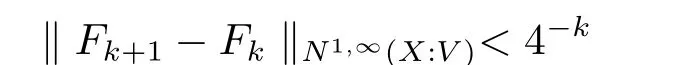
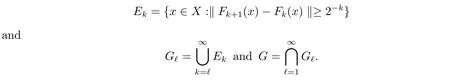
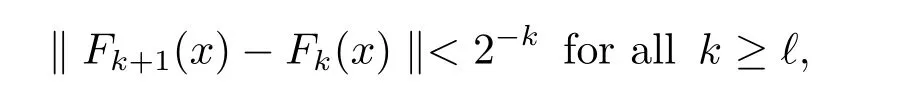
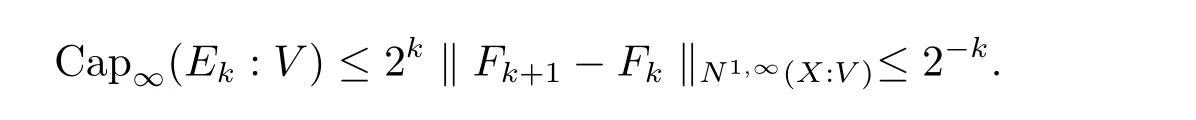
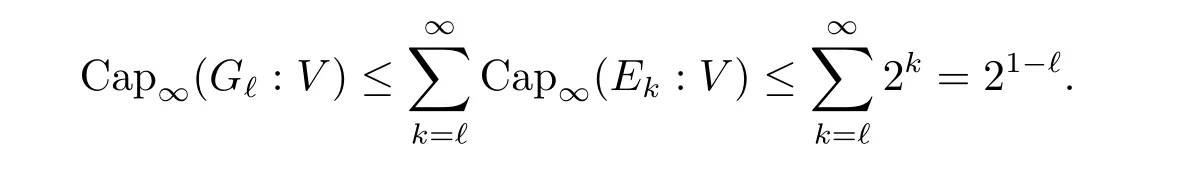

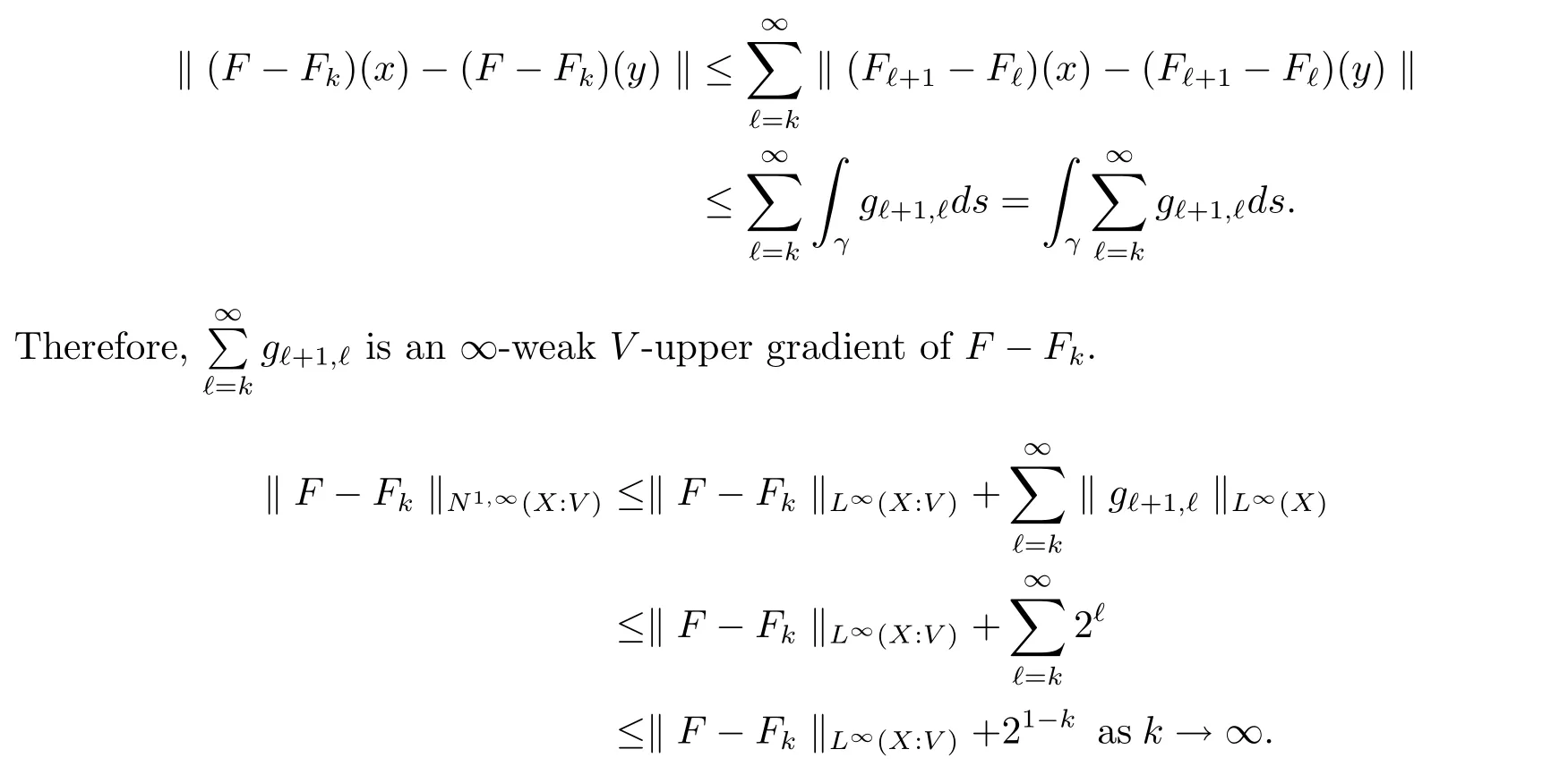
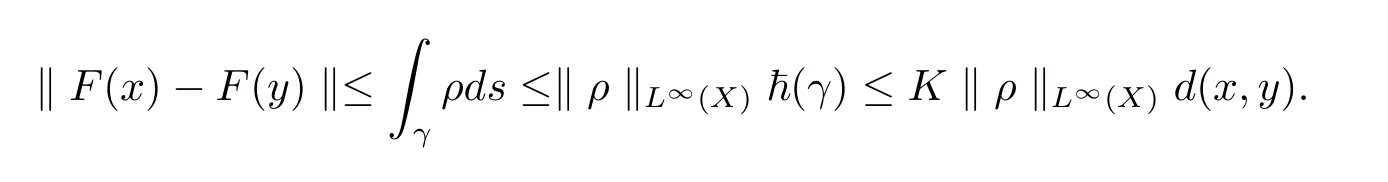
- 數(shù)學(xué)雜志的其它文章
- WEIGHTED MIXED INEQUALITIES ON PRODUCT SPACES WITH MUCKENHOUPT BASES
- OPTIMAL TIME-CONSISTENT INVESTMENT AND REINSURANCE STRATEGIES FOR MEAN-VARIANCE INSURER UNDER THE DEPENDENT RISK MODEL
- CONSTACYCLIC CODES OF LENGTH 2sOVER F2+uF2+vF2+uvF2
- HIGH-DIMENSIONAL VARIABLE SELECTION WITH THE GENERALIZED SELO PENALTY
- OPTIMAL DIVIDENDS WITH EXPONENTIAL AND LINEAR PENALTY PAYMENTS IN A DUAL MODEL
- A MODIFIED STRATEGY IN ALTERNATING NON-NEGATIVE LEAST SQUARES FOR NON-NEGATIVE MATRIX FACTORIZATION

