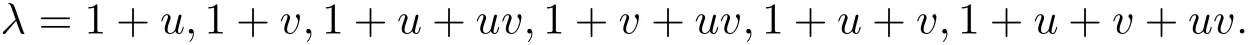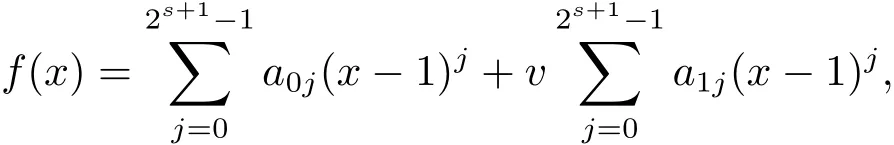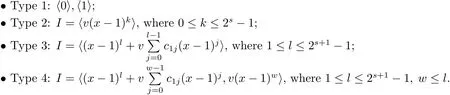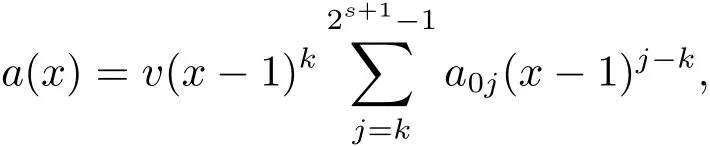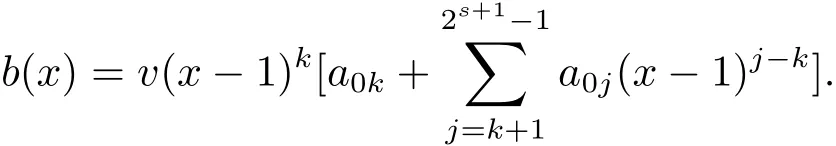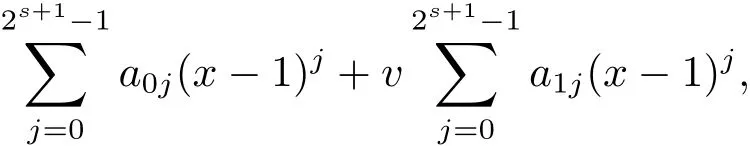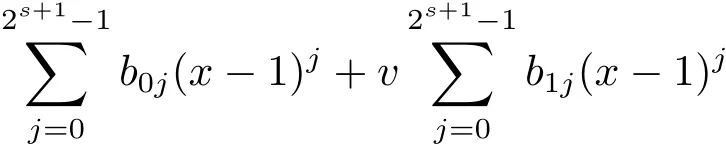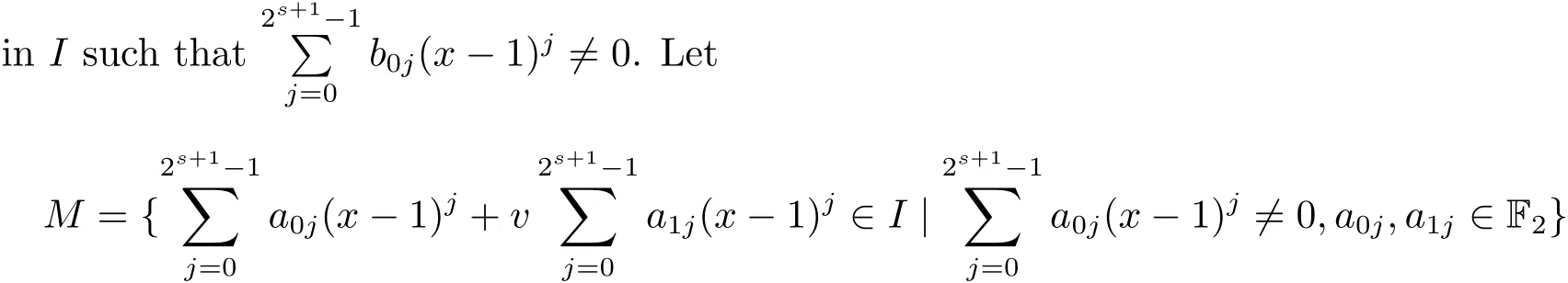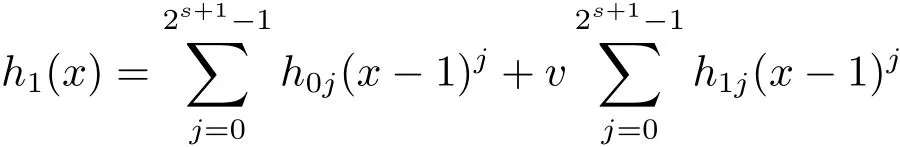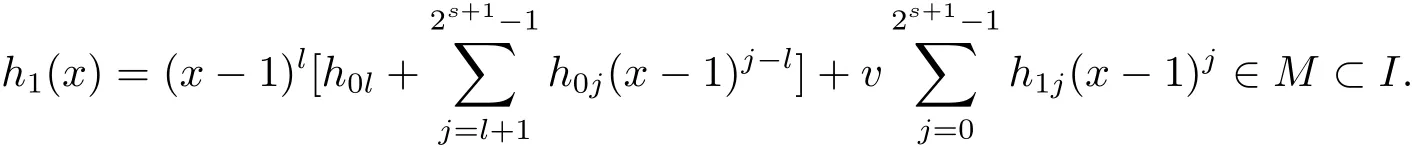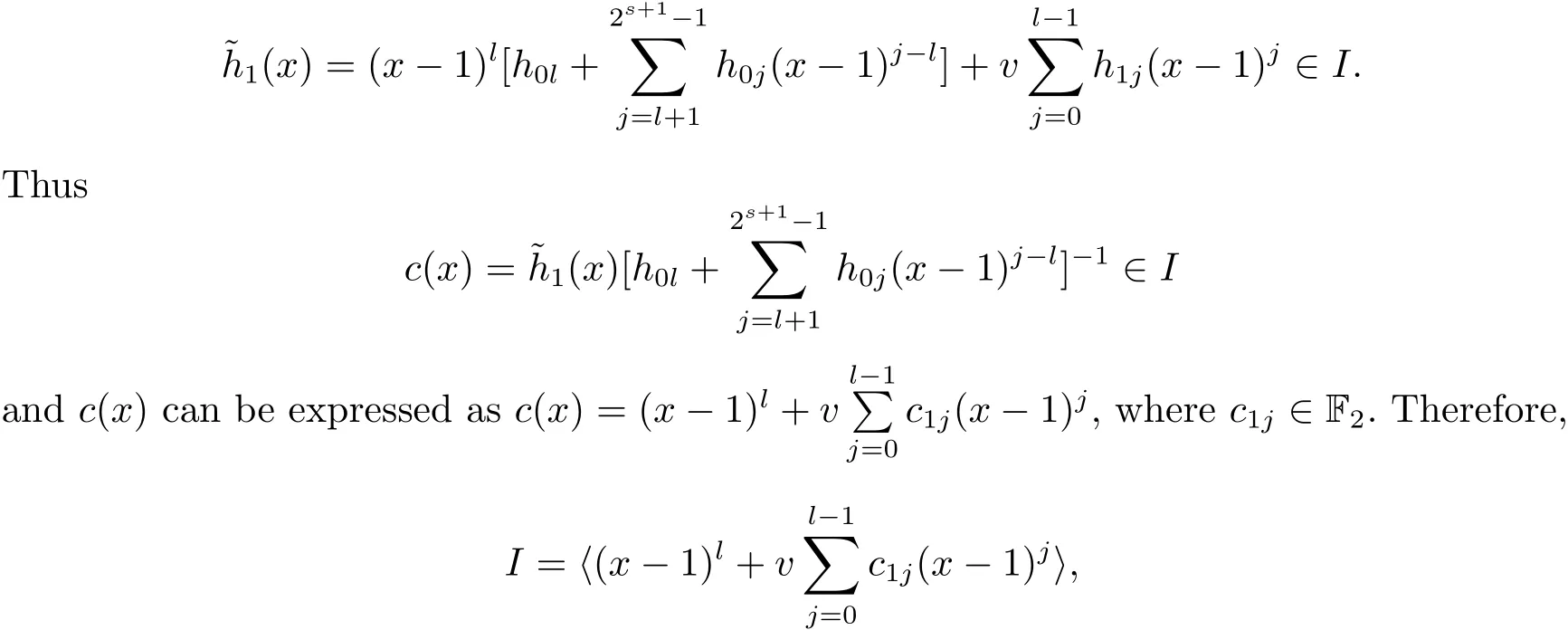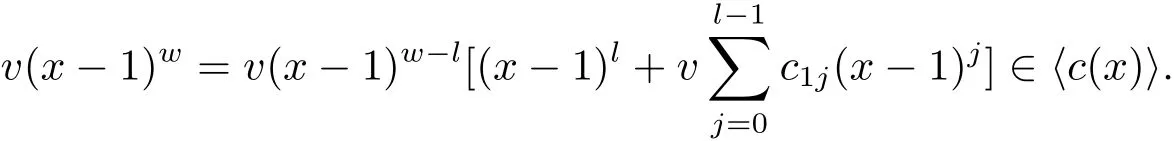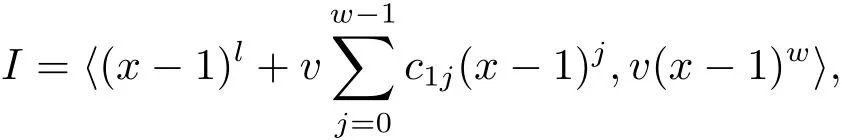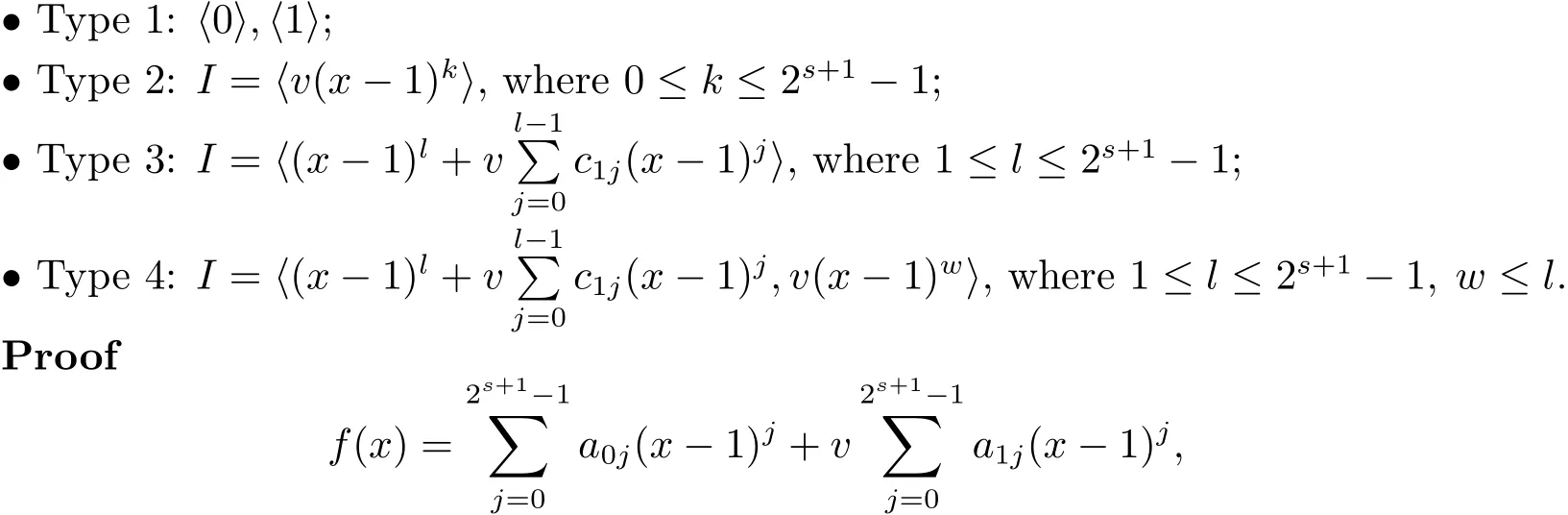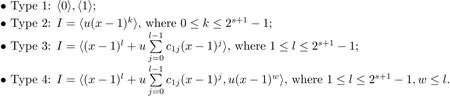CONSTACYCLIC CODES OF LENGTH 2sOVER F2+uF2+vF2+uvF2
LIU Xiu-sheng,XU Xiao-fang,HU Peng
(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China)
Abstract:In this paper,we investigate all constacyclic codes of length 2sover R=F2+uF2+vF2+uvF2,where R is a local ring,but it is not a chain ring.First,by means of the Euclidean algorithm for polynomials over finite commutative local rings,we classify all cyclic and(1+uv)-constacyclic codes of length 2sover R,and obtain their structure in each of those cyclic and(1+uv)-constacyclic codes.Second,by using(x?1)2s=u,we address the(1+u)-constacyclic codes of length 2sover R,and get their classification and structure.Finally,by using similar discussion of(1+u)-constacyclic codes,we obtain the classification and the structure of(1+v),(1+u+uv),(1+v+uv),(1+u+v),(1+u+v+uv)-constacyclic codes of length 2sover R.
Keywords: constacyclic codes;cyclic codes;local ring;repeated-root constacyclic codes
1 Introduction
Codes over the ring R=F2+uF2+vF2+uvF2were introduced in[1].The ring R is a characteristic 2 ring of size 16.It turns out to be a commutative,non-chain,and a local Frobenius ring constructed subject to u2=v2=0,uv=vu.It can be viewed as a natural extension of the ring F2+uF2,which was studied quite extensively in[2]and[3].In particalar,the ring F2+uF2is interesting because it shares some good properties of both Z4and Galois field F4.(1+u)-constacyclic codes over F2+uF2of odd length were first introduced by Qian et al.in[4],where it proved that the Gray image of a linear(1+u)-constacyclic code over F2+uF2of odd length is a binary distance invariant linear cyclic code.Recently,Yildiz and Karadeniz in[5,6]studied constacyclic codes of odd length over R.They found some good binary codes as the Gray images of these cyclic codes.The authors in[7]considered the more general ring,and studied the general properties of cyclic codes over these rings and characterized the nontrivial one-generator cyclic codes.Kemat et al.in[8]extended these studies to cyclic codes over the ringwhere u2=0,v2=0,uv=vu and p is a prime number.
In this paper,we study repeated-root λ-constacyclic codes of length 2sover R,where λ is unit of R.Although repeated-root λ-constacyclic codes over finite ring?R are known to be asymptotically bad,they are optimal in a few cases.They motivated the researchers to further study(see[9–15]).
The paper is organized as follows.In Section 2,we recall some notations and properties about constacyclic codes over finite local rings.In Section 3,we address the cyclic and(1+uv)-constacyclic codes of length 2sover R.We classify all such cyclic and(1+uv)-constacyclic codes by categorizing the ideals of the local ring R1=into 13 types.In the last section,we study the(1+u)-constacyclic codes of length 2sover R.These(1+u)-constacyclic codes are the ideals of the ring with the maximal ideal.We classify all(1+u)-constacyclic codes by categorizing the ideals of the local ring R3into 4 type,and provide a detailed structure of ideal in each type.By using similar discussion of(1+u)-constacyclic codes,we obtain the classification and the structure of(1+v),(1+u+uv),(1+v+uv),(1+u+v),(1+u+v+uv)-constacyclic codes of length 2sover R.which is a local ring
2 Basics
A code of length n over R is a nonempty subset of Rn,and a linear code C of length n over R is an R-submodule of Rn.If λ is a unit in R,a linear code C is called as λconstacyclic if(λan?1,a0,···,an?2) ∈ C for every(a0,a1,···,an?1) ∈ C.It is well known that a λ-constacyclic code of length n over R can be identified as an ideal in the residue ringvia the R-module isomorphism ? :given by
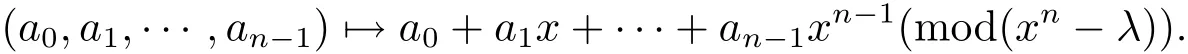
If λ =1, λ-constacyclic codes are just cyclic codes and if λ = ?1, λ-constacyclic codes are known as negacyclic codes.A polynomial is said to be regular if it is not a zero divisor.The following version of the Euclidean algorithm holds true for polynomials over finite commutative local rings.
Proposition 2.1(see[16,Example,III.6])Letbe a finite commutative local ring,and f,g be nonzero polynomials inR?[x].If g is regular,then there exist polynomials q(x),r(x)∈R?[x]such that f(x)=q(x)g(x)+r(x)and r(x)=0 or deg(r(x)) Cyclic codes of length 2sover R are ideals of the residue ring,and the(1+uv)-constacyclic codes of length 2sover R are ideals of the residue ring It is easy to prove the following three lemmas. Lemma 3.1 The following hold true in R1: (i)For any nonegative integer t,(x?1)2t=x2t?1. (ii)x?1 is nilpotent with the nilpotency index 2s. Lemma 3.2 The following hold true in R2. (i)For any nonnegative integer t,(x?1)2t=x2t?1.In particular,(x?1)2s=uv. (ii)x?1 is nilpotent with the nilpotency index 2s+1. Lemma 3.3 Let f(x)∈R1or R2.Then f(x)can be uniquely expressed as where a0j,a1j,a2j,a3j∈F2.Furthermore,f(x)is invertible if and only if a006=0. Proposition 3.4 The ring R1or R2is a local ring with the maximal idealbut it is not a chain ring. Proof By Lemma 3.3,the ideal hu,v,x?1i is the set of all non-invertible elements of R1or R2.Hence R1or R2is a local ring with maximal ideal hu,v,x?1i.Suppose u∈Then there must exist f1(x)and f2(x)∈R[x]such that u=(x?1)f1(x)+(x2s?1)f2(x)or u=(x?1)f1(x)+[x2s?(1+uv)]f2(x).However,this is impossible because plugging in x=1 yields u=0 or u=uv.Hence,u/∈hx?1i.Similarly,v/∈.Next we suppose x?1∈hui or hvi.Then(x?1)2=0,which is a contradiction with s>1.Therefore,the maximal ideal hu,v,x?1i of R1or R2is not principal.It means R1or R2is not a chain ring. Theorem 3.5 All of cyclic codes of length 2sover R,i.e.,ideals of the ring R1are the following: Proof Ideals of Type 1 are the trivial ideals.Consider an arbitrary nontrivial ideals of R1. Case 1 I?hvi.Any element of I must have the form v1)j,where a0j,a1j∈F2. Let Suppose M 6= Φ.Setting α =min{deg(m(x))|m(x) ∈ M}.Then there is an element m1(x)=vPm0j(x?1)j+uvPm1j(x?1)j∈M with deg(m1(x))=α.It has the smallest t such that m0t6=0.Hence we have Then m1(t)=vm2(t). Now we have two subcases. Case 1.1 N?hm1(x)i.For any f(x)∈M,obviously,f(x)can be written as f(x)=vf1(x),where f1(x)=By Proposition 2.1,f1(x)can be written as f1(x)=q(x)m2(x)+r(x),where q(x),r(x)∈R1and r(x)=0 or deg(r(x)) Case 1.2 N*hm1(x)i.Then there exists the smallest integer z such that n(x)=uv(x?1)zn1(x)for every n(x)∈ N,where n1(x)∈ R1.It is easy to verify that uv(x?1)z∈ N,but uv(x?1)z/∈hm1(x)i,and z Therefore,I is in Type 4. Case 2 hvi I?hu,vi.Any element of I must have the form Again we have two subcases. Case 2.2.1 N1=Φ.Then N26={0}.Therefore,there exists the smallest integer t such that n2(x)=uv(x?1)tq(x)for every n2(x)∈N2=N,where q(x)∈R1.It is easy to verify that uv(x?1)t∈N2=N.Hence, Suppose that t≥l.Then where 1≤l≤2s?1.Therefore,I is in Type 6. Case 2.2.2 N16=Φ.Then there is an element in N1that has smallest z such that?a2z6=0.Hence we have For any n1(x)∈N1,obviously,n1(x)can be written as where a2j,a3j∈F2.Thus,we can assume that If N2={0},then where 0≤l≤2s?1,0≤z≤2s?1.Thus,I is in Type 7. If N26={0}.Then there exists the smallest integer w such that n2(x)=uv(x?1)wq(x)for every n2(x)∈N2,where q(x)∈R1.It is easy to verify that uv(x?1)w∈I.Hence, where 1≤l≤2s?1,1≤z≤2s?1,and w Case 3 I*hu,vi.Let Iu,v=there are g(x),h(x),m(x)∈1i such that f(x)+ug(x)+vh(x)+uvm(x)∈R1}.Then Iu,vis a nonzero ideal of the ringIt is a chain ring with ideals h(x?1)ji,where 0≤ j≤ 2s.Hence there is an integer i∈ {0,1,···,2s?1}such thatTherefore,there are three elements for i=1,2,3 such that(x?1)i+uc1(x)+vc2(x)+uvc3(x)∈I,whereBecause Hence it can be assumed without loss of generality that Now we have two subcases. and bf(x)can be expressed as where b0j,b1j,b2j,b3j∈F2.Now,by the definition of Iu,v,we have where 0≤i≤2s?1,0≤l≤2s?1 and t≤min{i,l}.Thus,I is in Type 11. where 0≤i≤2s?1,0≤l≤2s?1,0≤z≤2s?1 and w≤min{i,l,z}.Thus,I is in Type 13. Similar to discussion in Theorem 3.5,and note that(x?1)2s=uv,we have following theorem. Theorem 3.6(1+uv)-constacyclic codes of length 2sover R,i.e.,ideals of the ring R2are In this section,we discuss the λ-constacyclic codes,where First,we study the structure of the(1+u)-constacyclic codes of length 2sover R.Obviously,(1+u)-constacyclic codes of length 2sover R are ideals of the residue ringIt is easy to verify the following lemmas. Lemma 4.1 The following hold true in R3. (i)For any nonnegative integer t,(x?1)2t=x2t?1.In particular,(x?1)2s=u.(ii)x?1 is nilpotent with the nilpotency index 2s+1. Lemma 4.2 Let f(x)∈R3.Then f(x)can be uniquely expressed as where a0j,a1j∈F2.Furthermore,f(x)is invertible if and only if a006=0 Proof Since each element r∈R has a unique presentation r=r1+ur2+vr3+uvr4,where r1,r2,r3,r4∈F2,each element f(x)over R3can be uniquely represented as Because(x?1)2s=u in R3,it can be uniquely represented without loss of generalitywhere a0j,a1j∈F2.The last assertion follows from the fact that v and x?1 are both nilpotent in R3. Similar to the discussions in Proposition 3.3,we have the following proposition. Proposition 4.3 The ring R3is a local ring with the maximal ideals hv,x?1i,but it is not a chain ring. Following the proposition and lemmas above,we can list all(1+u)-constacyclic codes of length 2sover R3as follows. Theorem 4.4(1+u)-constacyclic codes of length 2sover R,i.e.,ideals of the ring R3are Proof Ideals of Type 1 are the trivial ideals.Consider an arbitrary nontrivial ideal of R3. Case 1 I?hvi.Any element of I must have the forma0j∈F2.Let b(x)∈I be an element that has the smallest k such that a0k6=0.Hence all element a(x)∈I have the form which implies I?hu(x?1)ki. On the other hand,we have b(x)∈I with As a0k6=0,a0k+is invertible,and v(x?1)k∈I.That is to say,the ideal of R3contained in hvi are hv(x?1)ki,0≤k≤2s+1?1.It means that I is in Type 2. Case 2 I*hvi.Any element of I must have the form and there exists a polynomial in H that has the smallest l such that h0l6=0.Hence we have Now,we have two subcases. Case 2.1 N?hh1(x)i.For any f(x)∈M,by Proposition 2.1,f(x)can be written as f(x)=q(x)h1(x)+r(x),where q(x),r(x)∈R3,and r(x)=0 or deg(r(x)) where 1≤l≤2s+1?1.Hence I is in Type 3. Case 2.2 N*hh1(x)i=hc(x)i.Then there exists the smallest integer w such that n(x)=v(x?1)wn1(x)for every n(x)∈N,where n1(x)∈R3.Obviously,v(x?1)w∈N,but v(x?1)w/∈hh1(x)i=hc(x)i.Hence I= Suppose that w>l.Then It is impossible.Thus where 1≤l≤2s+1?1,w≤l.Therefore,I is in Type 4. Next we study the structure of(1+v),(1+u+uv),(1+v+uv),(1+u+v),(1+u+v+uv)-constacyclic codes of length 2sover R.Similar to the discussion in Theorem 4.4,we have the following theorems. Theorem 4.5(1+u+uv),(1+u+v),(1+u+v+uv)-constacyclic codes over R are where a0j,a1j∈F2.Furthermore,f(x)is invertible if and only if a006=0. Now,Similar to the discussion in Theorem 4.4,we can complete the proof of statement. Theorem 4.6(1+v),(1+v+uv)-constacyclic codes over R are Now,in the proof of Theorem 4.4,we replace each v by u and get our statement.3 Cyclic and(1+uv)-Constacyclic Codes of Length 2sOver R
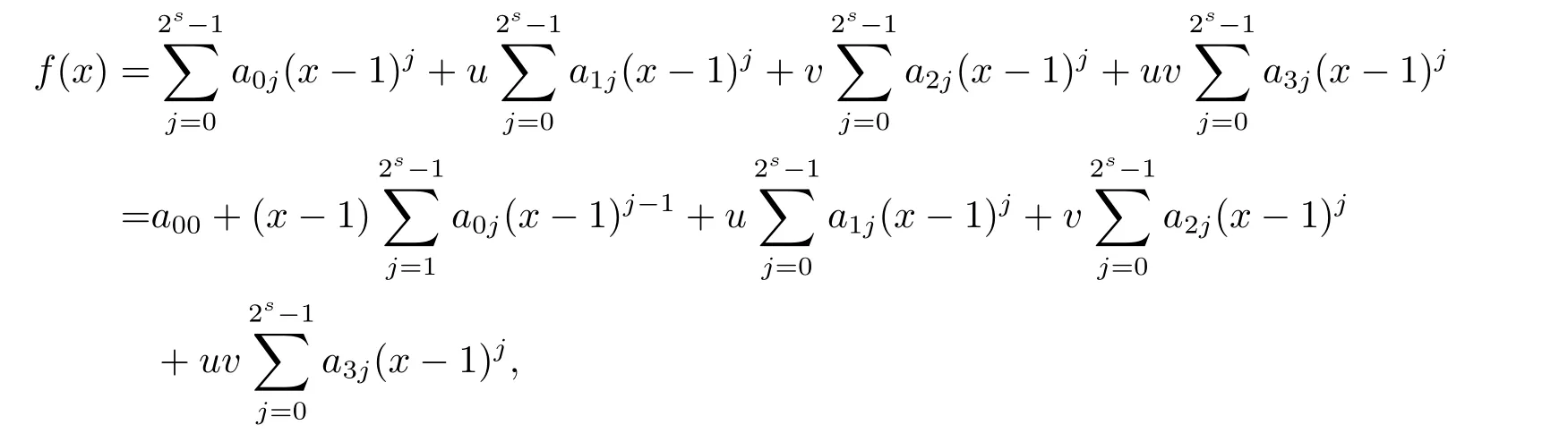
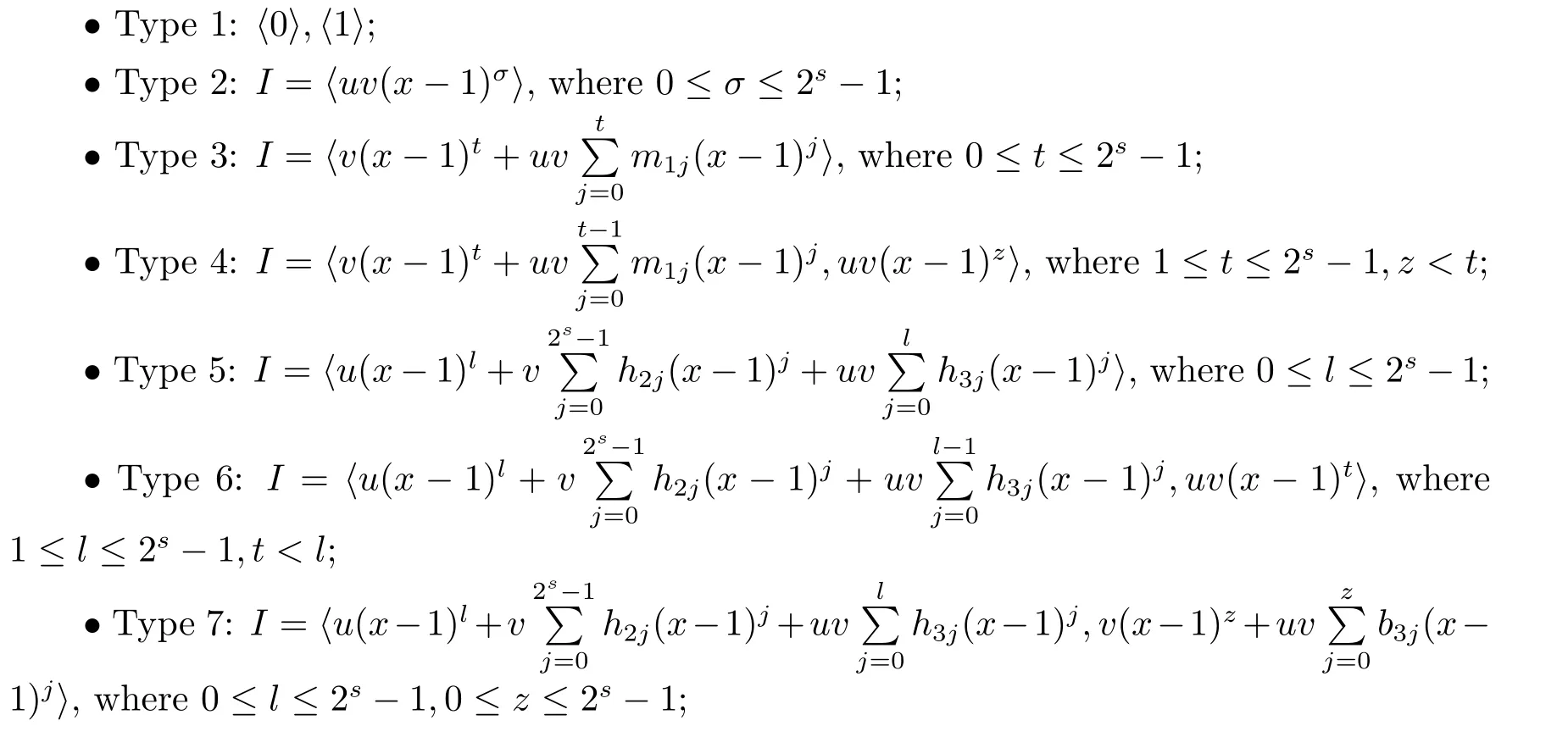

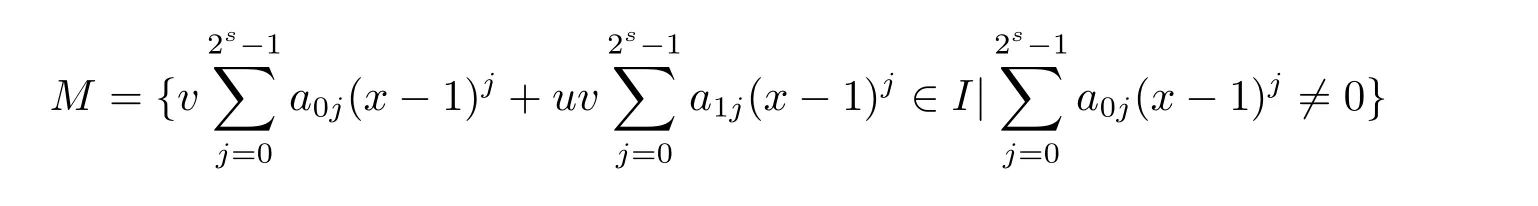
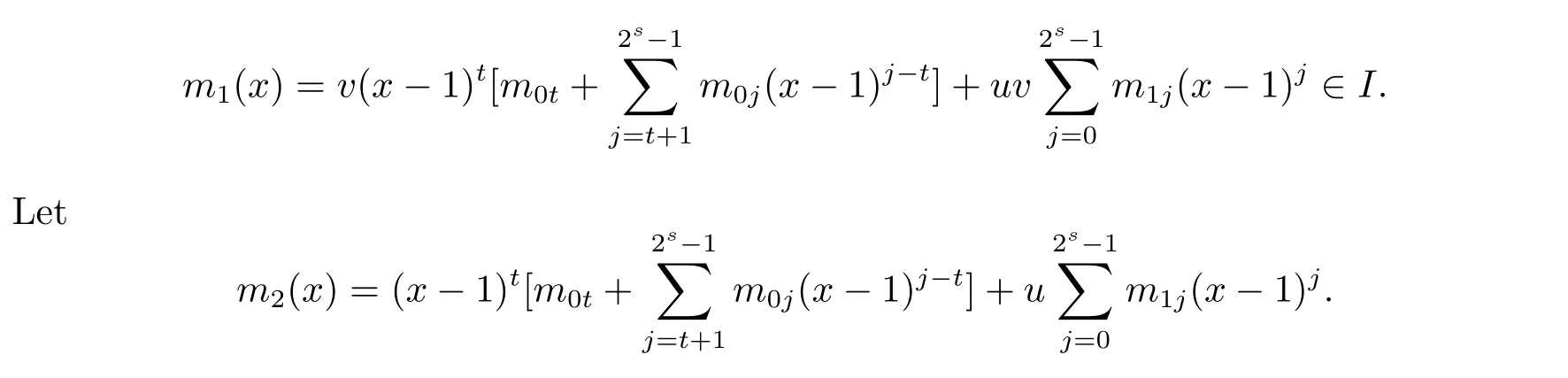
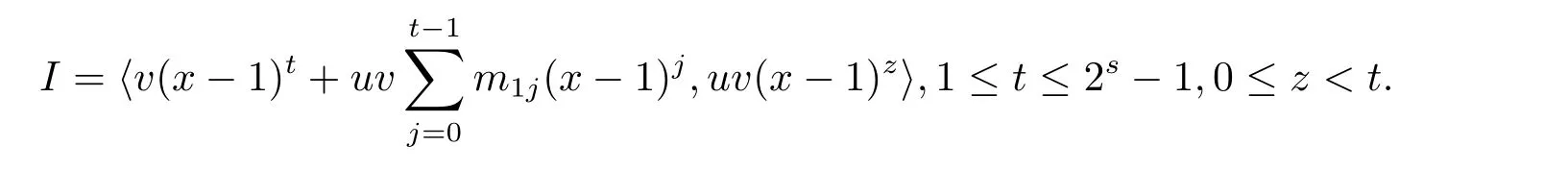
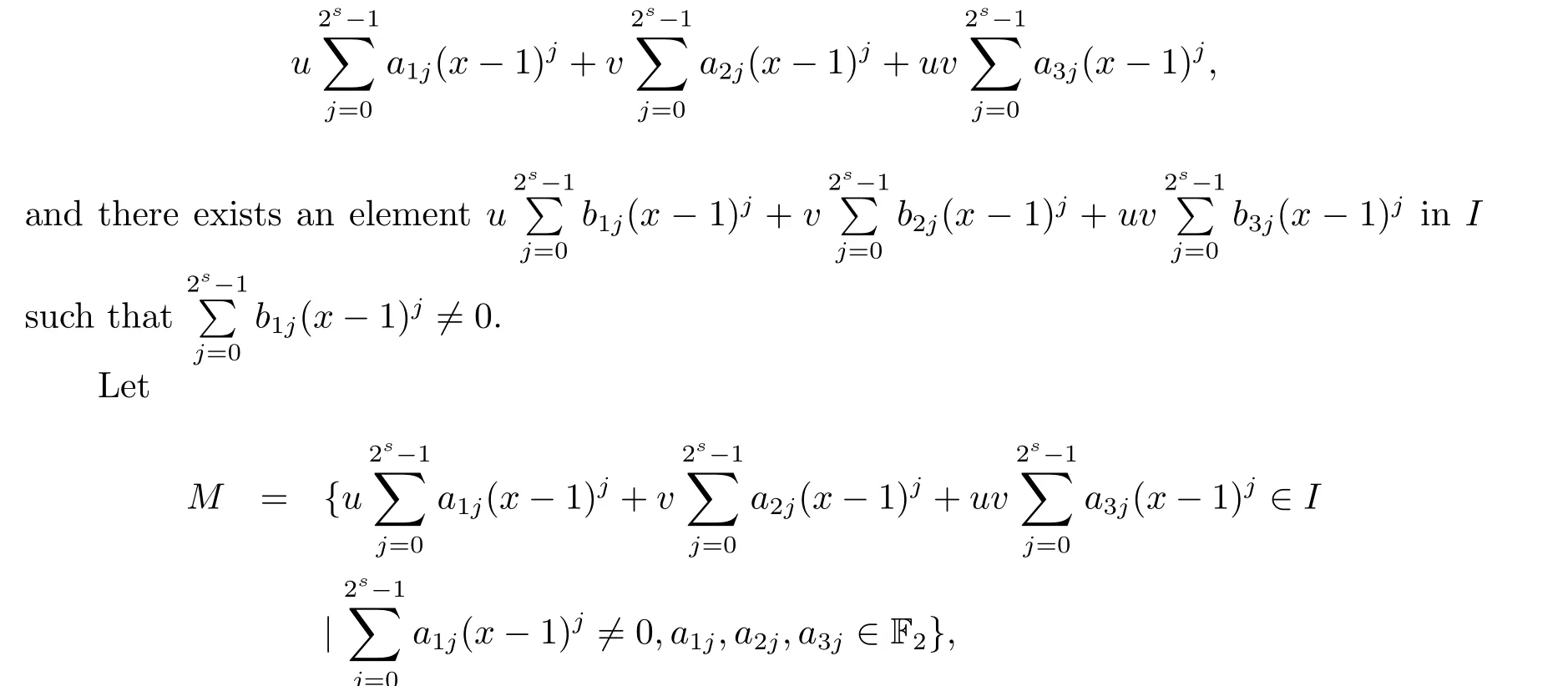

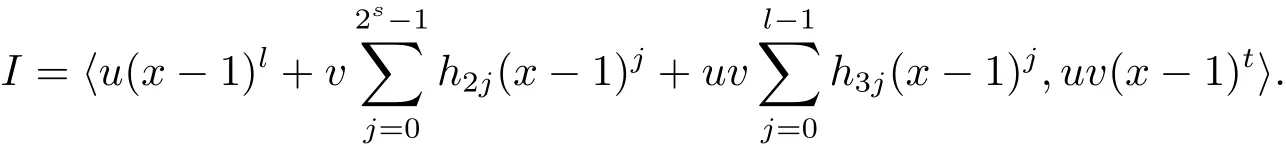
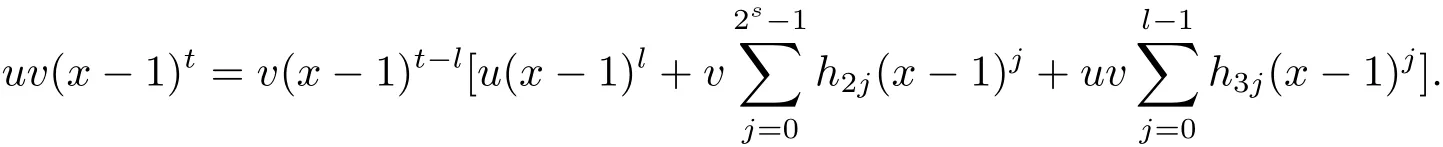
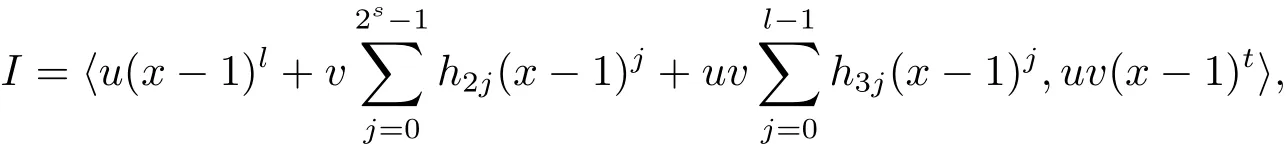
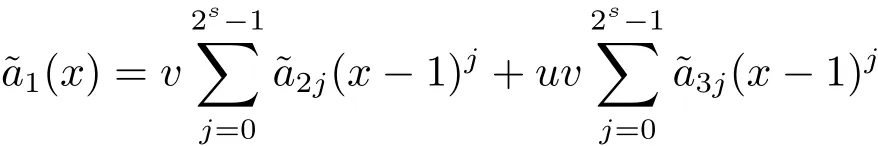
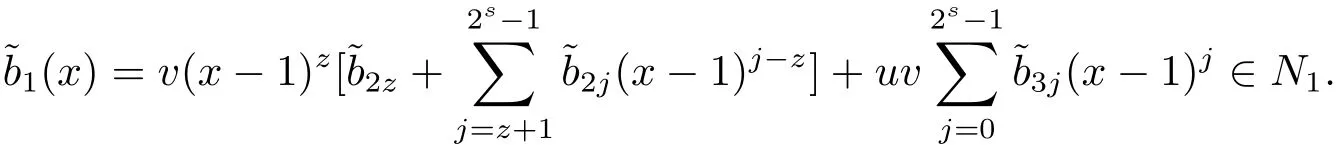
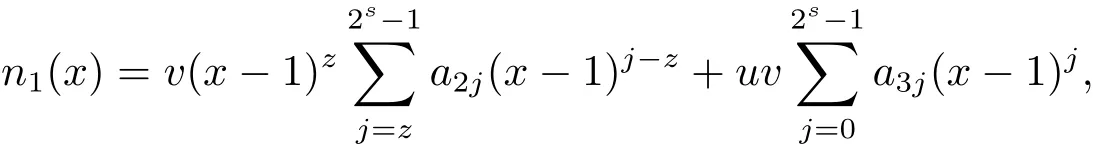
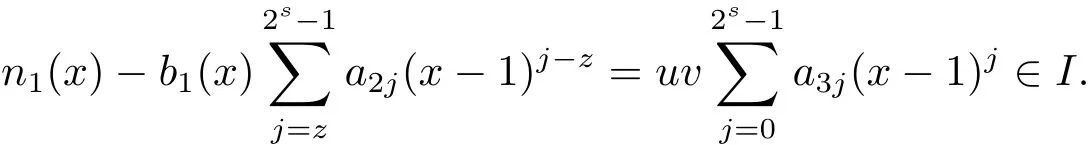
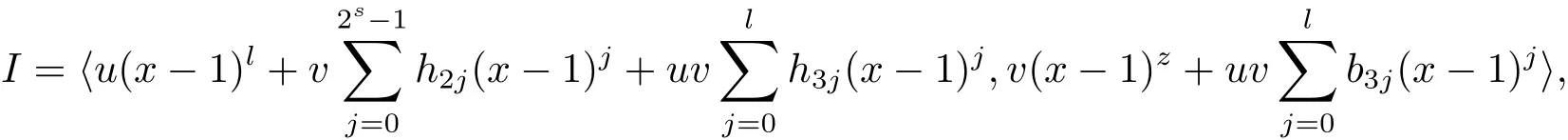
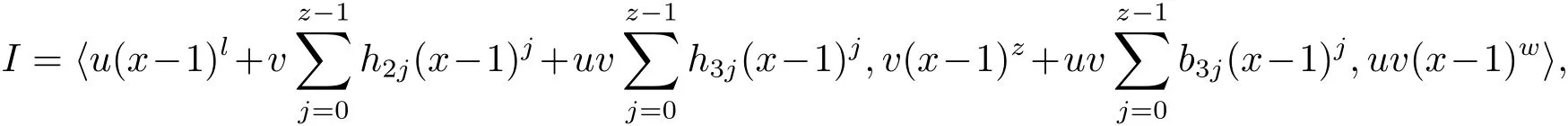
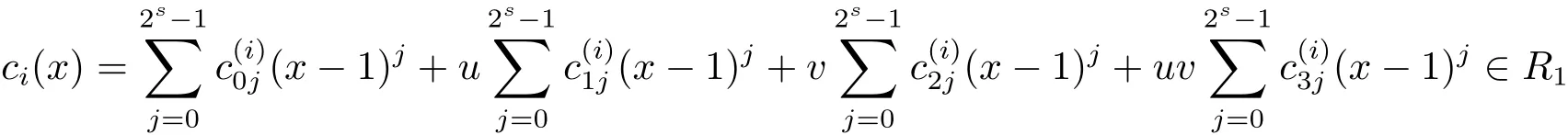
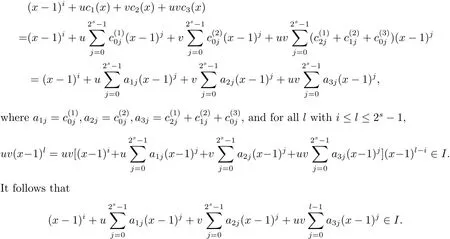
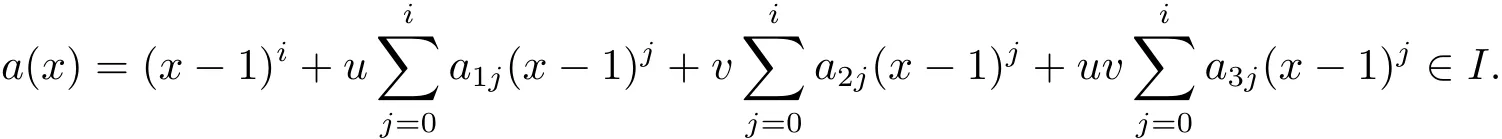
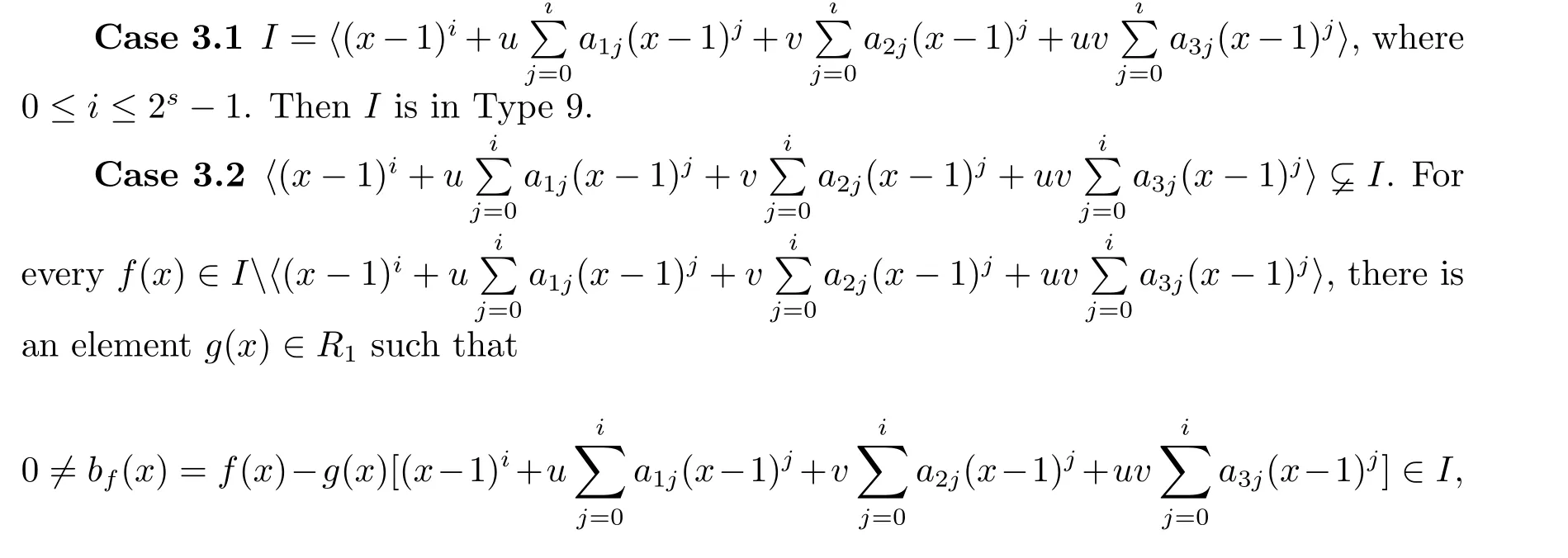
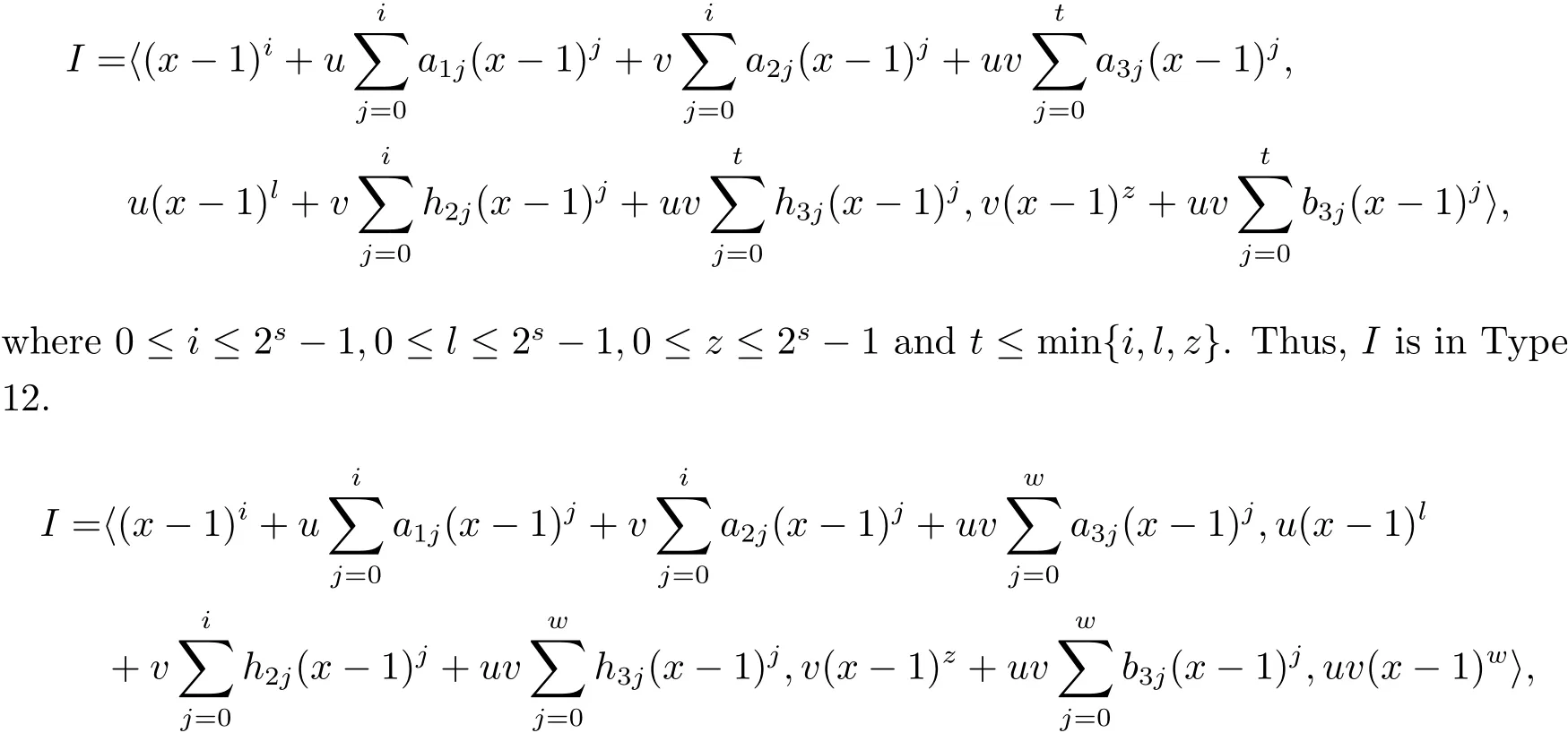

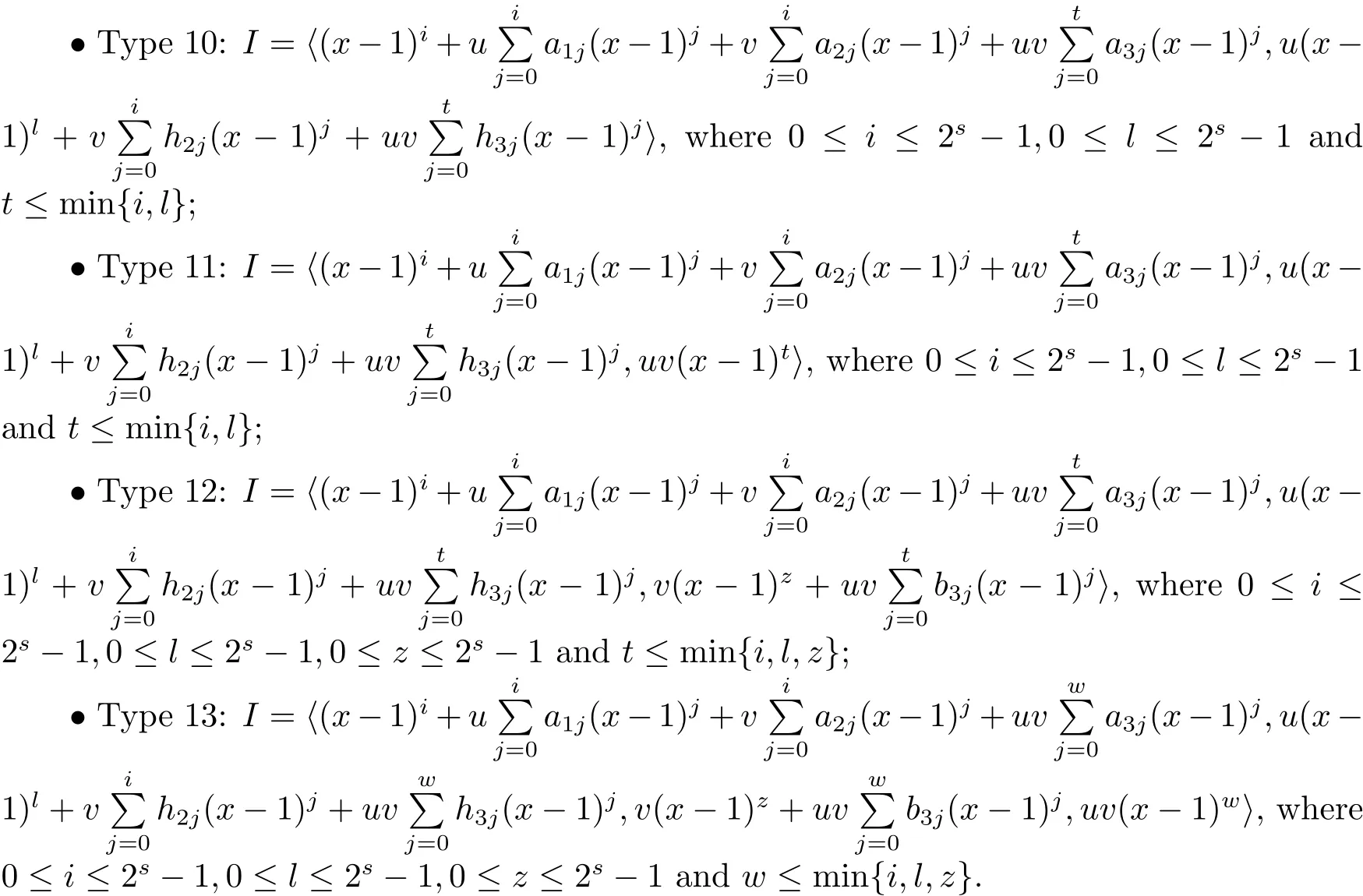
4 Constacyclic Codes of Length 2sover R