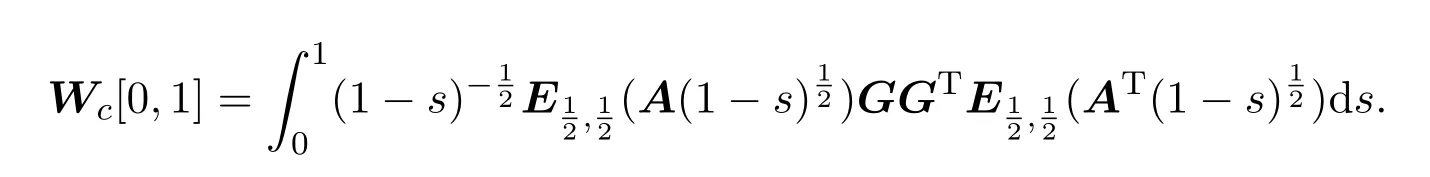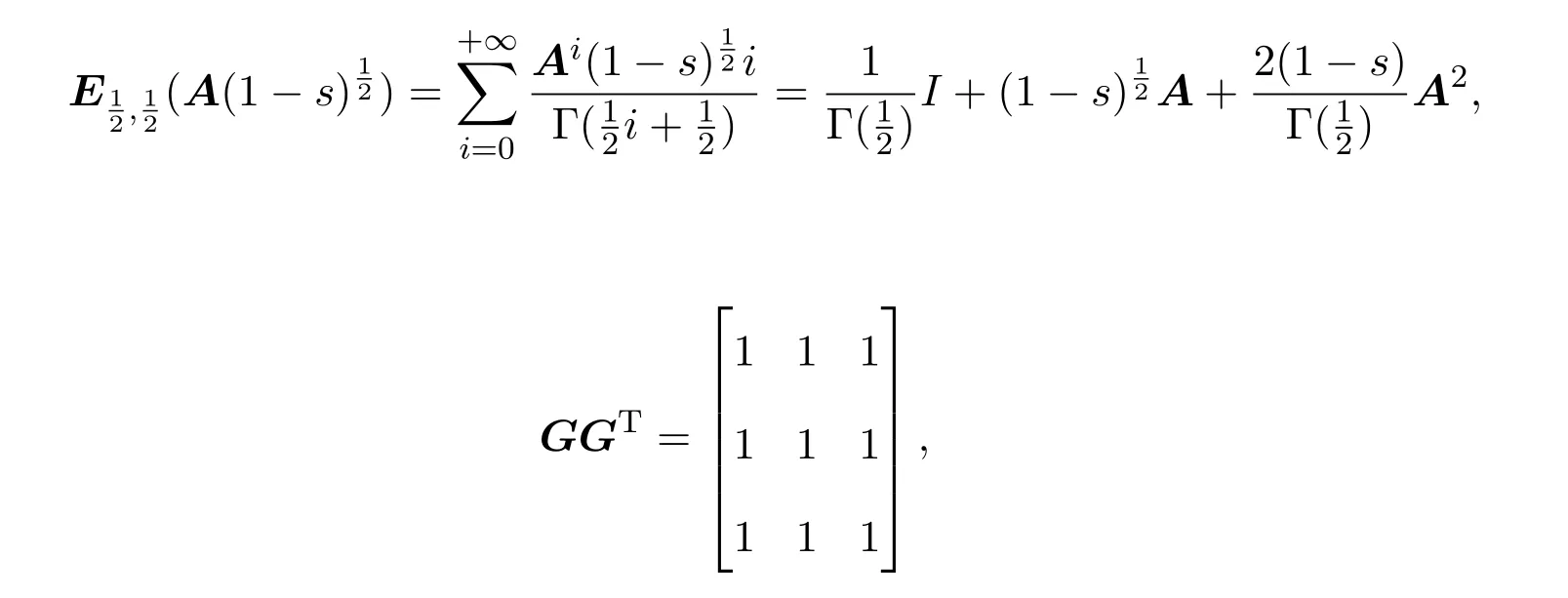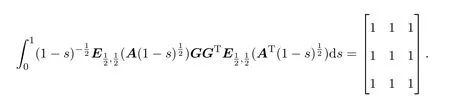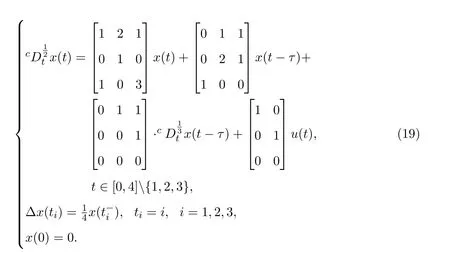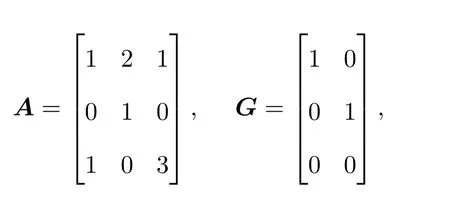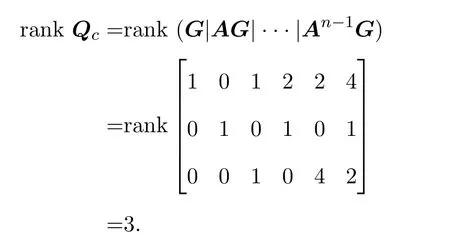Controllability of impulsive neutral control systems with different fractional orders
Li Nana
(School of Information and Network Engineering,Anhui Science and Technology University,Bengbu 233030,China)
Abstract:This paper is concerned with the controllability of a fractional linear timeinvariant impulsive neutral system.Our main purpose is to built some necessary and sufficient conditions of controllability for those systems.Two criteria on controllability of the system are established by constructing suitable control functions.Examples are given to illustrate our results.
Keywords:impulsive,neutral,controllability,fractional
1 Introduction
Fractional differential equatio ns have been proved to be one of the most effective tools in the modeling of many phenomena in various fields of physics,mechanics,chemistry,engineering,etc.With the development of theories of fractional differential equations,there has been a surge in the study of controllability of fractional differential systems[1-2].One of the main lemmas used in the study of controllability of fractional differential systems is the fixed point theorem[3].
In recent years,the problem of controllability for various kinds of fractional differential equations was extensively studied by many researchers.To our knowledge,the neutral impulsive fractional control systems have not been studied very extensively.The controllability of impulsive and neutral fractional dynamical systems have been investigated in references[2,4],respectively.The controllability of linear fractional dynamical systems have been studied extensively[5-7].As we know,it still has no paper to investigate the following systems:
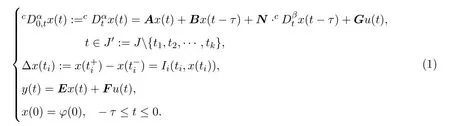
where
J∈[0,T],A,B,N∈Rn×n,G∈Rn×p,E∈Rk×n,F∈Rk×p,0<β<α<1,state variablex(t)∈Rn,initial function?(t)∈C([?τ,0],Rn),and control input
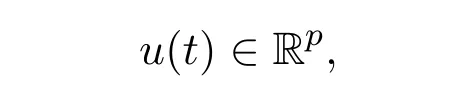
Ii:??→Rn,??J×Rn,T<+∞,i=1,2,···,k,represent the right and left limits ofx(t)att=ti,and the discontinuity pointst1 The structure of this paper is as follows.In Section 2,we brie fly present some basic notations and recall some concepts and preparation results.In Sections 3,some necessary and sufficient conditions of controllability for system(1)are given.At last,some examples are given to illustrate our results. In this section,we first recall some de finitions and lemmas. De finition2.1 The fractional integral of orderγwith lower limit zero for a functionf∈L1([0,∞))Rcan be written as provided the right side is point-wise de fined on[0,∞),where Γ(·)is the gamma function. De finition2.2 The Riemann-Liouville derivative of orderγwith the lower limit zero for a functionf:[0,∞)Rcan be written as De finition2.3 The Caputo derivative of orderγfor a functionf:[0,∞)?→Rcan be written as De finition2.4 The de finition of the two-parameter function of the Mittag-Leffler type is described by Remark2.1[10] (ii)Forβ=1,the matrix extension of the aforementioned Mittag-Leffler function has the following representation: Lemma2.1[11]Ifx(t)is a solution of system(1),we apply the Laplace transform for the system(1),then the solution of(1)is given by In this section,we discuss the controllability of system(1).At first,we give the de finition of controllability for system(1). De finition3.1[12]System(1)is said to be controllable if for every continuous initial function?,xtf∈Rn,there exists a controlu(t):[0,tf]?→Rmsuch that the corresponding solution of(1)satis fiesx(tf)=xtf. Next,we give a necessary and sufficient condition of controllability for system(1). Theorem3.1 System(1)is controllable on[0,tf]if and only if the controllability Gramian matrix is nonsingular for sometf∈(0,T],where·Tdenotes the matrix transpose. Proof Sufficiency.Suppose that the matrixWc[0,tf]is nonsingular,then its inverse is well-de fined.For anytf∈[0,t1],de fine the control function as We substitute(3)into(2)and lett=tf, By the De finition 3.1,the system(1)is controllable on[0,tf],tf∈[0,t1]. Fortf∈(t1,t2],de fine the control function as We substitute(5)into(2)and lett=tf, By the De finition 3.1,the system(1)is controllable on[0,tf],tf∈(t1,t2]. Moreover,fortf∈(ti,ti+1],i=1,2,···,k,de fine the control function as Substitutingt=tfin(2)and inserting(7),we have Thus the system(1)is controllable on[0,tf]. Necessity.Suppose system(1)is controllable.Now we prove that the matrixWc[0,tf]is singular.In fact,ifWc[0,tf]is singular,there exist a nonzero vectorz0such that that is it yields Since system(1)is controllable,there exist control inputsu1(t)andu2(t)such that and Subtracting(10)from(11)leads to Furthermore,multiplyingz0Ton the both sides of(12)we have Combining(9),we get the conclusionz0Tz0=0.This contraction therefore completes the proof. Theorem 3.1 is a geometric type condition;by simple transformation,we can get an algebraic type condition. Theorem3.2 The system(1)is controllable on[0,tf]if and only if ProofWith Cayley-Hamilton theorem,tα?1Eα,α(Atα)can be written in the following form: Fortf∈[0,t1], Denote the vectorβas Subtracting(13)from(14),we can obtain where Note that,sincextf,x0are arbitrary,to have a unique solution ofu(t),the necessary and sufficient condition is clearly that Denote the vectorγas Subtracting(16)from(17),we can obtain Note that,sincextf,x0are arbitrary,to have a unique solution ofu(t),the necessary and sufficient condition is clearly that In this section,we consider an example of linear time-invariant impulsive neutral control systems with different fractional orders to demonstrate how to utilize our results. Example4.1 Consider system(1).We choose,and Now we apply Theorem 3.1 to prove system(1)is controllable.First, By computation,we obtain and We can get that the matrixWc[0,1]is nonsingular.Thus,the system(1)is controllable. Example4.2 Consider the following 3-dimensional impulsive neutral fractional system Now,we try to use our criteria to investigate the controllability on[0,4]of system(19).Denote by then,one can obtain By Theorem 3.1,the system(19)is controllable on[0,4].2 Preliminaries
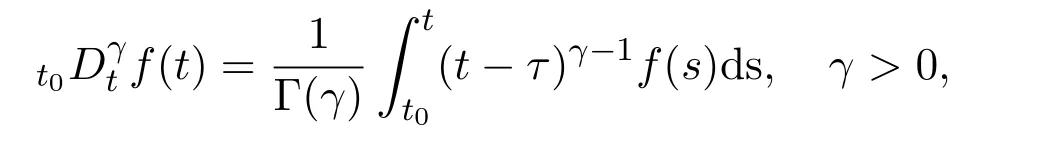
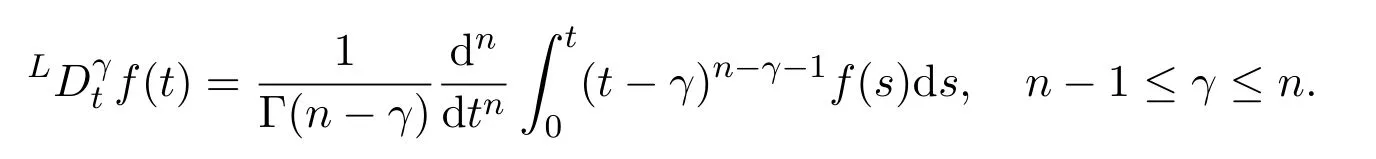

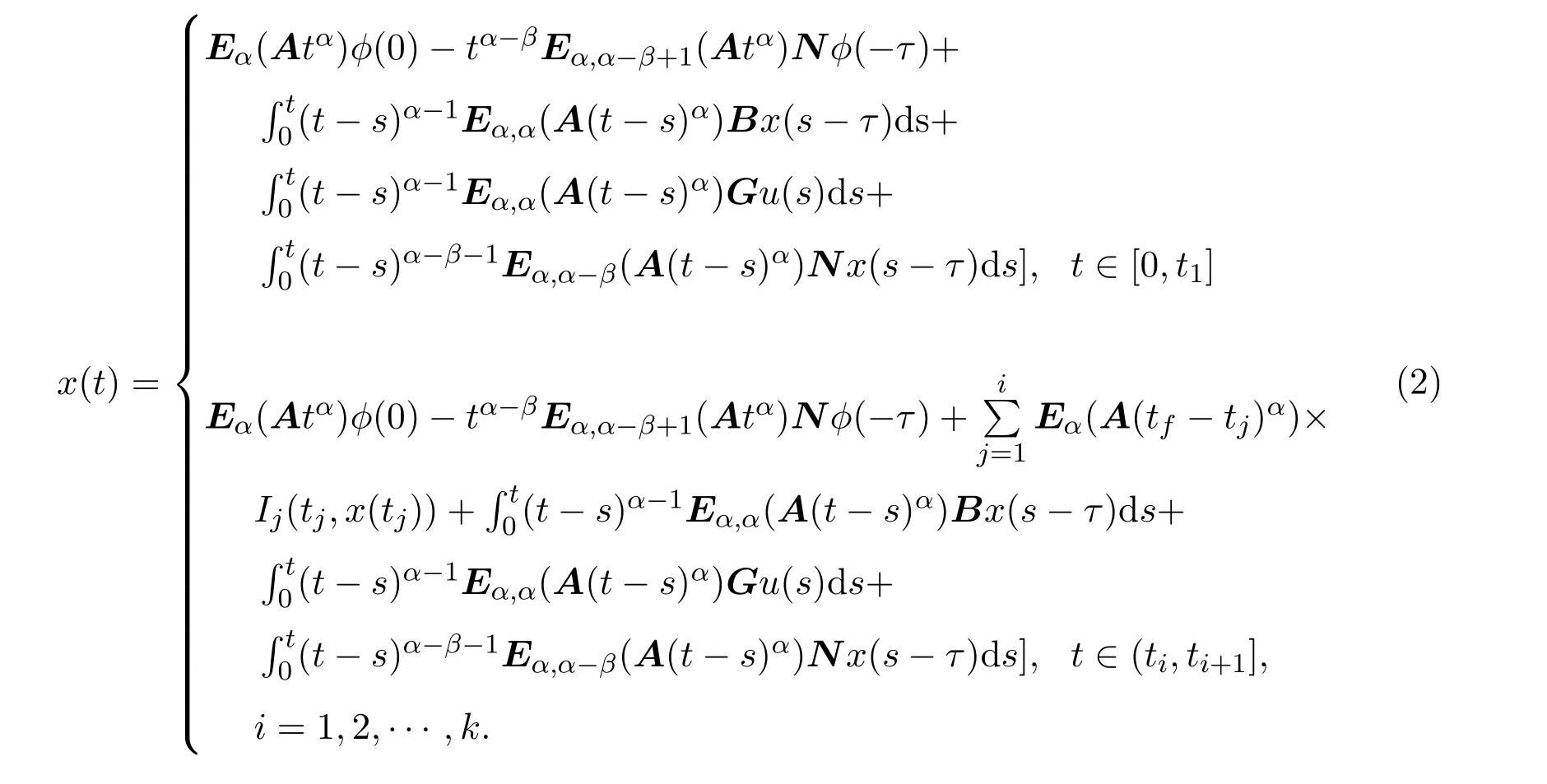
3 Main results
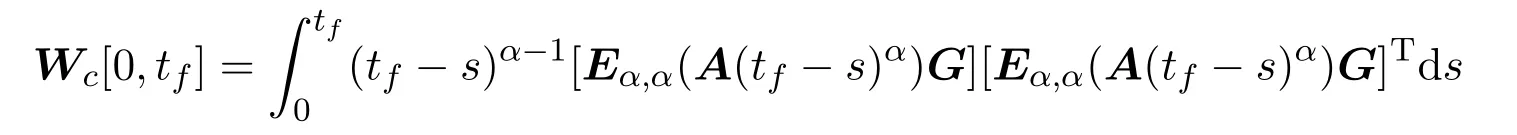
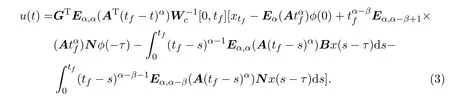
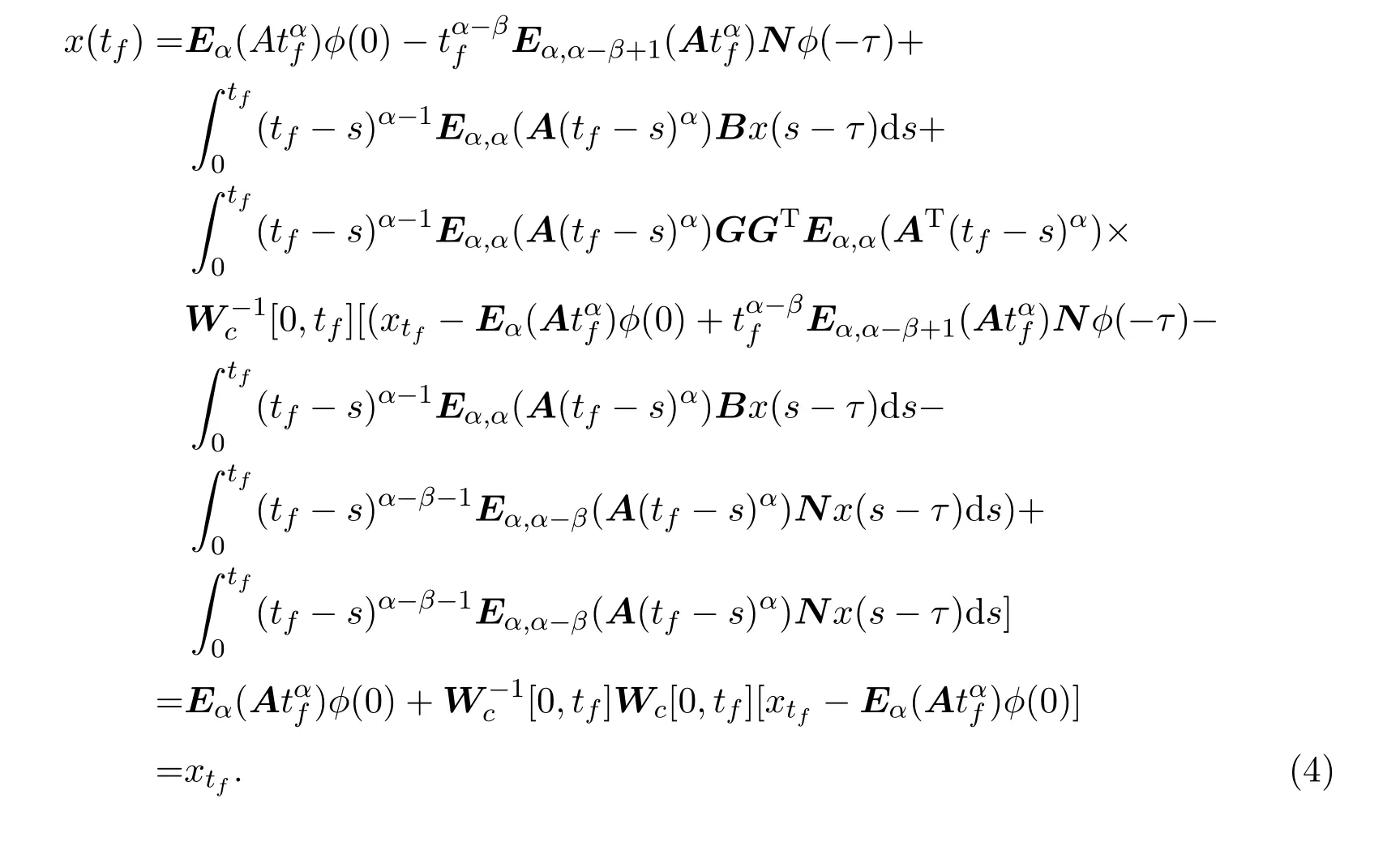

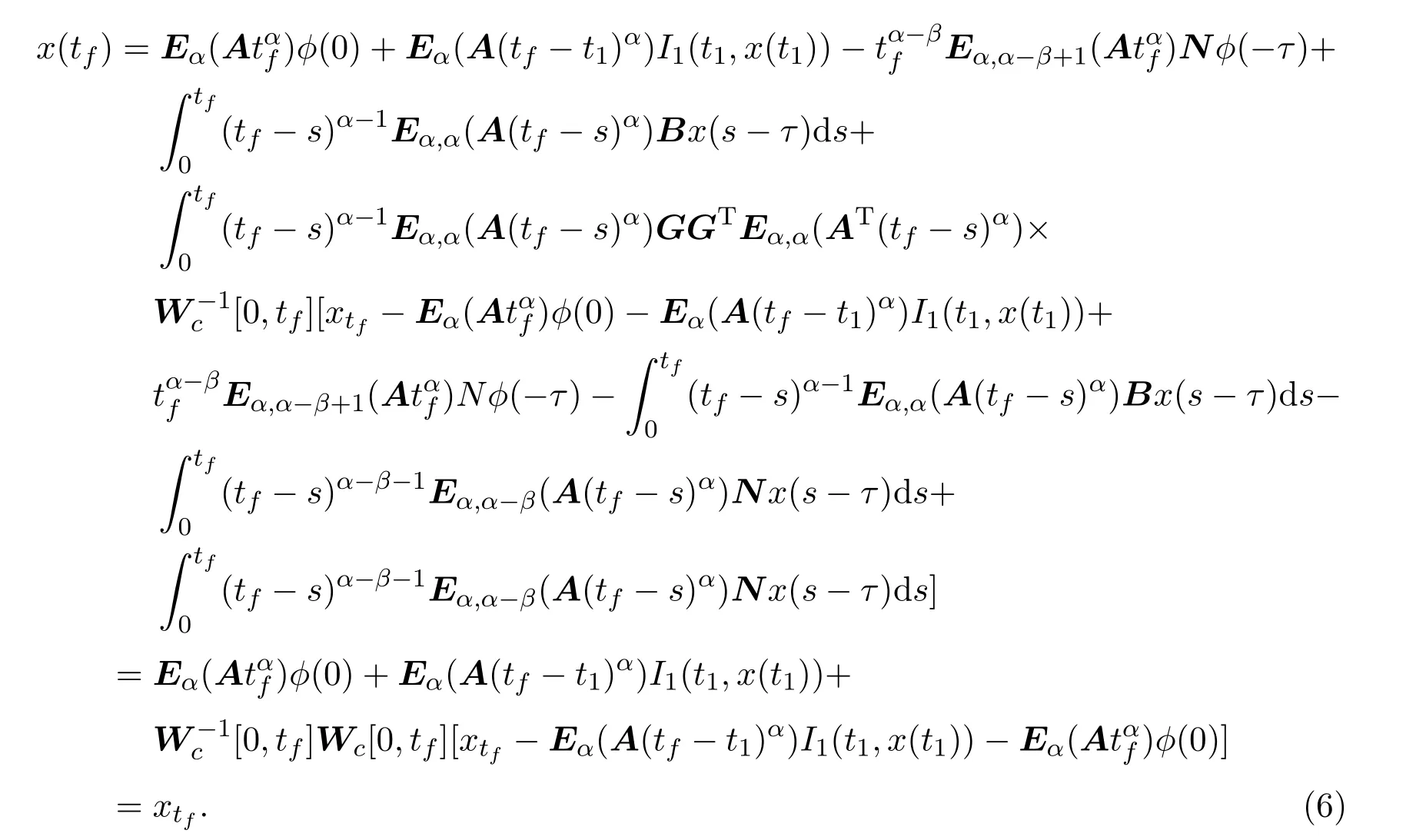
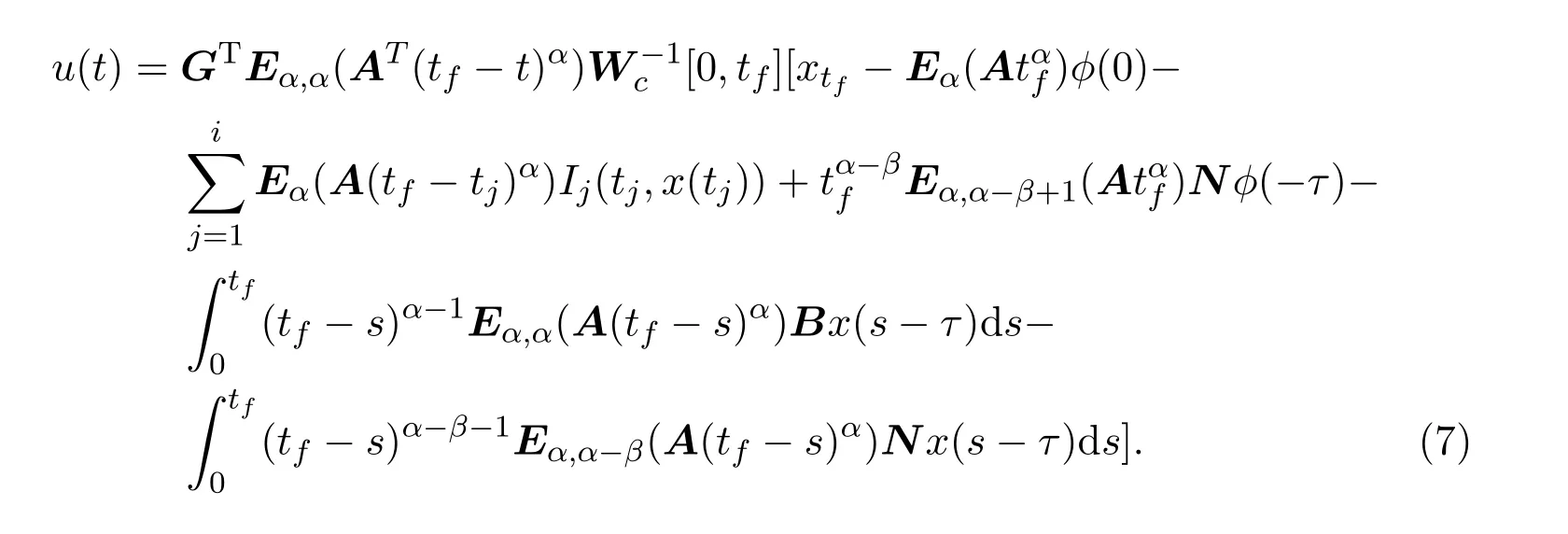
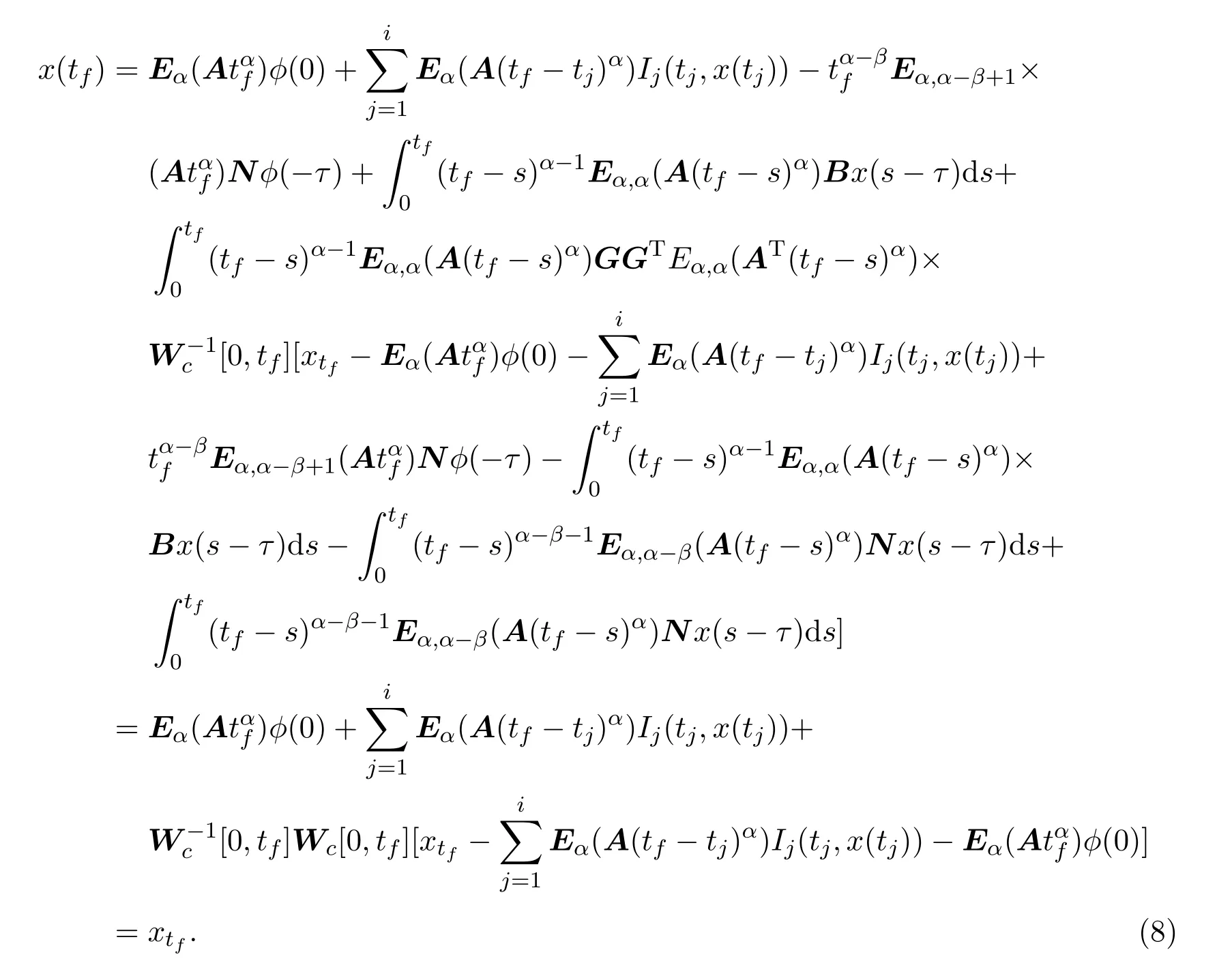
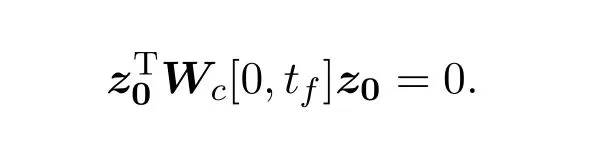



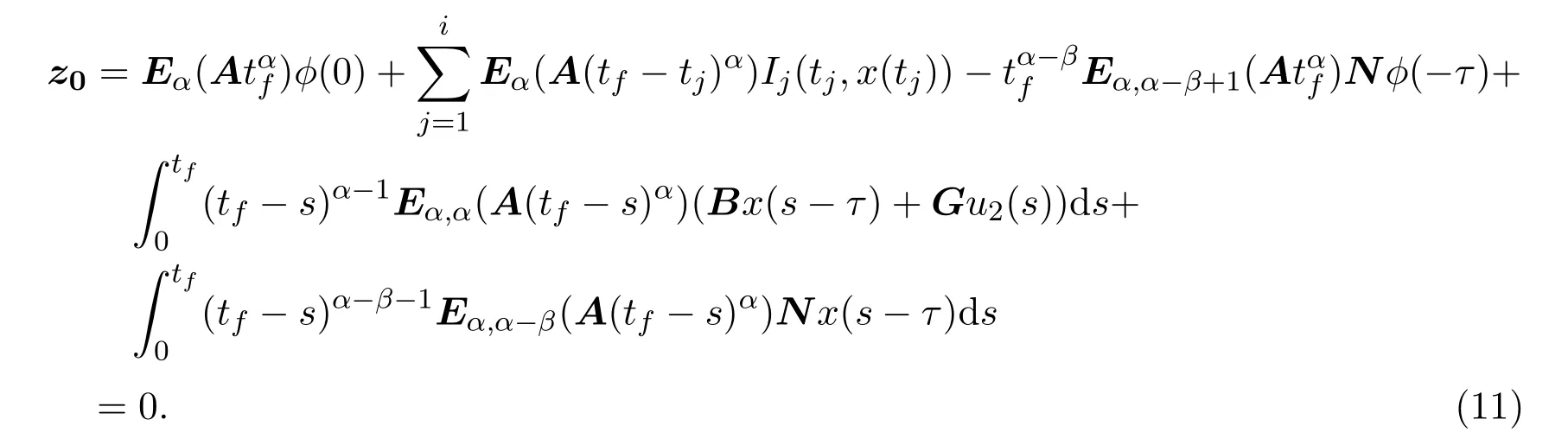


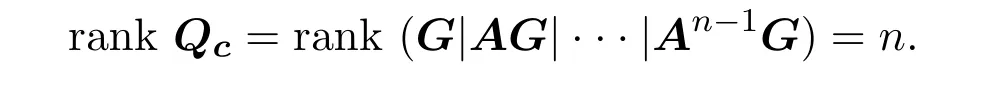

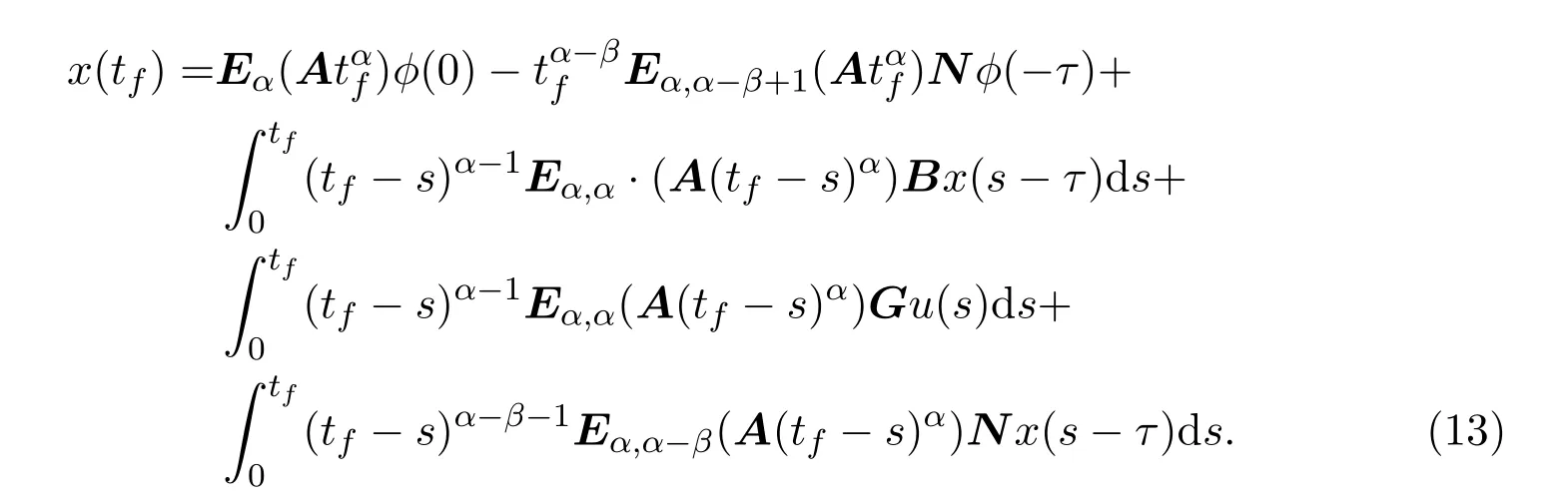
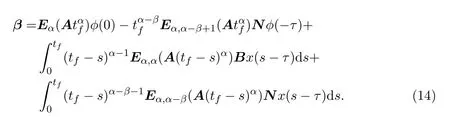
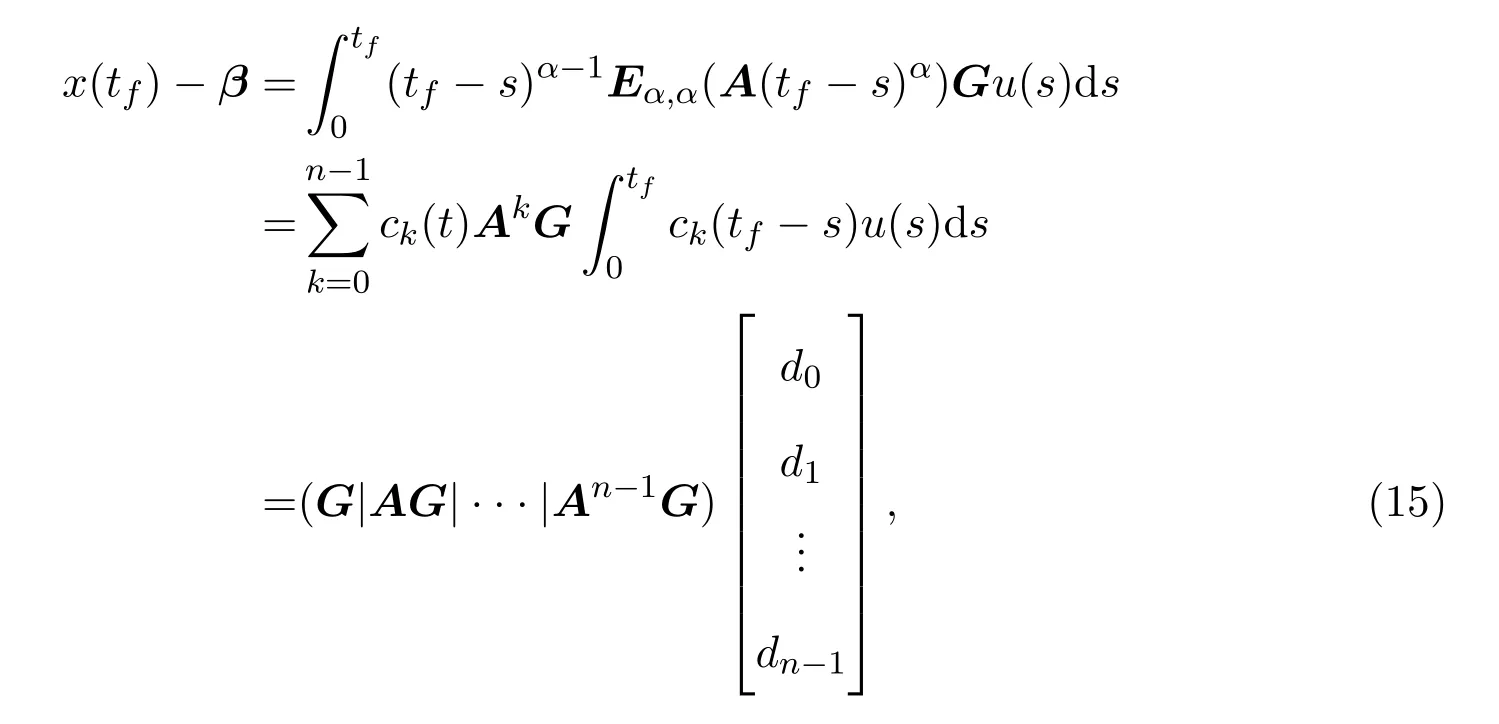
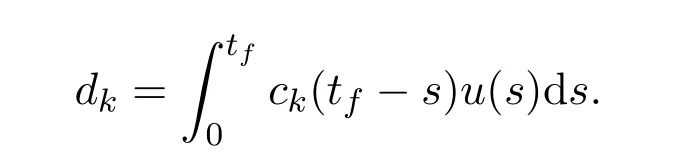

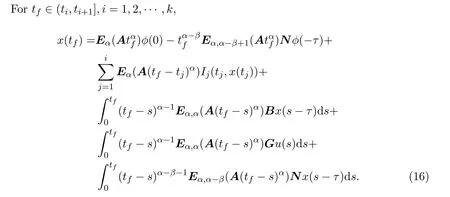
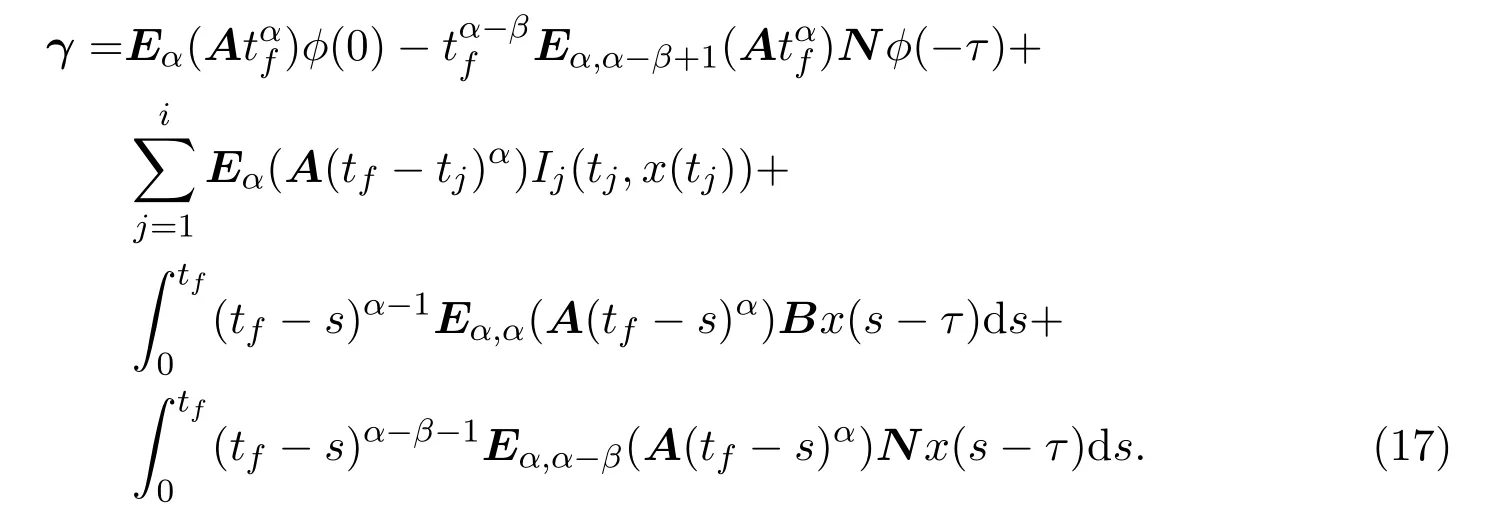
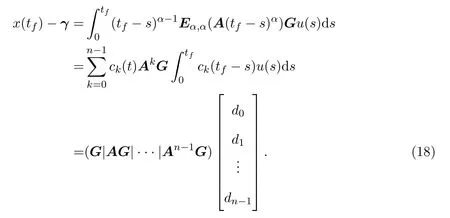

4 Illustrate examples