Ya Meng,Yi Fang,Chuan Zhang,Liping Li,

1 Key Laboratory of Intelligent Computing and Signal Processing of the Ministry of Education of China,Anhui University,Hefei 230031,China

2 School of Information Engineering,Guangdong University of Technology,Guangzhou 510006,China

3 National Mobile Communications Research Laboratory,Southeast University,Nanjing,China

Abstract: This paper studies the decoding performance of low-density parity-check (LDPC)codes in a serial concatenation system with polar codes employing the successive cancellation (SC) decoding.It is known that the absolute incorrect log-likelihood ratio (LLR) values from the SC decoding can be very large.This phenomenon dramatically deteriorates the error correcting performance of the outer LDPC codes.In this paper,the LLR values of polar codes are regulated by a log processing before being sent to the LDPC decoder.Simulation results show that the log processing is an efficient approach with a low optimization complexity compared with the existing procedures to improve the performance of the serial concatenation systems.

Keywords: polar codes; SC decoding; LDPC codes; concatenation.

I.INTRODUCTION

POLAR codes,which were first proposed by Ar?kan in [1],can achieve the channel capacity over any symmetric binary-input discrete memoryless channels (B-DMCs) with low encoding and decoding complexity.

Concatenations of polar codes with other coding schemes are often explored to provide powerful error-correcting capability [2],[3].The concatenation of an inner LDPC code with an outer polar code was investigated in[4],where polar codes were used to remedy the error floor of LDPC codes.In [5],concatenations of polar codes with outer non-binary LDPC codes were studied to improve the performance of finite-length polar codes.Applying belief propagation (BP) decoding to polar codes,the concatenation scheme with an outer LDPC code was investigated in [6],where a set of encoded bits of a polar code is selected to be protected by an outer LDPC code.The work in [7]investigates the dependence among the information bit errors and proposes to break the dependence through an outer LDPC code.However,the aforementioned concatenation systems do not consider the effect of the large LLR values from the polar decoder (i.e.,the SC decoder) over the decoding performance of the outer LDPC codes.

Considering the negative impact of large incorrect LLRs from the SC decoding,the concatenation scheme of a LDPC code with a polar code is studied in this paper.To simplify the exposition,denote the direct concatenation of an outer LDPC code with an inner polar code as LDPC+POLAR.Similarly,POLAR+LDPC indicates the concatenation of an inner LDPC with an outer polar code.Due to the hard decisions of previous decoded bits being utilized in the subsequent steps of the SC decoding,the incorrect absolute values of LLRs tend to be very large.When the inner code is a LDPC code with the BP decoding,the LLR values are normal since no hard decisions are employed in the decoding process.Therefore,the performance of the LDPC+POLAR concatenated system can be worse than that of the POLAR+LDPC system.This phenomenon is studied and shown in this paper.

In this paper,the LLR distribution from the SC decoding is studied to show the impact of the large absolute values of LLRs on the concatenation systems.

This paper also tries to improve the performance of the LDPC+POLAR concatenation scheme.Specifically,a deeper investigation of the LLR distribution from the SC decoder is presented.As in [8],[9],the LLR from the SC decoder goes through a Cauchy processing and a clipping processing,which are originally proposed to improve the performance of LDPC codes over impulsive channels.Limited by the complicated nature of the Cauchy processing and the sub-optimality of the clipping processing,a log processing of the LLRs from the SC decoder is proposed in the paper.With the log-processed LLR values fed to the LDPC decoder,the concatenation system shows a better performance than both Cauchy and clipping processing.For any block error rate (BLER) below 10-3,the LDPC+POLAR concatenation system with the log processing outperforms the POLAR+LDPC concatenation system.At a bit-error-rate (BER) =10-4,the LDPC+POLAR concatenation system with the log processing has 1 dB gain over the LDPC+POLAR systems without any LLR processing.At a BER =10-5,the LDPC+POLAR concatenation system with the log processing has 0.4 and 0.2 dB gains over the LDPC+POLAR systems with the clipping scheme and with the Cauchy processing,respectively.Additionally,compared with the clipping and Cauchy processing schemes,the proposed log processing helps to accelerate the convergence speed of the outer LDPC decoder in such concatenation systems.

The rest of the paper is organized as follows.Section II introduces the fundamentals of polar codes.The log processing method is introduced in section III.Section IV presents the simulation results.The conclusion remarks are provided at the end.

II.PRELIMINARIES

In this section,polar codes in [1]and the SC decoding algorithm are brief l y reviewed.The original concatenation system of an inner polar code with an outer LDPC code without the log processing scheme is introduced.

2.1 Polar codes

LetW:XY→ denote a B-DMC,where X={0,1} is the input and Y is the output alphabet.Its transition probability is denoted asW (y|x),withx∈X andy∈Y.

The generator matrix for polar codes isGN=BN F?n,whereBNis a bit-reversal matrix,andF?nis thenth Kronecker power ofFover the binary field F2.A codewordcan be generated throughwhere the source vectorconsists of the information bits and the frozen bits,denoted byuAand,respectively.The set A can be constructed by selecting indices of the bit channels with the smallest Bhattacharyya parameter in BEC channels.For all the other channels,construction procedures can be found in [10]-[13].

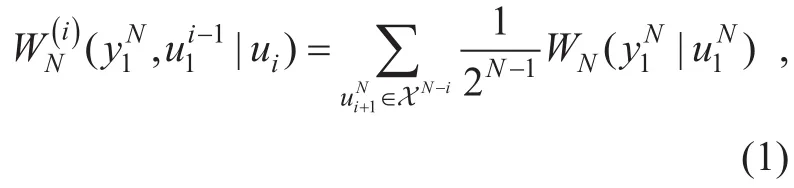
where

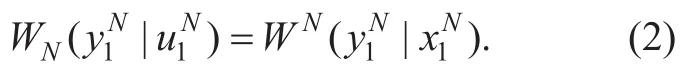
2.2 SC decoding of polar codes

SC decoding proposed in [1]is the basic decoding algorithm of polar codes.For eachui(i∈A),the likelihood ratio (LR) can be calculated as

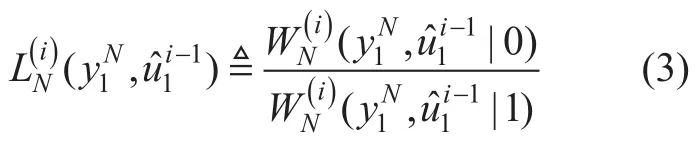
and the decision is made as

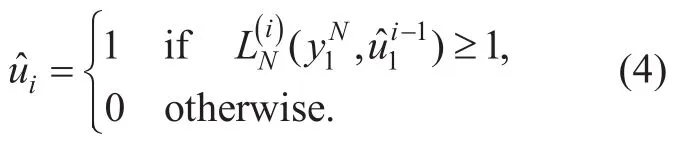
The frozen bits are known to both the transmitter and the receiver.Therefore,ifthenA straightforward calculation using the recursive formulas in [1]is given as

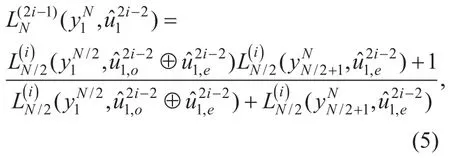
and

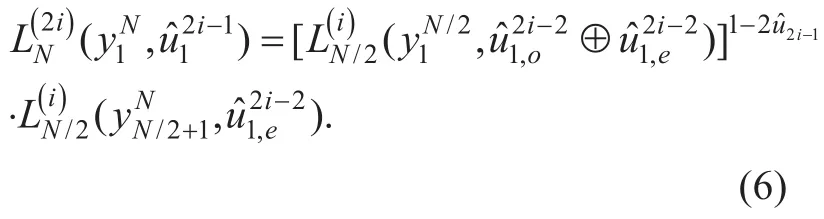
After the SC decoding of polar codes,we obtain the LLR values of polar codes by

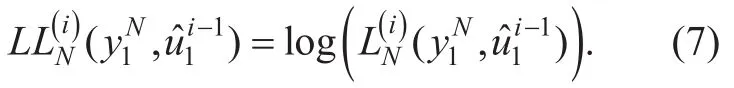
2.3 Concatenation scheme

The concatenation system of an inner polar code with an outer LDPC code is introduced here.The concatenation system considered in this paper is a simple serial concatenation system without interleaving,as shown in figure 1.

LetKlbe the number of information bits to be encoded in a LDPC block with a block lengthNl.For ease of description,let us assumeNlis a multiple ofK(Kis the information bit length of polar codes).The structure does not change whenNlis not a multiple ofK.After the LDPC encoder,a codeword of lengthNlis passed to the polar encoder.One LDPC codeword is divided intoNl/Kpolar

III.LOG PROCESSING OF THE LLR

In this section,we first analyze the LLR distribution of polar codes from the SC decoding.Then the log processing is proposed.

3.1 LLR distribution

The cumulative distribution function (CDF) of the LLRs from the SC decoding is presented in figure 2-(a).The polar code has the block lengthN=256 and the information bit lengthK=64.The simulated SNR isEb/N0=8 dB.The solid line is the CDF of LLRs collected from the correct code blocks.The dashed line is the CDF of LLRs collected from the incorrect blocks.Here all zeros are transmitted,expecting correct LLR values to be larger than zero.It can be observed from figure 2-(a) that both the correct and the incorrect polar blocks have very large absolute values of LLRs.The very large incorrect LLR values are likely not to be corrected in the decoding process,which results in decoding errors [14].In a LDPC+POLAR concatenation system,the output blocks,then yieldingNK l/ polar codewords of lengthN.These codewords are then modulated (by binary phase shift keying,BPSK)and sent through the underlying channelW.In the receiver side,the received samplesof one polar block are fed into the polar decoder.Then,the LLR values forKinformation bits are extracted.StackingKLLRs fromNKl/polar blocks forms the input of the LDPC decoder.Finally,theKlinformation bits can be estimated.LLR values of polar blocks are fed to the BP decoder of LDPC codes.

Fig.1.The serial concatenation scheme of the LDPC code as the outer code and the polar code as the inner code.

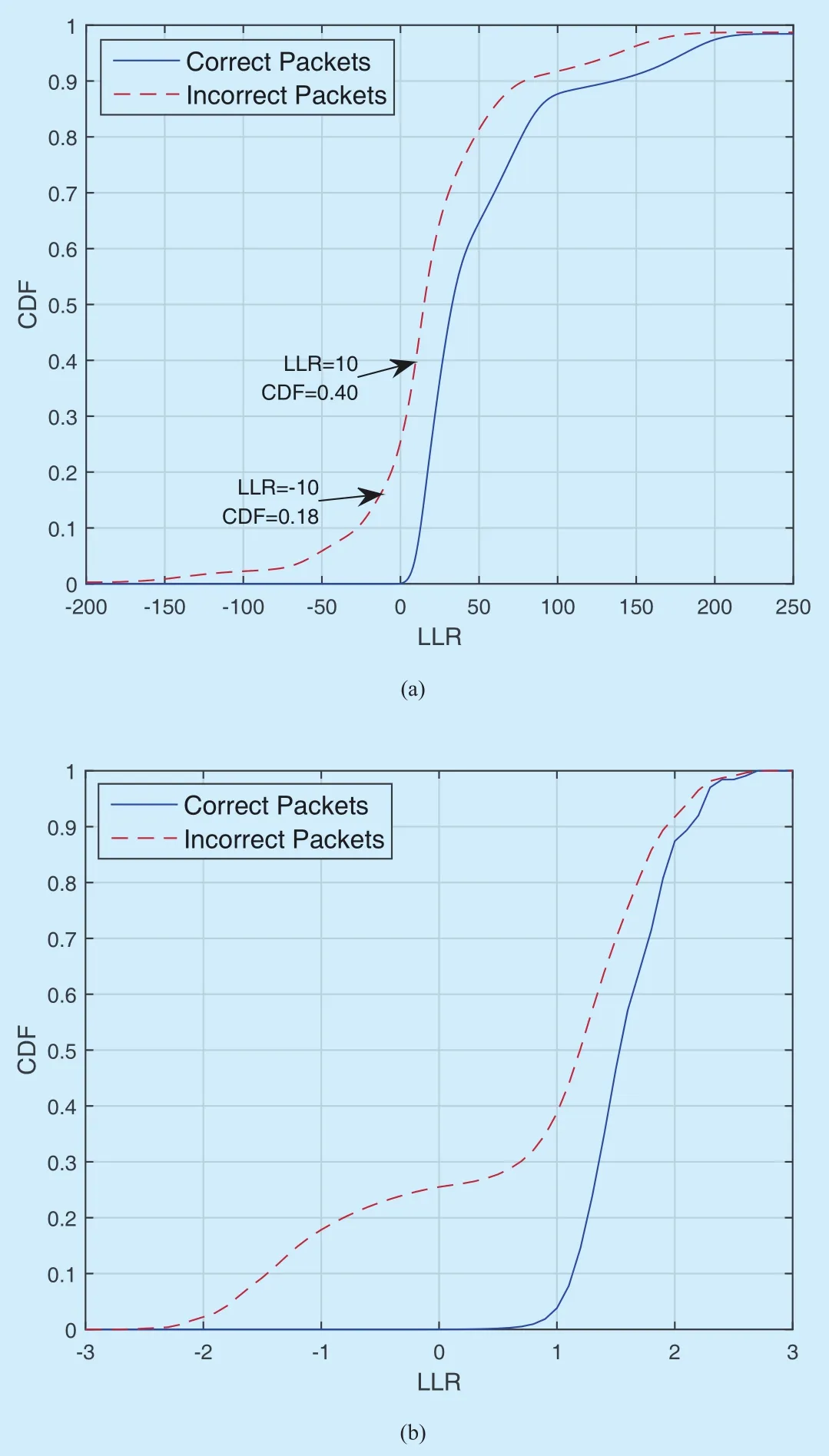
Fig.2.The CDF of the LLRs from the SC decoding of (a) without the log processing and (b) with the log processing.The block length of the polar code is N=256,and the code rate is R=1/4.The simulated SNR is Eb/ N0=8 dB.

Large incorrect absolute values of LLRs result in large probability of incorrect decisions for the BP decoder.For example,there are 18% of large incorrect absolute LLR values (larger than 10) from the incorrect polar blocks,indicating that there are 0.18Knodes with large incorrect absolute values of LLRs at the input to the LDPC decoder even when there is only one incorrect polar block.Although it is hard to theoretically come up an expression on the probability of the BP decoding failure,it can be observed in the sequel that the error performance is largely deteriorated by these extreme incorrect LLRs.Great improvement is observed by regulating the LLR values from the SC decoder.

3.2 Cauchy processing and clipping processing

Inspired by the work in [8],[9]where the impulsive noise is treated to follow a Cauchy distribution,the heavy-tailed LLRs from the SC decoding can be treated the same way: random variables following a Cauchy distribution.DenoteLas such a random variable withL(x0,γ),wherex0is the location parameter,andγis the scale parameter of the Cauchy distribution.The LLR going to the LDPC decoder is re-calculated as:

The parameters of this Cauchy distribution need to be estimated from the observed LLR values of the SC decoder.Thus,the Cauchy processing is complicated and the following clipping method is an alternative approach with a relatively low complexity.

First let us define a sign function.For a given variablex,a sign function is expressed as

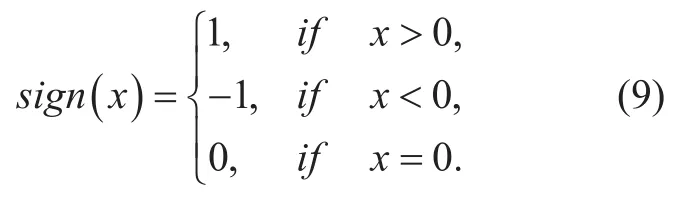
Therefore,for theith LLR valueLi,the clipping scheme works as follows:

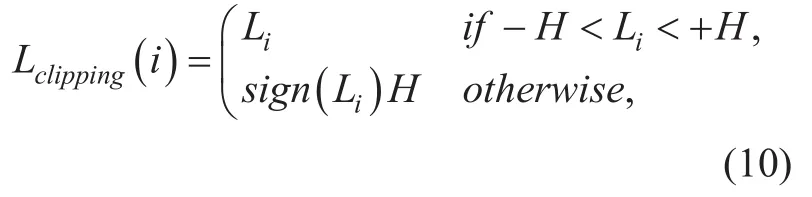
whereHis an optimal threshold that needs to be optimized,for example,from empirical studies.

3.3 Log processing of LLRs

As discussed,the Cauchy processing is com-plicated because of the unknown parameters.The clipping scheme limits everything beyond the threshold to be the same,which is obviously not optimal.In this paper,we propose a log processing of the LLR values from the SC decoding,which is shown to be an effective processing for the LLR values with unknown features.Since the log processing does not require any features of the LLR values,it is therefore simpler compared to the Cauchy processing.

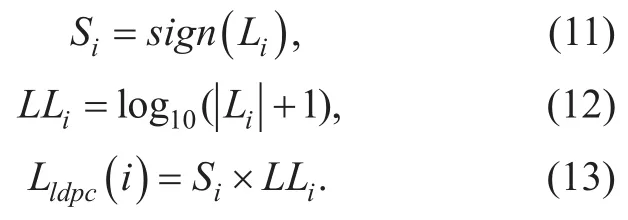
IV.SIMULATION RESULTS

In this section,simulation results are provided to verify the improved performance of the concatenation system with the log processing.The LDPC code simulated in this section is the(256,64) MacKay code [15]where the code length isNl=256,and the length of information bits isKl=64.The maximum number of BP decoding iterations is 50.The polar code also has a code lengthN=256 and the information lengthK=64,which is constructed according to Tal-Vardy’s procedure [10]for each simulatedEb/N0.The underlying channel in this simulation is the AWGN channel.

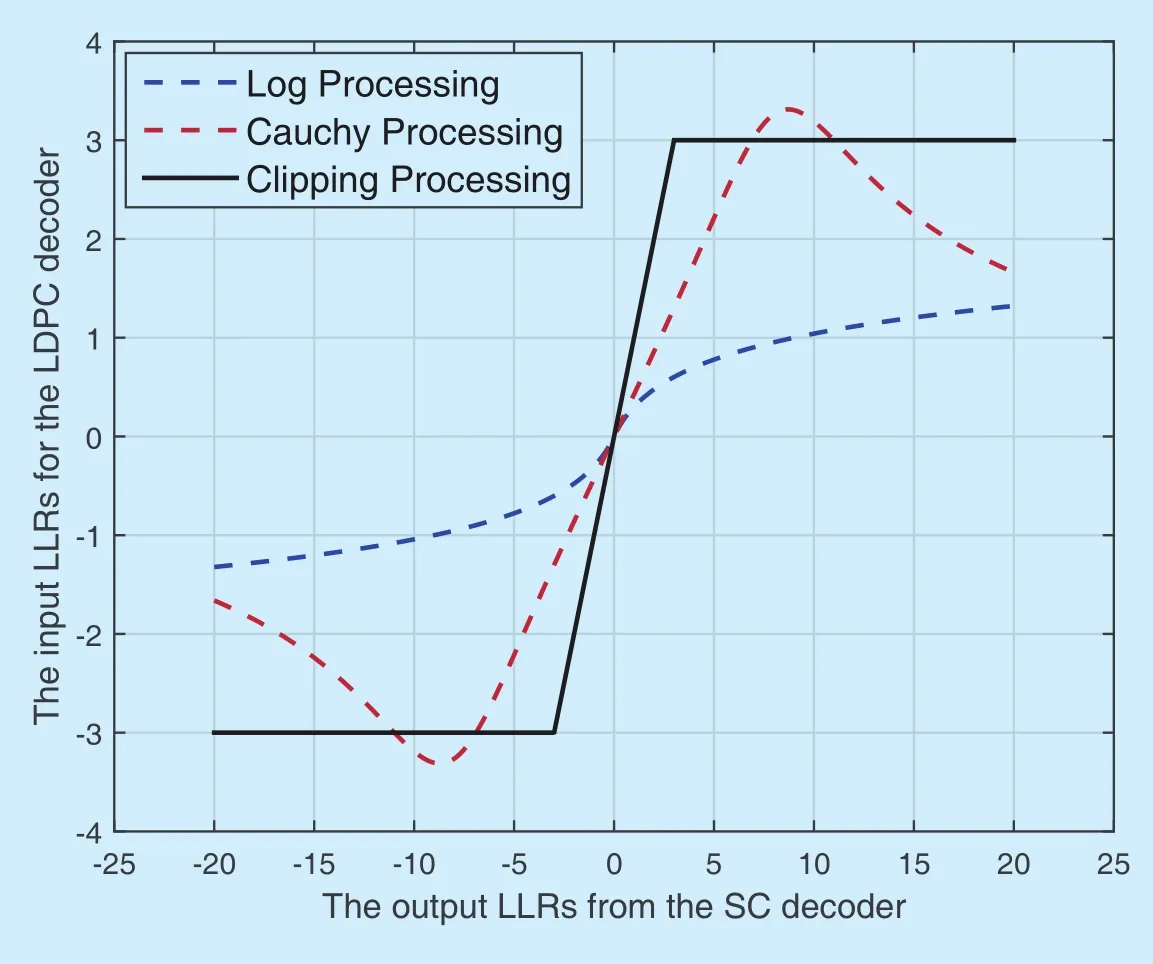
Fig.3.Input LLRs of the LDPC decoder as function of the output LLRs from the SC decoder.The block length of the polar code is N=256,and the code rate is R=1/4.The simulated SNR is Eb/ N0=6 dB.

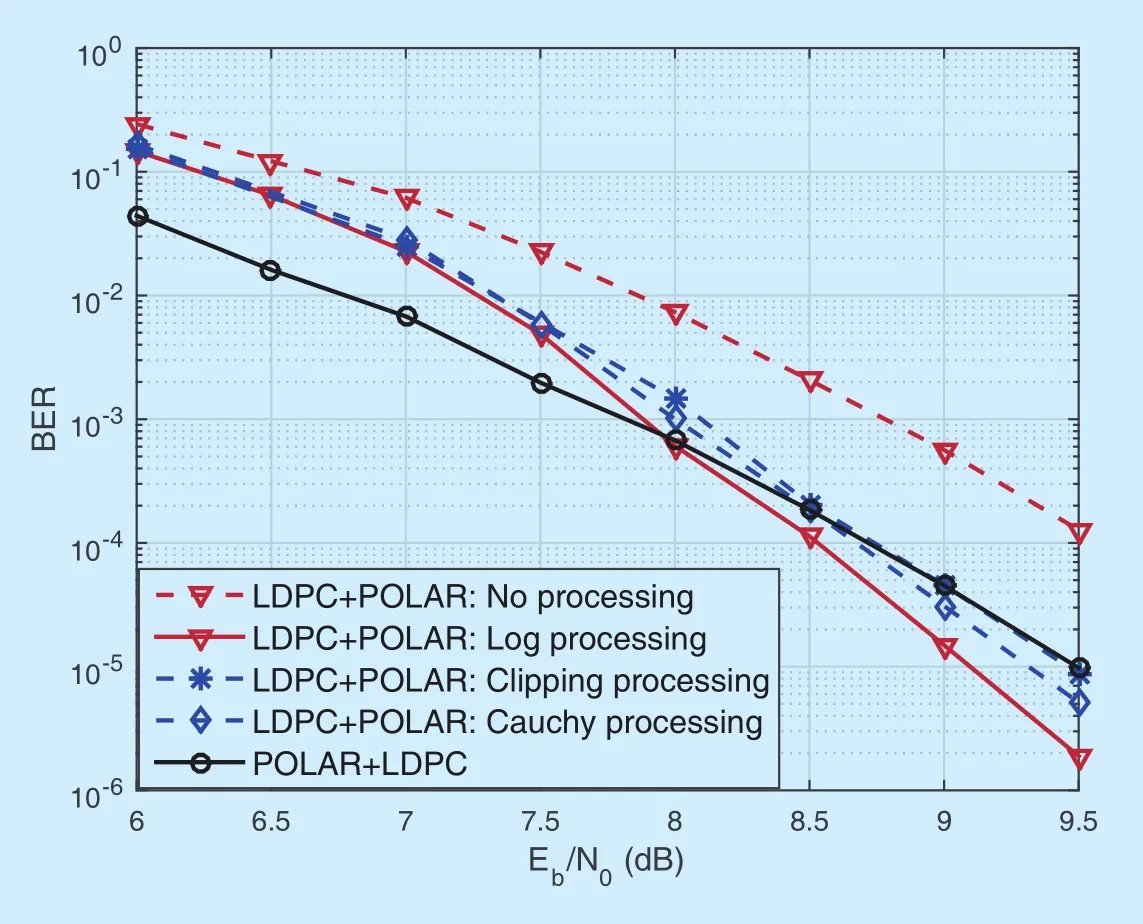
Fig.4.The BER performance of polar code (256,64) concatenated with a LDPC code in AWGN channels.The LDPC code is the (256,64) MacKay code.

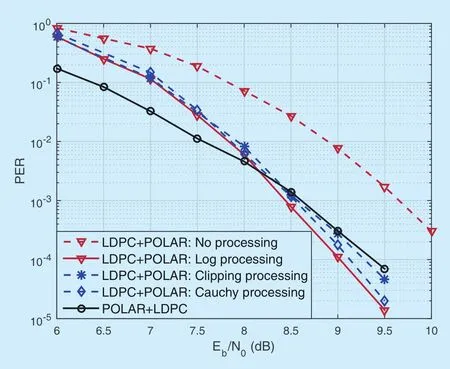
Fig.5.The BLER performance of polar code (256,64) concatenated with a LDPC code in AWGN channels.The LDPC code is the (256,64) MacKay code.

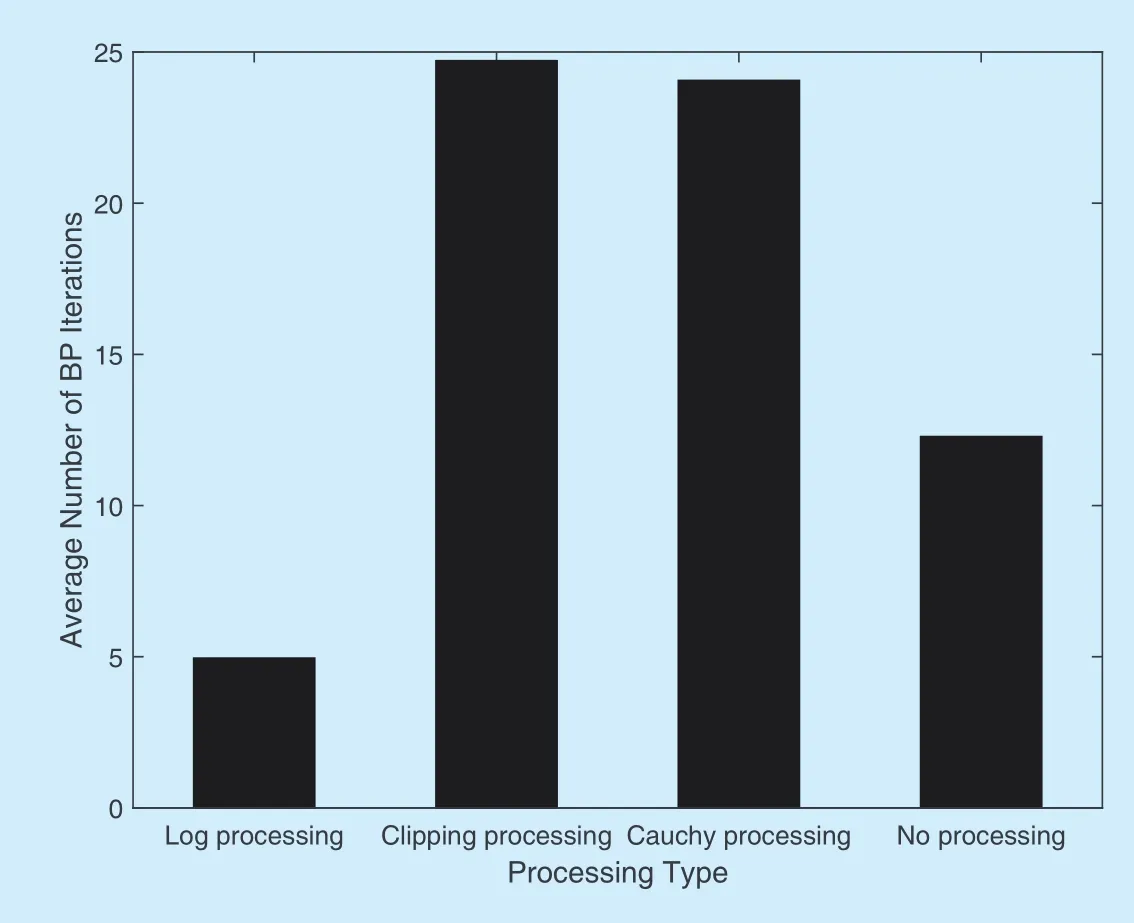
Fig.6.Average number of BP iterations required to decode each outer LDPC codeword at Eb/ N0=7 dB.

The BER performance of the concatenation scheme is shown in figure 4.At the simulatedEb/N0region,the POLAR+LDPC system outperforms the LDPC+POLAR system without the LLR processing,which shows the impact of the extreme incorrect LLR values from the SC decoding on the latter serial concatenation system.As observed,the concatenation system with the log LLR processing achieves a 1 dB gain compared with the counterpart without the log processing at a BER of 10-4.Also,at a BER =10-5,the LDPC+POLAR with the log LLR processing has 0.4 dB and 0.2 dB gains over the clipping scheme and the Cauchy scheme,respectively.

For any BLER smaller than 10-3shown in figure 5,the LDPC+POLAR concatenation system with the log LLR processing outperforms the POLAR+LDPC concatenation system.This proves that the log processing can weaken the impact of the extreme incorrect LLR values from the SC decoding on the decoding performance of the outer LDPC code.At a BLER =10-3,the LDPC+POLAR with the log LLR processing has a 1.2 dB gain compared with the system without the log processing.

The convergence speed of the outer LDPC code with the log processing,the clipping processing,the Cauchy processing,and without the LLR processing is also studied withEb/N0=7 dB.Speci fically,the average number of BP iterations for each correctly decoded codeword is evaluated and the result is shown in figure 6.It can be observed that the BP algorithm requires 4.95,24.71,24.06 and 12.28 iterations to successfully decode each LDPC codeword with the log LLR processing,the clipping LLR processing,the Cauchy LLR processing,and without the LLR processing scheme,respectively.This further shows the superior performance of the log processing scheme in the convergence speed.

V.CONCLUSION

In this paper,the LLR distribution from the SC decoding is studied to show the impact of the large absolute values of LLRs on the concatenation systems.To improve the performance of the LDPC+POLAR concatenation system,a log LLR processing scheme is developed.The LLR-distribution analyses and error-rate simulations illustrate that the LDPC+POLAR concatenation with the log LLR processing achieves better performance than the counterparts with clipping and Cauchy processing.Additionally,the proposed log LLR processing scheme significantly accelerates the convergence of the LDPC decoder.

ACKNOWLEDGEMENT

This work was supported in part by National Natural Science Foundation of China through grant 61501002,in part by Natural Science Project of Ministry of Education of Anhui through grant KJ2015A102,in part by Talents Recruitment Program of Anhui University,in part by the Key Laboratory Project of the Key Laboratory of Intelligent Computing and Signal Processing of the Ministry of Education of China,Anhui University.