Li Wang ,Xingmei Li ?,Lu Zhao ,Zailing Liu

1Beijing Key Laboratory of New Energy and Low-Carbon Development (North China Electric Power University),Beijing,People’s Republic of China

2Beijing Metallurgical Equipment Research Design Institute Co.Ltd,Shenggu Zhuang 2,Chaoyang,Beijing,People’s Republic of China

?E-mail:Xingmeil@163.com

Abstract:This research develops two new models for project portfolio selection,in which the candidate projects are composed of multiple repetitive units.To reflect some real situations,the learning effect is considered in the project portfolio selection problem for the first time.The mathematical representations of the relationship between learning experience and investment cost are provided.One numerical example under different scenarios is demonstrated and the impact of considering learning effect is then discussed.

1 Introduction

In today’s competitive market and resource shortage environment,companies attach great importance to how to effectively use scarce resources.The problem of how to select a subset of candidate projects to meet objectives without violating resources constraints is termed as project portfolio selection problem (PPSP).How to choose the project group,which maximises companies’ profit,is the main research content of PPSP [1].Besides,for different considerations and demands,some real-life factors,such as project scheduling,resource allocation,reinvestment,and project risks are considered to select the most profitable project portfolio.It is worth pointing out that Li et al.(2014) [2]introduced the concept of ‘project interruption (divisibility)’ into the project portfolio selection,where each candidate project can be partitioned into several sub-sections in different time periods.They assumed that the execution time of every sub-section of the project is the same.However,this assumption does not apply to the repetitive units projects (projects are composed of multiple repetitive units).

Repetitive units projects require construction workers to repeat their work in the same project.Hence,workers gradually accumulate learning experience.The number of direct labour hours that takes to finish an individual unit decrease as units increase.It is well known that the learning effect illustrates this phenomenon[3].Therefore,it is essential to introduce the learning effect into PPSP.Learning effect was first discovered in the aircraft industry 80 years ago,it has caused a stir because it is more applicable to reality.In 1936,Wright summed up the golden rule of learning effect,that is,whenever the aircraft output doubles,its production cost is reduced at a fixed rate [4].A large number of researches have subsequently emerged in this field.Several learning curve models have been developed,in which power,exponential and hyperbolic function models are the most respected [5].The power function learning curve model is derived from the summary of observations in the real company environment,which is the most practical and simple [6,7],so the power function learning curve model is considered to describe the learning effect in this paper.

How to choose repetitive units projects with consideration of interruption is our concern,and interruptions can have detrimental impacts on project execution,particularly the loss of learning effect [8].Common sense is that the length of the interruption period is the primary factor in the deterioration of performance [9].Hancock indicated that very short breaks,such as coffee times,had no effect on learning,whereas overnight and longer breaks definitely retarded the learning process [10].We are mainly concerned with these two situations in repetitive units PPSP.Moreover,in order to reflect the reality,cardinality restrictions,reinvestment,set-up cost and interruption (divisibility) were incorporated into the model proposed in this paper.

The main contributions of this paper include the following three points.Firstly,the paper introduces the learning effect into project portfolio selection,which bridges the gap between PPSP and learning effect.Secondly,this paper further develops the learning effect model.Then,expanded new models of the project portfolio selection with learning effect are constructed.Thirdly,considering the learning slope in different project backgrounds is different,this paper analyses the sensitivity of learning slope and discusses the impact of different learning effects on project investment cost and benefit.

The remaining part of this paper is organised as follows.In Section 2,we first provide the notations and problem statement in this paper.Then the learning curve effect is introduced,followed by the calculation of investment cost.In Section 3,we formulate the expanded model and special model for the PPSP with learning effect.Numerical examples under three scenarios are provided in Section 4 to highlight the characteristics of the proposed models.In Section 5,we conclude this paper and show the directions of future researches.

2 Model formulations

In this section,for discussion convenience,we will first provide the notations used in this paper and describe the problem.The learning curve will then be introduced.On this basis,the investment cost considering the learning effect will be given.A special situation with the total forgetting of the learning effect will also be shown.The two situations will clearly reflect the impact of the learning effect on project investment cost.

2.1 Notations

V set of candidate projects,indexed by jV,j=1,2,...,n L set of time periods in the planning horizon,indexed by t=1,2,...,T.Period t starts at time point t ?1 and ends at time point t

K (t)financial resources directly available from external sources at a specific time point t.Especially,K (0) represents financial resources that are available initially

N maximum number of selected projects over the entire planning horizon

Mtmaximum number of executed projects in each time period t for tL

cjset-up cost when a portion of the project j is executed in a time period,jv

bjreturn of the whole project j when it is completed,jv

zjbinary variable,taking value 1 only if the project j is selected from v

yjtbinary variable,taking value 1 only if the proportion of project j is executed in the time period t,where jv and tL r basic interest rate or the market cost of the capital

ajtminimum threshold for the portion of the project j to be executed in the time period t

bjtmaximum limitation for the portion of the project j to be executed in the time period t

xjtdecision variables in the interval[ajt,bjt],denoting a proportion of project j executed in the time period t

Ajproportion of project j– the smallest repeatable unit of the project j

njtotal number of repeatable units included in the project j,njAj=1 mjtnumber of repeatable units executed of the project j during the time period t

ujtnumber of repeatable units executed of the project j before the time point t

Tmjttotal production time for executing mjtrepeatable units of the project j during the time period t

vjtime cost conversion factor

2.2 Problem statement

Considering,a resource-constrained PPSP in a project-oriented company.This company needs to select an optimal project portfolio from V candidate projects,among them are composed of multiple repetitive units,which can use the learning curve to characterise projects’ execution time.A common sense is that interruption can have detrimental impacts on project execution.In order to reflect this reality,two different interruptions,which will be introduced in Sections 2.3 and 2.4,respectively,are taken into account in this paper.The company’s goal is to maximise the net present value (NPV) of the project portfolio.For the convenience of building the model,some assumptions are given as follows:

? Each candidate project is composed of njrepetitive units.

? Investment cost is only related to the execution time of one project,interruption time is not included in the execution time.

2.3 Learning curve

Fig.1 can help us better understand the learning effect.As shown in Fig.1,the horizontal axis means the number of repetitive units of one project.The vertical axis is the time required to produce a repetitive unit.The time required to produce the (x+1)th unit is assumed to always be less than the time for the xth unit.The reduction in time is a monotonically decreasing function,as described in Wright’s paper [11].

Wright’s learning curve model is shown as follows:

where Txis the time to produce the xth unit,a0is the theoretical time required to produce the first unit,x is the production unit and s is the learning slope s=?log(LR)/log(2),s[0,1).

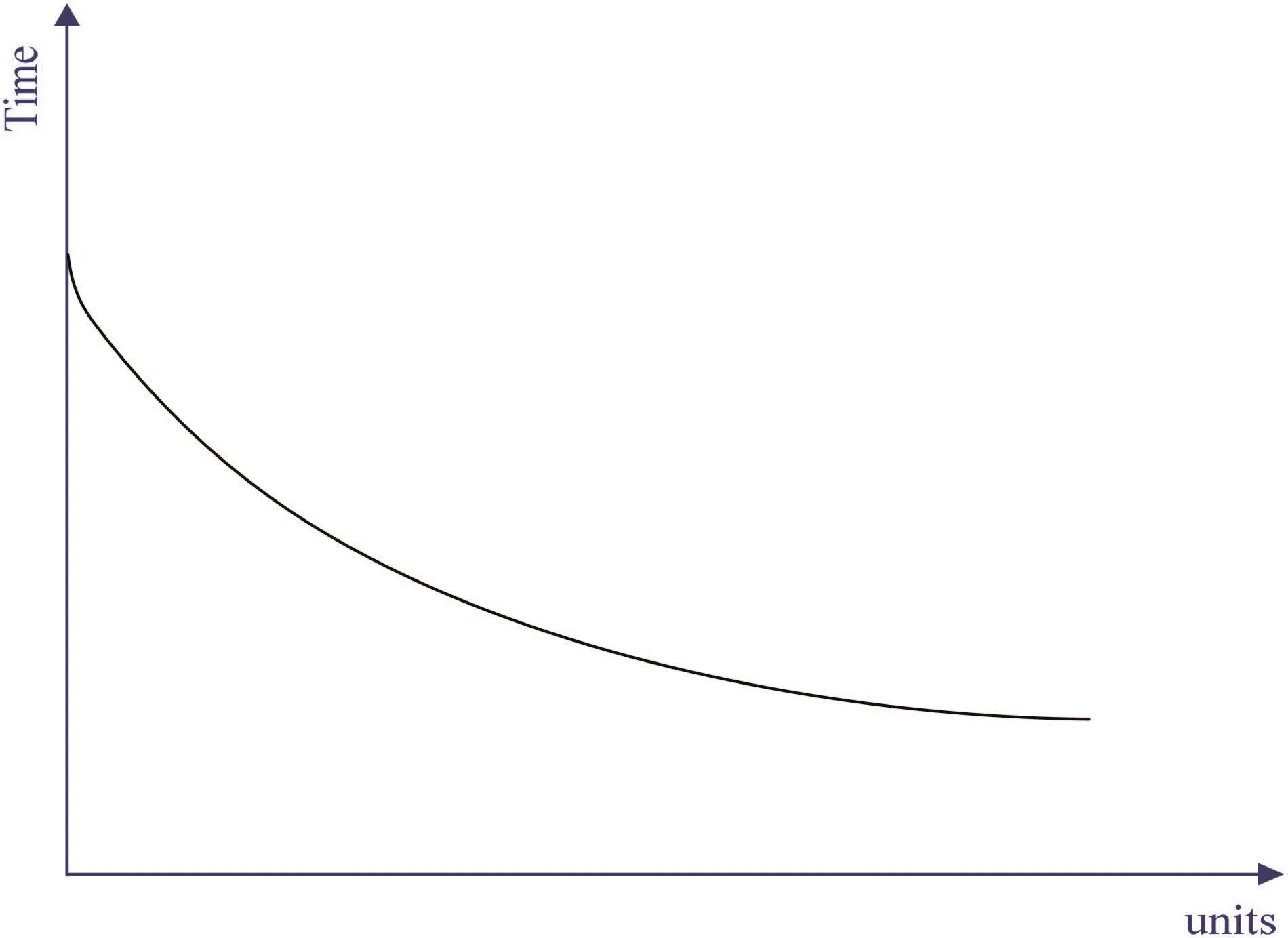
Fig.1 Learning curve

a0is always assumed to be known when one project is first executed.We also assume that the execution units of project j are mjtin thetth time period.According to Fig.1,if we use interval method over [0,mjt],the time required to complete mjtrepetitive units is easy to be obtained.Then,Tmjtcan be calculated.

2.4 Investment cost considering learning effect

The learning effect affects the project’s investment cost by affecting the completion time of the project.Based on this consideration,we need to firstly get the project actual completion time.

In this section,we will discuss the first situation-the interruption is short.When the interruption is over and the project j is re-executed,there will be no effect on the learning experience.As shown in Fig.2.

Note that the project j short interruption happens,there is no loss of learning experience.Based on this consideration,the calculation formula of Tmjtfor t ≥2 is

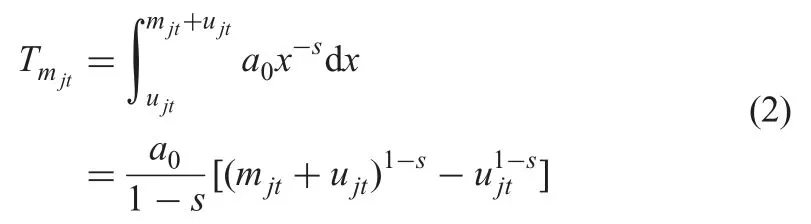
The investment cost is provided as follows:

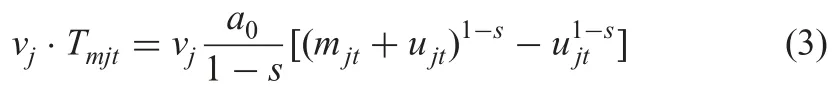
2.5 Investment cost under special situation

When the project j is interrupted,there will also exist a situation whereas longer breaks definitely retard the learning process.In this section,we will consider a special situation,where the interruption is too long to re-accumulate the learning experience,as shown in Fig.3.

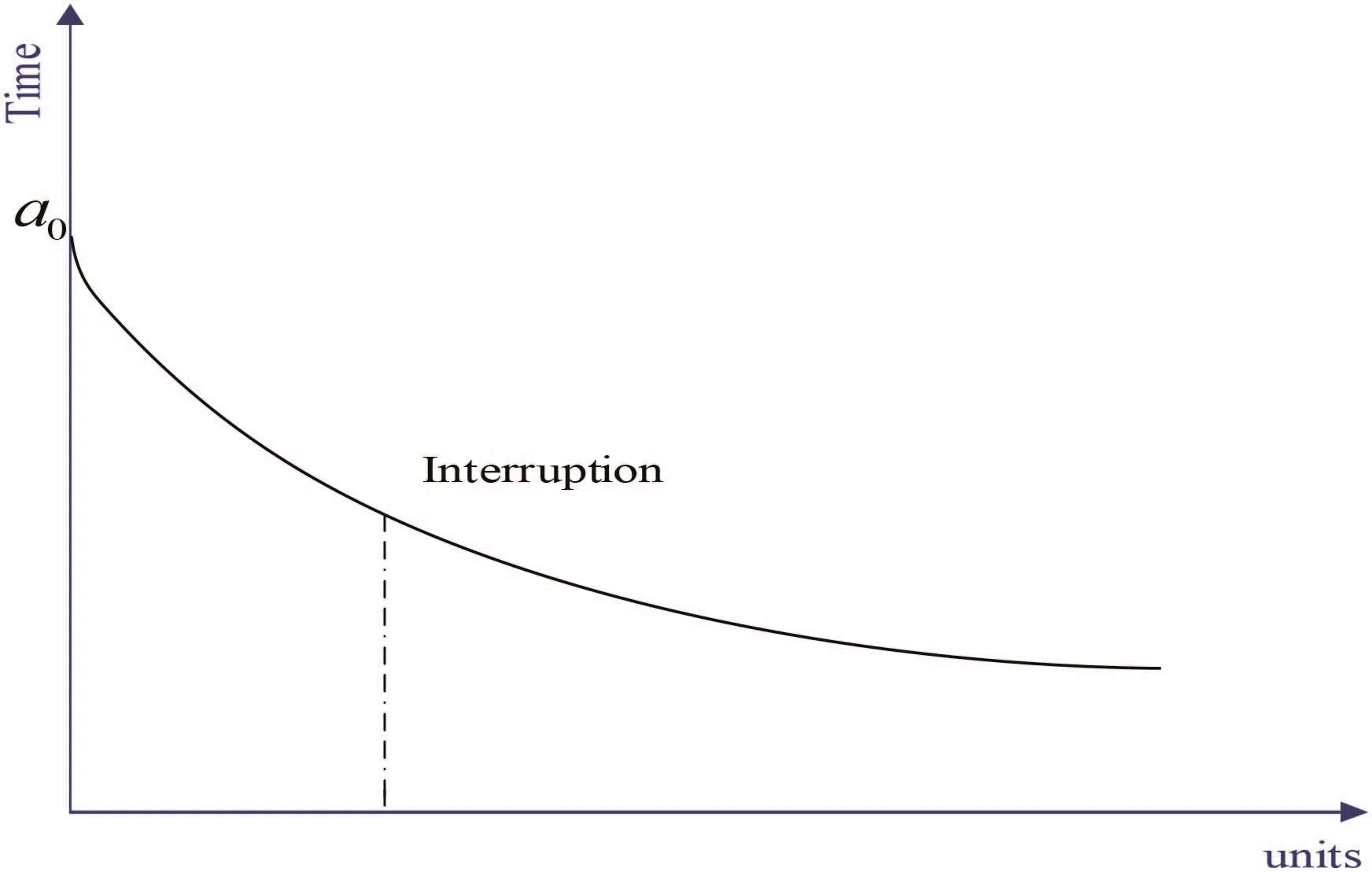
Fig.2 Learning effect curve with short interruption

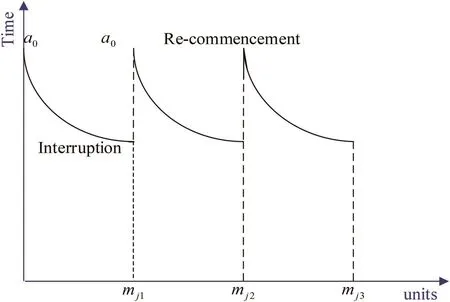
Fig.3 Learning effect curve under special situation

When the accumulation of learning experience is not considered,as long as the execution of the project j is interrupted,the time required to produce the first unit is still a0when the project is re-executed next time.In other words,the learning curve function is still Tx=a0x?safter an interruption.So the calculation formula of Tmjtis

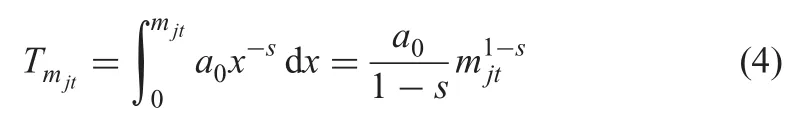
The investment cost under special situation is considered as follows:

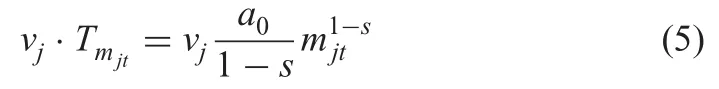
3 Expanded models of the PPSP with learning effect

In this section,we will discuss the project portfolio selection models with learning effect in different scenarios.The PPSP is to maximise NPV without violating financial constraint and resource constraints.

3.1 Expanded model with learning effect

In the first scenario,we will discuss project portfolio selection model considering learning effect.We think there will be no effect on learning effect when the interruption is over and the project j is re-executed.Therefore,the objective function is to maximise the NPV,which is shown as follows:

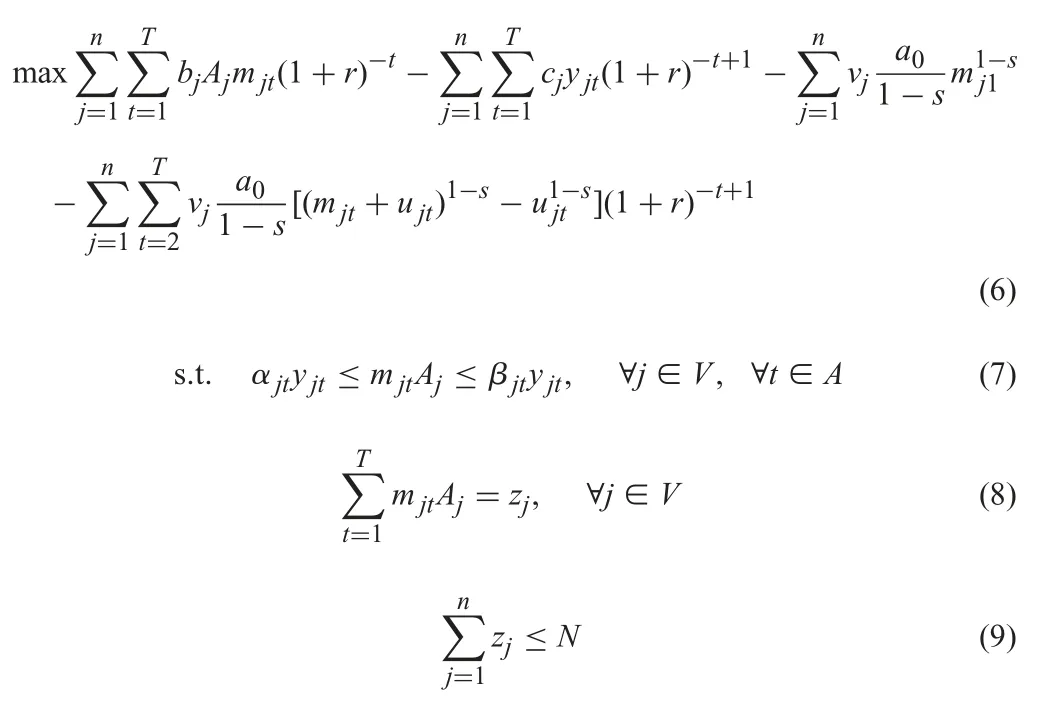
The objective function (6) represents the NPV of the executed projects when the learning effect is considered.Constraint (7)shows that for each selected project,either it is not executed during the time period t (mjt=0,yjt=0),or the executed portion must exceed the minimum threshold and not exceed the maximum limitation in the time period t (ajt≤mjtAj≤bjt,yjt=1).Constraint (8) indicates that any selected project must be completed over the entire planning horizon.Constraints (9)and (10) are introduced to control the total numbers of executed projects over the whole planning horizon and in each time period,respectively.Constraint (11) shows the relationship between the number of repetitive units in the project j and the proportion of each repetitive unit;Constraint (12) indicates that the variables yjtand zjare Boolean variables.Constraints (13) and (14) show that the financial resources at each time point must be enough for the set-up cost and investment in the next time period.Also the initial financial resource k (0) must ensure that it is available for the execution of the projects in the first time period.

In this scenario,we think the interruptions have no effect on learning,so Tnj(the total execution time of project j) is not changed.According to the definite integral property,it is obvious that (15) is established,see Figs.4 and 5.

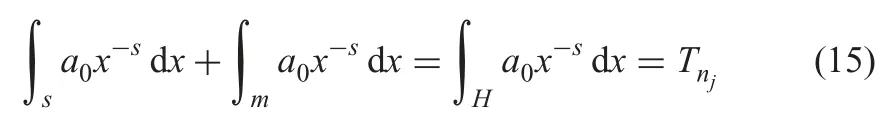
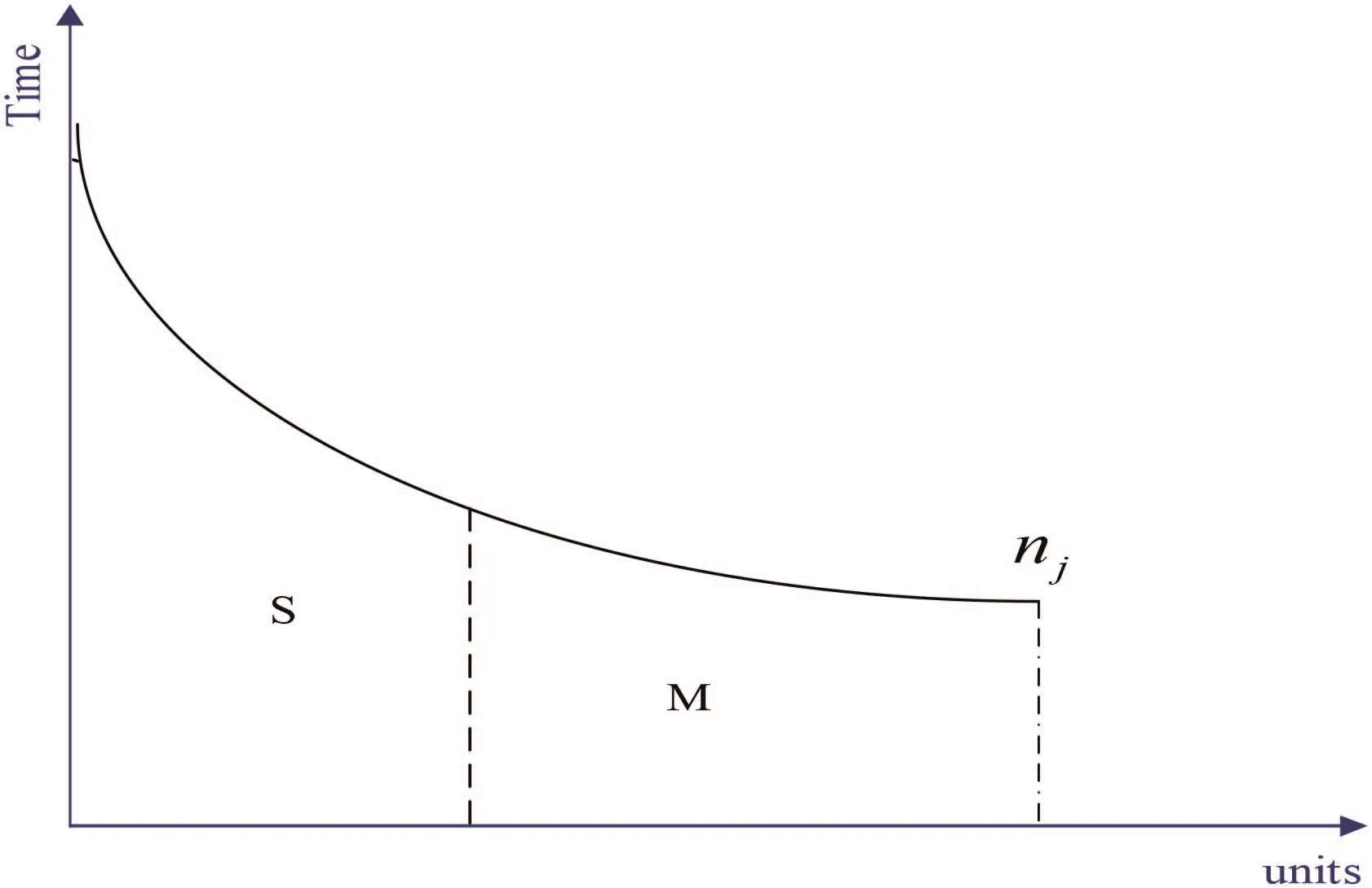
Fig.4 Special learning curve

Fig.5 Traditional learning curve

Since Tnjis the same,the investment cost is the same,(16) is established

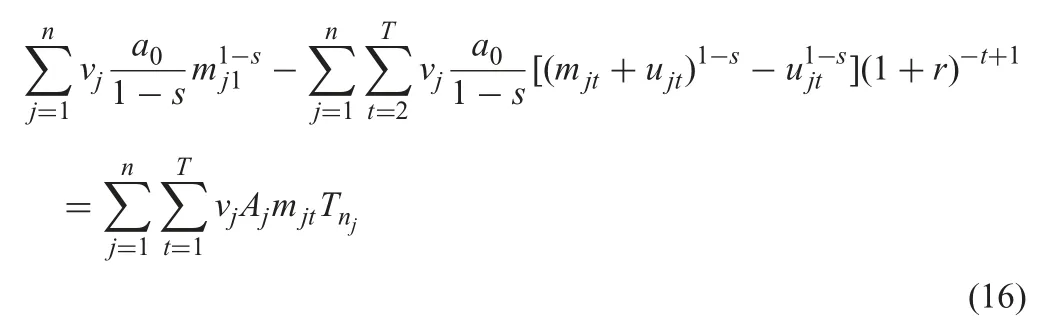
In order to get the result more easily,we give(6)the equivalent(17)as follows:

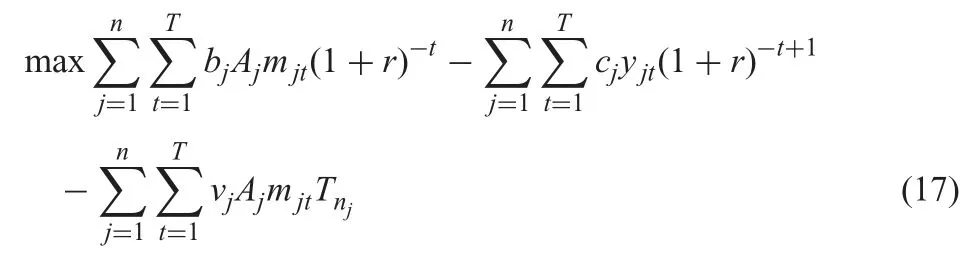
However,we think each unit has the same production time a0in the traditional PPSP model.Therefore,the traditional model’s objective function is to maximise the NPV,which is shown as follows:

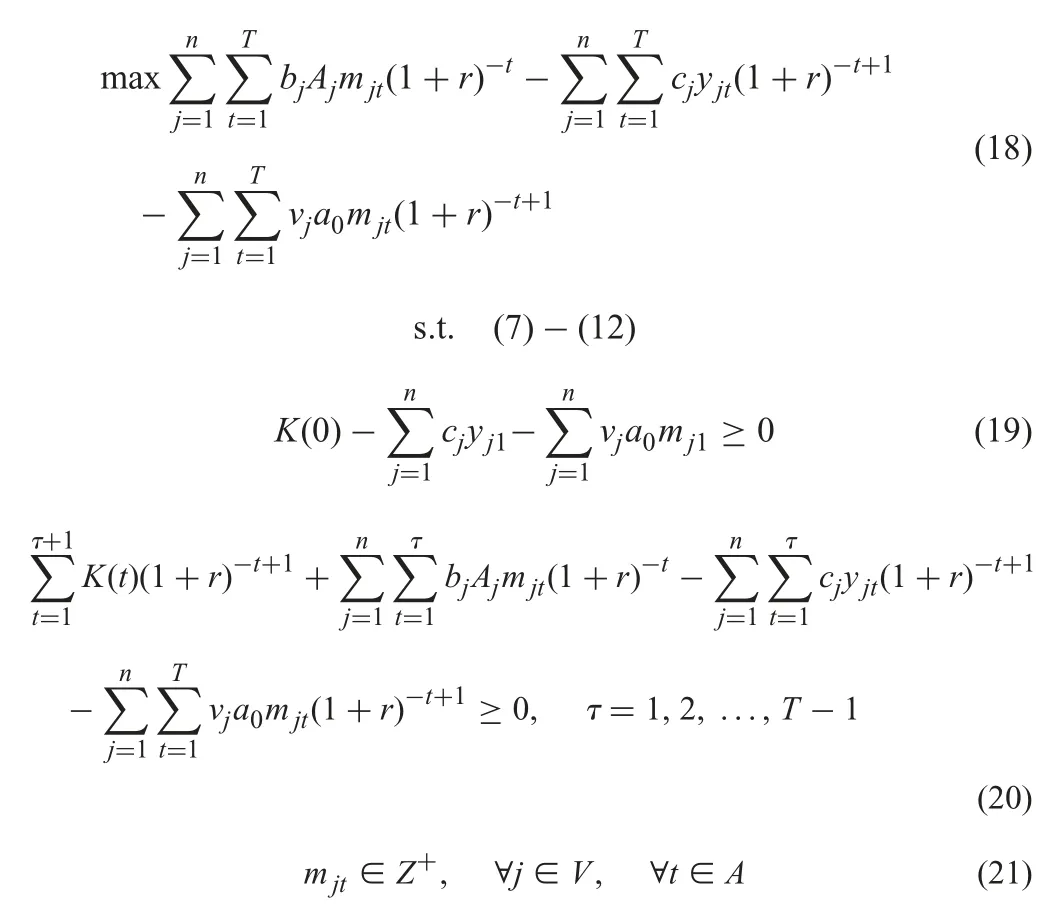
The objective function (18) represents the NPV of the executed projects.Constraints (19) and (20) require that the financial resources at each time point must be enough for the set-up cost and investment in the next time period.Also the initial financial resource k (0) must ensure that it is available for the execution of the projects in the first time period.Constraint (21) indicates mjtare integer variables.

3.2 Special model with learning effect

In this section,we will consider a special situation,where the time of interruption is so long that need to re-accumulate the learning experience.Therefore,the objective function is to maximise the NPV,which is shown as follows:

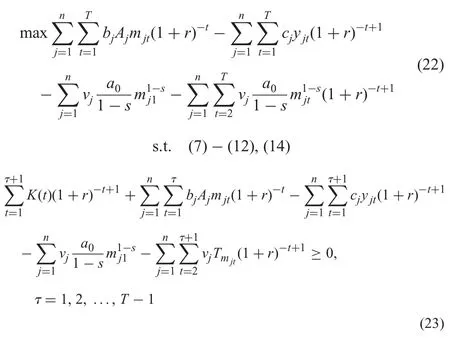
The objective function (22) represents the NPV of the executed projects when learning is almost retarded.Constraint (23) shows that the financial resources at each time point must be enough for the set-up cost and investment in the next time period.

Numerical examples are provided and processed to highlight the capability and characteristics of our proposed model in Section 4.

4 Numerical example

Since the project selection problem belongs to the NP-hard problem,the difficulty of the problem is further increased after the learning effect is introduced.In this paper,the GAMS is used to analyse the data to find the maximum value of the objective function,so as to highlight the capability and characteristics of the project portfolio selection model considering the learning effect.

Here,we take an example to illustrate the impact of considering learning effect in PPSP.In this case,assume that the set of candidate projects for the planning horizon is 10 (V=10),the planning horizon is divided into five time periods (T=5).The investment required for each project,the return of the project when it is completed,and the initial funds at each point are shown in Tables 1 and 2.

Additionally,the set-up cost for each candidate project is$1 million (sj=1,for jv).The production time required to produce the first unit is 1 (a0=1),the maximum number of selected projects over the entire planning horizon is 7 (N=7),and the maximum number of executed projects in each time period t is 3 (Mt=3).Specially,for the interruption model,the lower and upper bounds for each project are 0.2 and 0.5 (ajt=0.2,bjt=0.5),respectively.Moreover,assume that r=5%.

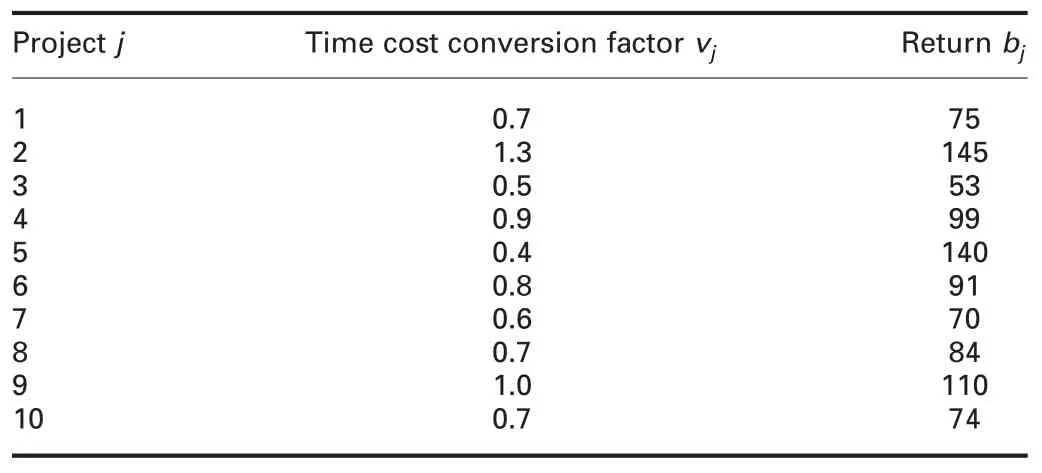
Table 1 Return bjand the time cost conversion factor of each project j(1 million dollars)

Table 2 Financial resource K(t) at each time period (1 million dollars)

By solving the model,the optimal portfolio and schedule are shown in Table 3.We first explain the symbols in Table 3.For example,2 (0.50) means that 0.5 portion of project 2 is executed in time period 1.Other data can be explained in a similar way.In Table 3,we can see that the number of selected projects in optimal solution is 7.All the selected projects are divided into two parts.The maximum NPV is $183.017 million if the learning effect is not considered.

Keep the above data unchanged,consider the learning effect and further verify the impact of the learning effect on the PPSP.In order to highlight the significant influence of learning effect,this paper selects the classical observation learning rates [11],which are 90,80,70%,respectively,and the corresponding learning slopes are 0.152,0.332,0.515,respectively.Then we get the portfolio selection and the objective function values under the three learning slopes,as shown in Table 4.The value of the objective function changed from $183.017 million to $397.670 million,$540.805 million,and $610.208 million.This result indicates that the benefit is higher when we consider learning effect.Meanwhile,the higher the learning slope is,the higher the return is.

The learning effect is introduced into the special model but learning experience is fully forgotten when an interruption occurs,and these three classic learning rates are still adopted.At this point we get the portfolio selection and the objective function values under the three learning slopes,as shown in Table 5.The objective function values under three learning slopes are in the order of $284.1815 million,$414.5633 million,and $479.8998 million,respectively.The total number of projects executed during the entire planning horizon is 6.When s=0.152,projects 2,4,5,7,8 and 9 are executed.When s=0.332 and s=0.515,the executed projects become 2,4,5,6,8 and 9.In addition,it is worth noting that when s=0.152,project 5 is executed during the first,second,and third periods,and the portion is executed at 24,34,and 42%,respectively.

Table 3 Optimal portfolio,schedule and proportions of the projects for model without considering learning effect

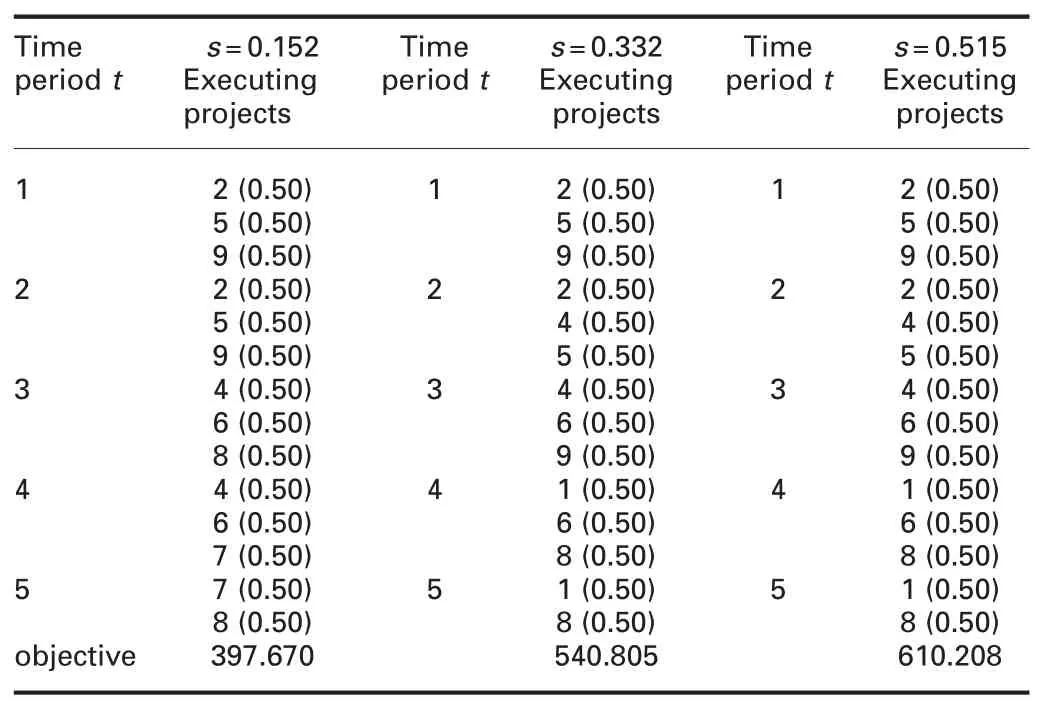
Table 4 Optimal portfolio,schedule and proportions of the projects for the expanded model

A comprehensive comparison of considering the learning effect,looking at Figs.6 and 7 can draw the conclusions:(i) With theconsideration of learning effect,the objective function value is higher than without it;(ii) Considering the learning effect,the higher the learning slope is,the higher the return is;(iii) Under the condition of the same learning slope,the benefit in expanded model is higher than in the special model;(iv) Different scenarios will affect project portfolio selection,the proportion of project execution and the execution time period.

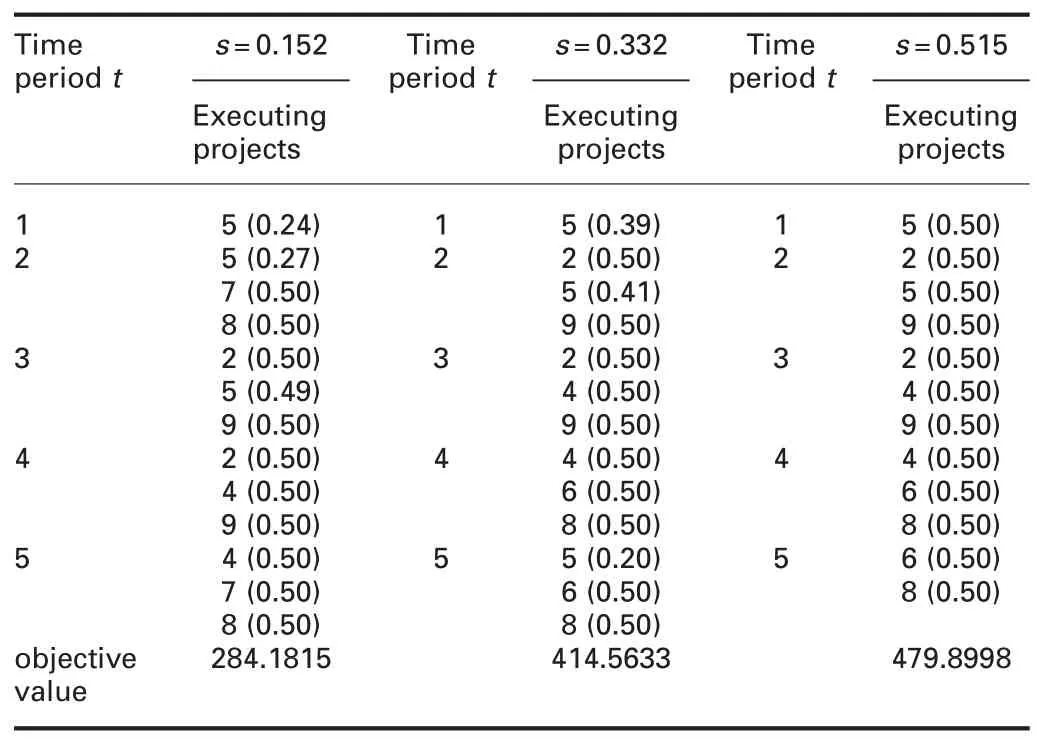
Table 5 Optimal portfolio,schedule and proportions of the projects for the special model

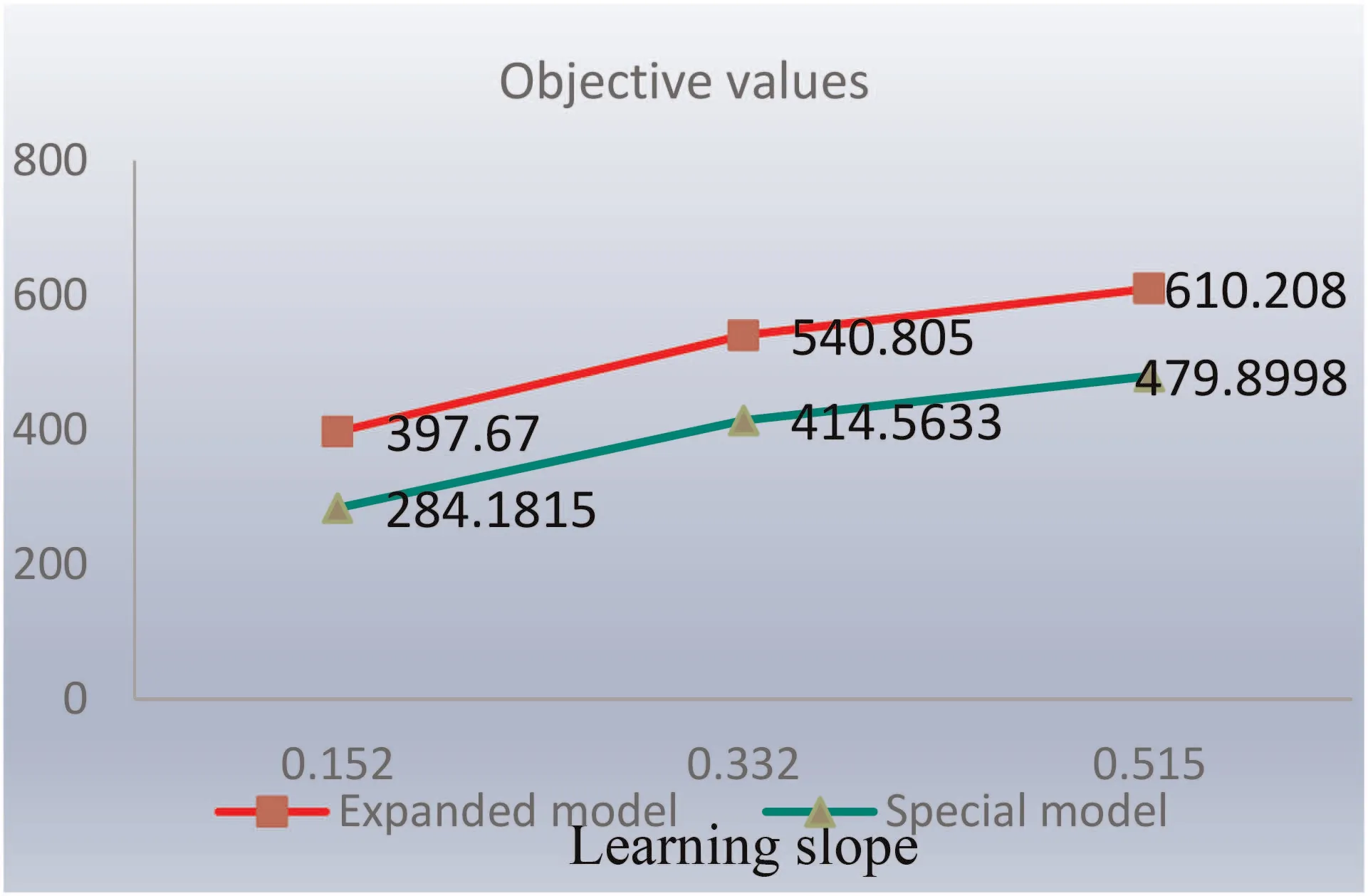
Fig.6 Difference between the expanded model and the special model

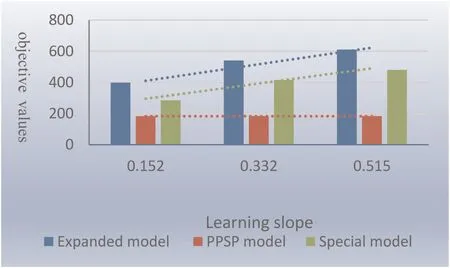
Fig.7 Comparison between three different models

The numerical examples prove that the introduction of the learning effect has certain influence on the benefit,the executed project,the execution portion and the execution phase,which also provides a reasonable explanation for the deviation of the income budget of the company.In order to make the company income budget more accurate,the learning effect must be considered when a project portfolio is selected.

5 Conclusion

This paper examines the project portfolio selection,in which the candidate projects are composed of multiple repetitive units.Meanwhile,the learning effect is introduced into the project portfolio selection models for the first time.Then,an expanded project portfolio selection model considering learning effect is provided.Two different kinds of scenarios are discussed and we can draw a conclusion that the learning effect has certain influence on the benefit,the executed project,the execution portion and the execution phase.

However,we just discussed two situations in which the learning effect is considered and a special case.In the future,we will consider a more complicated situation where the learning effect is partially forgotten and partially inherited.In contrast,this situation is more applicable to the reality.

6 Acknowledgment

This work was supported by the National Natural Science Foundation of China (71772060).The authors thank the editors and anonymous reviewers for their thoughtful and valuable comments.