Totan Garai,Harish Garg ?

1Department of Mathematics,Silda Chandra Sekhar College,Jhargram-721515,West Bengal,India

2School of Mathematics,Thapar Institute of Engineering &Technology,Deemed University,Patiala-147004,Punjab,India

?E-mail:harishg58iitr@gmail.com

Abstract:This study presented a multi-objective linear fractional inventory (LFI) problem with generalised intuitionistic fuzzy numbers.In modelling,the authors have assumed the ambiances where generalised trapezoidal intuitionistic fuzzy numbers (GTIFNs) used to handle the uncertain information in the data.Then,the given multi-objective generalised intuitionistic fuzzy LFI model was transformed into its equivalent deterministic linear fractional programming problem by employing the possibility and necessity measures.Finally,the applicability of the model is demonstrated with a numerical example and the sensitivity analysis under several parameters is investigated to explore the study.

Nomenclature

n number of items in the inventory

k fixed cost per order in every cycle

F total available space of all item

B total available budget of all item

hiholding cost per unit item of ith item

Siselling price per unit item for ith item

Qiordering quantity per unit of ith item

Pipurchasing cost per unit of ith item

Didemand quantity per unit item of ith item

OCiordering cost per unit item of ith item

fithe space required per unit of ith item

1 Introduction

In 1965,Zadeh [1]proposed the fuzzy set (FS) theory which is an exhibited in a wide variety of real problems.He discloses the degree of membership of a certain element in the FS,but taken the other degrees as a complement to 1.However,in practical problem,this situation may not happen.For handling this type of problem,Atanassov [2]initiated the idea of intuitionistic FS (IFS)by incorporated a degree known as degree of non-membership along with membership degree such that their sum isn’t more than one.This representation will give more degree of freedom to the decision-makers to evaluate the given objects than FSs.The intuitionistic fuzzy number (IFN) is a generalisation of the fuzzy number,which is a special kind of IFS defined on the real number set [3].Garai et al.[4]proposed the generalised IFN (GIFN) more generally.

Due to the increase in the system complexity day-by-day,it is very common and difficult in the real world problem to handle the fuzziness in the data.For this type of problem,a theory of FS is a well-known technique.However,the concept of the Possibility theory [5]is also one of the methods to handle uncertain information.Thereafter,many researchers worked on this area(i.e.[6–8]).Then,Liu and Liu [9]introduced a credibility measure which is an average of possibility and necessity measure.Credibility measure is a self-dual measure.Dubois and Prade [6]formulated a fuzzy mean using credibility measures.Then,possiblistic mean and variance of fuzzy numbers were introduced by Carlsson and Fuller [10].Using the possibility theory Heilpern[11]defined the expected value of fuzzy variable (i.e.expected value operator).The application of expected value operator called expected value model which was proposed by Liu and Liu [9].Garg [12]presented the credibility measures to compute the reliability of the series–parallel systems with different types of the IFNs.Garai et al.[13],Garai et al.[14]solved an inventory problem using possibility mean under generalised intuitionistic fuzzy environment.

In multi-objective inventory problems under uncertain environment,the decision-makers are often required to optimise two or more objectives at one time.First time,Roy and Maiti [15]presented a multi-objective inventory model in fuzzy environments and it’s solved by geometric programming approaches.Garg et al.[16]presented a multi-objective optimisation model for reliability problem by using IFNs.Rani et al.[17]presented a model for solving the non-linear optimisation model based on IFNs.Jafariana et al.[18]proposed a flexible programming approach for solving multi-objective non-linear programming problems in intuitionistic fuzzy environment.Recently,Garai et al.[19]considered the chance-operator techniques to solve the multi-item inventory models.Dutta et al.[20]solved multi-objective linear fractional (MOLF) programming problem using a set theoretic approach.Thereafter,Dutta et al.[21]proposed a linear fractional multiple criteria optimisation problem considering the fuzzy approaches.A possibility programming approach for stochastic fuzzy multi-objective linear fractional is considered by Iskandar[22].Sadjadi et al.[23]developed a MOLF inventory model by fuzzy approach.Dutta and Kumar [24]proposed a MOLF inventory model with fuzzy goal programming approach.Garg[25]presented the fuzzy inventory model for deteriorating items under the different types of lead-time distribution.Ali et al.[26]formulated a fractional inventory management problem in intuitionistic fuzzy environment.

In the inventory modelling,the parameter associated with them is usually non-crisp which also depict the behaviour of the systems.For example,in it,the holding cost is always depending on the storage quantity.Also,the replenishment cost is entirely depending upon the whole amount of product to be produced in a length of the cycle.So,the maximum total profit of the practical inventory problem is uncertain nature.In these conditions,IFS may be applied for the formulation of inventory problems.To the best of author’s knowledge,no attempt has been done by considering the different features of the inventory model as GIFNs.Thus,the aim of this study is to solve the multi-objective linear fractional inventory (LFI) model by developing a model with GIFNs and the concept of possibility and necessity measures.

The rest of the organisation of the work is given as follows:In Section 2,some basic concepts related to GIFNs,possibility and necessity measures are presented.In Section 3,we introduce the notations and assumption which are used throughout the paper and formulated multi-objective generalised intuitionistic fuzzy LFI model.In Section 4,we developed a novel method to solve the model.The applicability of the approach is demonstrated in Section 5.Finally,the conclusion is drawn in Section 6.

2 Preliminaries

Definition 1:A generalised IFN over the real number R,is defined as [4]

Definition 3:(possibility and necessity of GIFNs):be two GIFN with membership functionsand non-membership functionsrespectively,and R be the set of the real number.Then the possibility and necessity ofandare given by [4]

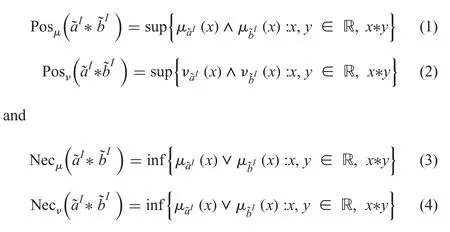
Where Posm,Posnare the notations for the possibility of membership and non-membership functions,Necm,Necnare the notations for the necessity of membership and non-membership functions of GIFNs,and ‘*’ represent any relations of

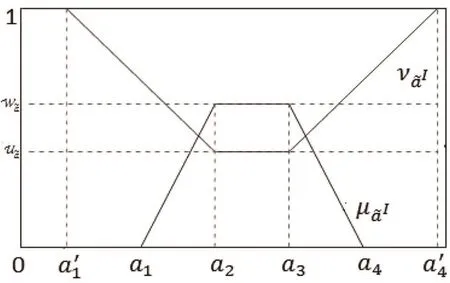
Fig.1 Membership and non-membership functions of GTIFN ()

Definition 4:(Measure of a GIFN):Letbe a GIFN.Then the measure [4]offor membership functions are defined as follows

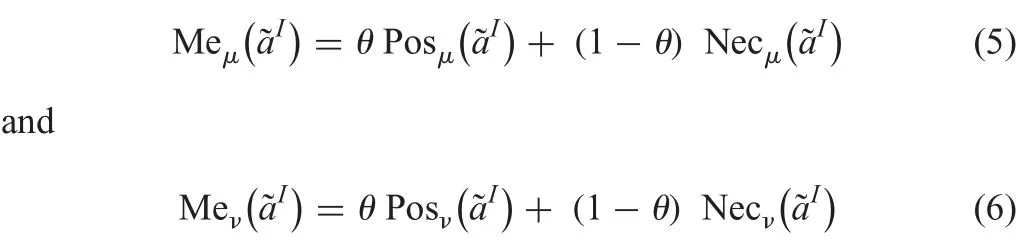
For the optimistic and pessimistic parameterwe define as follows

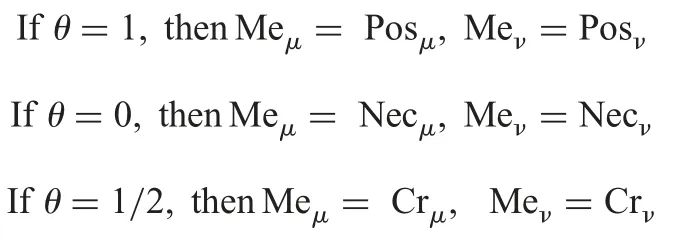
Where the notation Cr represents the credibility measure and defined as follows

Fig.2 Membership function of GTIFN ,,and Posm( ≤)

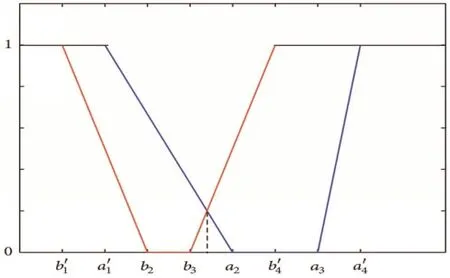
Fig.3 Non-membership function of GTIFN ,,and Posn

Similarly,we also calculate necessity measures

3 Multi-objective generalised intuitionistic fuzzy LFI model

Generally,in linear programming inventory problem,we have optimised the profit function,inventory cost,additional cost etc.under certain subject constraints.This linear inventory problem can represent as single-ratio LFI problem (Ali et al.[26])considering by numerators (input,profit,cost,capital,risk,or time) and denominators (input,profit,cost,capital,risk,or time).In this way,we have solved the sum-of-ratios problem of applications of the multitude.We have considered this type of technique when the optimum result of some inventory problem can not get good results in the general way.Therefore,here we have proposed the multi-objective inventory problem presented in this technique.The following assumptions and notations which have used in the formulation of the proposed LFI problem.

3.1 Assumptions:

(i) Lead time is zero.

(ii) In the inventory model,we considered multi-objective.

(iii) There is only one period and time horizon is infinite.

(iv) For each item,demand rate is constant over time period.

(v) Holding cost is constant and known for each item

(vi) Purchasing cost for each item is constant.

(vii) Shortages are not allowed.

(viii) Deterioration not allowed.

Here,we have presented a multi-objective model with resources constraints as linear fraction programme problem.This multi-objective inventory problem formulated by two constraints one is investment and the other is limited capacity of the warehouse.For each item demand of this inventory is constant and known.The time horizon of the inventory is infinite and lead time is zero.We consider replenishments are instantaneous and without shortages.In real life,we look at multi-objective inventory problem very useful than the single objective inventory problem.Now,we solve a ‘multi-objective inventory model with fractional objective functions’.

Hence the MOLF inventory model with budgetary,space,and investment constraints is given by

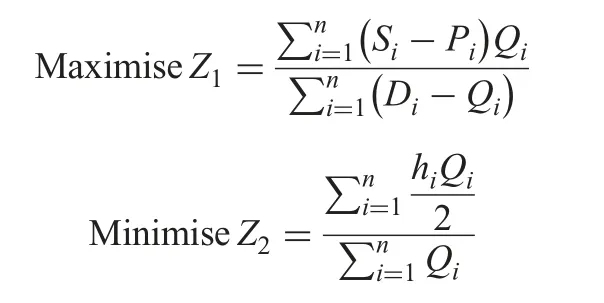
Subject to the constraint

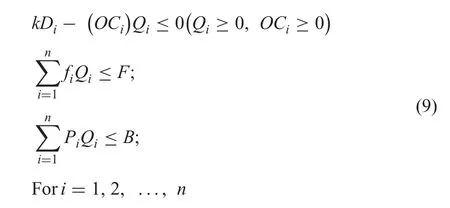
Here,Constraint I indicates the ‘budgetary constraint on ordering cost’.For the nth item ordering cost can be written as follows:

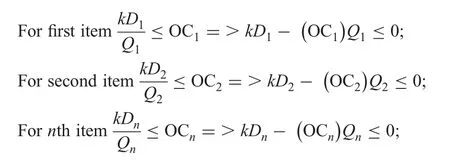
Constraint II indicates ‘restriction on the warehouse areas’.

Constraint III indicates ‘the upper limit of the total investment’.

In the inventory systems,different costs are imprecise natures.For example (i) the holding cost of the inventory may not be fixed in previously,and it may change over time length.(ii) Due to the behaviours of customers’ requirements of the demand for items cannot be fixed in advanc,it is always changeable.Similarly,the ordering cost,selling cost,and purchasing cost of an item cannot be prefixed.So,all these cost parameters of the inventory problem that are selling cost,purchasing cost,ordering cost,holding cost,and demand are may be uncertain or vague.This vagueness or uncertainty may be capture in intuitionistic fuzzy environment.For truckle these situations,generalised intuitionistic fuzzy environment can be considered as the formulation of inventory problems.Therefore,all parameters including selling cost,purchasing cost,ordering cost,holding cost,and demand of the inventory are considered as GIFNs.After all these above amendments,the model (9) can be formulated as follows:

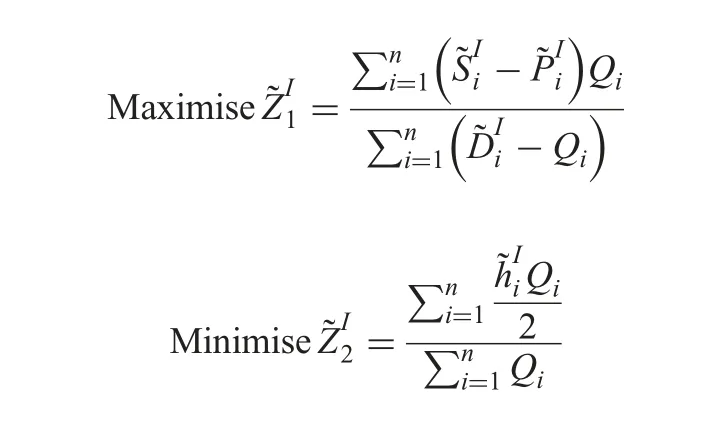
Subject to the constraint

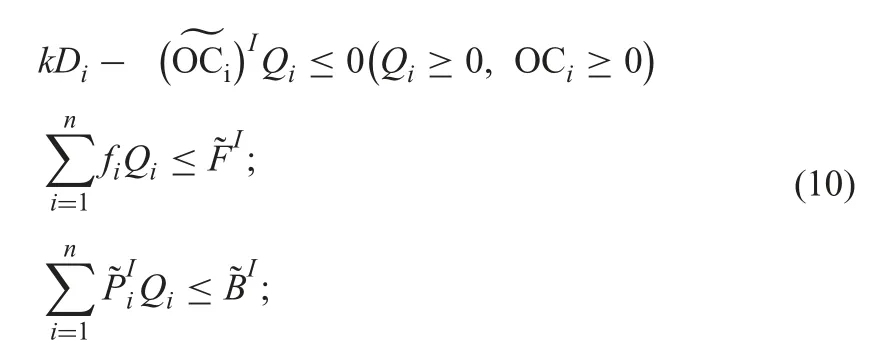
4 Solution methodology

In this section,we present a method to solve the model(10)which is based on‘possibility and necessity measures’.For it,we convert the model (10) into the deterministic problem under possibility and necessity measure.Then,the aim is to minimise the total holding cost and maximising the total profit under several constraints.Thus,based on it,the optimisation model becomes

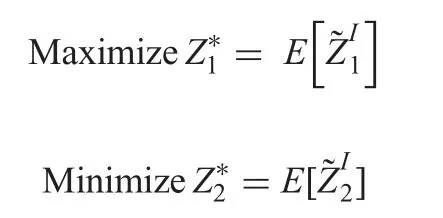
Subject to the constraint

Wherea&bare the predetermined confidence levels

After the fuzzification of the proposed model (10),the deterministic model is written in (11) form.The model (11) is a multi-objective problem,so we can’t solve this problem without transform to single-objective problem.Therefore,using fuzzy interactive satisfied method [13,14]we transformed a single objective problem as follows

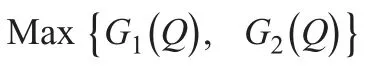
Subject to the constraint

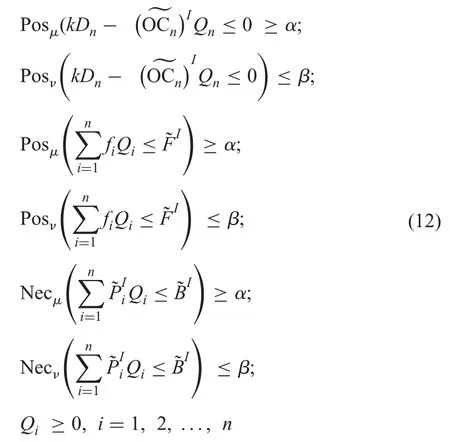
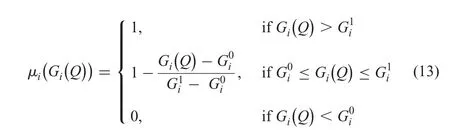
Subject to the constraint

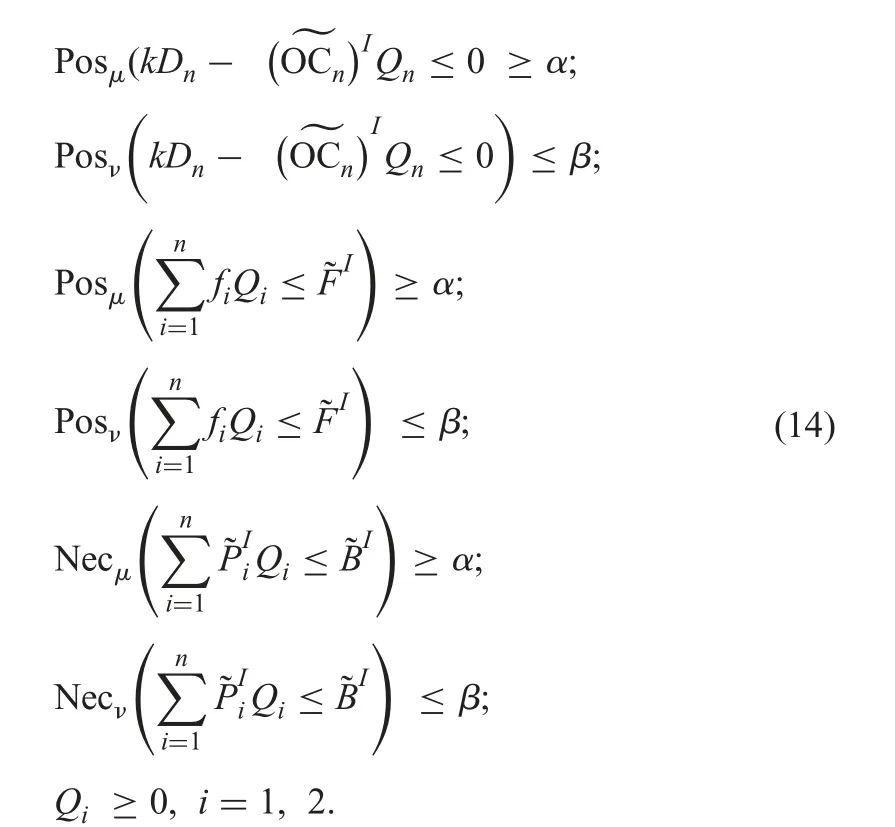
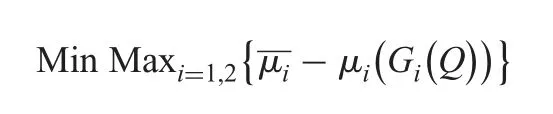
Subject to the constraint

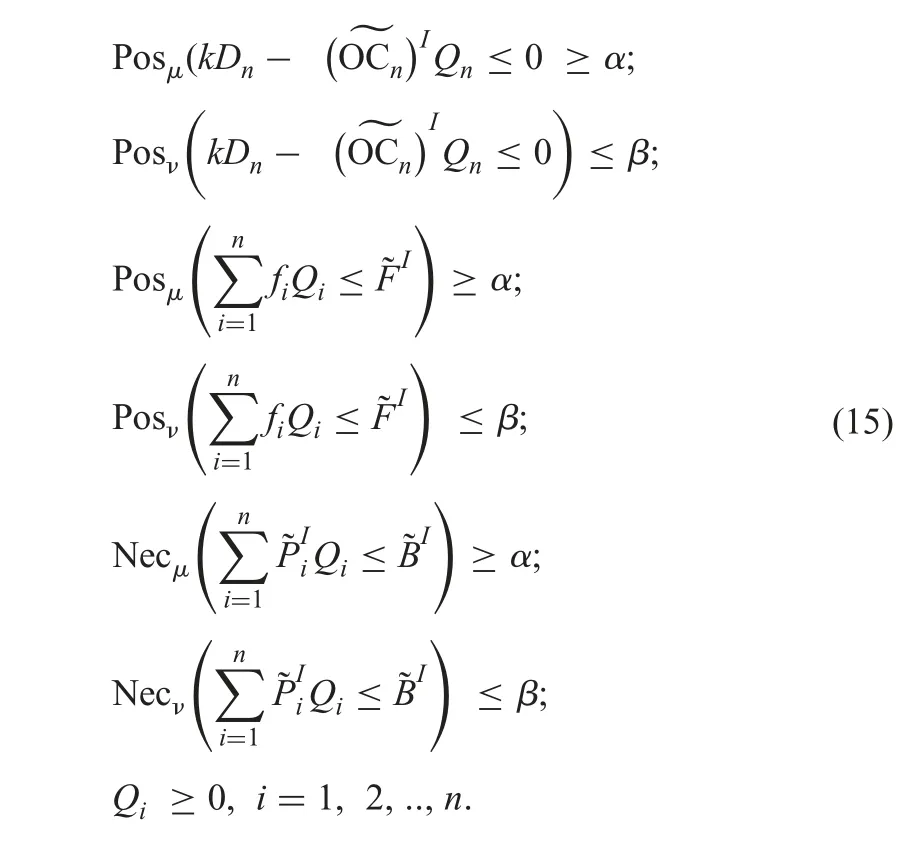
By proposing the auxiliary variableρ,problem(15)is equivalent to Minρ

Subject to the constraint

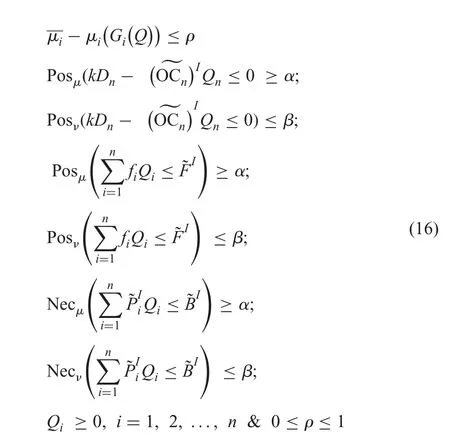
5 Numerical example

To illustrate the above-developed approach,we present an example taken from the inventory study.In it,we have taken all their parameters as a GIFN.The description of the problem is read as below.

A manufacturing company made some items and stock these items in a warehouse.The company required space for each item are f1=2,f2=4 and warehouse total floor area1050,1150;0.6)(950,1000,1050,1200;0.4)),total available budget is1100;0.4)),and fixed cost per order is k=8.In this problem,the holding cost depends on the quantity of storage and replenishment cost depends upon the amount of product produced in a length of the cycle.Similarly the ‘ordering cost’,‘selling cost’ and‘purchasing cost’ of the items that cannot be prefixed depend upon some situations.Therefore,the parameters of the inventory model holding cost,replenishment cost,ordering cost,selling cost,and purchasing cost of the items may be uncertain.Hence,the ‘total profit of the inventory’ in a length of cycle may be uncertain.These uncertainty captured by generalised intuitionistic parameters.The input generalised trapezoidal intuitionistic fuzzy parameters are summarised in Table 1.Now,we find the optimal order quantityandThen the optimal solution of the proposed problem presented in Table 2.

5.1 Comparative study

To show the validity of the proposed optimisation method,a comparative study has been done with Chakraborty et al.[28]method.Chakraborty et al.[28]proposed an expected value of fuzzy numbers.Here he discussed a solution method which is based on expected value.This solution technique is used when we transformed the fuzzy linear programming problem todeterministic problem.Using this method he transformed fuzzy multi-objective linear programming problem to deterministic problem.This method based on only expected value.However our proposed method based on expected value,possibility measures,and necessity measures.Our method is more realistic compared to Chakraborty et al.[28]method.When we applied the expected value method on our proposed fuzzy problem that time objective function as well constraints gives an average value.Therefore,we have used expected value,possibility measures,and necessity measures of the proposed problem that time gives better optimum result from Chakraborty et al.[28]method.

Table 1 Input generalised intuitionistic trapezoidal fuzzy parameters

Table 2 Optimal result for a=0.6, b=0.4

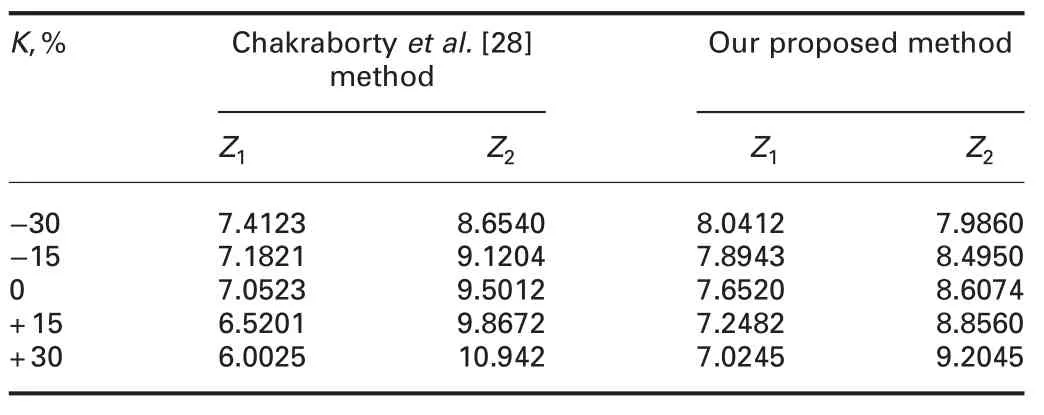
Table 3 Comparative sensitivity analysis with Chakraborty et al.[28]method

In this comparative study,we have considered the proposed numerical example with same input crisp parameters as well as intuitionistic fuzzy parameters (viz.Table 1).Here,k is the fixed cost parameter in the proposed mo del.This parameter plays a very important role to optimise profitand holding costof the proposed model.The advantage of our proposed optimisation method compared with Chakraborty et al’s.[28]method has been shown by sensitivity analysis.In Table 3 sensitivity analysis are performed with changes of ?30%,?15%,+15% and+30% in the key parameter (k) of the proposed problem.From Table 3,it is clear that our optimisation method gives the best result other than Chakraborty et al.[28]method for the generalised intuitionistic fuzzy LFI model.

6 Conclusion

As an eminent issue of IFSs,GIFNs are the consistent tools to fleet the fuzzy and uncertain quantities with hesitance degrees.GIFN are special kind IFS on the real number and is a viable tool to handle the uncertainties in a problem.In this paper,we have proposed a MOLF inventory model with GIFNs environment and minimise the holding cost and maximise the profit related to ‘per-ordered quantity’ under the different constraints.The formulated intuitionistic fuzzy optimisation model is transferred into its deterministic ones by employing possibility and necessity measures.In order to solve the model,we follow the fuzzy interactive method by assigning different goals of the decision makers to the model and hence solve it.Based on the study and assigning a different priority goal,a decision-maker can select their desired output and hence can change their plans to save money in the future.Also,the comparative study reveals that the proposed approach gives feasible results.In the future,we shall extend our method to some other uncertain environment and apply them on supply chain management and inventory problems using some hybrid soft computing techniques [29,30].