陜西省城固師范學(xué)校(723200) 劉敬民

而對于b2-4ac ≥0 時的函數(shù)值域問題采取回避的態(tài)度.實際上此法可擴(kuò)展適用于所有的二次分式函數(shù),在解題過程中要注意判斷是否為函數(shù)值及定義域?qū)瘮?shù)值的影響,檢驗Δ=0 時的情形.

判別式法又名方程法是用方程的觀點求解的,也就是把函數(shù)y = f(x)同解變形為x 的一元二次方程,利用Δ ≥0求得原函數(shù)的值域.此法不僅適用于分式函數(shù)而且適用于二次分式函數(shù),還適用于解析式中含有根號的情形.用此法求二次分式函數(shù)值域解題步驟和方法容易被學(xué)生掌握,但知其法不明算理的情況應(yīng)引起我們的重視和關(guān)注.

命題一如果二次分式函數(shù)中至少有一個不為零)的分子分母互素,那么關(guān)于x 的分式方程

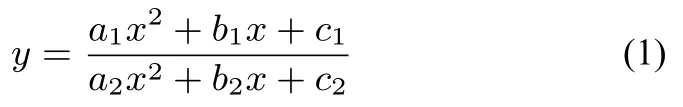
與關(guān)于x 的整式方程

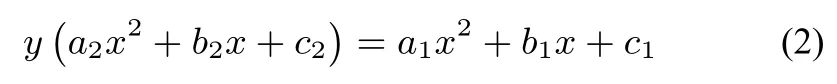
同解.

證明設(shè) x0是 (1) 方程的一個根, 即 y =由于有成立, 這說明x0也是方程(2)的一個根.

反過來, 設(shè)x0是方程(2) 的一個根, 即此時有b2x0+ c20, 否則有這樣a1x2+b1x+c1與a2x2+b2x+c2有公因式(x-x0),與已知分子分母互素矛盾.于是有成立.這說明x0也是方程的根.

因此,方程(1)與方程(2)是同解的.

2.分子分母互素的二次分式函數(shù)值域

命題二如果二次分式函數(shù)a20)的分子分母互素,那么

證明由命題一知方程與方程y(a2x2+b2x+c2)= a1x2+b1x+c1是同解的,進(jìn)一步有同解方程

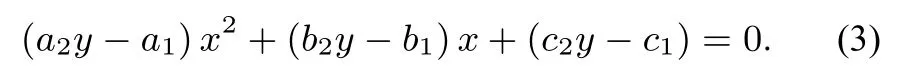
設(shè)a2y - a10, 因為x 是實數(shù), 故判別式非負(fù).即Δ = (b2y-b1)2-4(a2y-a1)(c2y-c1) ≥0,此時由同解變形方程(3)得到的每一個x 的值均有a2x2+b2x+c20,也就是說由解出的任意一個y 均為函數(shù)值.

設(shè)a2y-a1=0,此時a20 否則a1=0,a1,a2同時為零與已知矛盾.因而有當(dāng)即a1b2a2b1時, 由方程(3)得由于方程(1)(2)(3)同解, 有為相應(yīng)的函數(shù)值; 當(dāng)時,由于函數(shù)的分子分母互素,因此關(guān)于x 的方程(3)無解,不是函數(shù)值.

又a2y-a1= 0 時,Δ = (b2y-b1)2≥0 顯然成立,因此當(dāng)且a20 時,所求值域要從Δ ≥0 的解集中去掉

3.分子分母有公因式的二次分式函數(shù)值域

命題三如果二次分式函數(shù)a20) 的分子分母有唯一公因式(x - m), 那么函數(shù)的值域為Δ ≥ 0 的解集中去掉和后的部分, 即y =且和或y =

證明設(shè)x1和x2分別為方程a1x2+b1x+c1= 0 和a2x2+b2x+c2=0 的另外一個根且x1x2,于是函數(shù)y =即：可化為方程

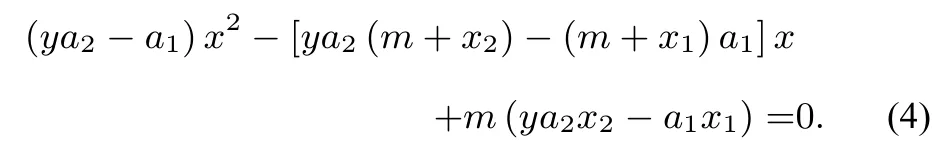
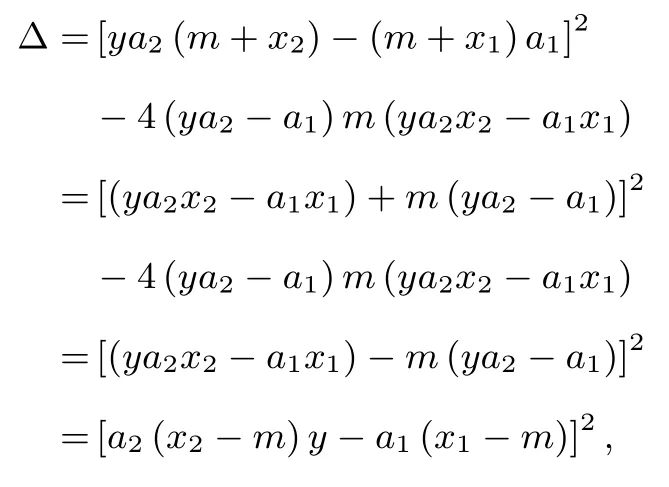
設(shè)ya2-a10,有于是當(dāng) Δ ＞ 0 時, 由方程 (4) 得 x =進(jìn) 一 步 有：x=或者x=m 增根;

當(dāng)Δ = 0 時, 即ya2x2- a1x2= (ya1-a1)m 等價于：a2(x2-m)y - a1(x1-m) = 0(x2m 時), y =此時是增根.也就是說Δ = 0, x2m 時方程(4) 有解而原函數(shù)的值不存在, 因此要從Δ ≥0 的解集中去掉

又, 當(dāng) x2= m 時, 由于 x1x2, Δ =[a2(x2-m)y-a1(x1-m)]2=而Δ ＞0 時, 不等式解集中y 均存在相應(yīng)的x(xx1和xm)使得y 為函數(shù)值.因此,x2=m 對于Δ ≥0 的解集沒有影響.

設(shè)ya2- a1= 0, 即由方程(4) 可得：a1(x2-x1)m = ma1(x2-x1), 由于a10,x1x2, 則x = m 為增根, 因此不是函數(shù)值.又ya2- a1= 0 時, Δ = [ya2(x2-m)-a1(x1-m)]2=[a1(x2-m)-a1(x1-m)]2=因此,要從Δ ≥0 的解集中去掉

4.小結(jié)與應(yīng)用舉例

以上分情形討論了用判別式法就求解二次分式函數(shù)值域時分子分母可能出現(xiàn)的各種情形,一言蔽之,倘若事先不去考慮各種可能的因素, 需要判斷是否為函數(shù)值以及Δ=0 時的檢驗.

例1求函數(shù)且x-3,x1)值域.

解由已知得yx2+ 2xy - 3y = x2- 2x + 3, 即(y - 1)x2+ 2(y + 1)x - 3(y + 1) = 0.當(dāng)y = 1 時, 得為函數(shù)值.當(dāng)y1 時,Δ=4(y+1)2+12(y+或y ≤-1.檢驗：時,x=3;y =-1 時,x=0.和y =-1 均為函數(shù)值.

例2求函數(shù)且x-3,x1)的值域.

解由已知得yx2+ 2xy - 3y = 2x2+ 4x + 1, 即(y-2)x2+2(y-2)x-3(y+1)=0.

(1) 當(dāng)y =2 時,得-7=0,x 不存在.因此,y =2 不是函數(shù)值.

例3求函數(shù)(x ∈R 且x3)值域.

解由題有xy-3y =x2-3x+2,即x2-(y+3)x+3y+2=0,有Δ=(y+3)2-4(3y+2)=y2-6y+1 ≥0,或檢驗：時,時,均為函數(shù)值.值域為

類似地,可以繼續(xù)用判別式法求下列分式函數(shù)值域.