孫蘇珍,王冬嶺

(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)

1 引言

經(jīng)典Schr?dinger方程是量子力學(xué)中的一個基本方程,也是量子力學(xué)的一個基本假定,它描述了微觀粒子的狀態(tài)隨時間變化的規(guī)律.半經(jīng)典量子力學(xué)界于經(jīng)典物理和量子物理之間,運用到了量子力學(xué)量子化的概念,但同時并沒有摒棄經(jīng)典物理中的一些理念,是經(jīng)典力學(xué)過渡到量子力學(xué)中的產(chǎn)物.在半經(jīng)典量子力學(xué)中,物質(zhì)運動狀態(tài)有一條近似的經(jīng)典軌跡,同時也會受到不可忽略的量子效應(yīng)擾動.從數(shù)學(xué)方程角度來看,由于單個粒子的狀態(tài)高度集中在某條近似經(jīng)典軌跡的附近,波函數(shù)會在局部形成強烈的高振蕩,即半經(jīng)典 Schr?dinger方程的解具有局部高振蕩特征.對于半經(jīng)典Schr?dinger方程的研究,文獻(xiàn)[1-7]在這方面做了很多工作.

整數(shù)階Laplace方程基于經(jīng)典的布朗運動假設(shè),分?jǐn)?shù)階Laplace方程基于粒子運動的 Lévy過程,Lévy過程有利于刻畫粒子的非局部特征,于是許多學(xué)者開始重視研究分?jǐn)?shù)階 Laplace方程.文獻(xiàn) [8]利用 Rieze位勢給出了 (??)s的定義,至此人們開始對分?jǐn)?shù)階Laplace方程展開了豐富的研究并獲得了大量成果.文獻(xiàn)[12]給出了分?jǐn)?shù)階Laplace算子基本解,為之后研究分?jǐn)?shù)階Laplace方程解的性質(zhì)奠定了基礎(chǔ).文獻(xiàn)[9]給出了(??)s的最大值原理,文獻(xiàn)[10]研究了分?jǐn)?shù)階Laplace方程解的正則性.目前,分?jǐn)?shù)階Laplace算子在自然科學(xué)領(lǐng)域已經(jīng)有了重要的應(yīng)用.分?jǐn)?shù)階導(dǎo)數(shù)是一個非局部算子,與整數(shù)階微分方程相比,能更好地描述具有長程效應(yīng)的物理現(xiàn)象和動態(tài)過程.

首先簡單介紹幾種分?jǐn)?shù)階Laplace的定義方法[11]:

(i)定義在Rn上的分?jǐn)?shù)Laplace算子是一個具有非局部性的擬微分算子,形式如下:

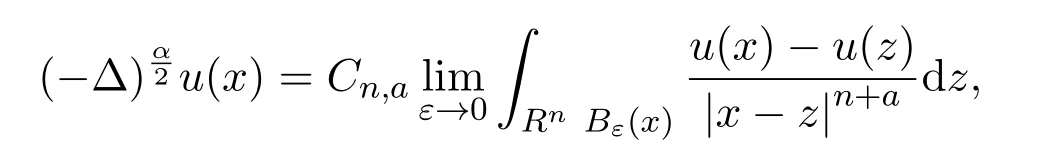
其中α∈(1,2)是任意實數(shù),Cn,a是依賴于空間維數(shù)n和α的常數(shù),該算子定義在S空間,即由Rn光滑速降函數(shù)構(gòu)成的Schwarz空間.

(ii)在S空間中,也可以用Fourier變換來等價地定義分?jǐn)?shù)階Laplace算子:

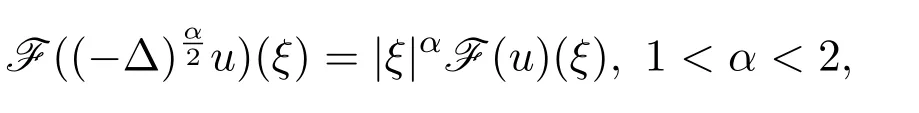
其中F(u)是u的Fourier變換.當(dāng)α=2時,分?jǐn)?shù)Laplace算子退化成經(jīng)典的Laplace算子,當(dāng)1<α<2時,該分?jǐn)?shù)階Laplace算子為非局部算子.

(iii)還可以將算子延拓到廣義函數(shù)空間

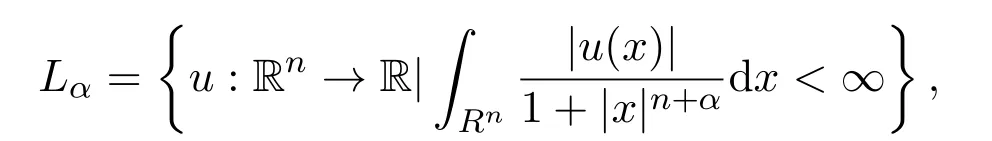
其中該空間內(nèi)積定義如下

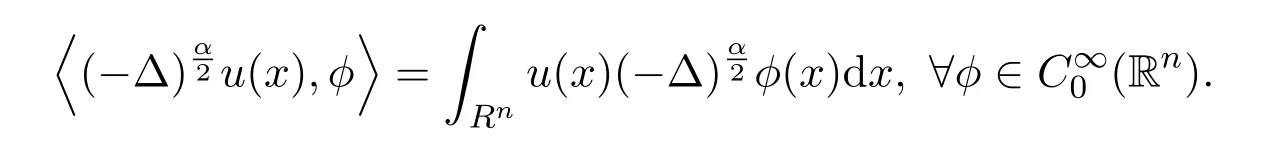
(iv)還可以通過考慮在Rn×[0,+∞)的以下問題來定義Laplace算子:

其中C=C(n,a)是一個合適的正常數(shù),詳見文獻(xiàn)[12].本文用Fourier變換來定義分?jǐn)?shù)階Laplace算子.

選擇譜方法(Galerkin譜方法[13]和擬譜方法[1-2])作為求解 Schr?dinger方程的首要數(shù)值方法,主要是因為譜方法有高精度,并且Schr?dinger方程本身具有譜算子特征.分裂算法是微分方程計算中常用到的一種方法,它將原方程分裂成幾個更簡單的方程,然后通過某種組合方式來構(gòu)造出原方程的數(shù)值算法.分裂算法和擬譜算法的結(jié)合,可以同時具備顯格式,高精度,保結(jié)構(gòu)的特點.由于Schr?dinger方程在空間方向是線性的,可以直接用譜方法進行空間離散變成線性常微分方程,并且勢函數(shù)可以精確求解,所以用分裂譜方法來求解Schr?dinger方程有很明顯的優(yōu)勢.

本文主要通過分裂譜算法把文獻(xiàn)[14]中關(guān)于半經(jīng)典整數(shù)階Schr?dinger方程解的高振蕩行為推廣到空間分?jǐn)?shù)階Schr?dinger方程,并通過數(shù)值比較研究空間分?jǐn)?shù)階階數(shù)α對解的高振蕩行為的影響.

2 整數(shù)階半經(jīng)典 Schr?dinger方程

考慮d(d≥1)維線性 Schr?dinger（LS）方程:

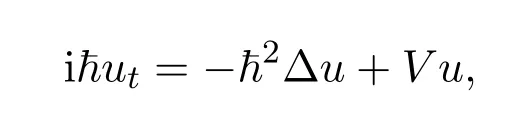
其中u=u(x,t)是關(guān)于空間變量x和時間變量t的波函數(shù),i是虛數(shù)單位,~是普朗克常數(shù),V=V(x)是勢函數(shù),(x,t)∈R+×?,??Rd是波函數(shù)在空間中的定義域.在線性 Schr?dinger方程中,當(dāng)常數(shù)很小時,即 0

半經(jīng)典的 Schr?dinger方程在許多應(yīng)用中起著核心作用,是量子力學(xué)的基本模型[15].具有時間依賴勢的Schr?dinger方程在量子物理學(xué)和理論化學(xué)中具有重要意義,考慮具有時間依賴勢的半經(jīng)典Schr?dinger方程的初值問題[14]

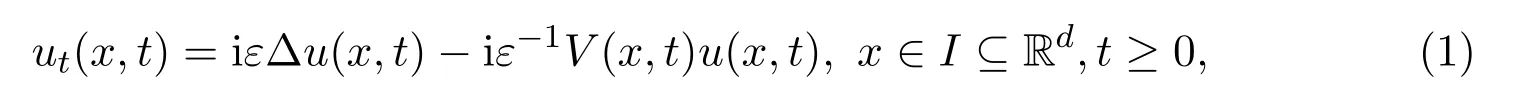
初值條件u(x,0)=u0(x),其中V是一個實值的,具有時間依賴的勢函數(shù),0<ε?1是半經(jīng)典參數(shù).

(1)式描述了一個由電子和一個更大質(zhì)量的粒子或粒子系統(tǒng)組成的系統(tǒng),例如原子核或原子晶格,具有相互作用勢V,ε是電子和質(zhì)量更大的系統(tǒng)質(zhì)量之比的平方根.由于方程(1)是線性的,可直接對空間變量半離散化,將其轉(zhuǎn)化為線性O(shè)DE方程,然后通過計算矩陣指數(shù)來求解.但其中半經(jīng)典參數(shù)ε的微小變化會引起解的快速震蕩,因此給數(shù)值離散帶來了很大的困難,解決這些困難既需要算法的靈活性也需要對原方程解的結(jié)構(gòu)進行一定的分析和理解.一個很好的方法是用分裂譜方法,因為Schr?dinger方程在空間方向是線性的,可以直接用譜方法進行離散變成線性方程,并且分裂譜方法對整數(shù)階和分?jǐn)?shù)階都有優(yōu)勢,從而避免了分?jǐn)?shù)階算子的非局部特征差分離散導(dǎo)致的滿矩陣帶來的計算量增加.

3 空間分?jǐn)?shù)階半經(jīng)典 Schr?dinger方程

4 數(shù)值試驗與分析

4.1 一維例子

根據(jù)上面的數(shù)值方法,首先考慮一維的數(shù)值例子,其中V(x)=2x2,初值條件

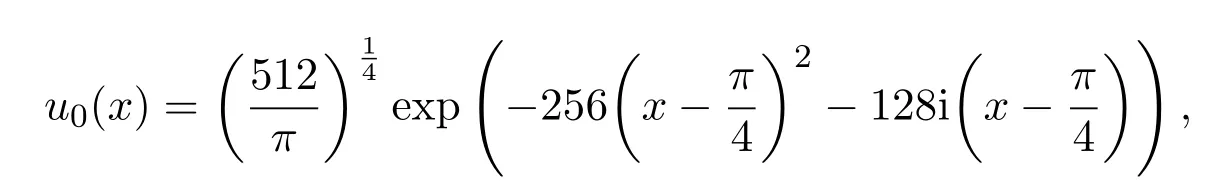
取x=[?π,π],N=1000,t=[0,0.5],M=500,通過分裂譜方法對空間分?jǐn)?shù)階半經(jīng)典 Schr?dinger方程進行數(shù)值計算,下圖為數(shù)值解u(x,t)及Re(u(x,t)),Im(u(x,t))的圖像,其中取各種參數(shù)ε,α進行比較分析.

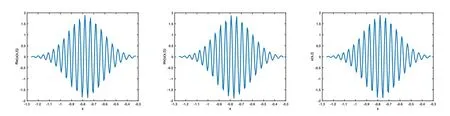
圖 1 取 ε=10?2,α=2時對應(yīng)的 Re(u(x,t)),Im(u(x,t),u(x,t)圖像

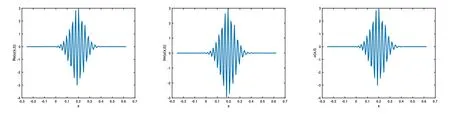
圖 2 取 ε=10?2,α=1.8時對應(yīng)的 Re(u(x,t)),Im(u(x,t),u(x,t)圖像

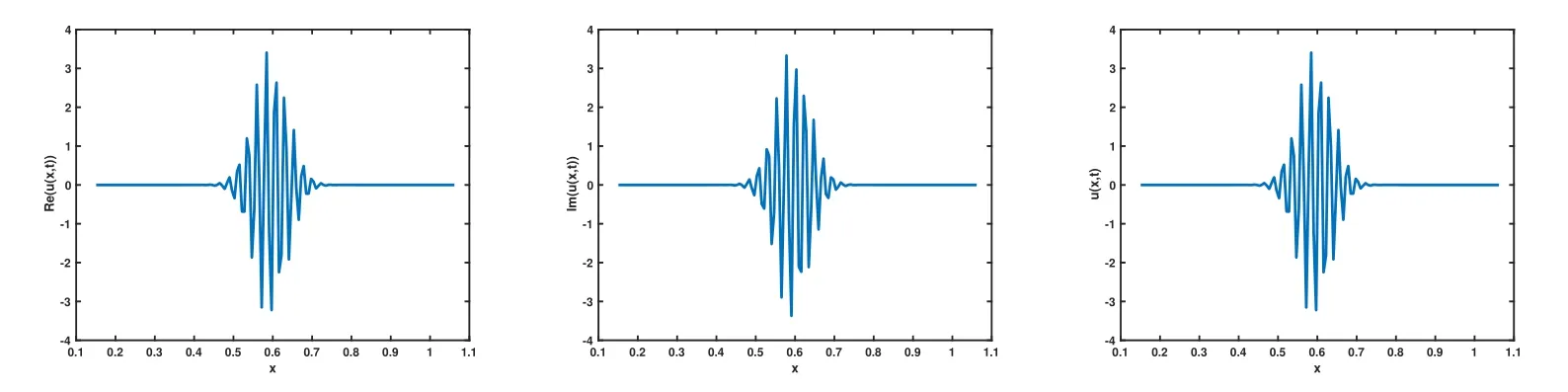
圖3 取ε=10?2,α=1.6時對應(yīng)的Re(u(x,t)),Im(u(x,t),u(x,t)圖像

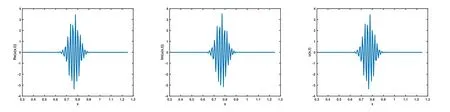
圖4 取ε=10?2,α=1.2時對應(yīng)的Re(u(x,t)),Im(u(x,t),u(x,t)圖像

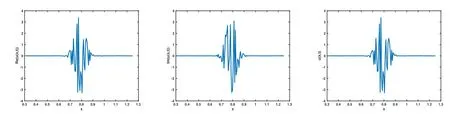
圖5 取 ε=10?4,α=2時對應(yīng)的 Re(u(x,t)),Im(u(x,t),u(x,t)圖像

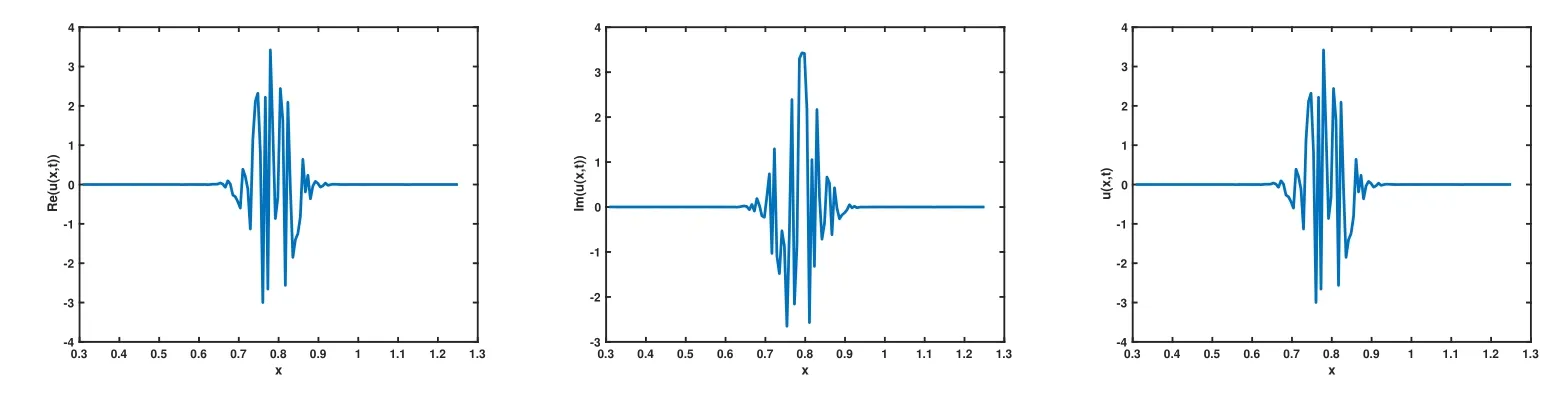
圖6 取ε=10?4,α=1.6時對應(yīng)的Re(u(x,t)),Im(u(x,t),u(x,t)圖像

從圖1-圖6可以看到,通過與整數(shù)階薛定諤方程的比較,當(dāng)α不斷變小時,波函數(shù)在空間方向的振蕩頻率增高,振蕩寬度變小,峰值變大.說明空間分?jǐn)?shù)階算子的階數(shù)α對于解的高振蕩特征具有明顯而直接的影響.空間分?jǐn)?shù)階算子的非局部特征具有使得解的振蕩聚集的效應(yīng).改變勢函數(shù)為V(x)=1+cos(x),其他條件和上面例子相同,分別取不同的α,對應(yīng)計算結(jié)果的圖像如下,從圖中不難發(fā)現(xiàn)和上面類似的結(jié)果,即空間分?jǐn)?shù)階算子對于解的高振蕩產(chǎn)生顯著的影響和聚集效應(yīng).

圖7 取ε=10?1,Re(u(x,t))在α=2,1.95,1.9的圖像

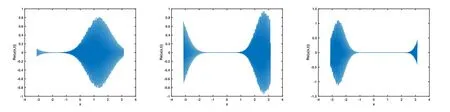
圖 8 取 ε=10?1,Re(u(x,t))在 α=1.85,1.8,1.75的圖像

圖 9 取 ε=10?1,Re(u(x,t))在 α=1.7,1.6,1.2的圖像

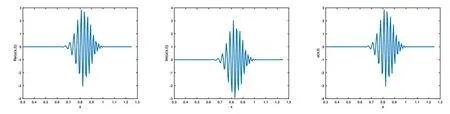
圖10 取 ε=10?3,α=2時對應(yīng)的 Re(u(x,t)),Im(u(x,t),u(x,t)圖像

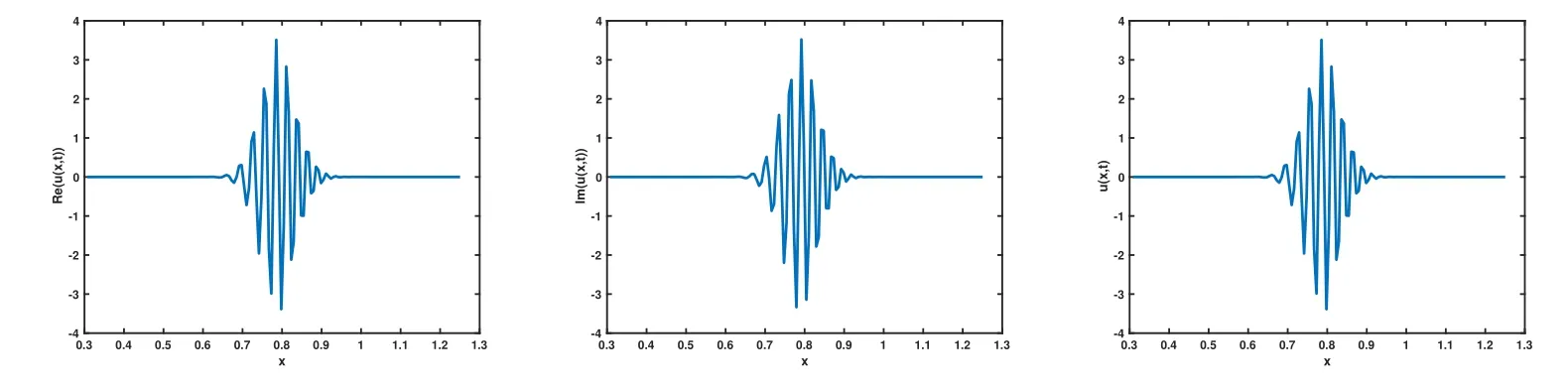
圖 11 取 ε=10?3,α=1.6時對應(yīng)的 Re(u(x,t)),Im(u(x,t),u(x,t)圖像

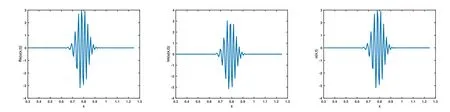
圖 12 取 ε=10?3,α=1.2時對應(yīng)的 Re(u(x,t)),Im(u(x,t),u(x,t)圖像

4.2 二維例子

進一步考慮二維空間分?jǐn)?shù)階半經(jīng)典Schr?dinger方程的例子

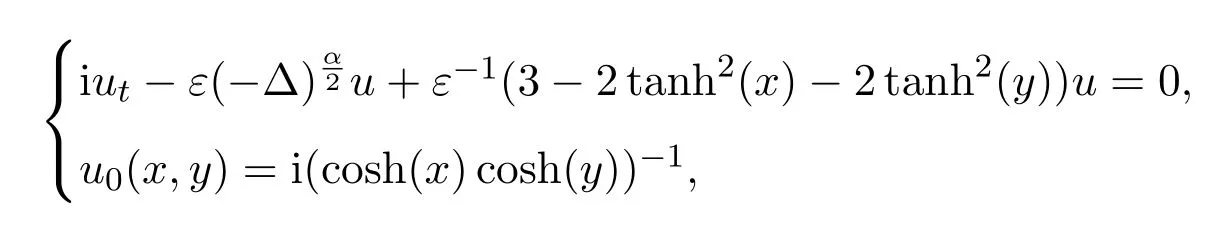
其中 ?=[?4π,4π]2×(0,T],取T=4,N=250,M=400,同樣用分裂譜方法對其進行數(shù)值計算,分別取α=2,1.6,1.2,下圖為數(shù)值解及其等高線圖像.

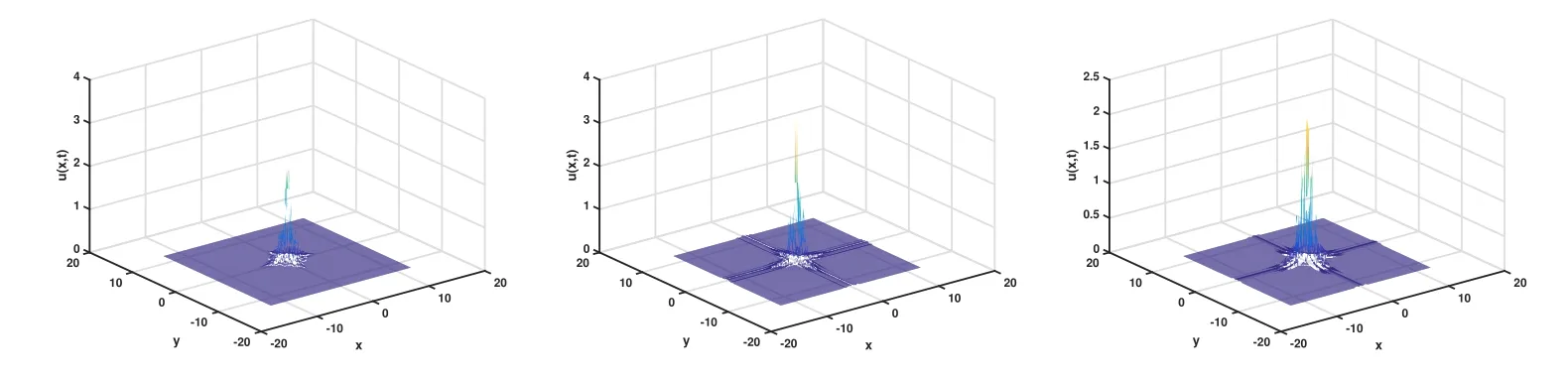
圖13 取 ε=10?1,u(x,t)在α=2,1.6,1.2的數(shù)值解

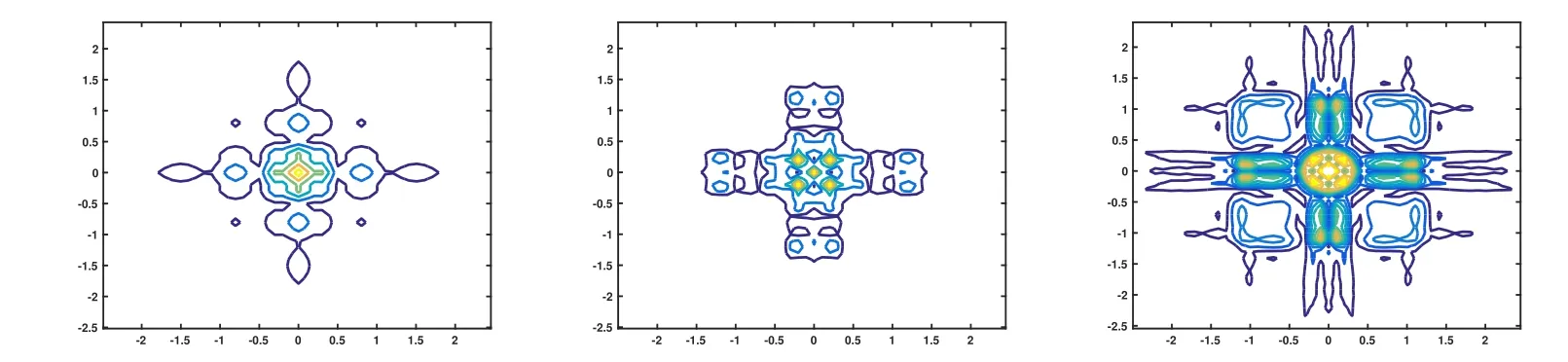
圖14 取ε=10?1,u(x,t)在α=2,1.6,1.2數(shù)值解的等高線圖

圖15 取 ε=10?2,u(x,t)在α=2,1.6,1.2的數(shù)值解

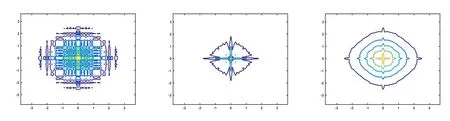
圖16 取ε=10?2,u(x,t)在α=2,1.6,1.2數(shù)值解的等高線圖

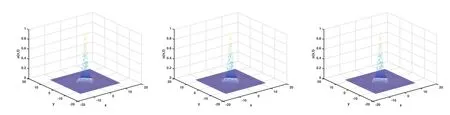
圖17 取 ε=10?6,u(x,t)在α=2,1.6,1.2的數(shù)值解

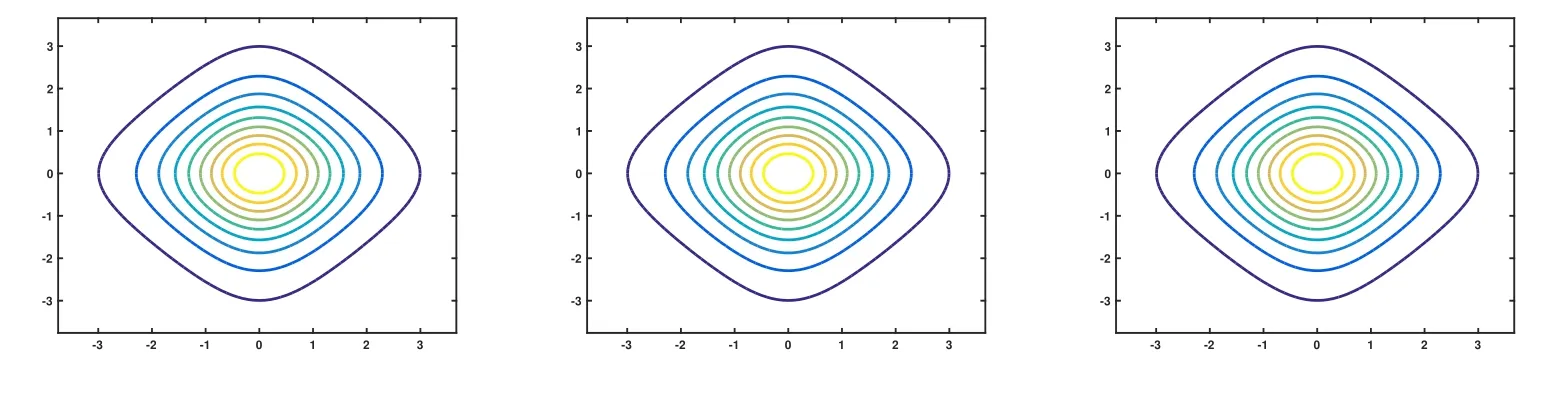
圖18 取ε=10?6,u(x,t)在α=2,1.6,1.2數(shù)值解的等高線圖

對于二維情況,從計算結(jié)果可以看出,空間分?jǐn)?shù)階算子對于解的振蕩也產(chǎn)生了明顯而直接的影響.當(dāng)參數(shù)ε相對較大時,空間分?jǐn)?shù)階算子對于解的振蕩的區(qū)域有著非常敏感的影響,隨著α的變小,振蕩區(qū)域開始擴散,振蕩的區(qū)域變大.但是當(dāng)參數(shù)ε相對較小時,空間分?jǐn)?shù)階算子對于解的振蕩的區(qū)域的敏感性降低,隨著α的變小,振蕩區(qū)域變小,振蕩特征逐步減弱,此時的分?jǐn)?shù)階算子表現(xiàn)出光滑效應(yīng),即逐步消除振蕩的效果.當(dāng)參數(shù)繼續(xù)變小取ε=10?6時,數(shù)值解基本上不再具有明顯的振蕩特征.