圓環(huán)上涉及重值及虧量的亞純函數(shù)的唯一性
2019-12-26 09:51:36譚洋
譚洋
(北京師范大學(xué)珠海分校應(yīng)用數(shù)學(xué)學(xué)院,廣東 珠海 519085)
1 引言
假設(shè)讀者熟悉亞純函數(shù)的Nevanlinna值分布理論[1-2].亞純函數(shù)的唯一性問題是值分布論中的一個重要研究課題,平面上亞純函數(shù)的唯一性問題已經(jīng)取得了豐碩的研究成果[3-5].文獻[6-7]將亞純函數(shù)的值分布理論推廣到多連通區(qū)域――圓環(huán).之后有學(xué)者研究了圓環(huán)上的亞純函數(shù)唯一性問題[8].本文主要研究了圓環(huán)上重值及虧量對亞純函數(shù)及其導(dǎo)數(shù)唯一性的影響,所得結(jié)果豐富了圓環(huán)上亞純函數(shù)的唯一性理論.
本文采用圓環(huán)上亞純函數(shù)Nevanlinna理論的符號[6-7].設(shè)f(z)與g(z)為兩個非常數(shù)亞純函數(shù),k為正整數(shù),a為任意復(fù)數(shù),如果f(z)?a與g(z)?a在計重數(shù)(不計重數(shù))之下具有相同的零點,則稱a為f(z)與g(z)的CM(IM)公共值.Ek(a,f)表示f(z)?a的所有k重零點的集合(計算重數(shù)).Ek)(a,f)表示f(z)?a的≤k重零點的集合(計算重數(shù));E(k(a,f)表示f(z)?a的>k重零點的集合.Ek(a,f)=Ek(a,g)表示f(z)?a的k重零點當且僅當是g(z)?a的k重零點.
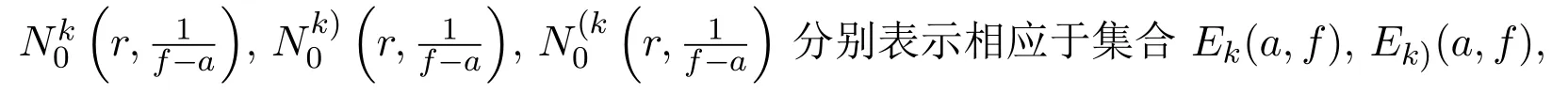

2 幾個引理





3 主要定理及證明
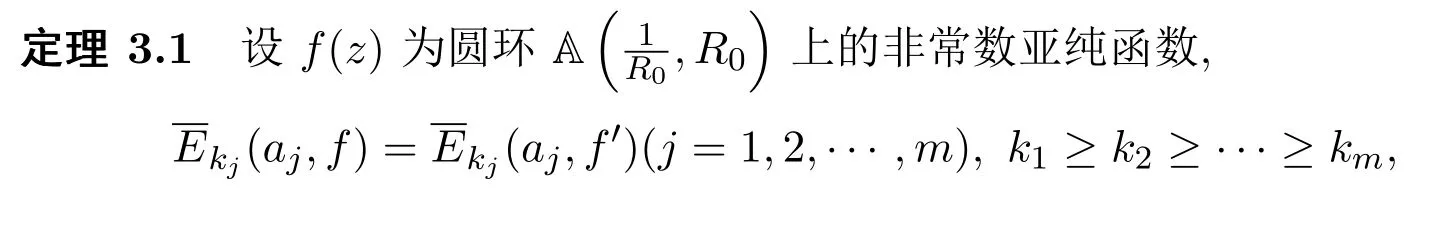







猜你喜歡
北京建筑大學(xué)學(xué)報(2022年1期)2022-03-29 03:16:30
大學(xué)數(shù)學(xué)(2022年1期)2022-03-21 12:59:52
北京建筑大學(xué)學(xué)報(2021年1期)2021-03-31 02:36:20
數(shù)學(xué)年刊A輯(中文版)(2019年2期)2019-05-20 09:53:08
數(shù)學(xué)物理學(xué)報(2019年1期)2019-03-21 05:26:12
數(shù)學(xué)年刊A輯(中文版)(2018年4期)2019-01-08 02:00:12
領(lǐng)導(dǎo)文萃(2015年13期)2015-08-03 03:14:56
油氣地質(zhì)與采收率(2014年5期)2014-11-28 05:35:38
數(shù)學(xué)年刊A輯(中文版)(2014年6期)2014-10-30 01:41:22
數(shù)學(xué)年刊A輯(中文版)(2014年2期)2014-10-30 01:40:58

