黃永峰 曹懷信 王文華

1) (陜西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院, 西安 710119)

2) (昌吉學(xué)院數(shù)學(xué)系, 昌吉 831100)

3) (陜西師范大學(xué)民族教育學(xué)院, 西安 710119)

傳統(tǒng)量子系統(tǒng)的哈密頓是自伴算子, 哈密頓的自伴性不僅保證系統(tǒng)遵循酉演化和保持概率守恒, 而且也保證了它自身具有實的能量本征值, 這類系統(tǒng)稱為自伴量子系統(tǒng).然而, 確實存在一些物理系統(tǒng)(如 PT ?對稱量子系統(tǒng)), 其哈密頓不是自伴的, 這類系統(tǒng)稱為非自伴量子系統(tǒng).為了深入研究 PT ?對稱量子系統(tǒng), 并考慮到算子 PT 的共軛線性性, 首先討論了共軛線性算子的一些性質(zhì), 包括它們的矩陣表示和譜結(jié)構(gòu)等; 其次,分別研究了具有共軛線性對稱性和完整共軛線性對稱性的線性算子, 通過它們的矩陣表示, 給出了共軛線性對稱性和完整共軛線性對稱性的等價刻畫; 作為應(yīng)用, 得到了關(guān)于 PT ?對稱及完整 PT ?對稱算子的一些有趣性質(zhì), 并通過一些具體例子, 說明了完整 PT ?對稱性對張量積運算不具有封閉性, 同時說明了完整 PT ?對稱性既不是哈密頓算子在某個正定內(nèi)積下自伴的充分條件, 也不是必要條件.

1 引 言

傳統(tǒng)的量子力學(xué)中, 量子系統(tǒng)的狀態(tài)隨時間的演化由一個自伴哈密頓量 H 決定的薛定諤方程來描述.哈密頓量的自伴性保證了系統(tǒng)遵守酉演化,同時也保證了其特征值為實數(shù).但是, 確實存在一些物理系統(tǒng), 其哈密頓不是自伴的, 但也具有實的能量本征值.Bender等[1?3]討論了哈密頓量H=p2+x2(ix?)?譜的性質(zhì), 其中 ? 為實數(shù), 說明了當(dāng)?≥0時其特征值都是實數(shù), 當(dāng) ? ＜0 時會出現(xiàn)復(fù)特征值, 從而提出了一類非自伴哈密頓, 稱為 PT ?對稱哈密頓.其中 P 是一個線性算子, 表示宇稱變換,T 是共軛線性算子, 表示時間反演變換.由于 PT ?對稱哈密頓的特征值為實數(shù)或者共軛成對出現(xiàn)的復(fù)數(shù), 為了保證其特征值為實數(shù), 又引入了完整PT ?對稱的概念.在此基礎(chǔ)上, 通過引入一個 C 算子, 構(gòu)造了一個新的正定 C PT ?內(nèi)積, 使得哈密頓H在該內(nèi)積下是自伴的, 從而也遵守酉演化, 同時還說明了 C 算子是不唯一的[4?7].后來, Mostafa?zadeh[8?12]提出了偽自伴算子的概念, 研究了偽自伴哈密頓的相關(guān)性質(zhì), 指出 PT ?對稱哈密頓可以看成一類特殊的偽自伴哈密頓, 同時給出了針對Freedman?Robertson?Walker模型中哈密頓是偽自伴的例子.Bender等[13]發(fā)現(xiàn)在 PT ?對稱量子理論下, 量子系統(tǒng)的最優(yōu)演化時間能夠迅速減小甚至達(dá)到零.Zheng等[14]通過設(shè)計核磁共振量子系統(tǒng)中具有 PT ?對稱哈密頓量的時間演化實驗, 證實了相應(yīng)的結(jié)果.目前, 關(guān)于 PT ?對稱量子理論的研究已經(jīng)涉及到了物理學(xué)及信息學(xué)的各個方面, 包括PT ?對稱性在光學(xué)領(lǐng)域的應(yīng)用[15], PT ?對稱量子場論的相關(guān)問題[16,17], PT ?對稱量子系統(tǒng)中的糾纏問題[18], PT ?對稱量子系統(tǒng)中無信號原理及其實驗觀測[19,20], PT ?對稱性與圖論及量子隨機游走的關(guān)系[21?23]等.此外, 還有一些其他的相關(guān)研究[24?37].最近, Huang等[38]通過弱測量模擬了缺破(broken) PT ?對稱哈密頓系統(tǒng).

本文首先討論共軛線性算子的一些性質(zhì), 包括其矩陣表示和譜結(jié)構(gòu); 其次, 給出線性算子的共軛線性對稱性和完整共軛線性對稱性的定義, 討論共軛線性對稱算子和完整共軛線性對稱算子所具有的相似Jordan標(biāo)準(zhǔn)型, 同時給出共軛線性對稱算子和完整共軛線性對稱算子的等價刻畫; 作為應(yīng)用, 得到非自伴哈密頓算子 PT ?對稱性及完整 PT ?對稱性的一些性質(zhì), 通過完整 PT ?對稱哈密頓的一些具體例子, 說明完整 PT ?對稱性對張量積不具有封閉性, 同時說明完整 PT ?對稱性既不是哈密頓算子在某個正定內(nèi)積下自伴的充分條件, 也不是必要條件.

2 共軛線性算子的性質(zhì)

本文用 K 表示 n 維復(fù) Hilbert空間, 用 ∥ x∥ 表示向量 x ∈K 的范數(shù), 即用 I 表示K 上的恒等算子.對于 K 上的線性算子 A , 用 A?表示線性算子 A 的Hermitian伴隨算子.若 A =A?,則稱 A 是自伴的; 否則, 稱 A 是非自伴的.若存在可逆線性算子 B 使得 A =B?B , 則稱 A 為正定算子;若 [ A ,B]:=AB-BA=0 , 則稱算子 A 與 B 可交換.

用 Mn(C) 表示全體n階復(fù)矩陣構(gòu)成的 C??代數(shù), In表示 n 階單位矩陣.用表示 a ∈C 的復(fù)共軛, 對對 A ,B∈Mn(C) , 若存在可逆矩陣 S ∈Mn(C) 使得 S-1AS=B , 則稱A相似于B, 記為 A ～B .如果矩陣A 相似于某個對角矩陣, 那么稱A可相似對角化.

定義1對于算子 A :K→K , 若

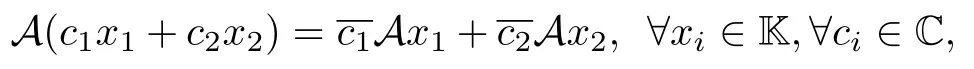
則稱 A 為共軛線性算子.

對于空間 K 上的任一共軛線性算子 A , 任取K的一個正規(guī)正交基令則

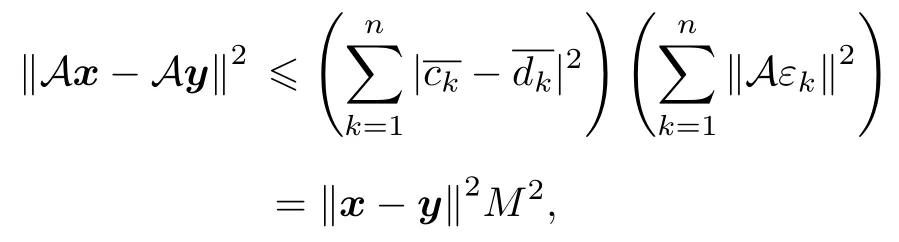
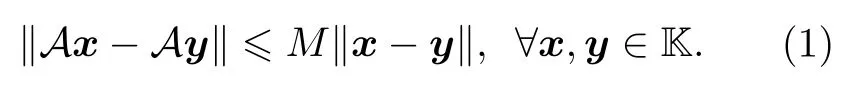
進(jìn)而可知, 空間 K 上的任一共軛線性算子 A 都是一致連續(xù)的.

通常, 任一 n ×n 階矩陣 A =[aij]n×n 都對應(yīng)空間 K 上的一個線性算子：

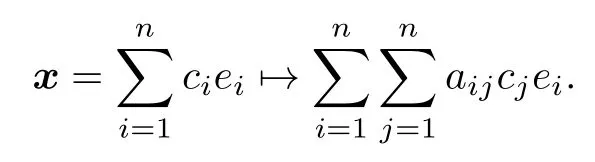
如果定義

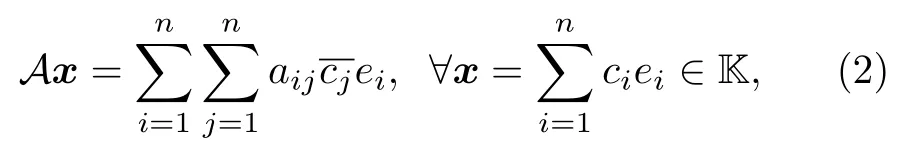
那么得到 K 上的共軛線性算子 A , 且滿足Aej=將此關(guān)系記為

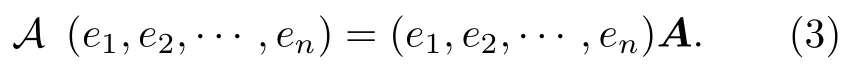
反之, 對 K 上任一共軛線性算子 A , 記

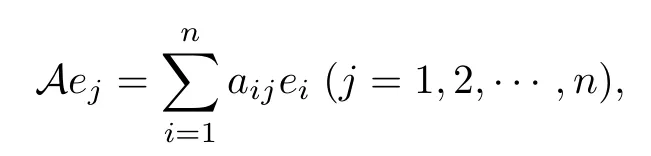
則得到一個 n ×n 矩陣 A =[aij] , 稱其為共軛線性算子 A 在基 E 下的表示矩陣.顯然, 算子 A 與其表示矩陣A滿足(3)式的關(guān)系, 從而表示矩陣A按照(2)式定義的算子正好為 A .

這說明, 共軛線性算子 A 與矩陣A在關(guān)系式(3)下是一一對應(yīng)的, 且 對任意有

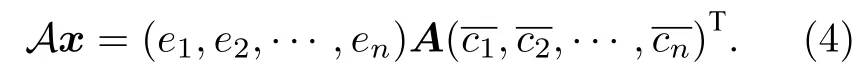
易見, 矩陣A為共軛線性算子 A 在基 E 下的表示矩陣當(dāng)且僅當(dāng)它們滿足關(guān)系式 (4).

定義 K 上的算子 T0為

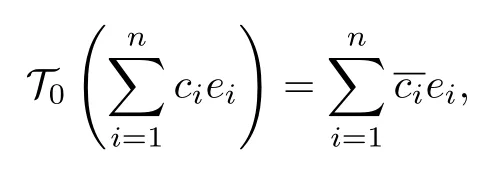
簡記為 T0x=.易見, T0是共軛線性算子, 且它在基 E 下的表示矩陣為n階單位陣 In.于是, 對任意有

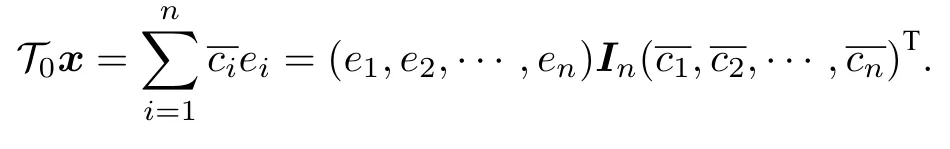
容易看出, 任何兩個共軛線性算子 A 與 T0的復(fù)合算子 T0A 或 A T0都為線性算子, 且滿足關(guān)系A(chǔ)=(AT0)T0=T0(T0A).由此可見, 任意一個共軛線性算子都可以看成是一個線性算子與 T0的復(fù)合,也可以表示為 T0與一個線性算子的復(fù)合.參見圖1.

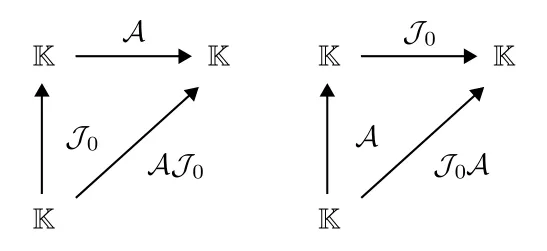
圖1 共軛線性算子 A 與 T0 的復(fù)合算子 A T0 (左)與T0A(右)都是線性算子, 且滿足關(guān)系A(chǔ)=(AT0)T0=T0(T0A)Fig.1.Composition operators A T0 (left) and T0A (right),composed of conjugate linear operators A and T0 , which are linear operators and satisfy A =(AT0)T0=T0(T0A) .

設(shè) A ,B 均為共軛線性算子, A ,B 為它們的表示矩陣, 則由 (4) 式知：對任意有

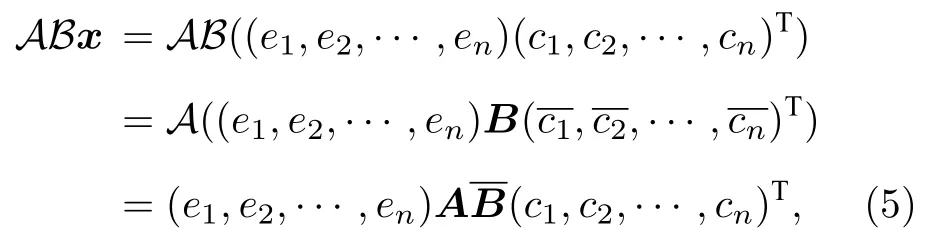
進(jìn)一步, 可以討論更一般的情形.設(shè)Ai(i=1,2,···,m)均為共軛線性算子,Ai(i=1,2,···,m)為對應(yīng)的矩陣表示, 則當(dāng) m =2k 為偶數(shù)時,A1A2···Am為 線 性 算 子, 其 矩 陣 表 示 為當(dāng) m =2k+1 為 奇 數(shù) 時 ,A1A2···Am為共軛線性算子, 其矩陣表示為

用 σ (A) 表示算子 A 的所有 特 征 值之集, 稱為A的譜, 即

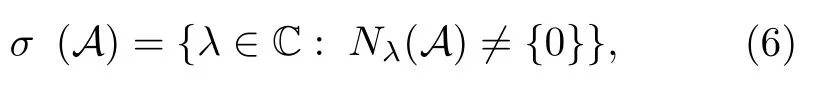
其中, Nλ(A)=ker(λI-A) , 稱為算子 A 對應(yīng)特征值 λ 的特征子空間.

例如, σ (I)={1} .由于

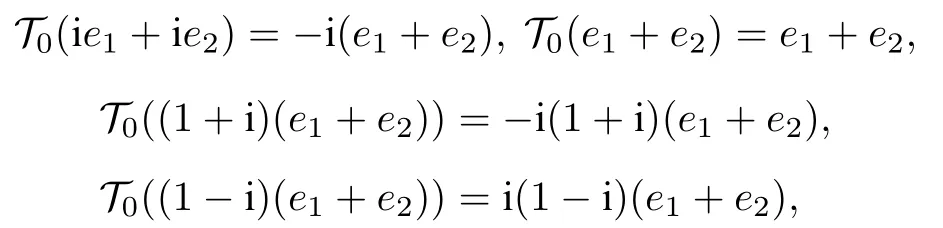
所以, σ (T0)? {-1,1,-i,i} .

下面討 論 一 般 共 軛線性算子 A 的譜 σ (A) 的一些性質(zhì).

首先, 由定義式(6)知, λ ∈ σ(A) 當(dāng)且僅當(dāng)算子方程 A x=λx 有非零解當(dāng)且僅當(dāng)矩陣 方 程 λ c=Acˉ 有 非 零 解 c =(c1,c2,···,cn)T; 此時, λ 稱為算子 A 的特征值, 相應(yīng)的非零解x稱為對應(yīng)于特征值 λ 的特征向量.

因此, 共軛線性算子 A 的譜 σ (A) 為復(fù)平 面上的一個有界集, 但可能為無限集(見定理1), 也可能為空集(見例1).

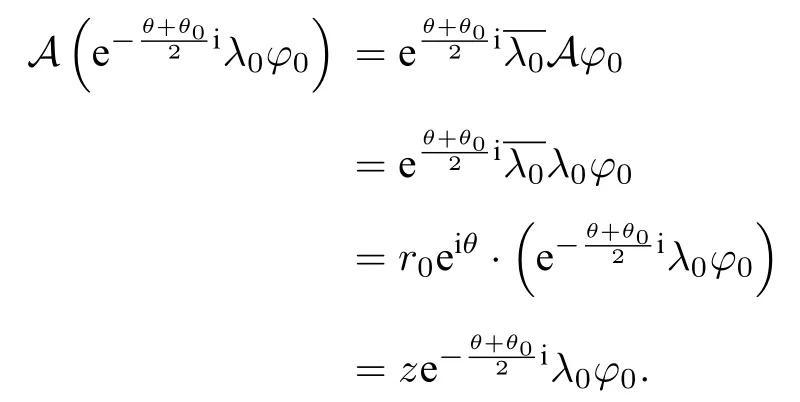
通過上面的討論, 可以得到下面的定理.

定理1設(shè) A 為 K 上的共軛線性算子, 其表示矩陣為A, 則

(a) λ 為 A 的特征值且有實的特征向量x當(dāng)且僅當(dāng) λ 為A的特征值且有實的特征向量c;

(b) 當(dāng) λ ∈ σ(A) 時, 有 | λ |2∈ σ(A2) ;

(c) A 的譜半徑滿足

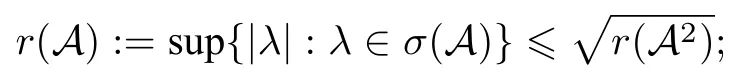
(e) σ (A) 為復(fù)平面上的有界閉集.

定理1說明了與線性算子的譜結(jié)構(gòu)不同：線性算子的譜為復(fù)平面上的有限集, 但共軛線性算子可能包含一系列以原點為公共圓心的圓周.其次, 由定理1中的結(jié)論 (b)知：當(dāng) σ (A2)∩(0,+∞)=? 時,必有 σ (A)=? (例1).于是, 如果線性算子 A2沒有正的特征值, 那么共軛線性算子 A 就沒有特征值.進(jìn)一步, 由于 σ (T0)? {-1,1,-i,i} 且所以由定理1(c)與定理1(d)知

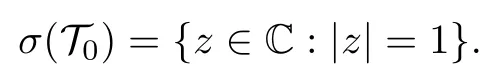
例 1設(shè) K 為 2 維復(fù)線性空間, { e1,e2} 為 K 的一組線性無關(guān)基, ? z∈ C , 定義算子 Az為

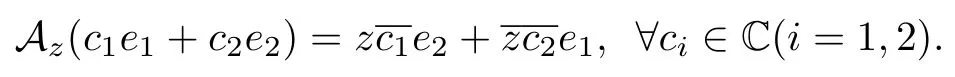
顯然, Az為 K 上的共軛線性算子, 且其表示矩陣為

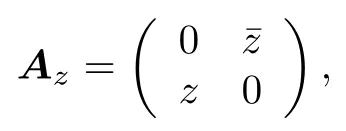
這里的算子 Ai正好為物理上的自旋 1 /2 ?粒子的翻轉(zhuǎn)算子, 它沒有特征值.

3 線性算子的共軛線性對稱性

下面討論共軛線性對稱算子的性質(zhì), 給出其表示矩陣具有的相似Jordan標(biāo)準(zhǔn)型.在此基礎(chǔ)上,討論完整共軛線性對稱哈密頓的性質(zhì), 給出完整共軛線性對稱性的等價刻畫.

定義2設(shè) H 為 K 上的線性算子, 若存在可逆的共軛線性算子 A , 使得 [ A ,H]=0 , 則稱 H 為共軛線性對稱的; 此時, 也稱 H 為 A ?對稱的.

為了討論共軛線性對稱算子的性質(zhì), 先給出以下引理.

引理1[39]設(shè) H ∈Mn(C) , 則H相似于 H 當(dāng)且僅當(dāng)H相似于某個實矩陣.

引理2[39]設(shè) H ∈Mn(C) , 則H相似于某個實矩陣當(dāng)且僅當(dāng)H相似于如下的標(biāo)準(zhǔn)型矩陣

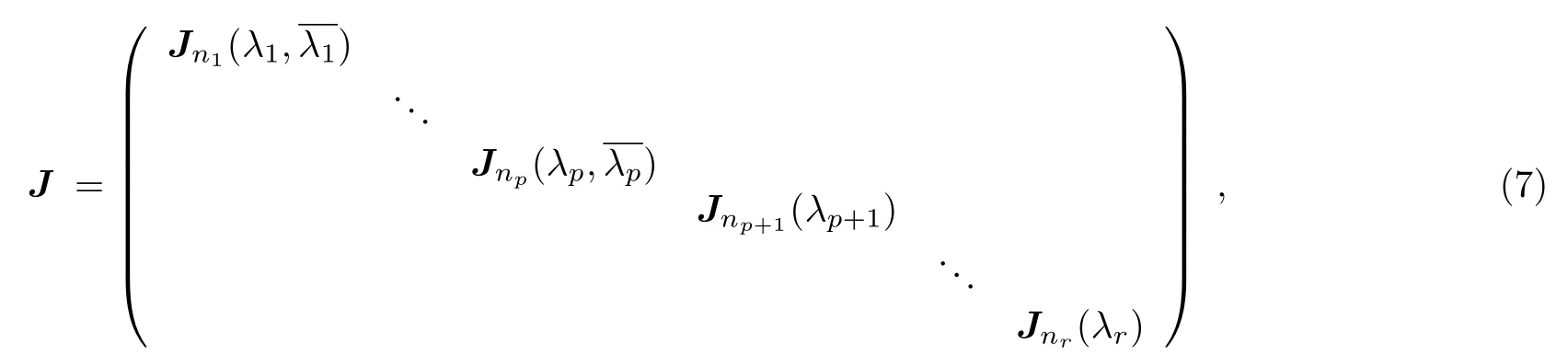
其中

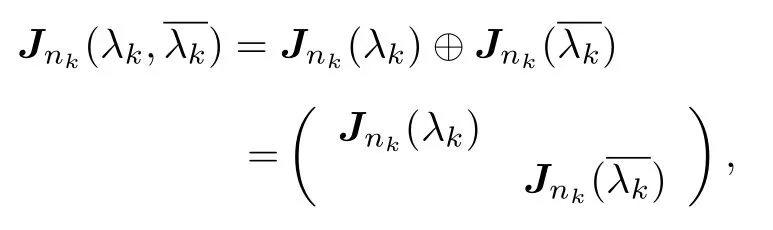
k=1,2,···,p;Jnk(λk)為標(biāo)準(zhǔn)Jordan塊,λ1,···,λp為非實數(shù)的復(fù)數(shù), λnp+1,···,λnr是實數(shù).

引理3[39]設(shè) A ∈Mn(C) , 則A滿足A=I當(dāng)且僅當(dāng)存在可逆矩陣 S ∈Mn(C) , 使得A=S-1.

下面的定理給出了共軛線性對稱算子的一些等價刻畫.

定理2設(shè) H 為 K 上的線性算子, 則以下敘述等價：

(i) H 是共軛線性對稱的;

(iii) H 的表示矩陣H相似于某個實矩陣;

(iv) H 的表示矩陣H具有相似Jordan標(biāo)準(zhǔn)型(7)式;

(v) 存在共軛線性算子A 滿足 A2=I , [ A ,H]=0 ;

(vi) 存 在 K 上 的 可 逆 線 性 算 子 η , 使 得H?= ηHη-1;

(vii) 存在 K 上的可逆自伴線性算子 η1, 使得(即 H 為 η1?偽自伴[37]).

證明(i) ? (ii).設(shè) H 是共軛線性對稱的, 則由定義 2 知, 存在共軛線性算子 A 使得 H 為 A ?對稱.記H和A分別為 H 和 A 的矩陣表示, 則有A=HA, 即=A-1HA .由 A 可逆知 A 可逆, 從而知H相似于.

由引理1可知 (ii)和(iii)等價, 由引理2可知(iii)和(iv)等價.

由定義2, 顯然(v) ? (i)成立.下面證明(i)?(v).

(i) ? (v).設(shè) H 為共軛線性對稱的, 則由引理1知, H 的表示矩陣H相似于某個實矩陣, 即存在可逆矩陣S使得從而令則同時由引理3知 A A=I .設(shè) A 為A所對應(yīng)的共軛線性算子, 則有 A2=I , 且 [ A ,H]=0 .

(ii) ? (vi).設(shè) H 為 H 的表示矩陣, 且相似于H.從而存在可逆矩陣A, 使得=AHA-1.又因為任意復(fù)矩陣的轉(zhuǎn)置矩陣與其本身相似, 從而存在可逆矩陣S使得即H?=設(shè)H,η為分別對應(yīng) H ,SA 的線性算子, 則有 H?= ηHη-1.

(vi) ? (ii).設(shè)存在 K 上的可逆線性算子 η , 使得 H?= ηHη-1.記 H ,A 為分別對應(yīng) H ,η 的表示矩陣, 則A為可逆矩陣, 且 H?=AHA-1.又因為H?和相似, 從而存在可逆矩陣S, 使得H?=因此從而=SA×H(SA)-1, 即H相似于.

顯然(vii) ? (vi)成立.下面證明(vi) ? (vii).

(vi) ? (vii).設(shè) H?= ηHη-1, η 為可逆線性算子.對非零的 a =reiθ∈ C , - e2iθ∈/σ(η-1η?) ,η0=aη仍為可逆線性的, 且有從而令 η1= η0+, 則 η1為自伴的 且因為所以從而可逆.又因為所以 η1可逆.由此, 證明了 η1為可逆自伴線性算子, 且證畢.

由定理2及引理2知, 共軛線性對稱算子的特征值都是實的, 或共軛成對出現(xiàn)的, 且共軛成對的特征值具有相同的代數(shù)重數(shù)和幾何重數(shù).在物理上, 一般希望可觀測量對應(yīng)的測量結(jié)果是實數(shù), 這就要求量子系統(tǒng)的哈密頓 H 的特征值均為實的.于是, 我們引入下面的完整共軛線性對稱的概念.

定義 3若 H 為空間 K 上的 A ?對稱線性算子,并且 H 的特征態(tài)均為 A 的特征態(tài), 則稱 H 為完整 A ?對稱的; 若存在可逆共軛線性算子 A 使得 H 為完整A ?對稱的, 則稱 H 為完整共軛線性對稱的.

下面說明具有完整共軛線性對稱的算子, 其特征值均為實數(shù).

命題 1設(shè) H 為 K 上的線性算子, 若 H 為完整共軛線性對稱, 則 H 的特征值都是實的.

證明設(shè)存在可逆的共軛線性算子 A , 使得AH=HA , 且 H 的 特 征 態(tài) 均 為 A 的 特 征 態(tài) .設(shè)a是 H 的一個特征值, 對應(yīng)的特征態(tài) f0 , 滿足Hf=af .因此, H Af=AHf=Af .由于 f也是A 的一個特征態(tài), 所以存在b使得 A f=bf .從而有 a bf=bf .因為 A 可逆, 故 b0 .又 f0 , 所以 a =證畢.

上述定理說明, 算子的完整共軛線性對稱性是其特征值為實數(shù)的充分條件, 但這并不是必要條件(見定理3).下面給出完整共軛線性對稱的一個等價刻畫.

定理3設(shè) H 是 K 上的線性算子且為共軛線性對稱的, 則 H 為完整共軛線性對稱的當(dāng)且僅當(dāng)H的特征值均為實的且 H 為非簡并的(即 H 的每個特征值的幾何重數(shù)為1).

證明必要性.設(shè) H 為完整共軛線性對稱, 由命題1知 H 的特征值都是實的.下面只需證明?a∈ σ(H), 有 d imNa(H)=1 .假設(shè) d imNa(H)＞1 ,則存在 K 中的兩個非零向量 x ,y 使得Hx=ax,Hy=ay 且 { x,y} 是線性無關(guān)集.由于 H 為完整共軛線性對稱, 所以存在可逆的共軛線性算子 A 以及c,d0使得 A x=cx,Ay=dy .當(dāng) cd 時, 取 z =x+y , 顯然它是 H 關(guān)于a的一個特征態(tài), 但是對于所有的復(fù)數(shù) λ , 都有 A z=Ax+Ay=cx+ d yλz .當(dāng) c =d 時, 取 z =x+iy , 顯然它是 H 關(guān)于 a 的一個特征態(tài), 但對于所有的復(fù)數(shù) λ , 都有Az=AxiAy=cx-icyλz .以上兩種情況下, 結(jié)果都與H具有完整共軛線性對稱性矛盾.由此可知 H 的每個特征值幾何重數(shù)均為1.

充分性.設(shè) H 的特征值均為實的且 H 非簡并.由于 H 為共軛線性對稱, 因此存在可逆的共軛線性算子 A 使得 H 為 A ?對稱, 只需證 H 的特征向量均為 A 的特征向量.設(shè) x =0 為 H 的對應(yīng)于 λ 某個特征向量, 則 λ 為實數(shù), 且使得 H x=λx .因為HAx=AHx=A(λx)=Ax= λAx , 即 A x 也為 H 對應(yīng)于特征值 λ 的特征向量.又因為 d imNλ(H)= 1, 從而存在 k0 使得 A x=kx , 即 x 為 A 的特征向量, 從而 H 為完整 A ?對稱的.證畢.

通過定理3可以得到下面的推論.

推論1K 上的線性算子 H 為完整共軛線性對稱當(dāng)且僅當(dāng)其表示矩陣H相似于如下的Jordan標(biāo)準(zhǔn)型

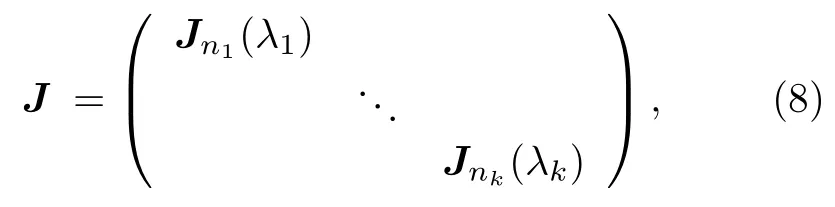
其中 λ1,···,λk為H的全部k個互不相同的實特征根, Jni(λi)(i=1,2,···,k) 為標(biāo)準(zhǔn)Jordan塊.

推論2設(shè) H 是 K 上的線性算子且為共軛線性對稱的, 若 H 有n個互不相同的實特征值, 則H為完整共軛線性對稱.

4 線性算子的PT?對稱性以及完整PT?對稱性

本節(jié)討論 PT ?對稱線性算子的一般性質(zhì).為此, 我們回顧文獻(xiàn)[27]中關(guān)于 PT ?框架的概念.

定義 4[27]設(shè) H 是 K 上的線性算子, P ,T 是K上的算子, 且滿足以下條件：

(2) P2=T2=I , PT=TP , 則稱 { P,T} 是K上的 PT ?框架.

若 { P,T} 是 K 上的 PT ?框架, 且 [ H ,PT]=0 ,則稱算子 H 為 PT ?對稱.

由定義 4 可知, 當(dāng) { P,T} 為空間 K 上的 PT ?框架時, 算子 PT 為 K 上的可逆共軛線性算子.于是, 當(dāng) H 為 PT ?對稱算子時, 它必然是 PT ?對稱的(定義2), 從而是共軛線性對稱的算子.

反之, 若 H 為共軛線性對稱的, 所以定理2 (v)成立, 即存在共軛線性算子 T 滿足 T2=I ( K 上的恒等算子), 且 [ T ,H]=0 .記 P =I , 則 { P,T} 為是K 上的 PT ?框架且 H 為 PT ?對稱.

以上討論說明了共軛線性對稱性和 PT ?對稱性的有以下關(guān)系.

命題2空間 K 上的線性算子 H 為共軛線性對稱算子當(dāng)且僅當(dāng)存在 K 上的某個 PT ?框架{P,T}使得 H 為 PT ?對稱.

設(shè) P ,T 和 H 分別是 P ,T 和 H 的表示矩陣, 則{P,T}構(gòu)成 PT ?框架等價于以下矩陣等式成立：

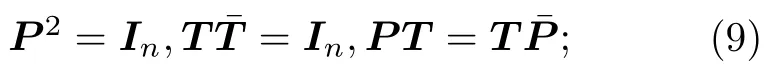
H 為 PT ?對稱等價于以下矩陣等式成立：

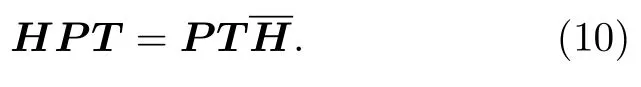
由定理1, 易得到下面的命題.

命題 3設(shè) { P,T} 是 K 上的 PT ?框架, 則σ(PT)要么為空集, 要么為復(fù)平面上的單位圓周.

命題 4設(shè) { P,T} 是 K 上的 PT ?框架, 其中T定義為

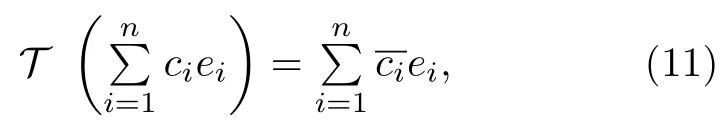
且 H 是 K 上的線性算子, 則

(i) { P?,T} 為 K 上的 P?T ?框架;

(ii) H 為 PT ?對 稱 的 當(dāng) 且 僅 當(dāng) H?為 P?T ?對稱的.

證明(i) 由(11)式知, T 的矩陣表示為單位陣 In, 且 T=In.由于 { P,T} 構(gòu)成 K 上的 PT ?框架, 所以(9) 式成立.從而,

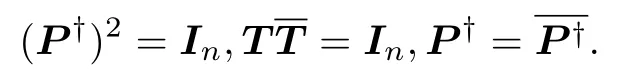
因此, { P?,T} 也構(gòu)成 K 上的 P?T 框架.

(ii) 因為

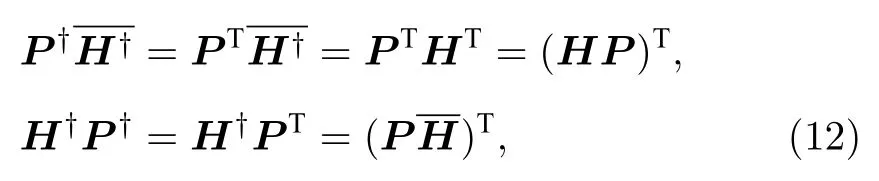
類似于完整共軛線性對稱, 可以給出完整 PT ?對稱定義.

定義 5[27]設(shè) H 是 K 上的線性算子, { P,T} 是K 上的 PT ?框架, 若 H 是 PT ?對稱的且它的特征態(tài)都是 PT 的特征態(tài), 則稱 H 是完整 PT ?對稱.

由定理3及推論2容易得到下面的定理.

定理 4設(shè) { P,T} 是 K 上的 PT ?框架, H 是K上的線性算子且為 PT ?對稱的, 則

(a) H 為完整 PT ?對稱的當(dāng)且僅當(dāng) H 的譜為實的, 且 H 為非簡并的;

(b) H 為完整 PT ?對稱的且可相似對角化當(dāng)且僅當(dāng) H 有n個互不相同的實特征值.

例 2設(shè) { P,T} 是 2 維復(fù)空間 K 上的 PT ?框架 , H1為 K 上 的 線 性 算 子, P ,T,H1的 表 示 矩 陣P,T,H1為

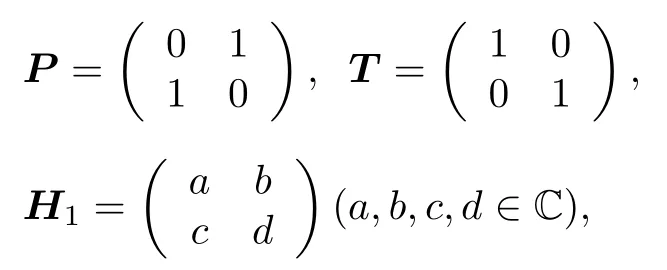
則 H1為 完 整 PT ?對 稱 的 當(dāng) 且 僅 當(dāng)|b|2≥(Ima)2且 b0 .

證明充分性.設(shè)|b|2≥(Ima)2且 b0 .

計 算 可 知 ：H1的 兩 個 特 征 值 λ=Rea±當(dāng) | b |2-(Ima)2≥0 , H1特征值均為實數(shù).下面分兩種情況進(jìn)行討論.

(1) 當(dāng) | b |2-(Ima)2＞0 時, H1有 兩 個 不 相 同的實特征值.進(jìn)而, 由定理4(b)知 H1為完整 PT ?對稱的.

(2) 當(dāng) | b |2=(Ima)2時, σ (H1)={λ} , 且實特征值 λ =Rea 的代數(shù)重數(shù)為2.由于

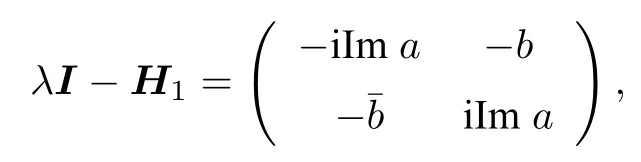
必要性.設(shè) H 為完整 PT ?對稱的, 則 H 為 PT ?對稱, 且由定理4(a) 知：H的特征值均為實的且 幾 何 重 數(shù) 為 1.因 為 H1為 PT ?對 稱 的 , 所 以于是, 由充分性的證明可知：H1的兩個特征值為由于H的特征值均為實的, 所以 | b |2-(Ima)2≥0 .假若b=0, 則 I ma=0 , 從 而 λ I-H1為 零 矩 陣 , 即H1=λI .這與 H1的特征值 λ =Rea 幾何重數(shù)為1矛盾.故 b0 .證畢.

例 3設(shè) { P,T} 是 2 維 復(fù) 空 間 K 上 的 PT 框架 , H2為 K 上 的 線 性 算 子 , P ,T,H2的 表 示 矩 陣P,T,H2為

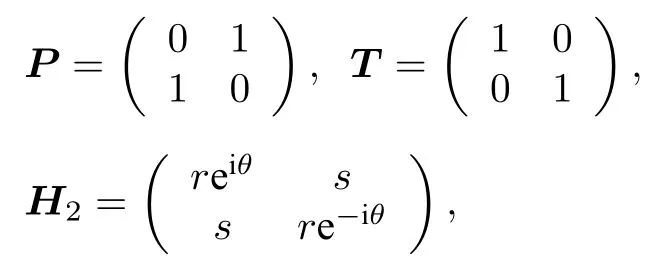
其中 r ,s,θ 是非零實數(shù), 則由例2知, H2為完整PT ?對稱的當(dāng)且僅當(dāng) | s |≥ |r·sinθ| .

例 4設(shè) { P,T} 是 3 維復(fù)空間 K 上的 PT 框架,H3為 K 上的線性算子, P ,T,H3的表示矩陣P T,H3為

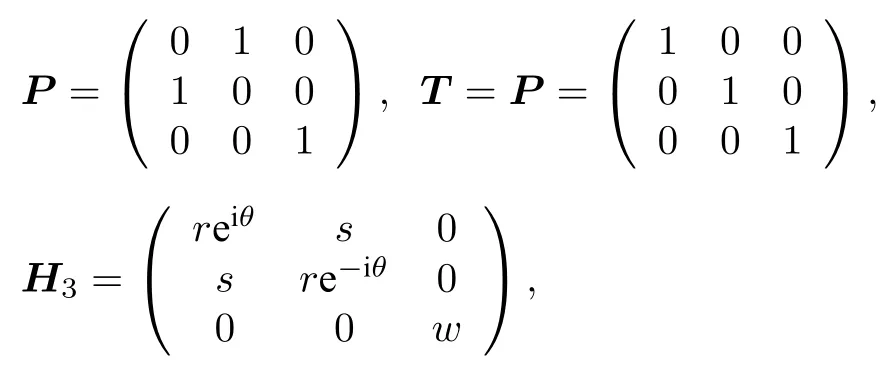
設(shè) { Pk,Tk} 是 復(fù) 空 間 Kk上 的 PkTk?框 架 (k =1, 2) , 定義張量積空間 K1?K2上的算子如下：

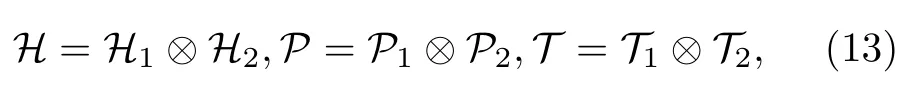
其中, 線性算子 A1與 A2的張量積 A1?A2的定義與通常相同, 即

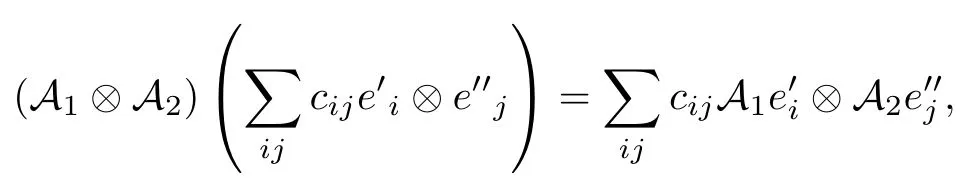
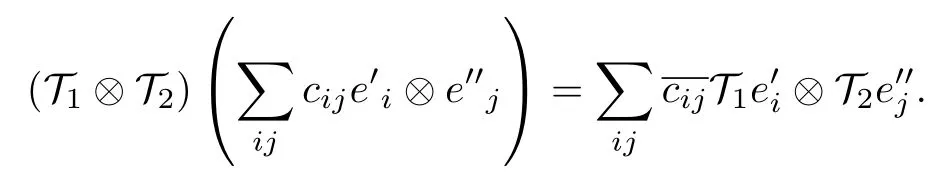
易知, { P,T} 是空間 K1?K2上的 PT ?框架且 H 是PT ?對稱的 (參見例 5).這就說明：PT ?框架及PT?對稱性對張量積運算“具有封閉性”.

例 5設(shè) { Pk,Tk} 是 2 維復(fù)空間 K 上的 PkTk?框架 ( k=1,2) , Hk為 K 上的線性算子(k=1,2),Pk,Tk,Hk的表示矩陣 Pk,Tk,Hk為

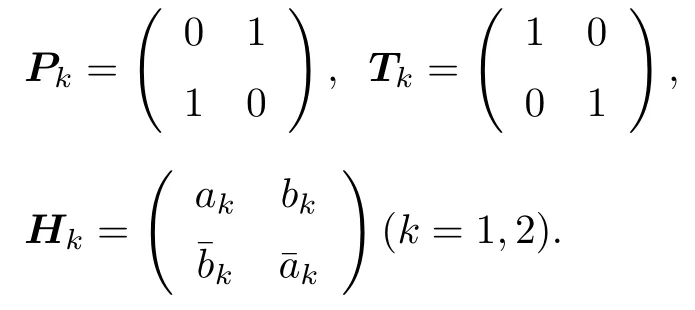
顯然, Hk為 PkTk?對稱的 ( k=1,2) , 從而,H1?H2為 PT ?對稱的, 其中P=P1?P2,T=T1?T2.

但是, 完整 PT ?對稱性對于張量積運算“不具有封閉性”, 即 Hk是完整 PkTk?對稱的 ( k=1,2) 不能保證張量積 H1?H2一定是完整 PT ?對稱的, 其中 P =P1?P2,T=T1?T2(例6).

例 6設(shè) { Pk,Tk}(k=1,2) 是 2 維復(fù)空間 K 上的 PkTk框 架 , Hi為 K 上 的 線 性 算 子 ,Pk,Tk,Hk的表示矩陣 Pk,Tk,Hk分別為

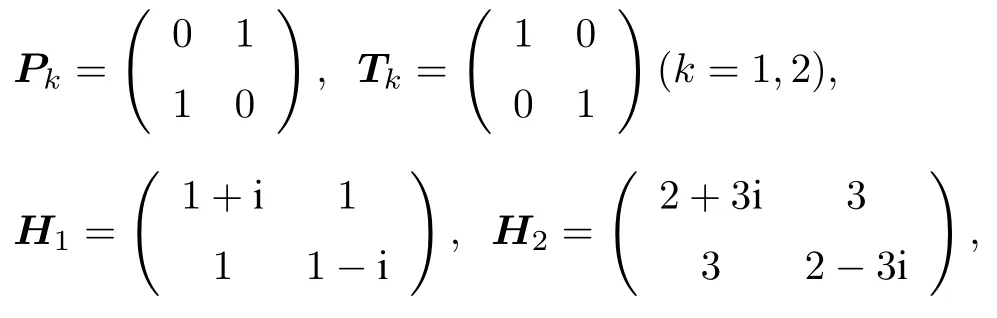
容易看出, H1的特征值為1, 代數(shù)重數(shù)為2, 幾何重數(shù)為1, H2的特征值為2, 代數(shù)重數(shù)為2, 幾何重數(shù)為1.由定理4知, Hk(k=1,2) 都是完整PkTk(k=1,2)?對 稱 的 .因 此 , H =H1?H2為 PT ?對稱的, 其中 P =P1?P2,T=T1?T2.下面說明H不是完整 PT ?對稱的.

計算可知

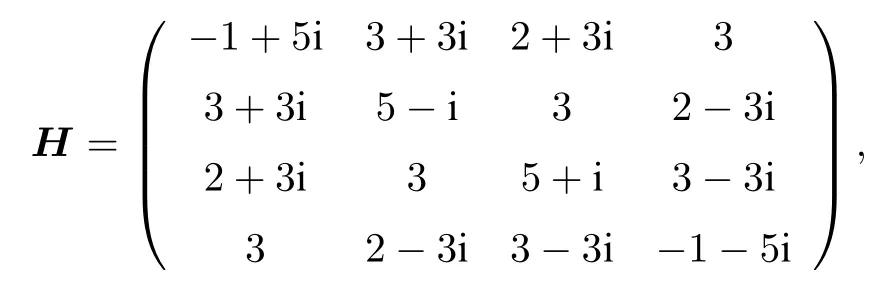
它只有一個特征值2, 其代數(shù)重數(shù)為4、幾何重數(shù)為 2.從而由定理 4(a) 知：H 不是完整 PT ?對稱的.

下面從矩陣分析的角度來考查例6的更一般的情形.

設(shè) Hk(k=1,2) 為2維空間 K 上線性算子且是完整 PkTk?對稱的 ( k=1,2) , Pk,Hk分別為Pk,Hk的表示矩陣, 且

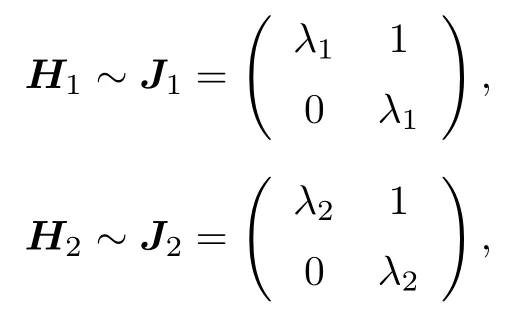
即存在可逆矩陣 Qk(k=1,2) 使得Hk=QkJk×(k=1,2), 從而H1?H2=(Q1?Q2)(J1?J2)(Q1?Q2)-1.

設(shè) H ,P,T 按照 (13)式定義, H ,P,T 為對應(yīng)的表示矩陣.下面說明 H 不是完整 PT ?對稱的.

又因為H=H1?H2～J1?J2, 所以

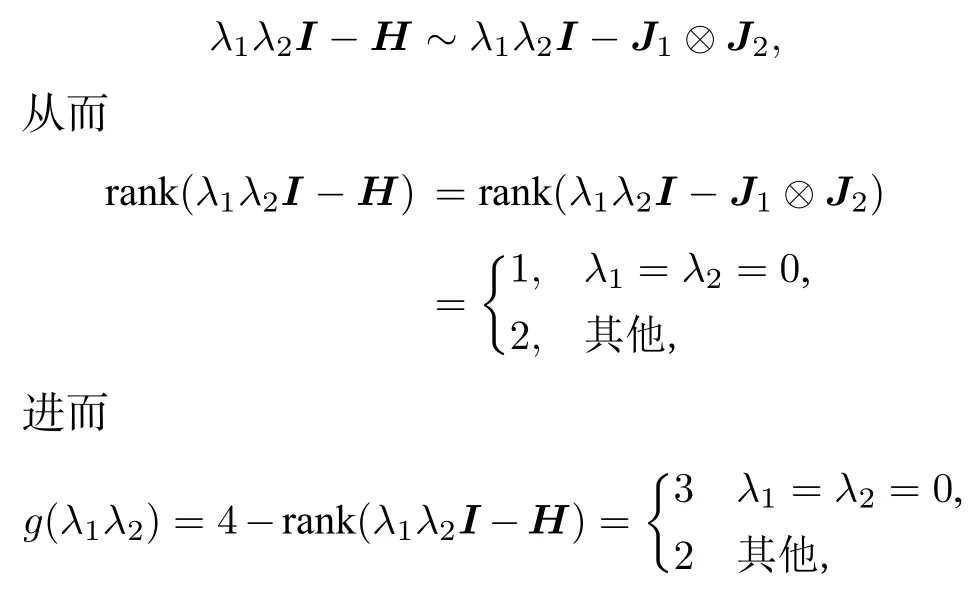
其中 g (λ1λ2) 為 λ1λ2的幾何重數(shù).由定理4(a)可知：H 不是完整 PT ?對稱.

下面簡單說明 PT ?對稱量子系統(tǒng)與經(jīng)典量子系統(tǒng)之間的轉(zhuǎn)化關(guān)系.設(shè) { P,T} 是 K 上的 PT ?框架, H 為哈密頓且為 PT ?對稱的.PT ?對稱量子理論的關(guān)鍵在于構(gòu)造一個線性算子 C , 建立一個新的正定內(nèi)積, 稱之為 C PT ?內(nèi)積, 使得 H 關(guān)于 C PT ?內(nèi)積為自伴的, 從而保證系統(tǒng)的演化關(guān)于新內(nèi)積為酉演化且概率守恒.因此, 問題的本質(zhì)在于尋找一個新的正定內(nèi)積, 使得系統(tǒng)哈密頓 H 在這個內(nèi)積下是自伴的.

給定空間 K 上的正定算子 η , 可以定義 K 上的新內(nèi)積稱之為 K 上的 η ?內(nèi)積.我們在文獻(xiàn)[37]中給出了線性算子關(guān)于某個正定內(nèi)積是自伴的一些等價條件, 證明了存在正定算子η使得 H 關(guān)于 η ?內(nèi)積是 K 上的自伴線性算子當(dāng)且僅當(dāng) H 的表示矩陣H相似于一個實對角陣.哈密頓H 的完整 PT ?對稱性保證了 H 的特征值是實數(shù), 但并不能保證其表示矩陣H可相似對角化.由命題5知：H 為完整 PT ?對稱的且可相似對角化當(dāng)且僅當(dāng) H 有n個互不相同的實特征值.因此, H 的完整PT ?對稱性不是 H 關(guān)于某個新的正定內(nèi)積下自伴的充分條件, 同時也不是必要條件.

5 結(jié) 論

本文討論了共軛線性算子的一些性質(zhì), 給出了共軛線性對稱和完整共軛線性對稱的定義, 給出了共軛線性對稱性和完整共軛線性對稱性的等價刻畫; 在此基礎(chǔ)上, 進(jìn)一步討論了 PT ?對稱及完整PT ?對稱的性質(zhì), 給出了完整 PT ?對稱哈密頓的一些具體例子, 說明了完整 PT ?對稱性對張量積運算不具有封閉性, 同時還說明了完整 PT ?對稱性既不是哈密頓 H 在某個正定內(nèi)積下自伴的充分條件, 也不是必要條件.通過本文的討論, 可以幫助我們更好地理解共軛線性對稱性的本質(zhì), 使我們對 PT ?對稱量子系統(tǒng)相應(yīng)的數(shù)學(xué)結(jié)構(gòu)有更清楚的認(rèn)識, 對將來的進(jìn)一步研究具有一定的理論意義.