Review of Antiswing Control of Shipboard Cranes
Yuchi Cao and Tieshan Li
Abstract— Shipboard cranes are extensively utilized in numerous fields such as cargo transferring and offshore engineering.The control of shipboard cranes, especially the antiswing control of payloads, has attracted much research attention due to their typical underactuation characteristics and complicated dynamics.Through comparisons of the traditional land-fixed cranes, a brief review on modeling and dynamics analysis is presented to illustrate the tremendous challenges and difficulties in controller design for shipboard cranes. A comprehensive review and brief analysis of shipboard crane control strategies are further presented. Some future research directions are also put forward for reference. It is expected that the paper will be useful for improving existing control schemes and generating novel control approaches for shipboard crane systems.
I. Introduction
WITH the rapid growth of the global economy and the rising demands on marine resource exploration, shipboard cranes have become extensively utilized to carry out complicated tasks such as cargo transferring, wreck salvaging,installation and maintenance of offshore constructions, and so on. For example, cargo transferring operations between two ships are carried out more frequently in open sea due to the increased ship draft and limited depth available in fairways and harbors.
Cranes are a typical class of underactuated systems with less control inputs than their degrees of freedom (DOFs), and are also sophisticated multi-input and multi-output (MIMO)nonlinear systems with complicated dynamics and strong coupling characteristics. The payload will swing inevitably due to actuator movements and the inertia during boom/jib movements and/or hoisting/lowering payloads. Moreover,shipboard cranes are fixed on ship decks so they work in noninertial coordinate frames, which is substantially different with land-fixed cranes. In addition, unpredictable ship motion caused by wave fluctuations, currents, and winds may amplify the payload swing amplitudes and render more difficulties in precise payload positioning. A poor or failed antiswing control on payload may pose great dangers or damages to the payload and other objects around the operating environment[1]. More DOFs are involved in shipboard cranes than that of land-fixed cranes, which leads to the dynamic models of shipboard cranes being much more complicated. Based on the above adverse factors, existing control methods designed for land-fixed cranes [2]–[12] cannot be applied to shipboard cranes directly, which brings extra challenges and difficulties for the controller design of shipboard cranes.
Effective antiswing controls for shipboard cranes not only contribute to the control theory and application, but also prompt the development and efficiency of marine industry.However, research in antiswing control of shipboard cranes is still in their initial phases, and there are still many issues to be resolved in the future. Motivated by these considerations, this manuscript aims at summarizing existing literature and analyzing their relative merits. Therefore, some innovative ideas may be inspired to improve the effectiveness of antiswing control of shipboard cranes.
The remaining parts of the paper are organized as follows:modeling and dynamics analysis of various types of shipboard cranes are briefly introduced in Section II to illustrate their typical characteristics and challenges in controllers design. In Section III, some dominating control strategies on antiswing of payloads are clarified out into categories and briefly commented. Some future research directions are put forward for reference in Section IV. Conclusions are finally given in Section V.
II. Mathematical Models of Shipboard Cranes
Based upon the primary dynamic properties and DOFs at the suspension cable connection point, shipboard cranes can be roughly categorized into three types: shipboard overhead cranes, shipboard boom cranes, and shipboard tower cranes.The payload is supported by a suspension cable. Shipboard overhead cranes are usually used to load or discharge containers, so it is sometimes called a shipboard container crane. The trolley moves along a bridge and the movement direction of the bridge is perpendicular to that of the trolley to convey containers to a desired position. For shipboard boom cranes, a boom can rotate both perpendicular and parallel to the ship deck. For shipboard tower cranes, the horizontal jib arm can rotate around a vertical tower, and the trolley moves along the jib arm in the radial direction [13].
Compared with land-fixed cranes, dynamic models of shipboard cranes are much more complicated due to the existence of complex external disturbances. Generally, if the shipboard crane is considered as single-pendulum model, then it has 11 DOFs in total [14]. The number of DOFs greatly increases for shipboard cranes governed by a double-pendulum model. Taking a shipboard boom crane as a singlependulum model as an example, the crane has 5 DOFs, as shown in Fig.1, and the ship has 6 DOFs, the surge, sway,heave, roll, pitch and yaw. Related parameters applied in shipboard crane model are listed in Table I. It is much more complex and challenging to design an effective controller for the full system, and it is sensible and acceptable to focus on the primary DOFs while ignoring the less important ones according to specific operation conditions.
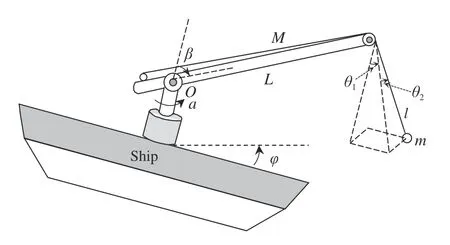
Fig. 1. 5 DOFs of shipboard boom crane: the boom’s slew angle and luff angle payload radial swing angle and tangential swing angle and suspension cable length (l).
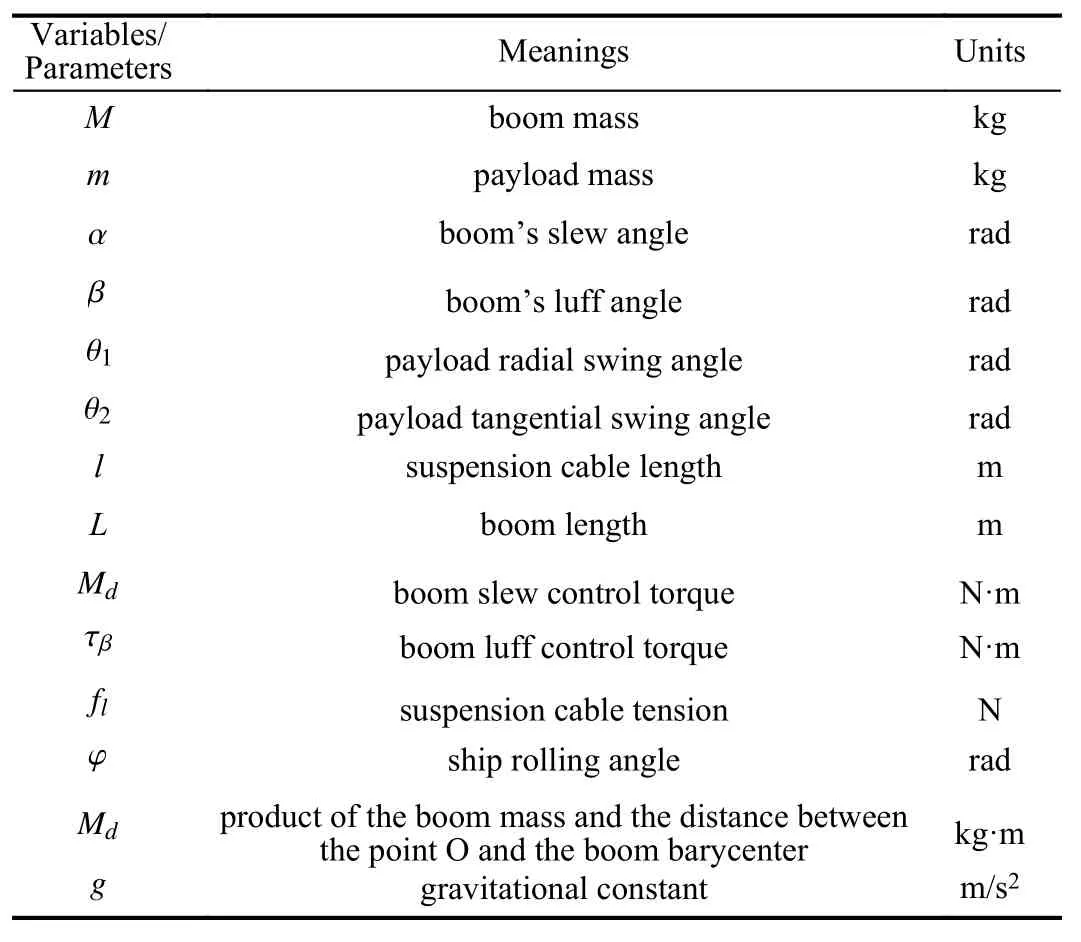
TABLE I Parameters of Shipboard Crane Model
Throughout the past decades, much research with regards to modeling and dynamics analysis of shipboard cranes have been conducted. In [15], a kinematic model of payload was established based on Lagrange equations while considering ship roll and pitch. The influencing factors of payload swing were further analyzed via numerical simulation under the conditions of different suspension cable lengths, different excitation frequencies, and different hoisting/lowering speeds,respectively.
In [16], considering the boom luff and slew angles,suspension cable reeling, and unreeling operation, a 8-DOF nonlinear crane-ship dynamic model was developed, which incorporated 6 DOFs of ship motion and payload radial and tangential swing angles of boom crane. Coupled effects between ships and cranes were analyzed via simulation in regular and irregular starboard waves, respectively. By employing the Lagrange equations, the relative kinetic energy was depicted in the non-inertial coordination frame established on the ship, and then the dynamic model of the shipboard boom cranes were obtained in [17], which also took the 6 DOFs of ship motions in to consideration. In [18],during the ship-to-ship cargo transfer operation, the mother ship was assumed to be stationary, and the heave, roll, and yaw of the barge fixed with crane were taken into consideration, resulting in a 5-DOF shipboard boom crane model being developed as follows:
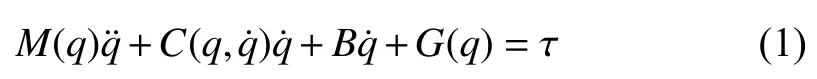

Due to the complexity of dynamic models and the difficulties in controller design, most existing research focuses on 2-DOF or 3-DOF shipboard crane systems. Lagrange’s method was employed by [14] and [19] to set up 3-DOF dynamic model for shipboard boom cranes (boom’s luff angle,payload radial swing angles, and suspension cable length) in the presence of ship roll and/or heave in following forms:
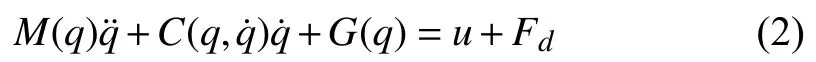
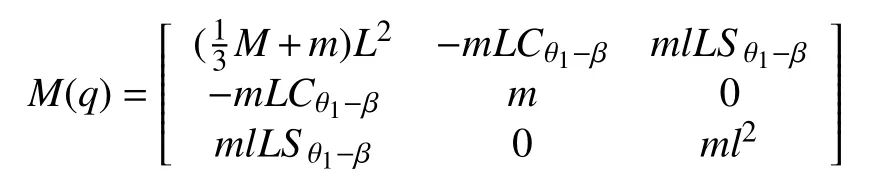

Considering the ship motions (sway, heave, and roll) and frictions existing in the system simultaneously, a 3-DOF dynamic model (trolley position, suspension cable length, and payload radial swing angle) was developed for the shipboard tower crane in [20]. A 4-DOF shipboard tower crane model(slew angle, trolley position, payload radial angle, and tangential swing angle) was presented in [21] while considering the roll and heave of the ship.
Considering the roll and heave of the ship relative to the inertial reference frame, a 3-DOF dynamic model (trolley position, suspension cable length, and payload radial swing angle) of a shipboard container crane was proposed in [22].The ship’s heaving, pitching, and rolling motions were considered in sea state 3, and then a dynamic model of container crane on a mobile harbor was derived by using the Lagrange method and simulations carried out in [23].Furthermore, [24] took the wind-induced disturbance on the payload into consideration. In [25] and [26], a new mathematical model of shipboard container cranes were constructed by regarding the ship as a rigid body suspended on a damper-spring foundation with viscoelastic seawater.Moreover, the flexibility of the suspension cable was also taken into consideration. Six fully nonlinear equations of motion were obtained finally to reflect the relationships among two inputs (pulling force of the trolley and torque of the hoist) and six outputs (trolley displacement, suspension cable length, axial container oscillation, container swing angle, ship roll, and heave).
Most existing dynamic models for various types of shipboard cranes were established based on Lagrange’s equations. To facilitate the controller design, the number of DOFs might be decreased, or the model was further linearized according to a specific point of view. Most dynamic models ignored the frictions or the flexibility of the suspension cable,so they may not depict the dynamic characteristics of the shipboard cranes in an accurate and full-scale manner.
III. Antiswing Control of Shipboard Cranes
The main control objectives of shipboard cranes are to convey the payload to a designated position accurately and quickly in safe manner, and to suppress the payload swing rapidly. Moreover, some research also takes physical limitations and constraints into consideration, such as input saturation, limitations on suspension cable length, and the flexibility of the suspended cable.
Underactuation characteristics of shipboard crane systems impose great difficulties on controller design, so some researchers resort to mechanisms of eliminating payload swing. For example, the rider block tagline system (RBTS)was proposed in [27] and [28]. The swing angle of the payload can be reduced by changing the frequency of the pendulum by using a tagline and a rider block. Maryland Rigging was proposed and applied in [29]–[34]. A pulley was attached on the cable which was connected to two different points of the boom, and the suspension cable was then connected to the pulley. The pendulation of payload could be significantly reduced by actively changing the length of the pulley cable and controlling the motion of the pulley. In [35] and [36], an active anti-pendulation arm was designed as a partial structure of the shipboard boom cranes. One end of the anti-pendulation arm was attached on the boom-tip, and the other end of the control arm was attached on the suspension cable. The arm could be actuated to dampen the pendulations of the payload.A sling tray mechanical anti-swing system (STMAS) was proposed in [37]–[40], which reduced the length of the suspension cable to effectively decrease the swing amplitude of the payload. In [41], the shipboard boom crane was installed on an anti-swing platform. Two hydraulic cylinders were fixed between the upper plate and lower plate in bow/stern direction to compensate the ship’s pitching motion,the other two in port/starboard direction to compensate the ship’s rolling motion. To ease the load of the aforementioned four cylinders, a main support shaft was mounted.
In practice, it may be difficult to maintain the mechanisms in good conditions due to their complicated structures.Mechanisms are also employed to deal with the payload residual swing passively without theoretical guarantee.Moreover, additional control methods may be also needed to promote the effectiveness of the mechanisms. Due to defects mentioned above, some researchers begin to resort to only meaningful controller design to obtain satisfactory performance. The mainstream control approaches on antiswing control of shipboard cranes, as shown in Fig. 2, are briefly listed and analyzed in groups.
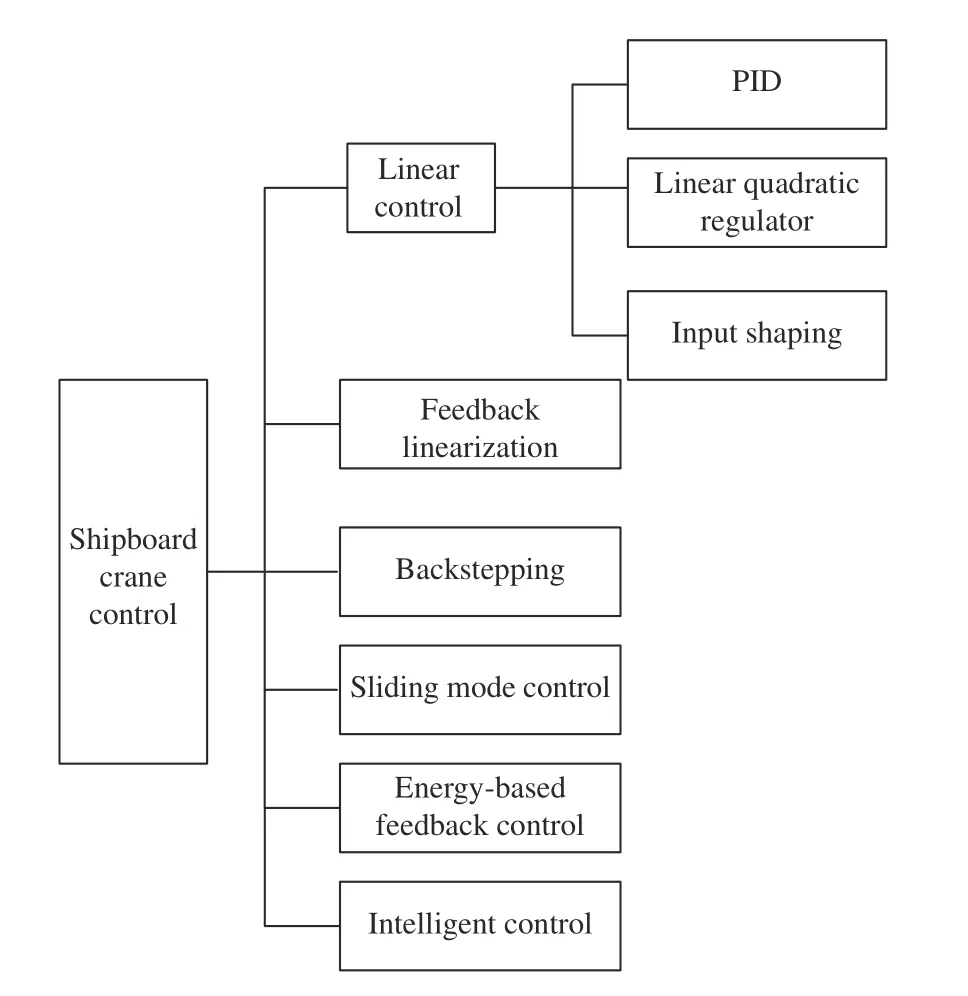
Fig. 2. Control schemes for shipboard cranes.
In order to simplify the dynamic model establishment and facilitate the controller design, some assumptions are commonly taken in existing literature, such as:
Assumption 1:The payload is always beneath the boom/jib top, which means
Assumption 2:The payload is considered as a point mass.
Assumption 3:The suspension cable is massless, and it is always straight due to persistent strain.
Moreover, friction in the shipboard cranes may also be ignored in some dynamic models.
A. Linear Control
Due to the convenience and simplicity of linear control strategies, some research focuses on controller design based on linearized shipboard crane dynamic models.
1) PID:Proportional integral derivative (PID) control is pervasively applied to cranes [42]. Most PID controllers were developed in combination with other control techniques[43]–[48]. After the identification of a virtual plant built in the Computation Fluid Dynamic Software FLOW-3D, an integrated control model including ship and crane was finally obtained. An optimal method comprised of PI controllers, a low pass filter, and a notch filter was proposed in [49] to reduce the payload residual swing. In [50], a PID expert controller was designed. The payload pendulation could be decreased by 3 degrees according to the numerical simulation results. In [51], an adaptive sliding mode PID controller was developed for the 2-DOF mobile harbor container crane, and the controller was verified by virtual mechanical model created by SOLIDWORKS and exported to the automatic dynamic analysis of mechanical system (ADAMS). Compared with traditional build-and-tests, virtual simulation can improve the quality of products and reduce costs and errors. In[52], a neural network PID control scheme was proposed for shipboard special boom cranes. The PID parameters can be tuned by back propagation neural networks (BP NNs).Simulation results demonstrated that satisfactory performance could be achieved even in the presence of ship roll.
2) Linear Quadratic Regulator:In [53], a micro-trolley with an additional two DOFs was installed inside the conventional macro-trolley to compensate for its position and suppress the payload swing. A linear quadratic regulator (LQR) anti-swing controller was further designed based on the linearized shipboard container crane model. In [30], a linearized dynamical model of shipboard crane with Maryland Rigging was obtained based on Lagrange’s equations; a LQR controller was further designed to reduce the pendulation of the payload.
3) Input Shaping:Based on the natural frequencies and damping ratios of the system, the input signal is convolved with a sequence of impulses of varying amplitudes and time delays, so that the system’s vibration can be reduced or eliminated. By integrating input shaping technology and close-loop feedback control, an anti-swing control scheme was proposed in [54], with simulation results demonstrating that the payload swing angle could be significantly decreased.
Under the assumption that all state variables were near the equilibrium point, the linear control methods mentioned above were further derived on the basis of linearizing the complicated nonlinear dynamic models of shipboard cranes.Due to the persistent and unexpected disturbances induced by waves and winds, the payload may swing with large amplitudes. So, it is unrealistic that the state variables are always close enough to the equilibrium point, and thus the control performance may be significantly degraded.Furthermore, the robustness of the linear or simplified model is not enough for the system uncertainties, such as payload masses and friction coefficients.
B. Feedback Linearization
The Pierson-Moskowitz energy density spectrum was employed to describe disturbances induced by waves.Nonlinear stochastic differential equations were used to describe the dynamic model of two dimensional shipboard cranes, and a controller based on feedback linearization was proposed in [55]. A nonlinear controller for 3-DOF shipboard boom crane was designed in [56] by integrating learning strategies with partial feedback linearization methods. The learning strategy is used to deal with the periodic disturbance with unknown boundaries. An adaptive repetitive learning control strategy was proposed for 3-DOF shipboard boom cranes in [57], which could handle system parameter uncertainties. A period identifier was further introduced to address unknown periods of the periodical disturbances. The stability was guaranteed based on Lyapunov theory.
Based on the mathematical model of shipboard container crane constructed in [25] and [26], the whole system was further decomposed into actuated and underactuated subsystems, and a nonlinear feedback controller was proposed in [25]. In [58], the Bouc-Wen model was employed to describe the output hysteresis mechanism existing in shipboard container crane. The Luenberger-type observer was designed to estimate the velocity variables. A controller was developed based on the combination of feedback linearization techniques and PD action.
Due to the inherent principles of feedback linearization techniques, some useful nonlinear terms may be cancelled, so coupled nonlinear characteristics of the shipboard cranes may be not utilized fully and effectively.
C. Backstepping
Backstepping technologies provide a recursive and systematic way to construct Lyapunov functions for strict feedback systems [59], [60]. A control approach based on a backstepping technology was presented in [61] for shipboard special boom cranes, which could drive joints of crane booms to track the trajectory smoothly and suppress the swing effectively.
Although backstepping techniques are an effective control scheme for strict feedback systems, their application is badly impeded due to difficulties in transforming the shipboard crane system models into strict feedback forms.
D. Sliding Mode Control
Sliding mode control (SMC) has been widely applied in diverse fields, including crane control [62]–[65]. The SMC is effective and suitable for conditions with system uncertainties and external disturbances due to its strong robustness. The main drawback of SMC is the chattering problem [66], [67].SMC is employed by many studies to deal with parameter uncertainties and wave-induced disturbances contained in shipboard cranes.
In [68], a new mechanism attached to the trolley was designed to suppress the payload tangential swing induced by the pitching motion of ships. An SMC controller was further designed for the shipboard container crane during the ship-toship cargo transferring operation while considering the ship’s roll and heave motion. Compared with the PD controller, a better performance could be achieved. Due to the ship rolling motion, the residual radial swing might exist even when the trolley reached its desired position, so it may continue to move around the desired position to suppress the residual radial swing of the payload. After considering different motions of the ship, models of stationary shipboard boom cranes and payload sway were presented in [69]. An active sway damping SMC approach was further developed and several simulation results were illustrated to verify the effectiveness of the proposed controller. A second-order SMC was designed in [14] for shipboard boom crane to track the trajectory and suppress the payload swing. Actuator chattering was alleviated while achieving satisfactory control performance and preserving its strong robustness. Considering the roll and heave motion of ship, a hierarchical SMC was developed in [70] for shipboard container cranes, which was further verified by virtual prototype and hardware platform. In[71], a robust dual stage trolley control scheme based on SMC was proposed for the 4-DOF container crane.
Apart from the direct application of SMC as mentioned in[68] and [69], SMCs may integrate other control approaches for shipboard cranes. Considering the roll and heave motion of the ship, and wind-induced disturbance, a sliding surface was designed using the LQR design approach in [24] for a linearized 3-DOF shipboard container crane model to handle uncertainties and bounded disturbances. The robust SMC could implement the operations of hoisting, moving, and lowering containers in the presence of ocean waves and short burst/persistent wind disturbances. Considering the roll motion of ship, a sliding surface with the flexible parameter was established in [72] for a linearized 3-DOF shipboard container crane. The flexible parameters were tuned by a fuzzy real time inference to adjust the position and antiswing subsystems. Furthermore, a saturation function was introduced into the control law to avoid the chattering phenomenon.Considering the roll and heave motions of the ship and windinduced disturbances, an adaptive neural network secondorder SMC was proposed for shipboard container cranes in[73]. A radial basis function neural network (RBF-NN) was employed to approximate uncertainties in the shipboard container system. Its effectiveness and strong robustness were verified in several operation scenarios with widely varying system parameters and uncertainties. Furthermore, the influence of input backlash nonlinearity was also taken into consideration. Based on the mathematical model of shipboard container cranes constructed in [26], the system was further broken down into actuated and underactuated subsystems, and two robust controllers based on conventional SMC approach and backstepping SMC technology were proposed and compared via numerical simulations. Better performance could be achieved by the backstepping SMC controller. A controller was designed in [58] using the SMC and PD action while considering the output hysteresis.
It can be concluded from the above discussions that SMC was mainly applied in shipboard container cranes, except for the instances in [14] and [26]. The validation of SMC for other types of shipboard cranes can be further explored. Due to its strong ability in dealing with uncertainties, SMC is an effective control approach and a proper tool for shipboard cranes suffering from persistent wave-induced disturbance and parameter uncertainties.
E. Energy-based Feedback Control
Lyapunov’s direct method provides a powerful way to assess system stability. However, it is critical that the appropriate Lyapunov candidate function is chosen. Since physical characteristic of the shipboard crane system is intuitive, some works [11], [74]–[78] constructed the Lyapunov candidate function based on the system mechanical energy, and then derived the final feedback control scheme.Such a controller was derived in [74] for a 2-DOF shipboard tower crane in the presence of ship roll. Without linearizations for 3-DOF shipboard tower crane model, an adaptive robust tracking controller was designed in [20]. An adaptive law was introduced to handle system uncertainties such as trolley mass, payload mass, and friction coefficients. A robust term was included to deal with unknowns and bounded disturbances, especially for the unmatched disturbances.
Most exiting control methods regarded the motion of ships as disturbances, which makes controller design and stability analysis rather difficult. References [11], [19], [75]–[78]presented a novel way by coordinate transformation operations, so that the roll and/or heave motion of ships were integrated into new state variables and the reference signals of new state variables were transformed into constants, while the reference signals for original dynamic model were time varying including the motions of ship, making it much easier and more convenient for further controller design and stability analysis. In [19], considering roll and heave motion of ships, a nonlinear stabilizing controller was first proposed for a 3-DOF shipboard boom crane, and a better tracking performance was achieved compared with the PD controller, SMC controller designed in [68] and composite controller proposed in [14]. In[75], considering ship roll, a full state feedback controller and an output feedback controller were designed separately for the 3-DOF shipboard boom crane. In [76], an observer-based dynamic feedback controller was designed for 3-DOF shipboard boom cranes while considering ship roll and input saturation simultaneously. The observer could recover the state variables to lower the cost for velocity sensors and to overcome the problem of extra noises caused by traditional numerical differentiation operations. Compared with controllers proposed in [14] and [75], better performance was obtained. Asymptotic stability was proved based on Lyapunov’s theory and LaSalle’s invariance theorem. In [77],a novel model-parameter-free control scheme was proposed for 3-DOF shipboard boom cranes while considering ship roll motion, so the proposed controller could perform satisfactorily whether the exact system parameters, such as payload/jib masses, were known or not. Thus, system robustness was greatly enhanced. Moreover, a barrier function was introduced to restrict the cable length within the permitted range. Control methods mentioned above provide a novel way for designing 3-DOF shipboard boom cranes, which may be further applied to other types of shipboard cranes. In [78], a nonlinear coordination controller was established for 3-DOF shipboard boom crane suffering from ship roll and heave motion. A disturbance observer was designed to tackle external disturbances and unmodeled dynamics. Actuator saturation could be satisfied by tuning the control parameters properly.Moreover, two actuators could be well coordinated to enhance the efficiency.
These aforementioned shipboard cranes are regarded as single-pendulum models, which means that the hook mass and the distance between the hook and payload are completely ignored. In many practical situations, the center of gravity of the payload and hook do not coincide with each other due to the non-negligible hook mass and large-scale payload,shipboard cranes are operated in complex double-pendulum model [11], [79], [80]. The double-pendulum phenomenon makes the controller design more complicated and challenging by introducing additional DOFs to be controlled while the number of actuators remains the same. To deal with these problems, a 4-DOF dynamic model of double-pendulum shipboard boom cranes (jib luffing angle, suspension cable length, hook swing angle, and payload swing angle) were established in [81] while considering ship roll. A coupling nonlinear feedback controller was then elaborately designed,and the suspension cable length was limited within a preset range. The asymptotic stability was finally proven based on theoretical analysis without any linearization or approximation operations.
The energy-based feedback control provides an effective and intuitive way to construct the Lyapunov candidate function based on the system mechanical energy. Coordinate transformation can be further employed to integrate the ship motion into new state variables, hence, the control objective is simplified and the controller is easier to be designed. It is a suitable and effective control approach for shipboard crane control.
F. Intelligent Control
Intelligent control has been utilized in extensive fields,especially those with complicated systems which are difficult to be solved by traditional control approaches. Due to their strong nonlinearity, system uncertainties, and complicated control objectives, some intelligent control methods have been applied in shipboard crane systems. In [11], based on the nonlinear equations of a shipboard crane with Maryland Rigging, a fuzzy controller was developed in which the change in the length of the suspension cable was the control action. In [82], considering the ship rolling motion in sea state 2 or 3, a fuzzy controller was designed for 2-DOF shipboard cranes. In [83], a T-S fuzzy controller was proposed for shipboard container crane. A fuzzy control strategy for an offshore container crane was proposed in [84] with a combination of PD controller and compensation mechanism.In [85], a hierarchical intelligent control scheme was proposed for a shipboard multi-joint foldable boom crane, and the execution of the control system was carried out with a fuzzy neural controller, where the joints could move along the desired trajectory. In [86], a neural network-based adaptive controller was developed for 3-DOF shipboard boom cranes with ship roll motion while considering the input dead zones.
Although intelligent control has been applied in many fields, application in shipboard crane control is still not very common. It is expected that more and more control schemes based on intelligent control are elaborately designed for shipboard crane systems.
IV. Future Research Directions
After comprehensive review and careful analysis for existing control methods, some meaningful and practical results have been obtained for shipboard cranes. Due to the complex nonlinearity, unexpected wave-induced and windinduced disturbances, and system uncertainties, there are still some issues required for further research.
1) System robustness should be enhanced further to handle parameter uncertainties and complicated disturbances, so the shipboard cranes can implement various operation tasks safely and effectively in rough sea conditions.
2) More physical characteristics of shipboard cranes should be taken into consideration simultaneously, such as state constraints, input saturation, and energy savings, so the controller will be more practical.
3) Take the volume of payload and the distance between the hook and payload into consideration. Existing research mainly treat the hook and payload as the same mass points by ignoring the volume of payload and the distance between the hook and the payload, which is similar to the single-pendulum model. In practice, especially for large-scale payloads, the center of gravity of the payload and hook do not coincide, so shipboard cranes often operate in a double-pendulum manner.Thus, the DOFs of the whole system will increase, which significantly increase the complexity of the dynamic model and make its controller design more challenging.
4) Time-varying trajectory tracking controls can be analyzed for shipboard cranes. Most existing controllers are designed for time-invariant desired positions. Moreover,efficiency is also an important criterion that should be considered in controller design for shipboard crane systems,as it would attain better performances to implement the control objectives with less energy consumption in finite time.
5) Comprehensive control research for shipboard cranes can be further expanded into 3 dimensions. Existing works primarily focus on controller design for 2-DOF or 3-DOF shipboard cranes in 2 dimensions. In practice, shipboard cranes must be operated in 4-DOF or 5-DOF mode and 3 dimensions to transfer the payloads to designated positions.
6) Coordinated control of multiple shipboard cranes may be researched to enhance their capability and efficiency. As far as we know, all existing control schemes are designed for single shipboard crane. In practice, two shipboard cranes may be operated together to convey a heavy payload which may be over the limit of safe working loads for each individual crane.
V. Conclusion
This paper has summarized and reviewed most of the existing research on antiswing control approaches for various types of shipboard cranes. As a typically nonlinear and underactuated system applied in cargo transferring and offshore engineering, although shipboard crane control has been studied broadly and some valuable results have been achieved, there are still some open issues requiring further attention.
 IEEE/CAA Journal of Automatica Sinica2020年2期
IEEE/CAA Journal of Automatica Sinica2020年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Artificial Intelligence Applications in the Development of Autonomous Vehicles: A Survey
- Data-Driven Based Fault Prognosis for Industrial Systems: A Concise Overview
- Research Progress of Parallel Control and Management
- Influence of Data Clouds Fusion From 3D Real-Time Vision System on Robotic Group Dead Reckoning in Unknown Terrain
- Effect of a Traffic Speed Based Cruise Control on an Electric Vehicle’s Performance and an Energy Consumption Model of an Electric Vehicle
- Proximity Based Automatic Data Annotation for Autonomous Driving
