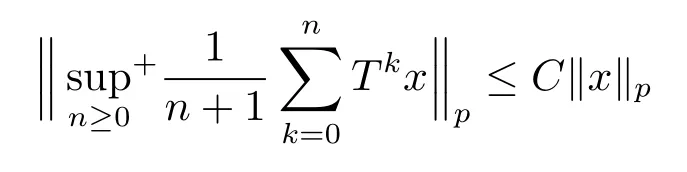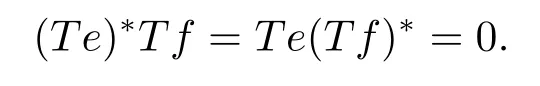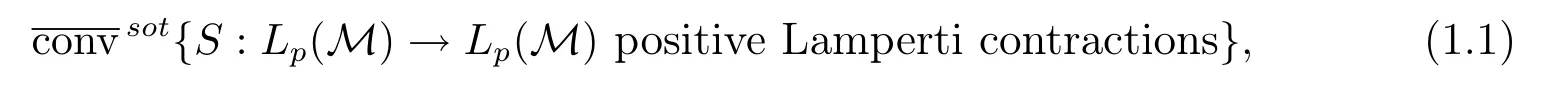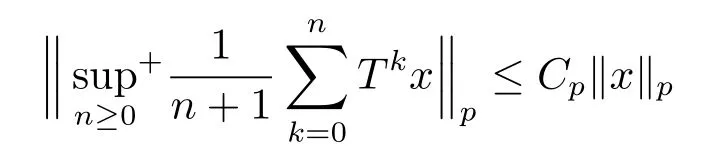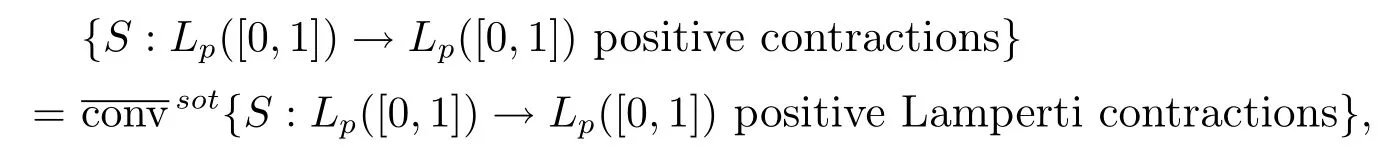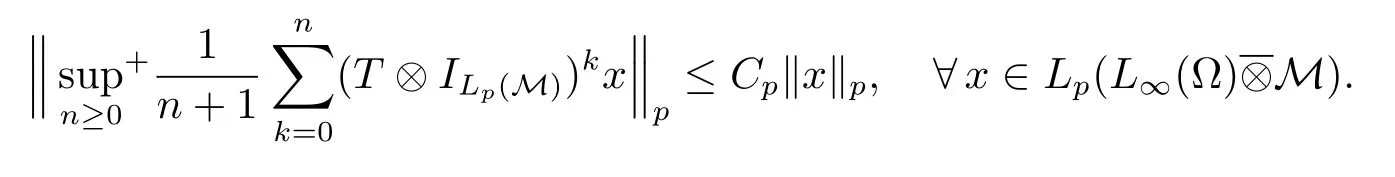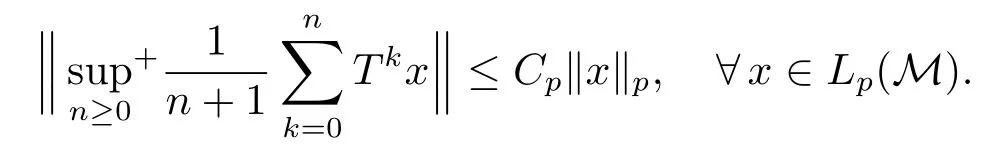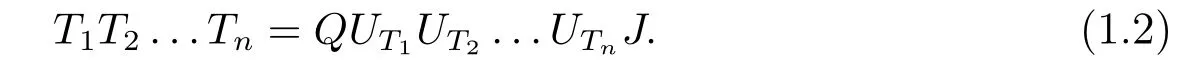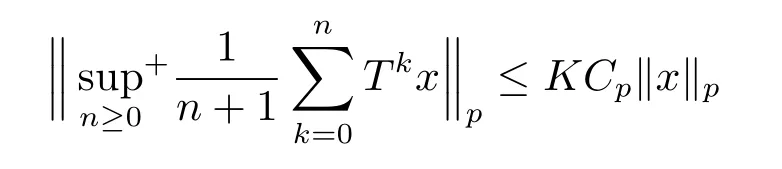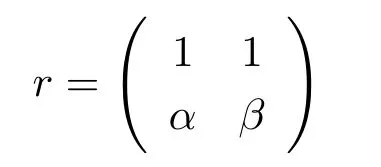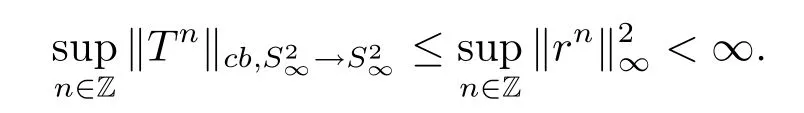RESEARCH ANNOUNCEMENTS ON“MAXIMAL ERGODIC INEQUALITIES FOR SOME POSITIVE OPERATORS ON NONCOMMUTATIVE LP-SPACE”
HONG Gui-xiang,RAY Samya Kumar,WANG Si-meng
(1.School of Mathematics and Statistics,Wuhan university,Wuhan 430072,China)
(1.Universié Paris-Saclay,CNRS,Laboratoire de mathématiques d’Orsay,Orsay 91405,France)
1 Introduction and Main Results
In classical ergodic theory,one of the earliest pointwise ergodic convergence theorems was obtained by Birkho ff[1]in 1931.Dunford and Schwartz[2]greatly generalized the previous situation;they established the strong(p,p)maximal inequalities for all1 Motivated by quantum physics,noncommutative mathematics have advanced in a rapid speed.As foundations of noncommutative mathematics,let us recall briefly the definition of noncommutativeLpspaces.LetMbe a von Neumann algebra equipped with a normal semifinite faithful traceτ.We denote bys(x)the support ofxfor a positive elementx∈M.LetS(M)be the linear span of set of all positive elements inMsuch thatτ(s(x))<∞.For1≤p<∞,we define the noncommutativeLp-spaceLp(M,τ)to be the completion ofS(M)with respect to the norm We refer the reader to[5]for detailed presentation of noncommutativeLpspaces. The connection between ergodic theory and von Neumann algebras is intimate and goes back to the earlier development of the theory of rings of operators.However,the study of pointwise ergodic theorems only took o ffwith the pioneering work of Lance[6].The topic was then stupendously studied in a series of works due to Conze,Dang-Ngoc,Kümmerer,Yeadon and others.However,the maximal inequalities and pointwise ergodic theorems inLp-spaces remained out of reach for many years until the path-breaking work of Junge and Xu[7].In[7],the authors established a noncommutative analogue of Dunford-Schwartz maximal ergodic theorem.This breakthrough motivated further research to develop various noncommutative ergodic theorems.We refer to[8,9]and references therein.Notice that the general positive contractions considered by Akcoglu do not fall into the category of Junge-Xu[7].In the noncommutative setting,there are very few results for operators beyondL1-L∞contractions except some isolated cases studied in[8].In particular,the following noncommutative analogue of Akcoglu’s maximal ergodic inequalities remains open. Question 1.1LetMbe a von Neumann algebra equipped with a normal faithful semifinite traceτ.Let1 for allx∈Lp(M)? In the article[10],we answer Question 1.1 for a large class of positive contractions which do not fall into the category of aforementioned works.Indeed,this class recovers all positive contractions concerned in Question 1.1 ifMis the classical spaceL∞([0,1]).To introduce our main results we set some notation and definitions. Definition 1.2Let1≤p<∞.A bounded linear mapT:Lp(M,τ)→Lp(M,τ)is called a Lamperti(or support separating)operator,if for any twoτ-finite projectionse,f∈Mwithef=0,we have that By the standard approximation argument,it is easy to observe that the above definition of Lamperti operators agrees with the known definition in the commutative setting. The following is one of our main results.We will denote byCpa fixed distinguished constant depending only onp,which is given by the best constant of Junge-Xu’s maximal ergodic inequality[7,Theorem 0.1]. Theorem 1.3Let1 that is,the closed convex hull of all positive Lamperti contractions onLp(M)with respect to the strong operator topology.Then for allx∈Lp(M). It is worth noticing that the class introduced in(1.1)is quite large in the classical setting.Indeed,it is known that forM=L∞([0,1])equipped with the Lebesgue measure,we have which does recover the classical Akcoglu’s ergodic theorem onLp([0,1]).Moreover,our methods also help to establish a completely bounded version of Ackoglu’s ergodic theorem. Corollary 1.4Let1 As mentioned earlier,Akcoglu’s arguments for ergodic theorem essentially rely on the study of dilations of positive contractions.In spite of various works on dilations on von Neumann algebras,Junge and Le Merdy showed in their remarkable paper[11]that there is no ‘reasonable’analogue of Akcoglu’s dilation theorem on noncommutativeLp-spaces.This becomes a serious difficulty in establishing a noncommutative analogue of Akcoglu’s ergodic theorem.Our proof of the above theorem is based on the study of structural properties and dilations of convex combinations of Lamperti operators as in(1.1).This route seems to be different from that of Akcoglu’s original one.Let us mention some of the key steps and new ingredients in the proof,which might be of independent interest. (i)Noncommutative ergodic theorem for positive isometries:Following the classical case,the first natural step would be to establish a maximal ergodic inequality for positive isometries.Here we give an analogue of this result in the noncommutative setting. Theorem 1.5Let1 Then The key ingredient is to extend positive isometries onLp(M)to the vector-valued spaceLp(M;‘∞).This fact seems to be highly non-obvious for the isometry not completely isometric.Then based on the methods recently developed in[8],we obtain Theorem 1.5. (ii)Structural theorems for Lamperti operators:In the classical setting,Peller and Kan obtained a dilation theorem for Lamperti contractions.Their constructions are different from Akcoglu’s and rely on structural description of Lamperti operators.In the noncommutative setting,we first prove a similar characterization for Lamperti operators by using techniques from[12],which constitutes the second step in proving Theorem 1.3. Theorem 1.6Let1≤p<∞.LetT:Lp(M,τ)→Lp(M,τ)be a Lamperti operator with normC.Then,there exist,uniquely,a partial isometryw∈M,a positive self-adjoint operatorbaffiliated withMand a normal Jordan?-homomorphismJ:M→M,such that (i)w?w=J(1)=s(b);moreover we havew=J(1)=s(b)if additionallyTis positive; (ii)Every spectral projection ofbcommutes withJ(x)for allx∈M; (iii)T(x)=wbJ(x),x∈S(M); (iv)We haveτ(bpJ(x))≤Cτ(x)for allx∈M+;if additionallyTis isometric,then the equality holds withC=1. (iii)Dilation theorem for the convex hull of Lamperti contractions:In order to establish ergodic theorems for a large class beyond Lamperti contractions,as the last step,we deploy tools from[13]to obtain anN-dilation theorem for the convex hull of Lamperti contractions for allN∈N. Definition 1.7Let1≤p≤∞.LetS?B(Lp(M,τM)).We say thatShas a simultaneousN-dilation if there exist a von Neumann algebraNwith a normal faithful semifinite traceτN,contractive linear mapsQ:Lp(N,τN)→Lp(M,τM),J:Lp(M,τM)→Lp(N,τN),and a set of isometriesU?Lp(N,τN)such that for alln∈{0,1,...,N}andTi∈S,1≤i≤n,there existUT1,UT2,...,UTn∈Usuch that In terms of commutative diagram,we have The empty product(i.e.n=0)corresponds to the identity operator. Theorem 1.8Let1 Then,each operatorT∈conv(S)has aN-dilation for allN∈N. In the process,we actually prove a simultaneous dilation theorem for tuples of Lamperti contractions,that is,for allN∈N,which is a stronger version of Peller-Kan’s dilation theorem.Our approach also establishes validity of noncommutative Matsaev’s conjecture for the strong closure of the closed convex hull of Lamperti contractions for1 Note that Theorem 1.3 only applies to contractive operators.As in the classical case,the study for non-contractive power bounded operators requires many additional e ff orts.In the following we also establish a general ergodic theorem for power bounded Lamperti operators as soon as their adjoints are also Lamperti(usually called doubly Lamperti operators),which is the other main result of the paper. Theorem 1.9Let1 for allx∈Lp(M). The above theorem 1.9 is the noncommutative analogue of a classical result of Kan[4].It essentially relies on a structural theorem for positive doubly completely Lamperti operators,which reduces the problem to the setting of Theorem 1.3 and is of independent interest. Theorem 1.10LetMbe a finite von Neumann algebra.Let1 (i)Sis a positive Lamperti contraction which vanishes onLp(p0Mp0)and is isometric onLp(p1Mp1); (ii)θnis a positive element inMof the formθn=θJ(θ)···Jn?1(θ)andθnSn(x)=Sn(x)θnfor alln≥1andx∈M; (iii)for alln≥1,kTnkLp(M)→Lp(M)≤kθnk∞.Moreover,the equality holds if the adjoint operatorT?:Lp0(M)→Lp0(M)for1/p+1/p0=1is also Lamperti. To prove this structural result,we follow the path of Kan.However,since the structures and orthogonal relations of von Neumann subalgebras are completely different from those in classical measure theory,our proof is much more lengthy and numerous adjustments are needed in this new setting.Also,due to these technical reasons,we restrict our study to the case of finite von Neumann algebras only. Moreover,we observe that the maximal ergodic inequality also holds for several other classes of operators outside the scope of Theorem 1.3 or Theorem 1.9. (i)Positive invertible operators which are not Lamperti:Kan[4]discussed various examples of Lamperti operators.He showed that in the classical setting any positive invertible operator with positive inverse is Lamperti and that any positive invertible operator on a finite dimensional(commutative)Lp-space withsupn∈ZkTnkLp→Lp<∞is Lamperti..As a consequence,he reproved that any power bounded positive operator with positive inverse admits a maximal ergodic inequality;this generalized the ergodic theorem of de la Torre.A noncommutative analogue of this theorem,in a much general form,was achieved in[8].However,we provide the following example of positive invertible operators on noncommutativeLp-spaces with positive inverses which are not even Lamperti,which illustrates that there is no reasonable analogue of Kan’s above examples for the noncommutative setting. Example 1.11Let1≤p<∞andrbe an invertible matrix2×2matrix.DefineClearly,Tis completely positive map,and so is the inverse mapT?1(x)=r?1x(r?1)?.Note that are two orthogonal projections withef=fe=0.But if we take withα,β∈R,and1+0,it is easy to see thatT(e)T(f)0.SoTis not Lamperti. Moreover,considerα=0,β=?1.Thenr?1=randr2=1M2.So Since the operator space of linear operators onM2is finite dimensional,so(Tk)is uniformly bounded with respect to any equivalent operator norm.Thus these are power bounded positive operators with positive inverses on a finite dimensionalLp-space,but not Lamperti. This shows that Kan’s method can not reprove de la Torre’s ergodic theorem in the noncommutative setting.Nevertheless,these examples fall into the category of the aforementioned result of[8],and hence satisfy the maximal ergodic theorem.We would like to remark that Kan’s aforementioned examples of Lamperti operators play an important role in many other papers.All these phenomena seem to be new. (ii)Junge-Le Merdy’s non-dilatable example:As mentioned earlier,there exist concrete examples of completely positive complete contractions which fail to admit a noncommutative analogue of Akcoglu’s dilation,constructed by Junge and Le Merdy[11].While we show that these operators still satisfy a maximal ergodic inequality.In particular we establish the following fact. Proposition 1.12Let12<∞.Then,for allk∈Nlarge enough,there exists a completely positive complete contractionsuch that butTdoes not admit Ackoglu’s dilation. The proof is very short and elementary;indeed it still relies on Akcoglu’s ergodic theorem[3]in the classical setting.The above theorem illustrates again that the noncommutative situation is significantly different from the classical one. For the proof of all the results mentioned above,we refer the reader to[10]for more information.