阿貝爾hom-李環(huán)擴(kuò)張的自同構(gòu)
徐曉寧賴 燕
(1.遼寧大學(xué)數(shù)學(xué)院,遼寧沈陽 110036)
(2.信陽大別山高級中學(xué),河南信陽 464000)
1 引言
近些年來,hom-結(jié)構(gòu),如hom-李代數(shù),hom-代數(shù),hom-李超代數(shù),hom-超代數(shù),hom-雙代數(shù),n-元hom-Nambu-李代數(shù)以及hom-李2-代數(shù)等代數(shù)結(jié)構(gòu)及性質(zhì)被廣泛研究,而且取得了許多重要研究結(jié)果.hom-李代數(shù)最早是由Hartwig,Larsson以及Silvestrov在文獻(xiàn)[1]中研究Witt代數(shù)和Virasoro代數(shù)的形變時(shí)提出來的.文獻(xiàn)[2]給出了hom-李代數(shù)及其表示的定義,而且對hom-李代數(shù)的表示理論進(jìn)行了嚴(yán)謹(jǐn)細(xì)致的研究.文獻(xiàn)[3]在半單李代數(shù)上研究了hom-李代數(shù)的結(jié)構(gòu).二次hom-李代數(shù)在文獻(xiàn)[4]中得到了研究.文獻(xiàn)[5]提供了保積hom-李代數(shù)可解的充要條件.
而在李理論的研究中,李環(huán)是一個(gè)重要且非常有趣的課題.在文獻(xiàn)[6]中,研究了冪零李環(huán)的條件及冪零李環(huán)的中心序列.對于4-Engel李環(huán)的冪零類的研究在文獻(xiàn)[7]中得到體現(xiàn).文獻(xiàn)[8,9]對李環(huán)的二階上同調(diào)及Schreier’s擴(kuò)張理論進(jìn)行了探索.特別的,在文獻(xiàn)[10]中,作者在李環(huán)的一個(gè)短正合序列中的A的擴(kuò)張的自同構(gòu)群上構(gòu)造正合序列,這里A是E的阿貝爾子環(huán).他們通過一系列的研究得出如下結(jié)論.
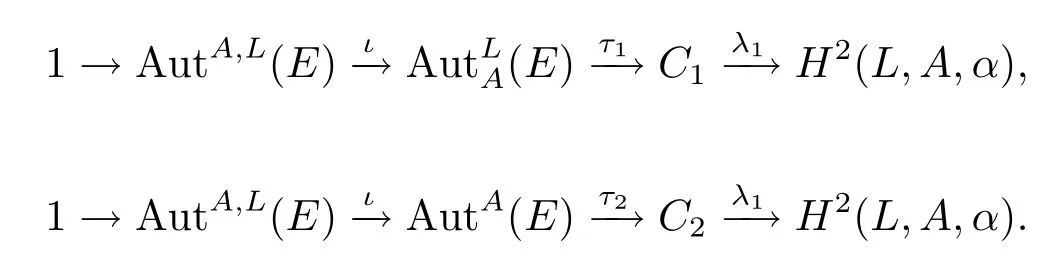
設(shè)A→E→L是中心擴(kuò)張,則存在以下正合序列
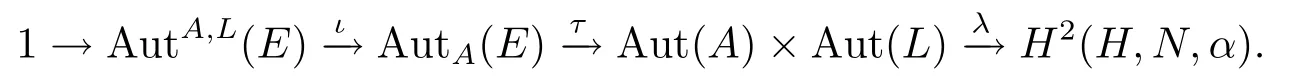
文獻(xiàn)[11,12]研究了有限維p-群上的p-自同構(gòu).文獻(xiàn)[13,14]分別在群擴(kuò)張的自同構(gòu)中得到了一個(gè)正合序列和在群擴(kuò)張的自同構(gòu)群上得到Wells正合序列.特別地,在文獻(xiàn)[15]中,作者在群的一個(gè)短正合序列中的N的擴(kuò)張的自同構(gòu)群上構(gòu)造正合序列,這里N是G的阿貝爾子群.他們通過一系列的研究得出如下結(jié)論.

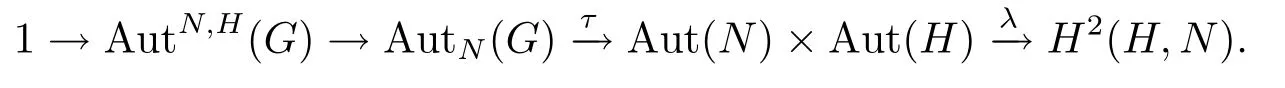
文獻(xiàn)[16]首次研究了hom-李環(huán),給出了hom-李環(huán)的定義并討論了hom-李環(huán)冪零的條件.自然地,通過對阿貝爾群擴(kuò)張的自同構(gòu)和阿貝爾李環(huán)擴(kuò)張的自同構(gòu)的研究,希望在阿貝爾hom-李環(huán)中也能構(gòu)造出相應(yīng)的正合序列,并對其進(jìn)行相關(guān)應(yīng)用.本文具體結(jié)果如下:
定理1.1令是一個(gè)阿貝爾擴(kuò)張,則有以下兩個(gè)正合序列:
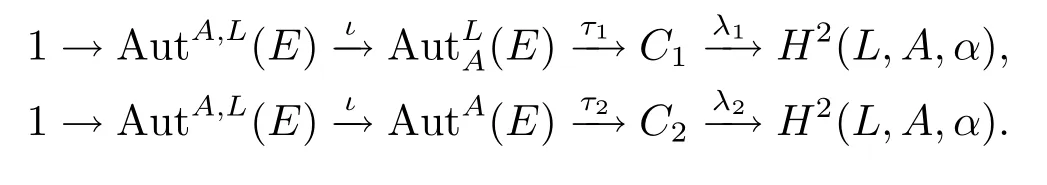
定理1.2令是一個(gè)中心擴(kuò)張,則存在下列正合序列:
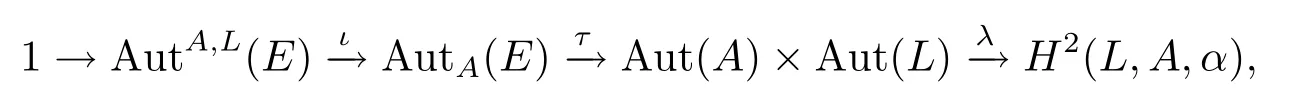
定理1.3令E是一個(gè)hom-李環(huán),且A是E的一個(gè)阿貝爾理想,如果序列A→E→L分裂,則序列
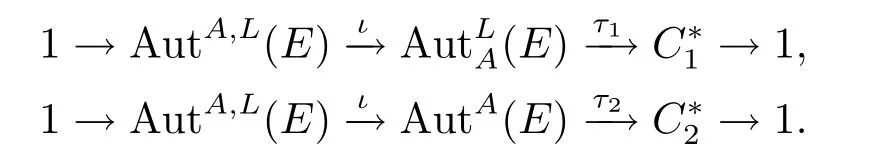
也可裂.
定理1.4令E是一個(gè)階為pn(p≥2)的hom-李p環(huán),Z(E)是循環(huán)的且Φ(E)?Z(E).則每一個(gè)Z(E)的p自同構(gòu)都可以被擴(kuò)張成依賴于的E上的自同構(gòu),這里,A=Z(E),L=E/Z(E).
本文內(nèi)容安排如下.第2節(jié)介紹與hom-李環(huán)及其正合序列等有關(guān)的一些基本概念.第3節(jié),在是阿貝爾hom-李環(huán)擴(kuò)張的前提下,討論了正合序列的實(shí)現(xiàn)過程,并給出了不同情況下的正合序列.在阿貝爾hom-李環(huán)擴(kuò)張是可分裂的情況下,對不同形式擴(kuò)張下的正合序列進(jìn)行了改造,使得被改造后的正合序列依然可分裂.第4節(jié),對定理3.10中所得到的正合序列(3.4)進(jìn)行了應(yīng)用.
2 定義
本節(jié)給出本文中將涉及的一些相關(guān)概念和基本結(jié)論.
定義2.1[16]hom-李環(huán)是指一個(gè)三元數(shù)組(L,[·,·],β),其中L是一個(gè)阿貝爾群,[·,·]:L×L→L是反對稱雙線性映射,線性映射β:L→L滿足hom-Jacobi等式
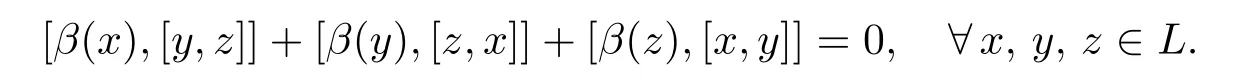
定義2.2設(shè)(L,[·,·],β)為hom-李環(huán),若線性映射β:L→L滿足
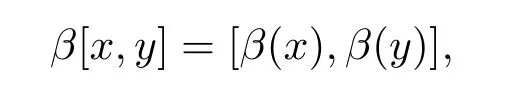
其中x,y∈L. 則稱 (L,[·,·],β)為保積 hom-李環(huán).
定義2.3設(shè) (L,[·,·],β)是一個(gè) hom-李環(huán),并且M為L的子群. 若β(M)?M,[M,M]?M,則稱 (M,[·,·],β)是 (L,[·,·],β)的 hom- 子環(huán).若L的子群M滿足β(M)?M,[M,L]?M, 稱M為 (L,[·,·],β)的理想.
定義2.4設(shè)L為有限維hom-李環(huán),若0令Φ(L)為L的所有極大hom-子環(huán)的交.若L=0,令Φ(L)=0,則稱Φ(L)是L的Frattini hom-子環(huán).
定義2.5設(shè) (L,[·,·],β)是一個(gè)保積的hom-李環(huán),令βk=β?β?···?β,特別地β0=id,β1=β,對于任一非負(fù)整數(shù)k,一個(gè)線性映射D:L→L,如果滿足下面兩個(gè)條件
(1)[D,β]=0,
(2)D([x,y])=[D(x),βk(y)]+[βk(x),D(y)],?x,y∈L.
則稱D為hom-李環(huán)的βk導(dǎo)子.所有的hom-李環(huán)的βk導(dǎo)子的集合記為Derβk(L).
定義2.6定義hom-李環(huán) (L,[·,·],β)的降中心列為
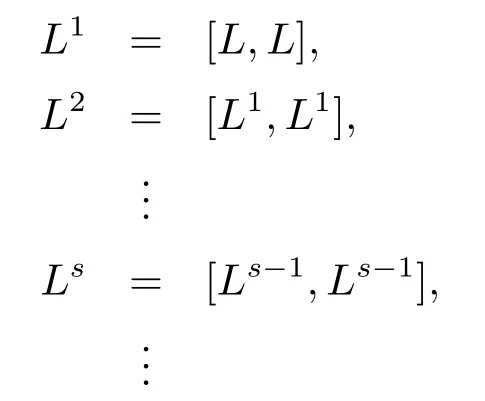
若存在n∈Z+,使得Ln=0,則 稱 (L,[·,·],β)冪零.
定義2.7令L是一個(gè)hom-李環(huán)且n∈N+,定義
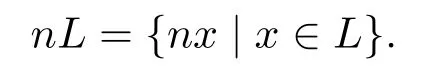
則易知nL是L的一個(gè)理想.一個(gè)冪零hom-李環(huán)L的階為p,稱L為p-hom-李環(huán).稱L0=[L,L]為L的導(dǎo)出子環(huán).
定義2.8設(shè) (L1,[·,·],β1)與 (L2,[·,·],β2)為 hom-李環(huán).若線性映射φ:L1→L2滿足
(1)β2φ=φβ1,
(2)φ([x,y]1)=[φ(x),φ(y)]2,?x,y∈L1,
則稱φ為hom-李環(huán)同態(tài).當(dāng)φ既是單射又是滿射時(shí),則稱它為同構(gòu)映射.
定義2.9設(shè)(L,[·,·],β)是一個(gè)hom-李環(huán),N是L的理想.L/N={x+N|x∈L}在L/N的元素之間定義方括號積[·,·]如下
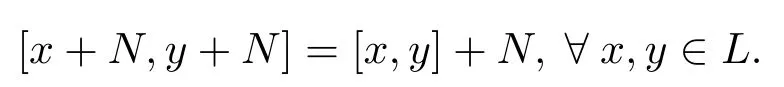
若是L/N上的一個(gè)同態(tài)且則L/N關(guān)于上述方括號積構(gòu)成一個(gè)hom-李環(huán),稱L/N為hom-李環(huán)L模掉理想N的商環(huán),記為=L/N.
定義2.10若E→L是hom-李環(huán)的滿同態(tài),所以對?x∈L,則存在tx∈E,使得tx→x,稱tx為x的一個(gè)提升.
定義2.11設(shè)L1,L2,···,Lk,···均為域F上的hom-李環(huán),又fi是Li到Li+1的同態(tài).如果 Kerfi+1=fi(Li),i=1,2,···,則稱序列
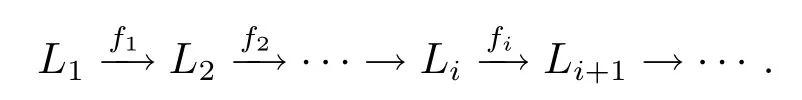
為正合序列.
定義2.12設(shè)(L,[·,·],β)是一個(gè)hom-李環(huán),V是線性空間,并且βv是V上的線性映射.(V,βv)就被稱為hom-L-模,如果存在一個(gè)映射
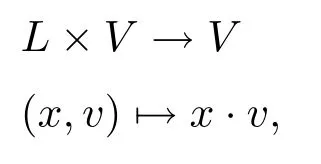
并且?v∈V,x,y∈L,滿足以下條件
(1)βv(x·v)=β(x)βv(v),
(2)[x,y]βv(v)=β(x)yv?β(y)xv.
定義2.13設(shè)a,b與L均為hom-李環(huán),若有L的理想n與a同構(gòu),而商環(huán)L/n與b同構(gòu),則稱L是b通過a的擴(kuò)張.
定義2.14設(shè)L是一個(gè)hom-李環(huán),A是一個(gè)平凡的hom-L-模,令Z2(L,A,α)是所有函數(shù)對(f,g,α)的集合.這里f,g:L×L→A,α:L→Derβk(A),對?l,l1,l2,l3∈L滿足
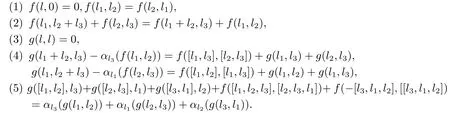
稱Z2(L,A,α)為在A上的L上的上閉鏈.
現(xiàn)給出兩個(gè)上閉鏈 (f,g,α),(f0,g0,α)∈Z2(L,A,α),令 (f,g,α)+(f0,g0,α):=(f+f0,g+g0,α),這里f+f0,g+g0在逐點(diǎn)加法(如果f,g:L×L→A,則(f,g,α)(l1,l2)=f(l1,l2)+g(l1,l2))的運(yùn)算下構(gòu)成阿貝爾群.
定義2.15設(shè)L是一個(gè)hom-李環(huán),A是一個(gè)平凡的hom-L-模,令t:L→A是一個(gè)滿足t(0)=0的映射.且令B2(L,A,α)是所有函數(shù)對(f,g,α)的集合.這里f,g:L×L→A,α:L→DerβK(A),對?l1,l2∈L滿足
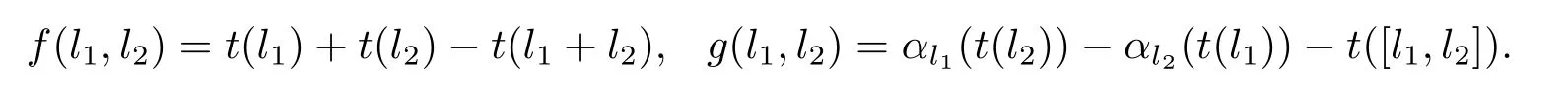
稱函數(shù)對(f,g,α)為在A上的L上的邊界余映射.
不難證明B2(L,A,α)是Z2(L,A,α)的子集.
定義2.16稱商群H2(L,A,α)=Z2(L,A,α)/B2(L,A,α).為hom-李環(huán)L的二階上同調(diào)群.
定義2.17一個(gè)被阿貝爾hom-李環(huán)A的被hom-李環(huán)L的擴(kuò)張0→A→Eπ?→L→0稱為是可裂的.如果存在一個(gè)hom-李環(huán)同態(tài)λ:L→E使得πλ=1L.
3 正合序列及分裂正合序列的構(gòu)造
本節(jié)的目的是構(gòu)造阿貝爾hom-李環(huán)的正合序列,由于hom-李環(huán)本身內(nèi)部存在一個(gè)映射和兩種運(yùn)算并且還具有復(fù)雜的二階上同調(diào)群,顯然會(huì)比群和李環(huán)的構(gòu)造更加復(fù)雜.在定理3.10和3.12的基礎(chǔ)之上通過阿貝爾李擴(kuò)張推廣了三個(gè)正合序列,并證明了在序列可裂的情況下所推廣的這三個(gè)正合序列也可裂.
令E和L是保積hom-李環(huán),A是E的理想.β:L→L限制在A上是A上的線性變換,β是同態(tài)映射且與γ,π可交換,這一規(guī)定貫穿全文.首先來介紹一些記號.
定義3.1[10]令
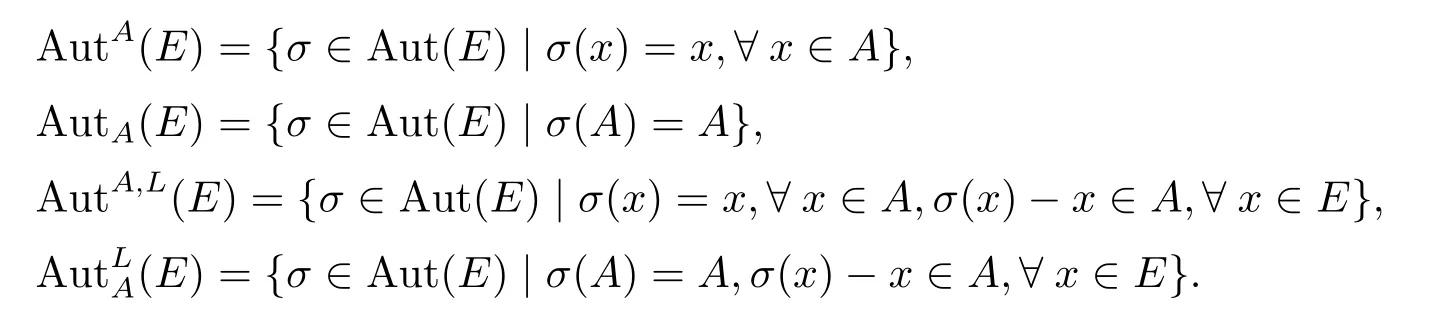
引理3.1設(shè)是一個(gè)阿貝爾hom-李環(huán)擴(kuò)張,其中A是E的阿貝爾子環(huán).則阿貝爾hom-李環(huán)A的被hom-李環(huán)E的一個(gè)擴(kuò)張確定了E到A的自同構(gòu)群Aut(A)的一個(gè)hom-李環(huán)同態(tài).
證設(shè)正合列0→A→E→L→1是阿貝爾hom-李環(huán)A的被hom-李環(huán)E的一個(gè)擴(kuò)張.則E→L是滿同態(tài),進(jìn)而對?x∈L,都存在一個(gè)提升tx∈E,即tx→x.于是可以規(guī)定
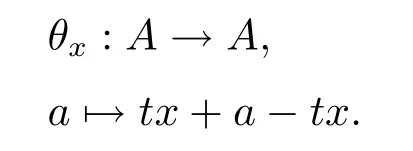
又因?yàn)锳是E的hom-李環(huán),所以Im(θx)?A,當(dāng)然θx是A的一個(gè)自同構(gòu).從而存在
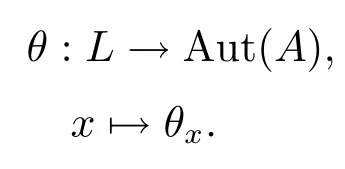
接下來利用α(l)=αl,這里αl(a)=[βk(l),a],l∈L,a∈A,來定義一個(gè)hom-李環(huán)同態(tài)α:L→Derβk(A).所以,可以考慮第二上同調(diào)群H2(L,A,α).與群和李環(huán)的情況類似,對于任意的阿貝爾擴(kuò)張(θ,φ)∈Aut(A)×Aut(L)被稱為是相容的,如果?l∈L,滿足θαlθ?1=αφ(l).把所有的相容對記為C.類似于阿貝爾群擴(kuò)張的Wells序列及阿貝爾李環(huán)擴(kuò)張的正合序列,對每一個(gè)γ∈AutA(E)都包含了一個(gè)相容對(θ,φ),而且映射τ(γ)=(θ,φ)是一個(gè)同態(tài).令是一個(gè)阿貝爾hom-李環(huán)擴(kuò)張,其中A是E的阿貝爾子環(huán).設(shè)t:L→E是E的一個(gè)正規(guī)截口.則對任意的l∈L,必存在一個(gè)x∈E使得π(x)=l,而且t(l)由A+t(l)=A+x所確定.這就說明了π(t(l))=l成立.
對?l1,l2∈L,定義
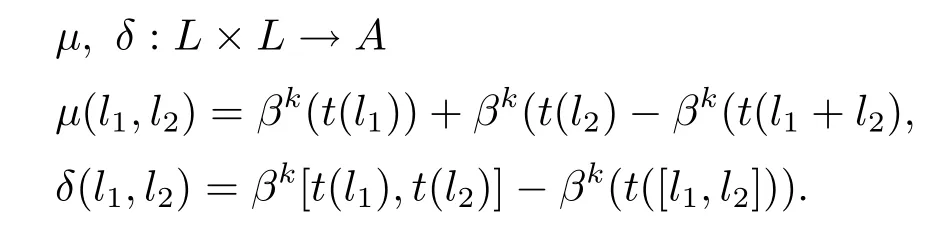
引理 3.2根據(jù)以上定義,則有 (μ,δ,α)∈Z2(L,A,α).
證要證(μ,δ,α)∈Z2(L,A,α),只需要證對?l1,l2,l3∈L有以下等式成立即可
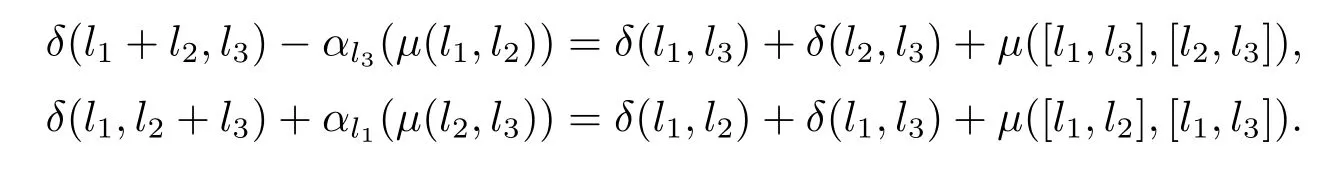
由于

且
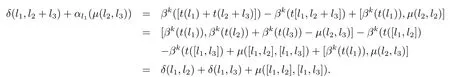
故有 (μ,δ,α)∈Z2(L,A,α).證畢.
引理3.3令A(yù)→Eπ?→L是一個(gè)阿貝爾擴(kuò)張,若σ∈AutA(E),則存在一個(gè)三元組(θ,φ,χ)∈Aut(A)×Aut(L)×AL,使得對任意的l,l1,l2∈L,a∈A.有下列等式成立
(i)γ(βk(t(l)+a))=βk(t(φ(l)))+χ(l)+θ(a),
(ii)μ(φ(l1),φ(l2))?θ(μ(l1,l2))=χ(l1+l2)?χ(l1)?χ(l2),
(iii)θ[βk(t(l)),a]=[βk(t(φ(l))),θ(a)],
(iv)δ(φ(l1),φ(l2))?θ(δ(l1,l2))=χ[l1,l2]?[χ(l1),βk(t(φ(l2)))]?[βk(t(φ(l1))),χ(l2)].
證(i)令θ=γ|A,定義φ:L→L使得對任意的l∈L,滿足φ(l)=π(γ(t(l))).顯然θ∈Aut(A),φ∈Aut(L).
現(xiàn)在進(jìn)一步定義χ∈AL,由于對任意的l∈L,都有π(t(l))=l,故有π(t(φ(l)))=φ(l),所以π(t(φ(l)))?φ(l)=0.由此,定義χ:L→A滿足χ(l)=βk(γ(t(l)))?βk(t(φ(l))).現(xiàn)在令l∈L,a∈A,則 得到γ(βk(t(l)+a))=γ(βk(t(l)))+θ(a)=χ(l)+βk(t(φ(l)))+θ(a).
(ii)令l1,l2∈L,根據(jù)定義有,
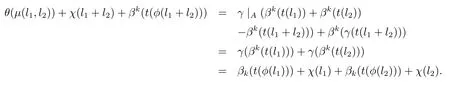
因此有,
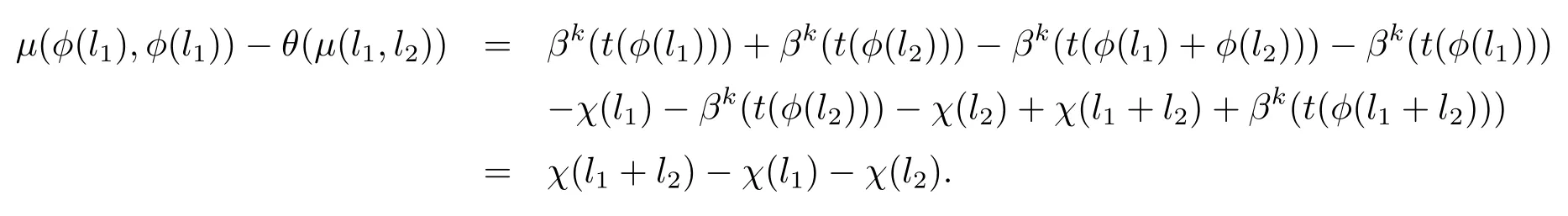
(iii)令l∈L,a∈A,故
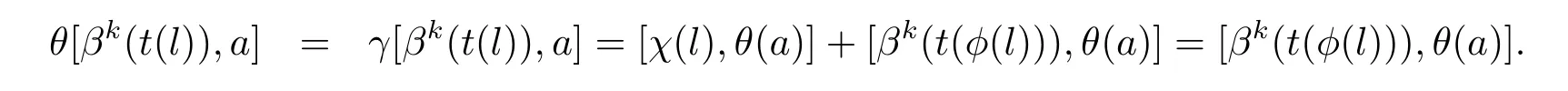
(iv)令l1,l2∈L,根據(jù)定義有,
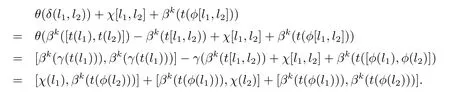
故有,
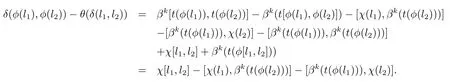
證畢.
引理3.4令是一個(gè)阿貝爾擴(kuò)張,若三元組(θ,φ,χ)∈Aut(A)×Aut(L)×AL滿足引理3.3中的(ii)–(iv),則由引理3.3的(i)定義的映射γ:E→E是屬于AutA(E)中的在E上的自同構(gòu).
證首先注意到對任意的x∈E,其都可以被表示為x=βk(t(l))+a的形式.令
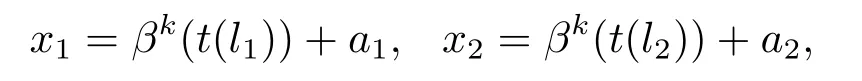
其中l(wèi)1,l2∈L,a1,a2∈A.故有,
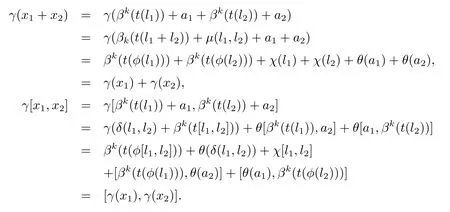
現(xiàn)在令x∈ker(γ),這里x=βk(t(l))+a,其中l(wèi)∈L,a∈A.這意表明βk(t(φ(l)))∈A或者說φ(l)=0,因此l=0.由此可知θ(a)=0,所以x=0.故該映射是單射.下證γ是滿射.令u∈E,則可以寫成u=βk(t(l0)+a0),其中l(wèi)0∈L,a0∈A.取l∈L,a∈A滿足:φ(l)=l0且θ(a)=a0?χ(l).故有,
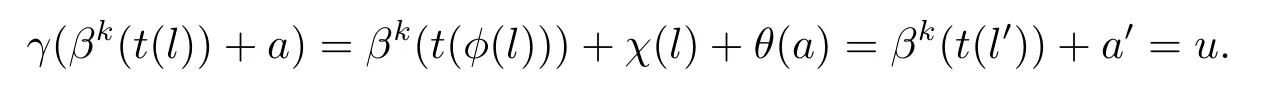
故該映射是滿射.證畢.
當(dāng)A?Z(E)時(shí),說是中心擴(kuò)張.若是一個(gè)中心擴(kuò)張,則L在A上的作用是平凡的,且引理3.3,3.4會(huì)有如下改變:
引理3.5令是中心擴(kuò)張,若γ∈AutA(E),則存在一個(gè)三元組(θ,φ,χ)∈Aut(A)×Aut(L)×AL對?l,l1,l2∈L,a∈A滿足
(i)γ(βk(t(l))+a)=βk(t(φ(l)))+χ(l)+θ(a),
(ii)μ(φ(l1),φ(l2))?θ(μ(l1,l2))=χ(l1+l2)?χ(l1)?χ(l2),
(iii)δ(φ(l1),φ(l2))?θ(δ(l1,l2))=χ[l1,l2].
引理3.6令是中心擴(kuò)張,若三元組(θ,φ,χ)∈Aut(A)×Aut(L)×AL滿足引理3.5中的(ii)和(iii),則由引理3.5的(i)定義的映射γ:E→E是屬于AutA(E)中的在E上的自同構(gòu).
引理3.7由所有的相容對組成的集合是Aut(A)×Aut(L)的子群.將所有相容對組成的子群記為C.并由此定義C1和C2如下
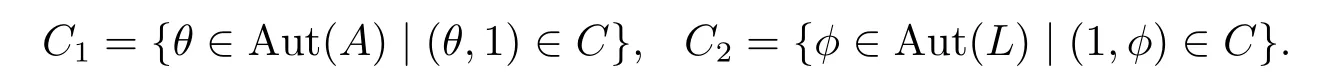
記
(i)θ∈C1?θαl=αlθ,?l∈L?θ[βk(t(l)),a]=[βk(t(l)),θ(a)],?l∈L,a∈A,
(ii)φ∈C2?αl=αφ(l),?l∈L?[βk(t(l)),a]=[βk(t(φ(l))),a],?l∈L,a∈A.
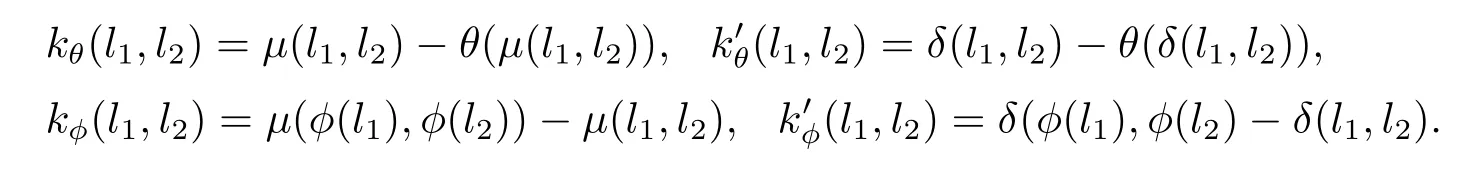
引理3.8根據(jù)以上定義是Z2(L,A,α)中的元素.
證要證只需要證對?l1,l2,l3∈L,有以下等式成立即可
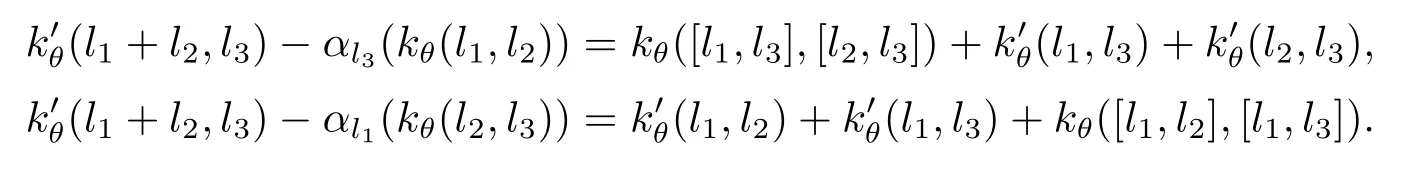
由引理3.2知以下等式成立
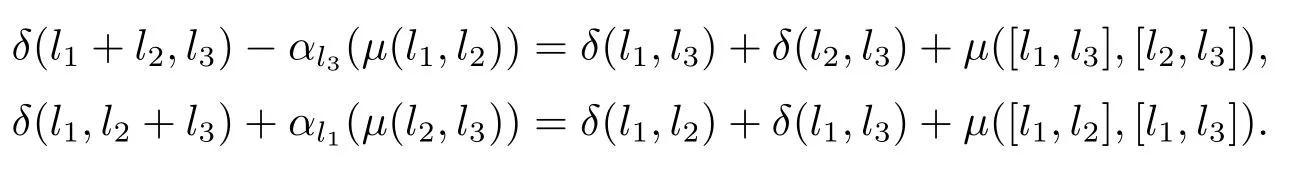
故有,
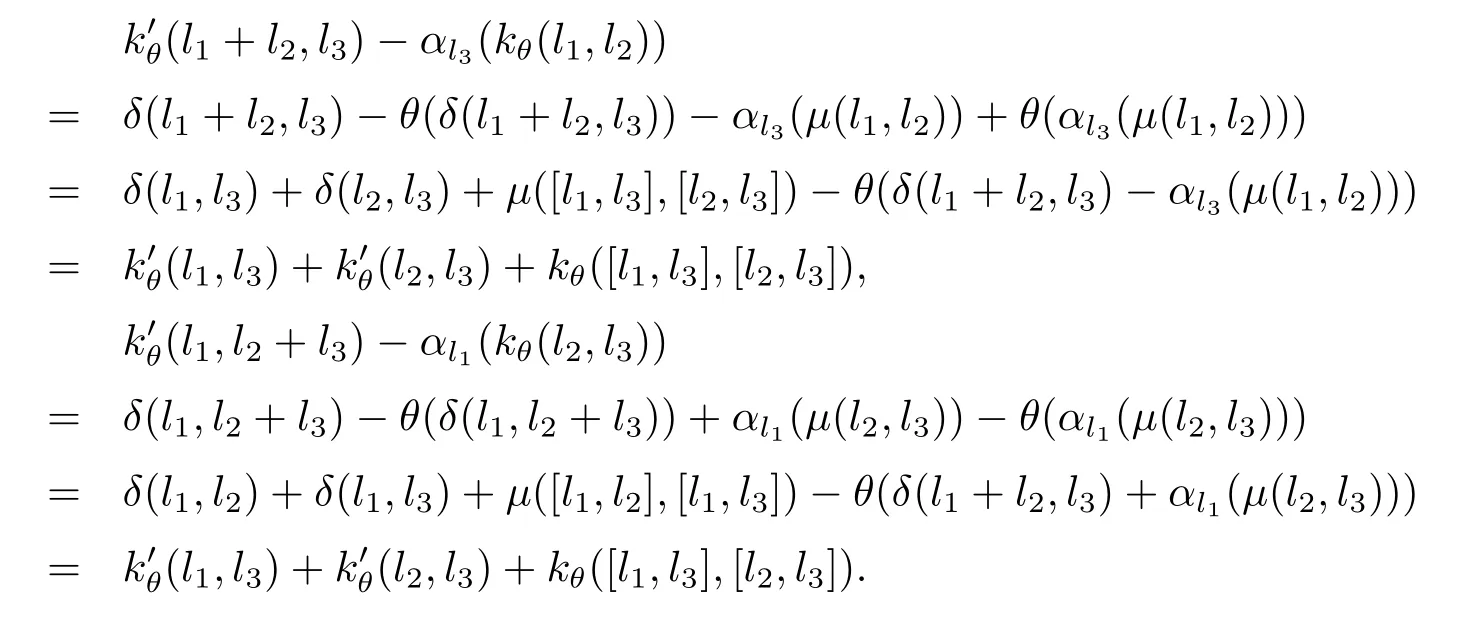
根據(jù)上面的假設(shè)和標(biāo)記,定義λi:Ci→H2(L,A,α)(i=1,2)如下
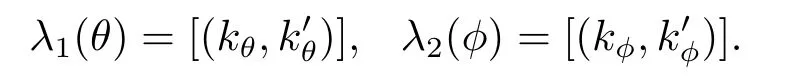
引理3.9映射λ1和λ2是定義明確的.
證首先證明λ1是定義明確的.令t,t0:L→E是兩個(gè)正常映射,則有t(l)?t0(l)∈A,?l∈L.因此對每一個(gè)l∈L都會(huì)唯一的存在λ(l)∈A使得:βk(t(l))=βk(t0(l))+λ(l).這就由等式:λ(l)=βk(t(l))+βk(t0(l)),定義了一個(gè)映射λ:L→A.又由于
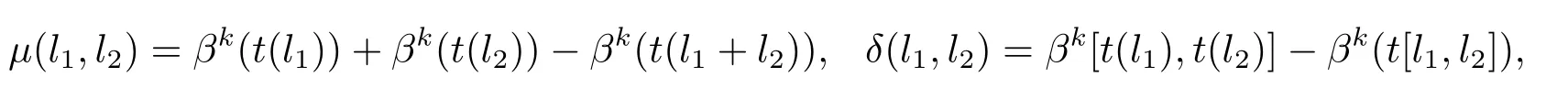
其中l(wèi)1,l2∈L.同樣地,考慮t0,得到兩個(gè)映射μ0,δ0:L×L→A.使得其滿足
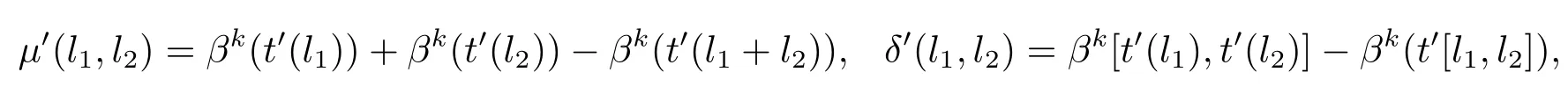
其中l(wèi)1,l2∈L,可以看出
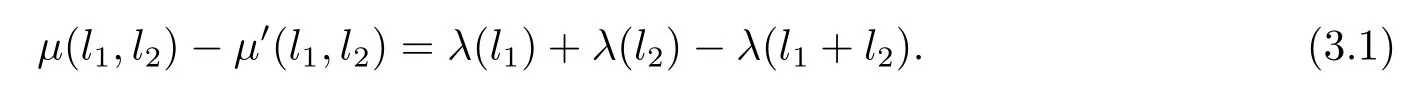
又由于
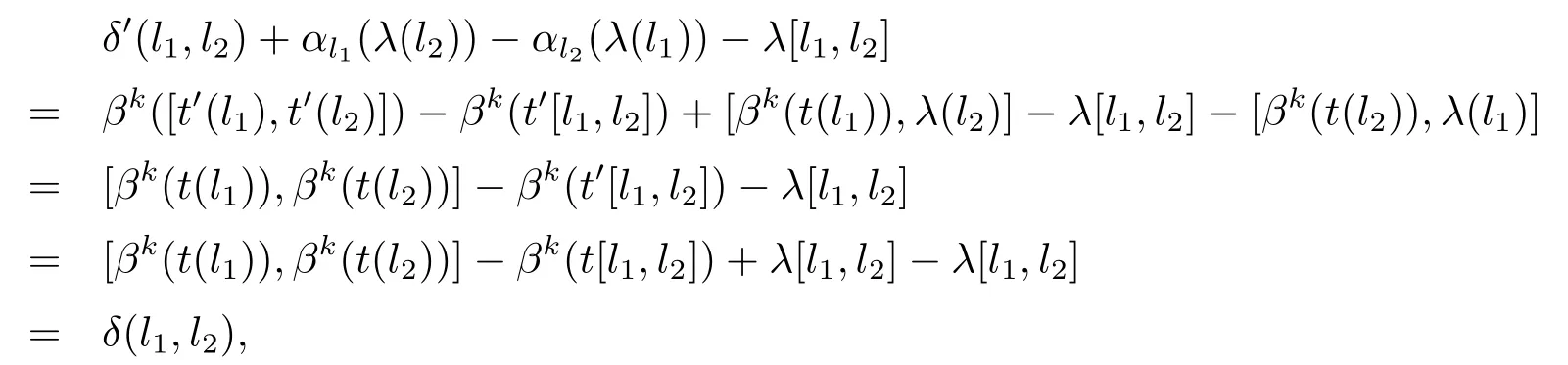
故有,
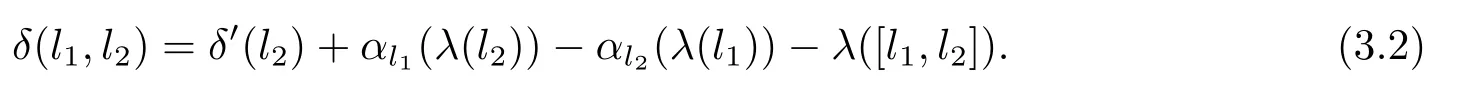
現(xiàn)在令θ∈C1且φ∈C2,定義映射使得其滿足
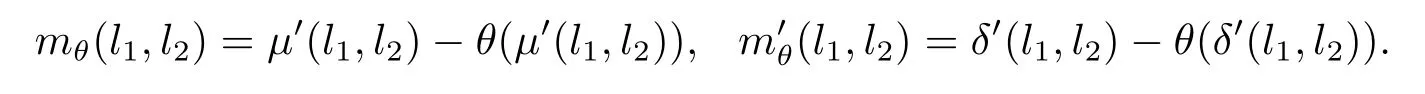
則由(3.1)式可知下面等式成立
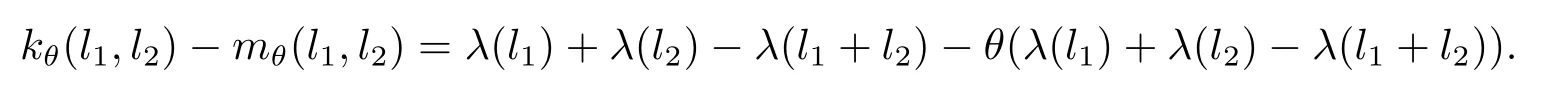
定義映射λ0:L→A使得其滿足對?l∈L都有,λ0(l)=λ(l)?(θλ)(l).自然地有,
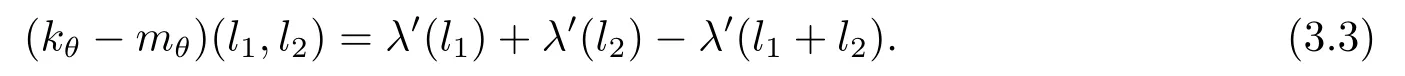
由(3.2)及θ∈C1,可以得知,
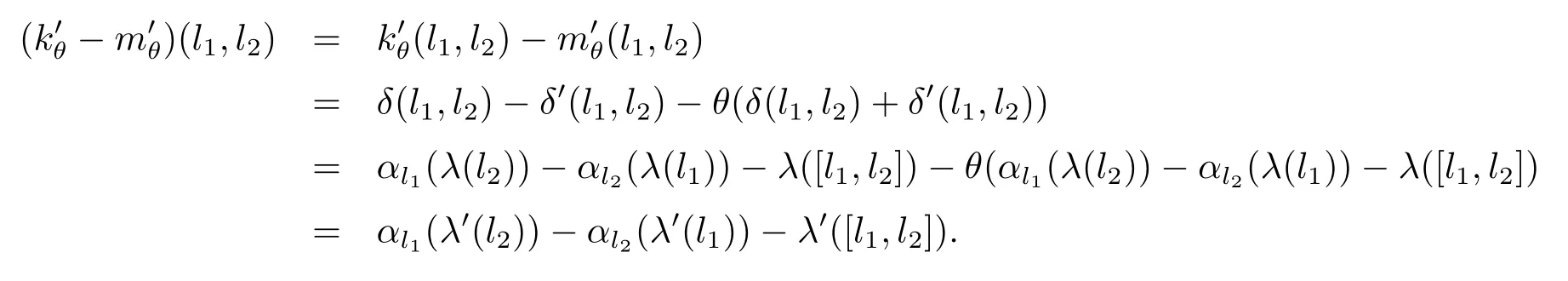
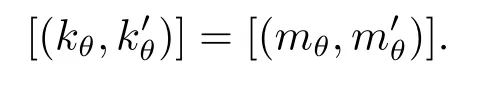
這就說明了λ1的選取不依賴于所取得空間.同理可證λ2.證畢.
注記:映射λ1,λ2不是同態(tài)映射,但這里Ker(λi)(1≤i≤2)與通常其所表示的意義一致.
定理3.10令是一個(gè)阿貝爾擴(kuò)張,則有以下兩個(gè)正合序列:
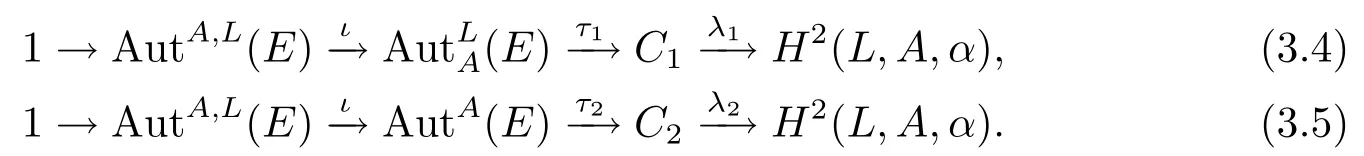
證先證(3.4),由于是顯然的.只需證即可.令有,這里θ=γ|A.因?yàn)橛?φ(l)=(πγt)(l)=l.又由引理3.3可知,

下面證明Ker(λ1)?Im(τ1).設(shè)θ∈C1且滿足λ1(θ)=1.則有因此存在一個(gè)映射χ:L→A,其中χ(0)=0,滿足等式
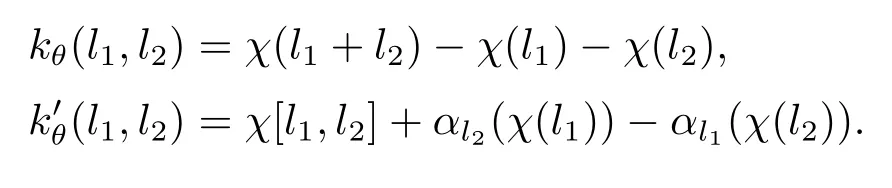
根據(jù)引理3.3,令φ=id|L,得到自同構(gòu)γ∈AutA(E)滿足
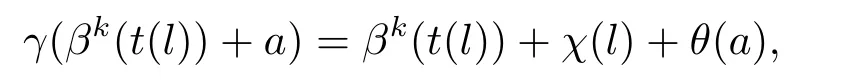
其中l(wèi)∈L,a∈A.因此有,
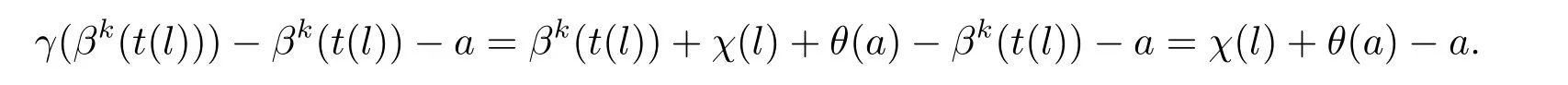
故γ(βk(t(l)))?(βk(t(l))+a)∈A.這就證明了進(jìn)一步有,γ(a)=θ(a),其中a∈A.所以τ1(γ)=θ.故Ker(λ1)?Im(τ1).因此是正合列.
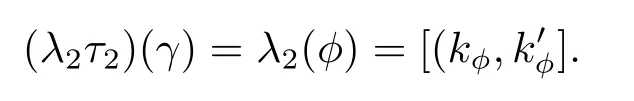
這里φ(l)=(πγt)(l),l∈L. 由于φ=τ2(γ),αl=αφ(l),由引理 3.3 的 (ii),(iv)及θ=γ|A=idA,可知,
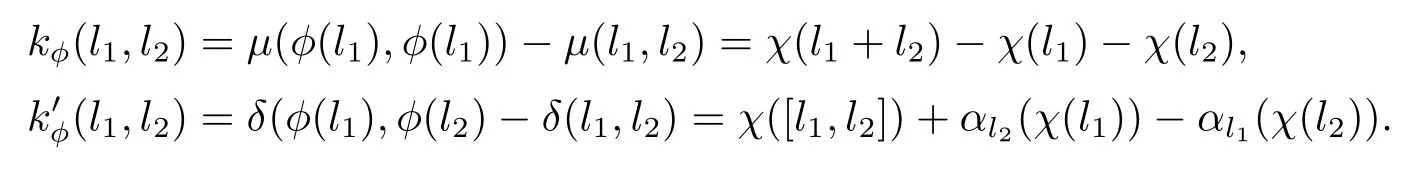
因?yàn)棣谩蔄utA(E),因此故Im(τ2)?Ker(λ2).
下面證明Ker(λ2)?Im(τ2).設(shè)φ∈Ker(λ2),則存在一個(gè)映射χ:L→A滿足λ(0)=0.使得,
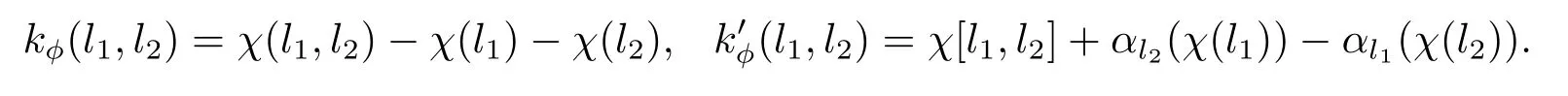
由引理3.3,令θ=id|A,則?l∈L,?a∈A,有一個(gè)自同構(gòu)γ∈AutA(E)滿足
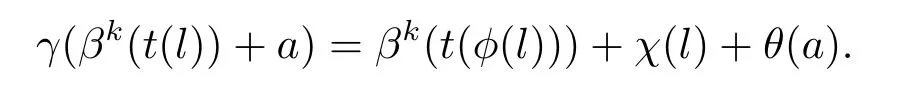
因此有γ(a)=θ(a)=a,γ∈AutA(E),且顯然有τ2(γ)=φ. 故 Ker(λ2)?Im(τ2).證畢.
引理3.11令是阿貝爾擴(kuò)張且θ∈C1,φ∈C2,定義
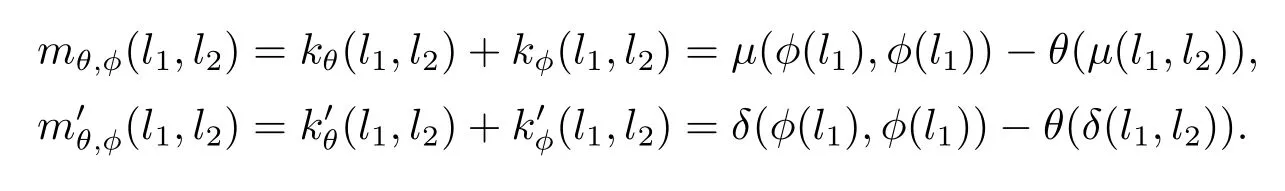
證由引理定義可知,要證只需證明以下兩式成立即可:
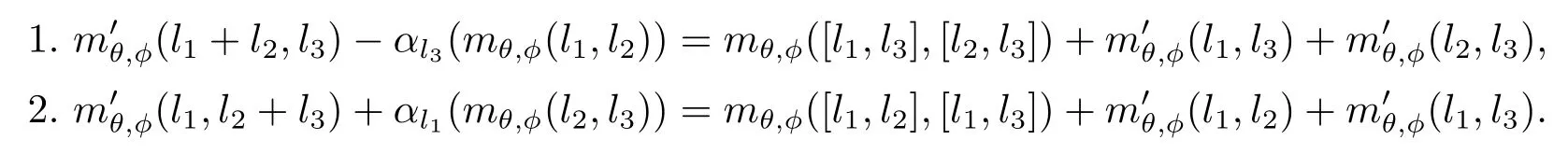
由
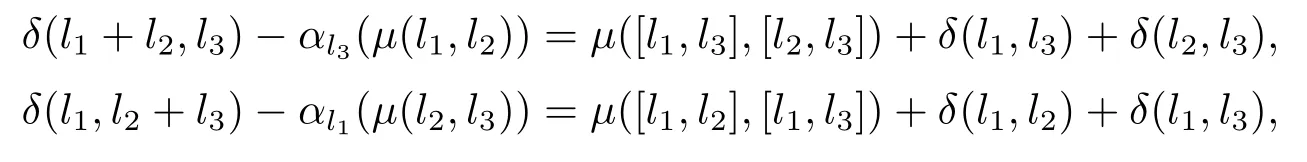
及等式
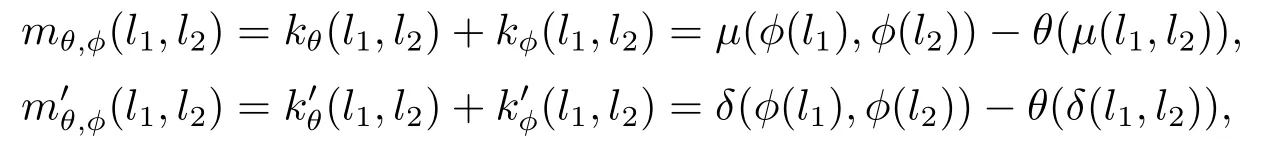
可知
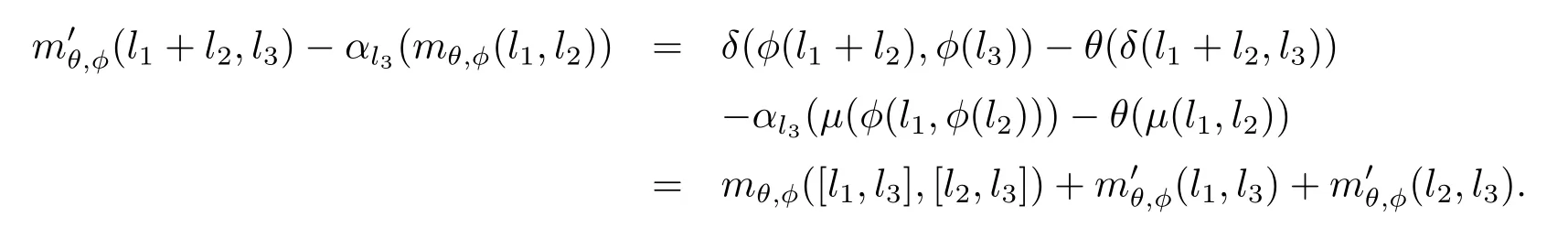
同理可證
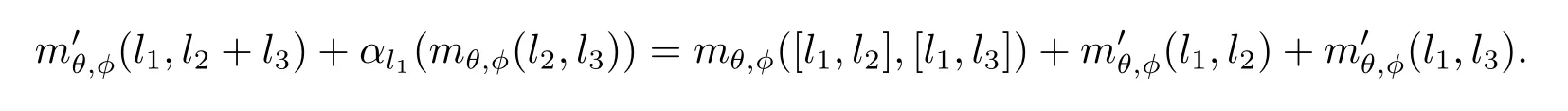
定理3.12令A(yù)→E?→πL是一個(gè)中心擴(kuò)張,則存在下列正合序列:
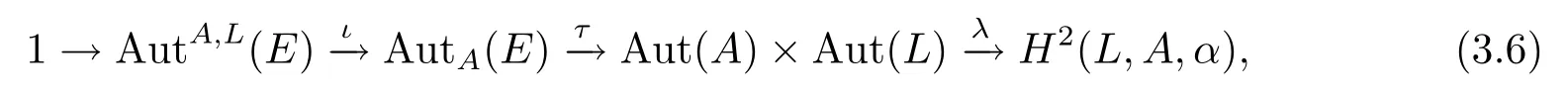
證在AutA,L(E)和AutA(E)上序列顯然是正合的.在證明此定理之前,可以證明λ是定義明確的.若(θ,φ)∈Aut(A)×Aut(L)是由γ∈AutA(E)所誘導(dǎo)的,則通過引理3.5的(ii)和(iii)存在一個(gè)映射χ:L→A滿足λ(0)=0使得
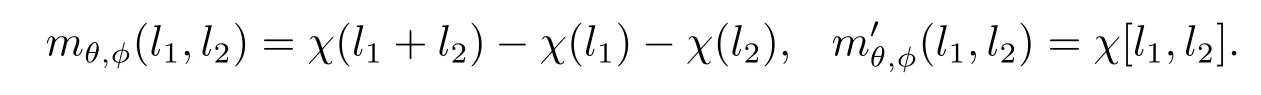
相反的, 如果 (θ,φ)∈Aut(A)×Aut(L) 滿足則存在一個(gè)映射χ:L→A滿足λ(0)=0使得
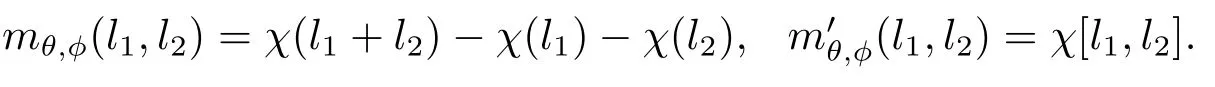
現(xiàn)由引理3.6知存在一個(gè)自同構(gòu)γ∈AutA(E)使得τ(γ)=(θ,φ).證畢.
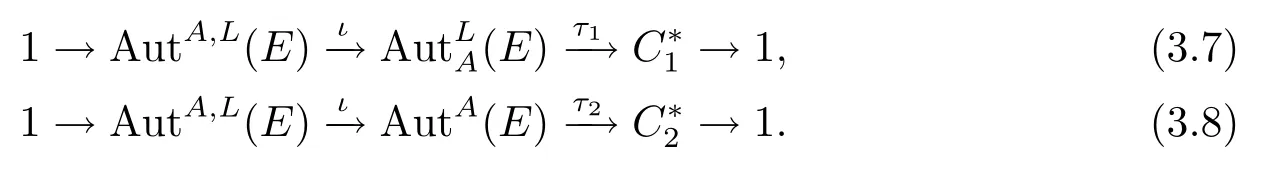
接下來,將證明如果原正合序列可裂,則這兩個(gè)正和序列也是可裂的.
定理3.13令E是一個(gè)hom-李環(huán),且A是E的一個(gè)阿貝爾理想,如果序列A→E→L分裂,則序列(3.7),(3.8)也可裂.
證在中存在一個(gè)hom-李環(huán)同態(tài)t:L→E滿足π?t=idL,而且對E中的每個(gè)元素都可以唯一的用βk(t(l))+a表示出來,其中l(wèi)∈L;a∈A.首先證明(3.7)可裂.
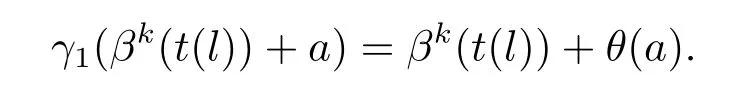
對任意的x1=βk(t(l1))+a1,x2=βk(t(l2))+a2,由于t是同構(gòu)映射,則有
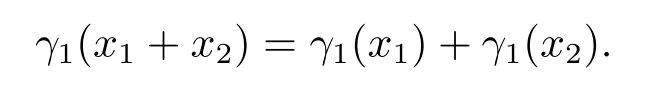
又由于θ∈C1,有,
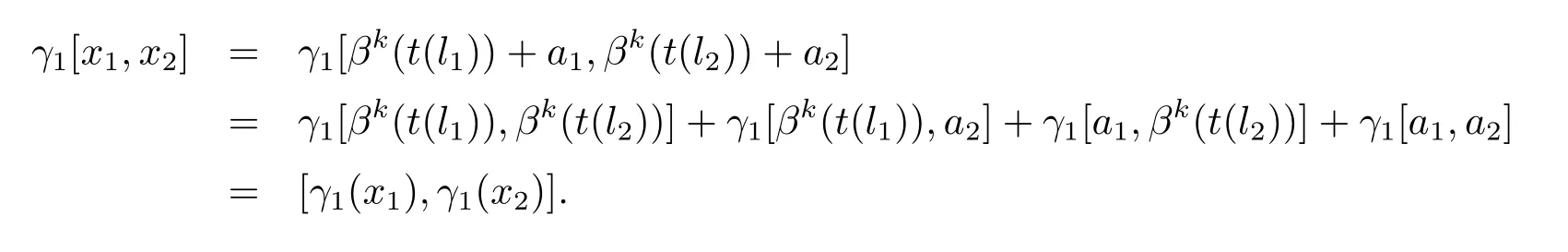
又由于γ1β=βγ1,這就證明了γ1是hom-李環(huán)同態(tài).顯然可知:是群同態(tài)且所以序列(3.7)可裂.
現(xiàn)在證明(3.8)可裂.定義一個(gè)映射ψ2:C2?→AutA(E)使得其滿足ψ2(φ)=γ2,這里γ2:E→E,滿足運(yùn)算
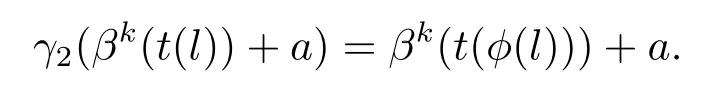
對任意的x1=βk(t(l1))+a1,x2=βk(t(l2))+a2∈E,由于t是同構(gòu)映射,有,
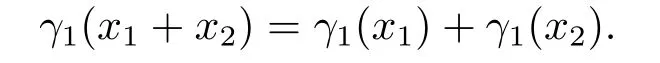
又由于φ∈C2,有αl=αφ(l),?l∈L.故
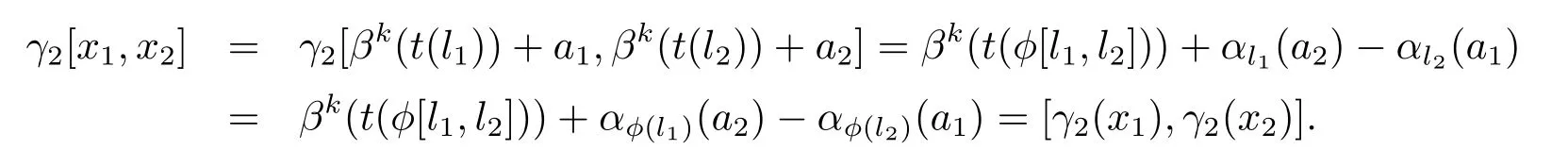
又由于γ2β=βγ2,這就證明了γ2是hom-李環(huán)的自同構(gòu),顯然可知:γ2∈AutA(E),γ2是群自同構(gòu)且τ2?ψ2=idC2?.所以序列(3.8)可裂.證畢.
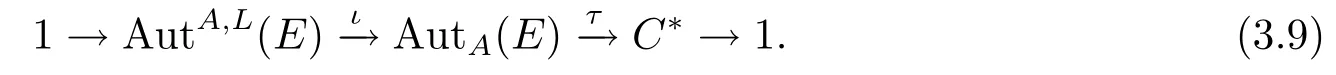
接下來,將證明如果原始的正合序列可裂,則這個(gè)正和序列也是可裂的.
定理3.14令E是一個(gè)hom-李環(huán),且A是E的一個(gè)阿貝爾理想,進(jìn)一步,若A?Z(E),如果序列A→E→L分裂,則序列(3.9)也可裂.
證在中存在一個(gè)hom-李環(huán)同態(tài)t:L→E,滿足π?t=idl,而且對E中的每個(gè)元素都可以唯一的用βk(t(l))+a表示出來,其中l(wèi)∈L,a∈A.現(xiàn)在證明(3.9)可裂.
由ψ(θ,φ)=γ定義一個(gè)映射ψ:C?→AutA(E),這里γ:E→E,滿足運(yùn)算
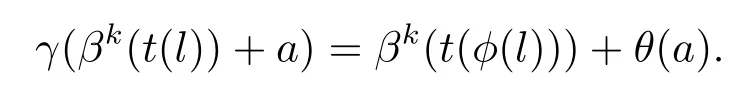
對任意的x1=βk(t(l1))+a1,x2=βk(t(l2))+a2∈E,有γ(x1+x2)=γ(x1)+γ(x2).由于t是自同態(tài)映射,且A?Z(E).可知,

又由于γβ=βγ,故γ是自同態(tài).不難得知γ∈AutA(E),ψ是群同態(tài),且τ?ψ=idC?.所以序列(3.9)可裂.證畢.
4 相關(guān)應(yīng)用
本節(jié),在定理3.10(3.4)的基礎(chǔ)上,將Z(E)的自同構(gòu)推廣到E的自同構(gòu).以下引理顯然成立.
引理4.1令E是一個(gè)hom-李環(huán).
(1)若E是阿貝爾hom-李環(huán),則E的任何加法子群也都是E的子環(huán).
(2)若E是不含有非平凡子環(huán)的平凡hom-李環(huán),則E是素?cái)?shù)階循環(huán)的.
引理4.2令M是hom-李環(huán)E的子環(huán),取?E(M)={x∈E|[x,M]?M},則以下結(jié)論成立.
(i)?E(M)是hom-李環(huán)E的子環(huán),且M??E(M).
(ii)M是E的一個(gè)理想當(dāng)且僅當(dāng)?E(M)=E.
(iii)[K,M]?M當(dāng)且僅當(dāng)K??E(M),這里K是E的子環(huán).
(iv)若E是冪零的且M?E,則M??E(M).
(v)若E是冪零的,且M是E的最大子環(huán),則M是E理想且E/M是素?cái)?shù)階.
引理4.3令E是hom-李環(huán),以下結(jié)論成立.
(i)若E是有限維的,則Φ(E)恰好由E的所有非生成元組成.
(ii)E/I是阿貝爾的當(dāng)且僅當(dāng)E0?I.
(iii)若E是冪零的,則E0?Φ(E).
(iv)若E是冪零的,則Φ(E)是E的理想.
(v)若E是冪零的且非平凡,則Z(E)0.
定理4.4令E是一個(gè)階為pn(p≥2)的hom-李P環(huán),Z(E)是循環(huán)的且Φ(E)?Z(E).則每一個(gè)Z(E)的p自同構(gòu)都可以被擴(kuò)張成依賴于的E上的自同構(gòu),這里,A=Z(E),L=E/Z(E).
證令A(yù)=hxi,|A|=pω,且π:E→L是自然同態(tài).所以得到一個(gè)中心擴(kuò)張A→E→L.容易看出每一個(gè)A上的每一個(gè)循環(huán)群都保留著李乘.現(xiàn)在由第二章的注記得到C1=Aut(A)~=ZPω?1(P?1).注意到θ=γ|A. 因?yàn)橛笑?l)=(πγt)(l)=l.所以擴(kuò)張是中心擴(kuò)張.定義θ:A→A滿足θ(x)=mx,這里m=1+jp且1≤m 由pt(l)∈pE?Φ(E)?A且p整除1?m,可以定義映射χ:L→A使得其滿足χ(l)=(1?m)t(l).因此, 同樣的,對?a,b∈E,有p[a,b]=0.故pE?Φ(E)?A.因此,
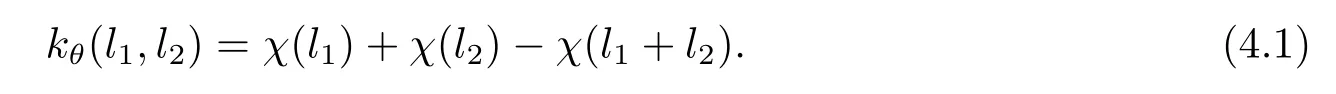
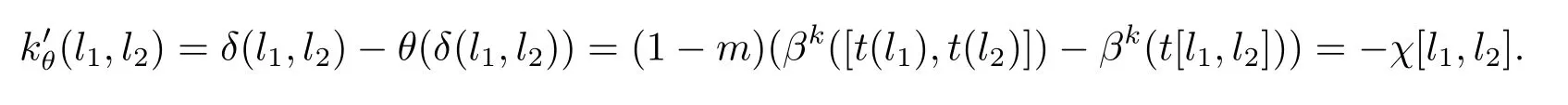
- 數(shù)學(xué)雜志的其它文章
- RESEARCH ANNOUNCEMENTS ON“MAXIMAL ERGODIC INEQUALITIES FOR SOME POSITIVE OPERATORS ON NONCOMMUTATIVE LP-SPACE”
- SYNCHRONIZATION OF COMPLEX NETWORKS VIA A SIMPLE AND ECONOMICAL FIXED-TIME CONTROLLER
- DIFFERENCE HARNACK ESTIMATES FOR WEIGHTED NONLINEAR REACTION-DIFFUSION EQUATIONS ON WEIGHTED RIEMANNIAN MANIFOLDS
- 在CEV模型下帶違約風(fēng)險(xiǎn)的時(shí)間一致再保險(xiǎn)投資博弈
- 環(huán)上含參變量的Boltzmann測度的對數(shù)Sobolev不等式
- Schrdinger-Virasoro代數(shù)上的Poisson結(jié)構(gòu)

