環(huán)上含參變量的Boltzmann測度的對數(shù)Sobolev不等式
程 新,毛 閏,張正良
(1.武漢大學數(shù)學與統(tǒng)計學院,武漢 430072)
(2.重慶市第八中學校,重慶 401120)
1 引言
Poincaré不等式,傳輸不等式和對數(shù)Sobolev不等式是研究測度集中性的有力工具[1,2].在這三類不等式中,對數(shù)Sobolev不等式強于Talagrand傳輸不等式,Talagrand傳輸不等式不等式又強于Poincaré不等式,具體例子可分別參看文獻[3,4].在文獻[5]中,Qian,Ma,Zhang證明了Boltzmann測度在維數(shù)n≥3固定時關于參數(shù)h>0滿足一致的對數(shù)Sobolev不等式,但是并沒有討論n=2的情形.在Ma與Zhang的文獻[6]中,作者針對n=2的情形給出了Boltzmann測度比較精確的譜系,而且有趣的是:當h→∞時,譜系以h的速率趨于無窮大,即龐加萊常數(shù)以1/h的速率趨于0.本文將給出在n=2時,對數(shù)Sobolev常數(shù)CLS(μh)關于h>0的一致非0上下界,這在一定程度上也能表明三個不等式之間的強弱關系.下面先介紹一下Boltzmann測度以及相關不等式.
Boltzmann測度設Sn?1是Rn(n≥2)上的單位球面,μ是Sn?1上的標準Lebesgue測度,i.e.μ=σn?1/sn?1,其中σn?1為單位球面Sn?1上的均勻測度,sn?1:=nπn/2/Γ(1+n/2)為單位球面面積(歸一化因子).對任意的h>0和e1=(1,0,...,0)∈Sn?1,單位球面Sn?1上的概率測度μh有如下表達式:
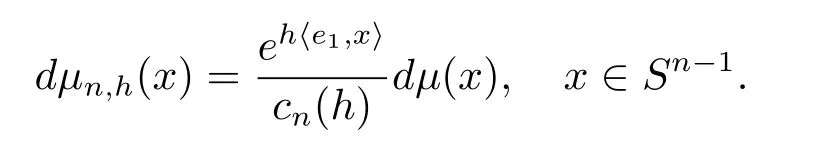
其中,cn(h)為歸一化因子.稱該概率測度μh為外磁場下的Boltzmann測度.特別n=2時,S1即為環(huán),我們簡記為S,對應測度μ2,h簡記為μh,此即為本文所考慮的含參變量h的環(huán)上的Boltzmann測度.
下面介紹幾個相關不等式:設M是一個完備黎曼流形,其上的測地度量記為d,?為M上的梯度.M1(M)為M上的概率測度空間.
Poincar不等式我們稱測度μ∈M1(M)滿足 Poincar不等式(記μ∈PI(C)),若對任意光滑函數(shù)f:M→R,都存在非負常數(shù)C使得
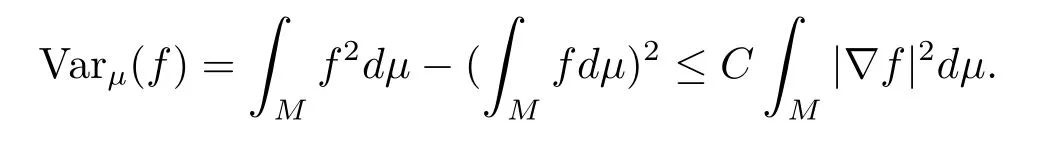
記CP(μ) 為最佳 Poincar常數(shù).
Lp傳輸不等式稱測度μ滿足Lp傳輸不等式,若對任意的ν=f2μ∈M1(M),都存在非負常數(shù)C使得
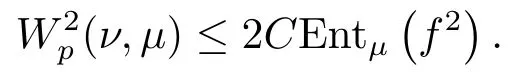
其中Wp(ν,μ)是測度ν和μ的Lp-Wasserstein距離,其定義如下:
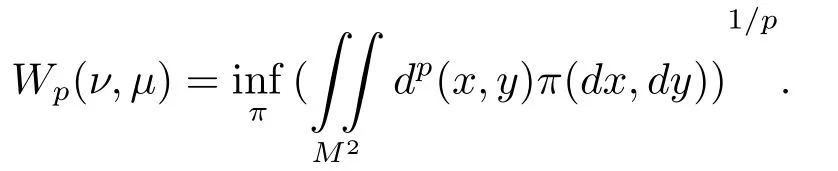
這里π是M×M上的概率測度,其邊緣分布為μ,ν.記CWpH(μ)為滿足該不等式的最佳常數(shù).
對數(shù)Sobolev不等式稱測度μ滿足對數(shù)Sobolev不等式,若對任意光滑函數(shù)f:M→R,都存在非負常數(shù)C使得
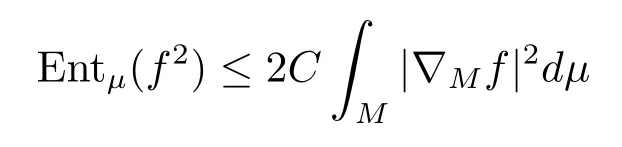
成立,其中Entμ(f2):=μ(f2logf2)?μ(f2)log(μ(f2))為函數(shù)f2關于μ的熵.記CLS(μ)為最佳對數(shù)Sobolev常數(shù).
2 準備工作
本文沿用[7,8]中的降維方法:設νh為μh在映射x→d(e1,x)下的像測度,則νh為[0,π]上的概率測度,其概率密度為為歸一化因子.
在處理環(huán)上測度的對數(shù)Sobolev不等式時可參考如下的降維定理.
定理2.1[8]設μ為環(huán)S上的均勻測度,M為S上的概率測度,其定義如下
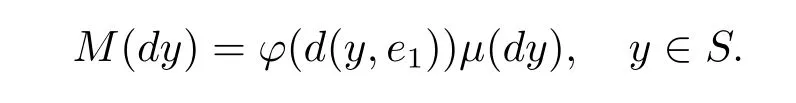
其中,?是非負可測的.設M在映射y→d(y,e1)下的像測度為ν,則最佳對數(shù)Sobolev常數(shù)滿足其中,λDD(ν) 是滿足 [0,π]上 Dirichlet 邊界條件的ν的第一特征值.
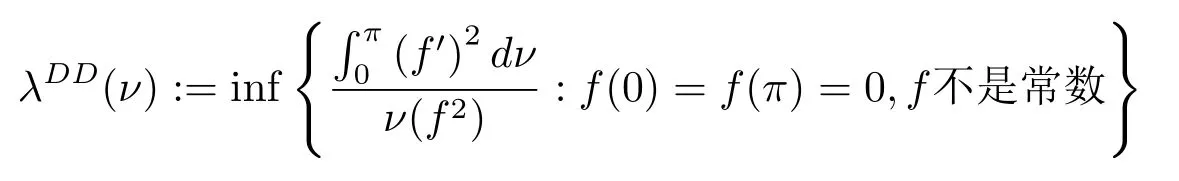
而對于本文中所考慮的Boltzmann測度對應的λDD(νh)也有如下估計.
引理2.2[6]對于任意h>0,對任意的光滑函數(shù)f:S→R,νh為Boltzmann測度μh在映射x→d(e1,x)下的像測度,則Dirichlet邊界條件下的第一特征值λDD(νh)滿足
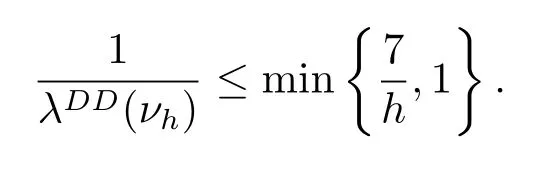
在上面兩個結論的基礎上,本文的討論將主要集中在[0,π]上的一維測度νh上.針對一維測度,Barthe和Roberto在[9]中給出了關于對數(shù)Sobolev不等式的刻畫,現(xiàn)陳述如下.
定理2.3[9]設μB,νB是R 上的Borel測度,其中μB(R)=1且dνB(x)=n(x)dx,n(x)為一絕對光滑函數(shù).設m是測度μB上的中位數(shù),且對任意光滑函數(shù)f:R→R,滿足
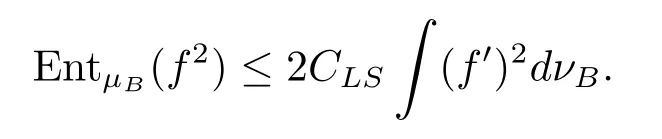
其中,CLS為最佳對數(shù)Sobolev常數(shù).則有max(b?,b+)≤2CLS≤4max(B?,B+),其中
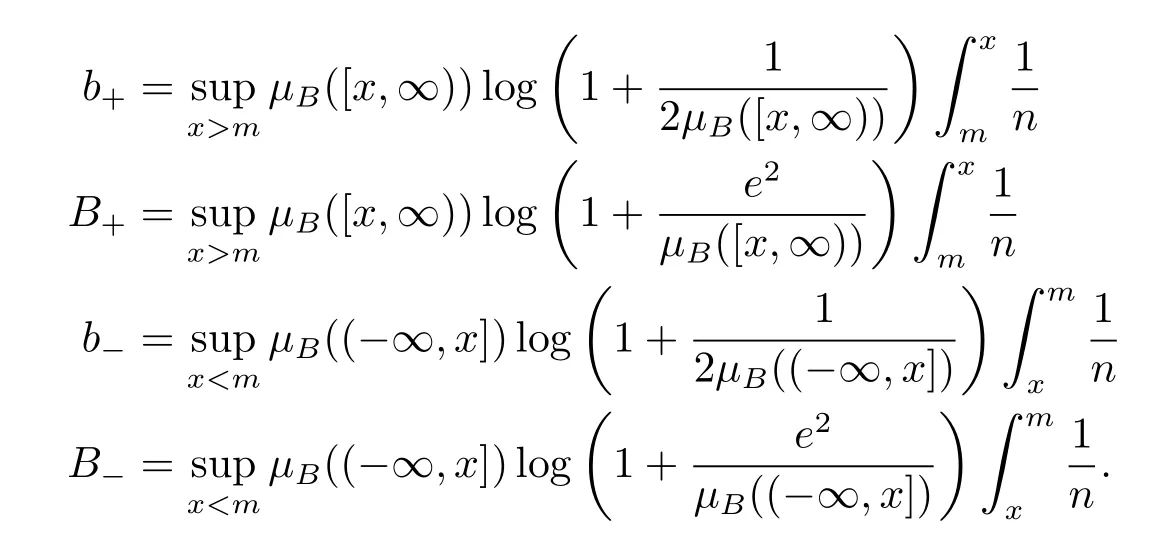
注意到,對于任意0≤y≤1/2,都有因此,B+≤4b+且B?≤4b?.不難發(fā)現(xiàn),此時最佳對數(shù)Sobolev常數(shù)CLS滿足max(b?,b+)≤2CLS≤16max(b?,b+).本文的目的僅在于給出常數(shù)階,故此證明也只需去估計b?,b+.為此還需下面幾個估計.
引理2.4設則
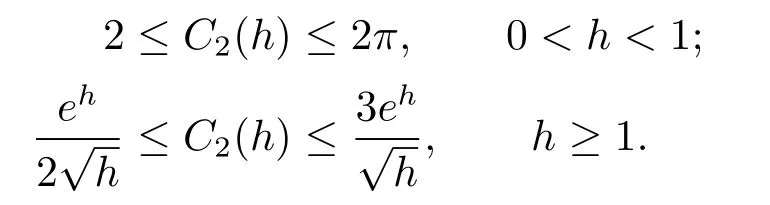


3 主要結論
定理3.1對于任意h>0,νh為Boltzmann測度μh在映射x→d(e1,x)下的像測度,則νh滿足一致的對數(shù)Sobolev不等式,即對于任意光滑函數(shù)f:S→R,有其中對數(shù)Sobolev最佳常數(shù)CLS(νh)一致有界,且滿足

進而有,環(huán)S上的Boltzmann測度μh滿足一致的對數(shù)Sobolev不等式,且最佳常數(shù)CLS(μh)滿足
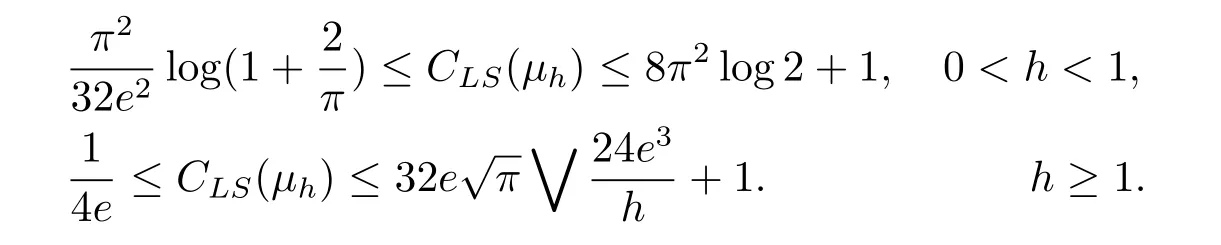
注從定理結論中我們可以看出,對于任意的h>0,CLS(μh)=O(1).而在[6]中,作者給出了該測度譜系的比較精確的刻畫此即說明 Poincaré常數(shù)CP(μh)=1/λ1(μh)=O(1/h),再通過[10]中的結論,我們還可知道Talagrand傳輸不等式常數(shù)此也可佐證對數(shù)Sobolev不等式嚴格強于Talagrand傳輸不等式.
4 定理3.1的證明
根據(jù)降維定理2.1,我們僅需考慮一維測度νh,再由定理2.3,考慮如下的b+,b?

討論將分兩種情形展開.
情形10 其次,考慮b+的上界.因對任意在x>0上都是單調遞增的,故有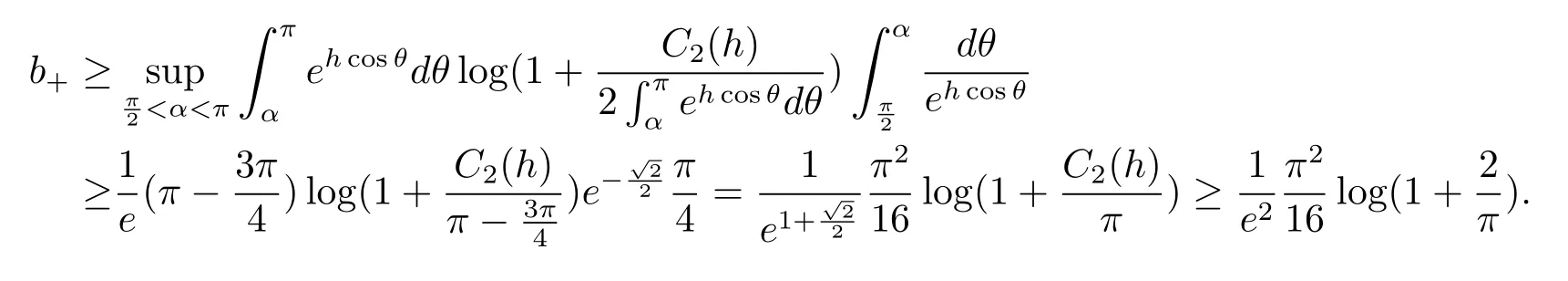
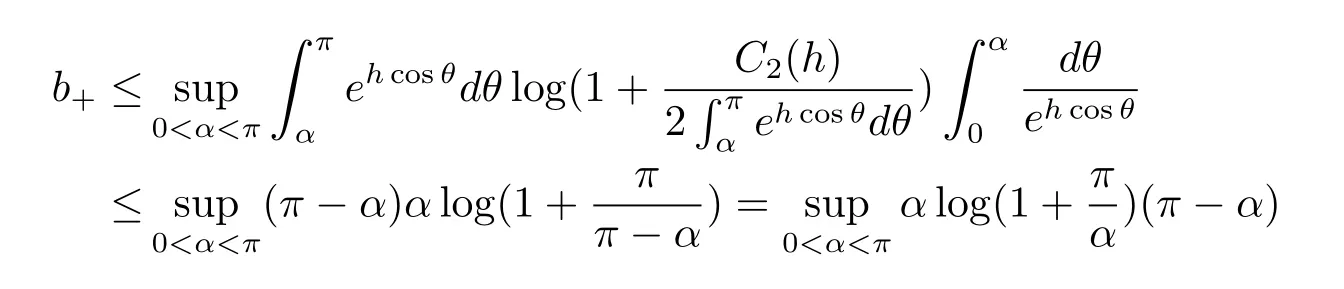



- 數(shù)學雜志的其它文章
- RESEARCH ANNOUNCEMENTS ON“MAXIMAL ERGODIC INEQUALITIES FOR SOME POSITIVE OPERATORS ON NONCOMMUTATIVE LP-SPACE”
- SYNCHRONIZATION OF COMPLEX NETWORKS VIA A SIMPLE AND ECONOMICAL FIXED-TIME CONTROLLER
- DIFFERENCE HARNACK ESTIMATES FOR WEIGHTED NONLINEAR REACTION-DIFFUSION EQUATIONS ON WEIGHTED RIEMANNIAN MANIFOLDS
- 在CEV模型下帶違約風險的時間一致再保險投資博弈
- 阿貝爾hom-李環(huán)擴張的自同構
- Schrdinger-Virasoro代數(shù)上的Poisson結構

