EXTINCTION OF A DISCRETE COMPETITIVE SYSTEM WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE AND THE EFFECT OF TOXIC SUBSTANCES??
Jiangbin Chen
(Zhicheng College,Fuzhou University,Fuzhou 350002,Fujian,PR China)
Shengbin Yu?
(Department of Basic Teaching and Research,Yango University,Fuzhou 350015,Fujian,PR China)
Abstract
Keywords discrete competitive system;Beddington-DeAngelis functional response;extinction;toxic substances
1 Introduction
In the paper,we are concerned with the extinction property of the following discrete competitive phytoplankton system with Beddington-DeAngelis functional response and the effect of toxic substances:
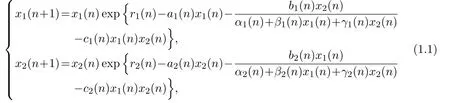
where x1(n),x2(n)are population densities of species x1and x2at the nth generation,respectively.ri(n)(i=1,2)are the intrinsic growth rates of species;ai(n)(i=1,2)are the rates of intraspecific competition of the first and second species;the interspecific competition between two species takes the Beddington-DeAngelis functional response type
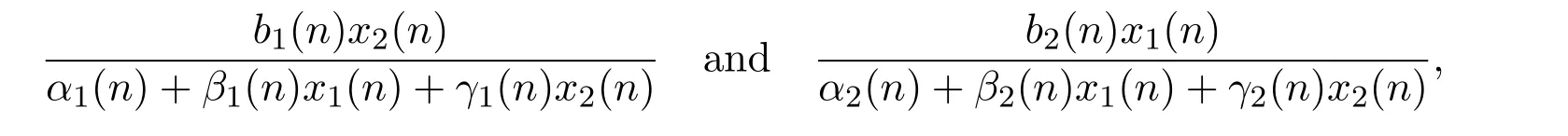
respectively.The terms ci(n)x1(n)x2(n)(i=1,2)denote the effect of toxic substances,under the assumption that each species produces a substance toxic to the other,only when the other is present.
We will also consider the extinction property of the following two species nonautonomous competitive phytoplankton system with Beddington-DeAngelis functional response:
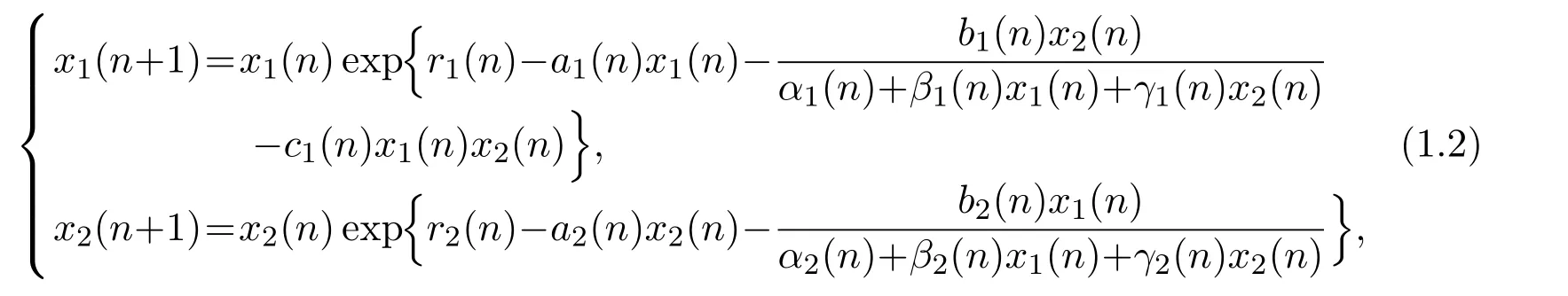
where all the coefficients have the same meaning as those of system(1.1).However,we assume that the second species could produce toxic,while the first one is nontoxic producing.
Motivated by Gopalsamy[1],Qin,Liu and Chen[2]studied the following discrete competitive system:
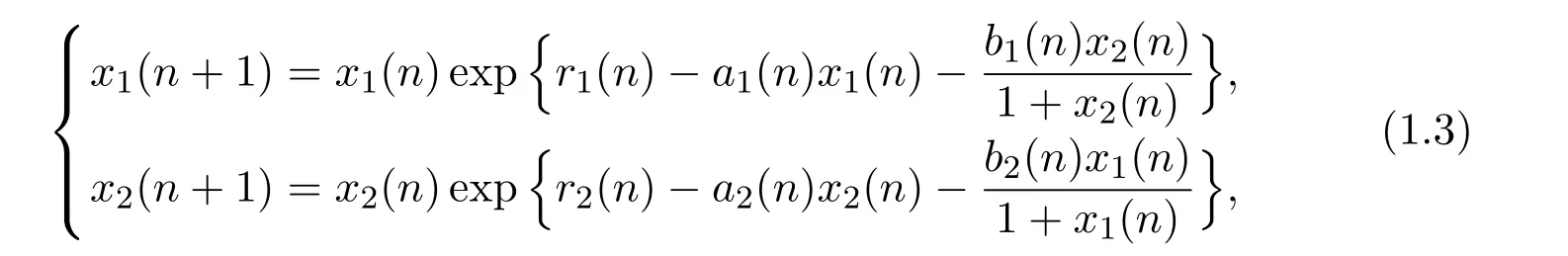
which is a special case of system(1.1)with αi(n)= γ1(n)= β2(n)=1 and β1(n)=γ2(n)=ci(n)=0(i=1,2).Qin et al.[2]obtained sufficient conditions on the permanence and global asymptotic stability of positive periodic solutions of system(1.3).Wang and Liu[3]further considered the existence,uniqueness and uniformly asymptotic stability of positive almost periodic solution of system(1.3)with almost periodic parameters.Extinction of a species and the stability property of another one were considered in[4].Noting that ecosystems in the real world are often distributed by unpredictable forces that can result in changes in biological parameters,Wang et al.[5]considered system(1.3)with feedback controls and established a criterion for the existence and uniformly asymptotic stability of unique positive almost periodic solution of the system.We[6,7]further showed the influence of feedback control variables on the persistent and extinction property of the system(1.3)with feedback controls.
In 2008,Li and Chen[8]studied the following discrete competitive system with the effect of toxic substances:
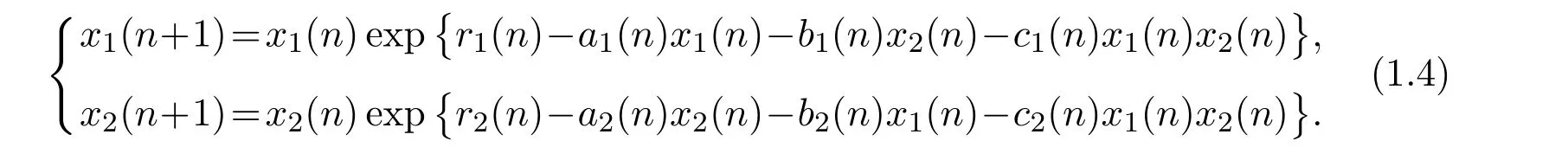
and got sufficient conditions which guarantee the extinction of a species and global attractivity of the other one.One can easily find that system(1.4)is a special case of system(1.1)with βi(n)= γi(n)=0 and αi(n)=1(i=1,2).Yue[9]further considered system(1.3)with the effect of toxic substance where species x2is toxic producing while x1is non-toxic producing.
Considering that Beddington-DeAngelis functional response performs better than Holling type II functional response,Chen,Chen and Huang[10]further proposed and studied the following two species non-autonomous competitive system with Beddington-DeAngelis functional response and the effect of toxic substances:

By constructing some suitable Lyapunov type extinction functions,sufficient conditions on the extinction of a species and global attractivity of the other one were obtained.
As is well known,when the size of the population is relatively small,the discrete time models governed by difference equations are more appropriate than the continuous ones.Stimulated by the above papers and reasons,we propose system(1.1)which is the discrete analogue of system(1.5)and investigate the extinction property of systems(1.1)and(1.2)in this paper.For more works in this direction,we refer to[11-22]and the references therein.

(H1){ri(n)}are bounded sequence defined on Z;{ai(n)},{bi(n)},{ci(n)},{αi(n)},{βi(n)}and{γi(n)}i=1,2 are non-negative sequences bounded above and below by positive constants.
(H2)There exists a positive integer ω such that for each i=1,2,
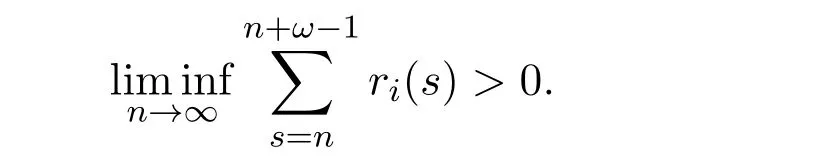
As regards the biological background,we will focus our discussion on the positive solutions of systems(1.1)and(1.2).So,we consider systems(1.1)and(1.2)together with the following initial conditions:

It is obvious that the solutions of systems(1.1)and(1.2)with initial conditions(1.6)are well defined and satisfy
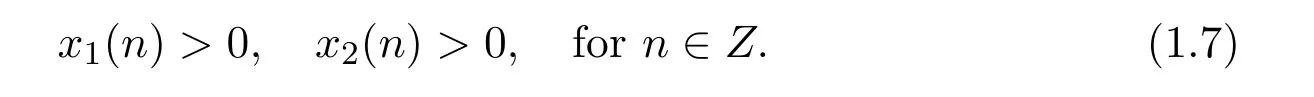
The rest of this paper is organized as follows.We study the the extinction of a species and the global attractivity of the other one in Sections 2 and 3.Some examples together with their numerical simulations are carried out to show the feasibility of our results in Section 4.We end this paper with a brief discussion.
2 Extinction of x2and Stability Property of x1
In this section,we will establish sufficient conditions on the extinction of species x2and the stability property of x1.By the similar proof of Lemma 2.1 in Li and Chen[8],we can obtain:








for all n≥n6.The following proof is exactly the same as the analysis of Theorem 2.1 and we omit the details here.This ends the proof of Theorem 2.4.
When αi(n)= γ1(n)= β2(n)=1 and β1(n)= γ2(n)=ci(n)=0(i=1,2),system(1.1)becomes system(1.3).According to Theorems 2.2-2.4,we can obtain the following corollary.
Corollary 2.2 In addition to(H1)-(H2),further suppose that:
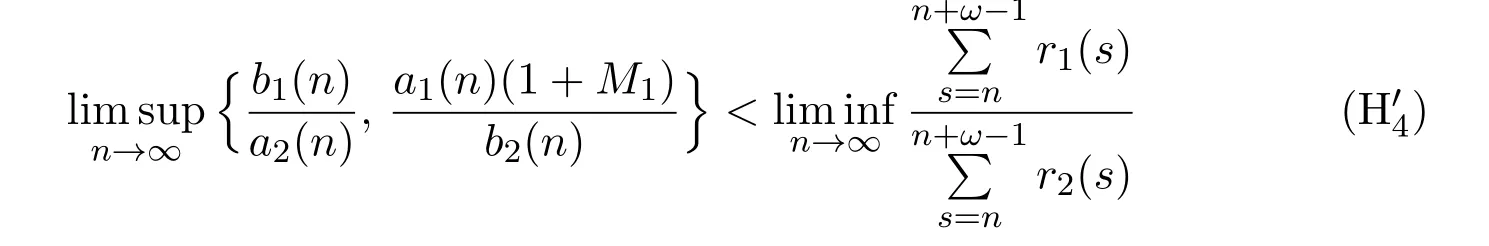
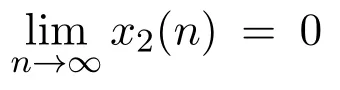
Remark 2.2 Since(H′4)is weaker than(H1)given in[4],our results improve and generalize the corresponding results in[4].
In the following part of this section,we will investigate the stability property of the first species x1under the extinction of second species x2.For simplicity,we always assume that r1(n)is non-negative sequences bounded above and below by positive constants.Let us first state several lemmas which will be useful in proving the main result of this section.

Lemma 2.3 Suppose conditions in Theorem 2.1 or 2.2 or 2.3 or 2.4 hold,let(x1(n),x2(n))Tbe any positive solution of system(1.1),then


A1?ε≤ x1(n)≤ M1+ε6, x2(n)≤ ε6, A1?ε≤ x(n)≤ M1+ε6. (2.47)Note that θ(n) ∈ (0,1)implies that x(n)exp(θ(n)y(n))lies between x(n)and x1(n).From(2.45)and(2.47),for n≥n8,one can get

3 Extinction of x1and Stability Property of x2
Similarly to the proofs of Theorems 2.1-2.5,one could easily establish the following parallel results as those of Theorems 2.1-2.5 for the extinction of species x1and the stability property of species x2.We omit the detailed proofs here.


4 Examples and Numeric Simulation
In this section,we give the following examples to show the feasibilities of our results.For simplicity,our examples just show results on the extinction of species x2and the stability property of species x1,since the other case can be similarly verified.

Since max{0.06,0.5,0.1397}<2.4,(4.2)-(4.5)show that condition(H3)is satisfied and hence all the conditions of Theorem 2.1 are satisfied.Moreover,
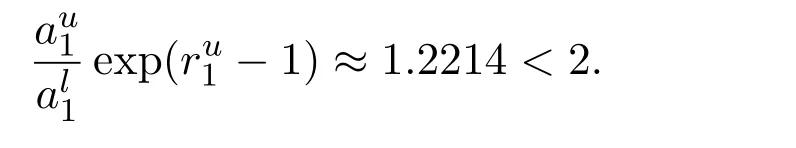
Hence,condition(H7)is also satisfied.It follows from Theorem 2.5 that the second species in system(4.1)will be driven to extinction and the first species is globally attractive.Numeric simulations(Figure 1)also support this result.
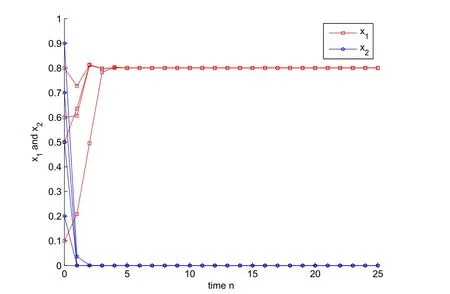
Figure 1:Dynamic behaviors of system(4.1)with the initial condition(x1(0),x2(0))=(0.5,0.5)T,(0.8,0.2)T,(0.1,0.9)Tand(0.6,0.7)T,respectively.


Hence,condition(H7)is also satisfied.It follows from Theorem 2.5 that the second species in system(4.6)will be driven to extinction and the first species is globally attractive.Numeric simulations(Figure 2)also support this result.
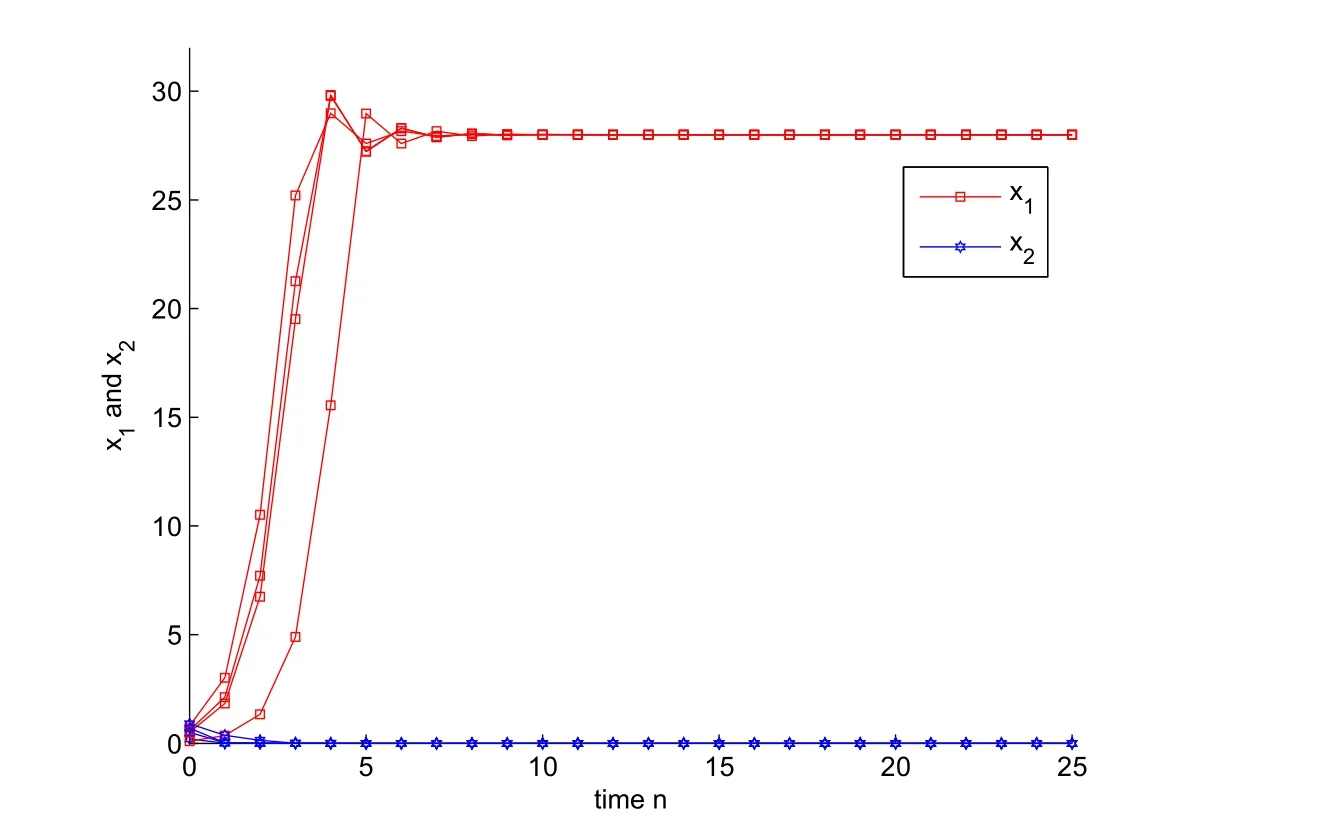
Figure 2:Dynamic behaviors of system(4.6)with the initial condition(x1(0),x2(0))=(0.5,0.5)T,(0.8,0.2)T,(0.1,0.9)Tand(0.6,0.7)T,respectively.



Figure 3:Dynamic behaviors of system(4.10)with the initial condition(x1(0),x2(0))=(0.5,0.5)T,(0.8,0.2)T,(0.1,0.9)Tand(0.6,0.7)T,respectively.

and

Since max{1.5792,1.6844}<2,(4.14)-(4.15)show that condition(H6)is satisfied and hence all the conditions of Theorem 2.4 are satisfied.Moreover,
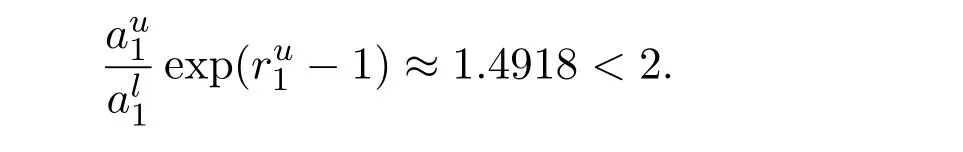
Hence,condition(H7)is also satisfied.It follows from Theorem 2.5 that the second species in system(4.13)will be driven to extinction and the first species is globally attractive.Numeric simulations(Figure 4)also support this result.
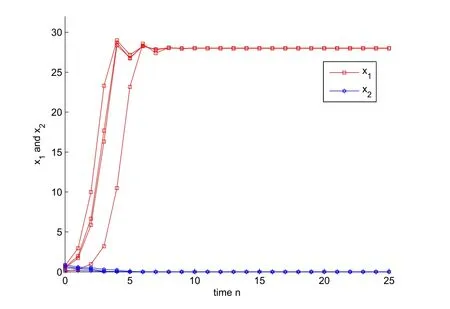
Figure 4:Dynamic behaviors of system(4.13)with the initial condition(x1(0),x2(0))=(0.5,0.5)T,(0.8,0.2)T,(0.1,0.9)Tand(0.6,0.7)T,respectively.
5 Discussion
In this paper,we consider a discrete competitive system with Beddington-DeAngelis functional response.By constructing some suitable Lyapunov type extinction functions,sufficient conditions which guarantee the extinction of a species and global attractivity of the other one are obtained.When αi(n)= γ1(n)= β2(n)=1 and β1(n)= γ2(n)=ci(n)=0(i=1,2),system(1.1)becomes system(1.3)discussed in[2-4].Conditions in Corollaries 2.2 and 3.3 are weaker than those in Theorem 1 and 2 given in[4],thus our results improve and generalize the corresponding results in[4].If βi(n)= γi(n)=0 and αi(n)=1(i=1,2),then system(1.1)becomes system(1.4)discussed by Li and Chen[8].Because conditions in Corollary 2.1 are weaker than those in Theorem 2.1 in[8]and Corollary 3.2 shows the extinction of species x1which is not considered in Li and Chen[8],thus our results improve,supplement and generalize the corresponding results in[8].Moreover,since system(1.1)is a continuous analogue of system(1.5),our results also supplement those in Chen,Chen and Huang[10].To sum up,our results not only supplement and improve but also generalize some existing ones.
 Annals of Applied Mathematics2020年4期
Annals of Applied Mathematics2020年4期
- Annals of Applied Mathematics的其它文章
- INVERSE SCATTERING METHOD AND APPLICATIONS?
- THE GENERALIZED JACOBIAN OF THE PROJECTION ONTO THE INTERSECTION OF A HALF-SPACE AND A VARIABLE BOX?
- EXISTENCE OF UNBOUNDED SOLUTIONS FOR A n-TH ORDER BVPS WITH A p-LAPLACIAN??
- BASIC THEORY OF GENERALIZED p-TYPE RETARDED FUNCTIONAL DIFFERENTIAL EQUATIONS?
- OSCILLATION OF THIRD-ORDER NONLINEAR DELAY DIFFERENTIAL EQUATIONS??
- EULER APPROXIMATION FOR NONAUTONOMOUS MIXED STOCHASTIC DIFFERENTIAL EQUATIONS IN BESOV NORM??
