Sheng Fang

(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,Fujian,PR China)

Yong-Jin Liu?

(Key Laboratory of Operations Research and Control of Universities in Fujian,College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,Fujian,PR China)

Abstract

Keywords generalized HS Jacobian;projection;intersection of a halfspace and a variable box

1 Introduction

Given(x,t)∈?n×? and r＞0,we consider the following optimization problem:

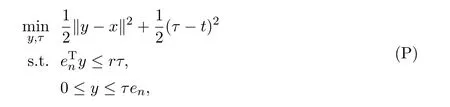
where endenotes the vector of all ones in ?n.For simplicity,we define Bras the intersection of a closed half-space and a variable box:

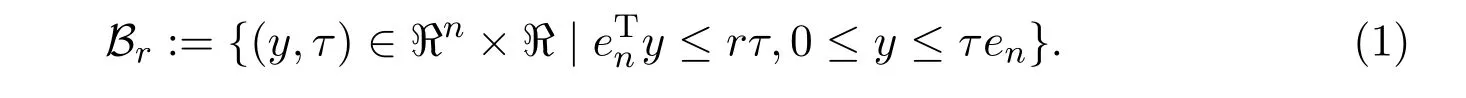
It is obvious(cf.[13])that Bris a polyhedral convex set.It is also easy to see that the optimal solution to(P)is the projection ΠBr(x,t)of(x,t)onto Br.

Fast solvers for computing the projection ΠBr(·,·)and the explicit formulas of the generalized Jacobian for ΠBr(·,·)are needed in designing efficient algorithms such as augmented Lagrangian methods for the optimization problems subject to the epigraph of the vector k-norm functions and the matrix Ky Fan k-norm functions.It is worth mentioning that Ky Fan k-norm functions appear frequently in matrix optimization problems.For instance,the problem of finding the fastest Markov chain on a graph which can be recast as minimizing the Ky Fan 2-norm was studied in[1,2].Besides,the structured low rank matrix approximation[3]arising in many areas is a kind of matrix optimization problem involving Ky Fan k-norm.For more applications,we refer the reader to[4,14]and references therein.

Note that the explicit formulas of the projection ΠBr(·,·)and the fast algorithm proposed for finding the projection ΠBr(·,·)were studied in[12],we mainly focus on the computation of the generalized Jacobian of ΠBr(·,·)in this paper.The generalized Jacobian of the projector ΠBr(·,·)plays an essential role in the algorithmic design of the second order nonsmooth methods for solving optimization problems with constraints involving Br.The efficiency and robustness of the algorithms which utilize the second order information like the semismooth Newton augmented Lagrangian methods(SSNAL)for solving the optimization problems have been demonstrated in many works[8–11,15].Thus,the efficient computation of generalized Jacobian of the metric projector ΠBr(·,·)deserves our research efforts.

As far as we know,the generalized Jacobian of the projection ΠBr(·,·)has not been studied before.The main contribution of this paper is to study the explicit formulas of the generalized HS-Jacobian[7,10]for the projection ΠBr(·,·).Due to the difficulty of characterizing the B-subdifferential and the Clarke generalized Jacobian of the projection onto the nonempty polyhedral convex set,Han and Sun[7]proposed a particular multi-valued mapping(HS-Jacobian)as an alternative for the generalized Jacobian of the projector onto polyhedral sets.Recently,the authors[10]derived an explicit formula for constructing the generalized HS-Jacobian and thus the computation of the generalized Jacobian was further simplified.Based on their works,we are able to study the generalized HS-Jacobian of ΠBr(·,·)in an efficient way.

The remaining parts of this paper are organized as follows.Section 2 reviews some preliminary results on the generalized Jacobian of the projection onto the general polyhedral convex set.This lays the foundation for the study on the generalized HS-Jacobian of the projection ΠBr(·,·)in Section 3.Finally,we conclude the paper in Section 4.

Notation For any positive integer p,we use Ipand epto denote the p×p identity matrix and the p-vector of all ones respectively.We denote the p×q zero matrix by 0p×qand p,q will be dropped from 0p×qwhen the dimension is clear from the context.Similarly,Ep×qdenotes the p×q matrix of all ones and is abbreviated as Epwhen p=q.The symbol spKrefers to the p-vector whose i-th component is 1 if i∈K and 0 otherwise.For any given vector z∈?p,Diag(z)denotes the p×p diagonal matrix whose diagonal is given by z.The notation A?is used to denote the Moore-Penrose inverse of given matrix A.

2 Generalized Jacobians of the Projection onto Polyhedral Convex Sets

where supp(?)is the support of ?,that is,the set of indices such that ?i?=0,and BKdenotes the submatrix of B with rows indexed by K.Due to the existence of the extreme point of M(z),we knows from[7]that the set KD(z)is nonempty.

For given z ∈ Rm,considering the difficulty of computing the B-subdifferential?BΠD(z)or the Clarke generalized Jacobian ?ΠD(z),we define the following multifunction P:?m??m×mcalled HS-Jacobian[7]as an alternative for?BΠD(z):

3 The HS Jacobian of the Projection ΠBr(·,·)

In this section,we shall study the generalized HS Jacobian of the projection onto the intersection of a closed half-space and a variable box.

For given(x,t)∈ ?n×?,let(y?,τ?):= ΠBr(x,t).Define the index sets associated with(y?,τ?)by

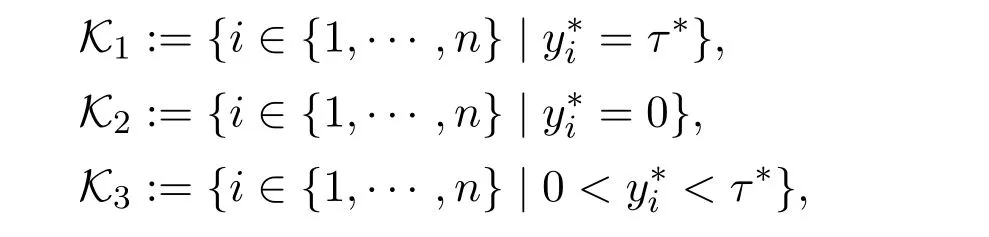
with cardinalities k1,k2and k3respectively.When τ??=0,we have

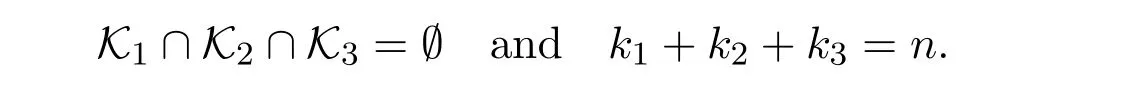
We also denote the submatrices of Inwith the rows in K1and K2by IK1and IK2respectively.

Theorem 3.1 Assume that r＞0 and(x,t)∈?n×? in(P)are given.Then,the optimal solution ΠBr(x,t)denoted as(y?,τ?)of(P)is unique and admits a closed-form expression.Moreover,the element N0of the generalized HS-Jacobian for ΠBr(·,·)at(x,t)has the following form:

4 Conclusion

In this paper,we study the generalized Jacobian for the projection of a vector onto the intersection of a closed half-space and a variable box.We derive the explicit formulas of an element in the set of the generalized HS Jacobian for the projection,which can be expressed as the combination of a diagonal matrix and few rank-one symmetric matrices.The explicit formulas of the HS Jacobian we obtained not only lay foundation for the algorithmic design of the second order nonsmooth methods,but also show that the computational cost would be cheap when the second order information are incorporated in the algorithms for the related optimization problems.We leave it as our future work.