EULER APPROXIMATION FOR NONAUTONOMOUS MIXED STOCHASTIC DIFFERENTIAL EQUATIONS IN BESOV NORM??
Sihui Yu,Weiguo Liu
(School of Statistics and Mathematics,Guangdong University of Finance&Economics,Guangzhou 510320,Guangdong,PR China)
Abstract
Keywords Brownian motion;fractional Brownian motion;Euler approximation;rate of convergence;Besov norm
1 Introduction
Consider a mixed stochastic differential equation(SDE)involving standard Brownian motion and fractional Brownian motion(fBm)with Hurst index H∈(1/2,1),both defined on the stochastic basis(?,F,{Ft}0≤t≤T,P),for t∈ [0,T],
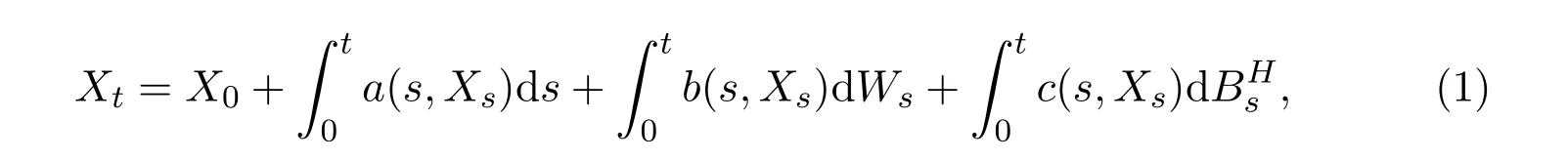
where X0is an F0-measurable random variable,E|X0|2<∞,the stochastic integral with respect to standard Brownian motion{Wt}t∈[0,T]and fBm{BHt}t∈[0,T]are interpreted as It?o and pathwise Riemann-Stieltjes integral respectively.Assumptions on the coefficients will be given in Section 3.
Since the seminal paper[2],mixed stochastic models containing both a standard Brownian motion and an fBm gained a lot of attention,see[3,4,8,10,11,15,16],and so on.They allow us to model systems driven by a combination of random noises,one of which is white and another has a long memory.The motivation to consider such equations comes from some financial applications,where Brownian motion as a model is inappropriate because of the lack of memory,and fBm with H>1/2 is too smooth.A model driven by both processes is free of such drawbacks.
Recently,there are a lot of works devoted to Euler approximation of mixed SDEs driven by standard Brownian motions and fBms,e.g.[3,6,8,9].Guerra and Nualart[3]proved an existence and uniqueness theorem for weak solution of SDE(1)on Rd.The proof relies on an estimate of Euler approximation for SDE(1)which was obtained using the methods of fractional integration and the classical It?o stochastic calculus.Mishura and Shevchenko[8]obtained that SDE(1)has a uniqueness strong solution by Euler approximation under some mild regularity assumptions and the space with the norm
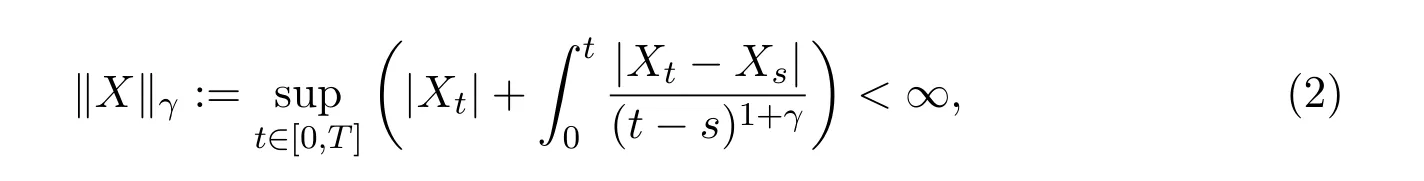
for some γ ∈ (1?H,1/2).In the same year they[9]also considered the following mixed SDE involving both standard Brownian motion and fractional Brownian motion with Hurst index H>1/2,for t∈[0,T],
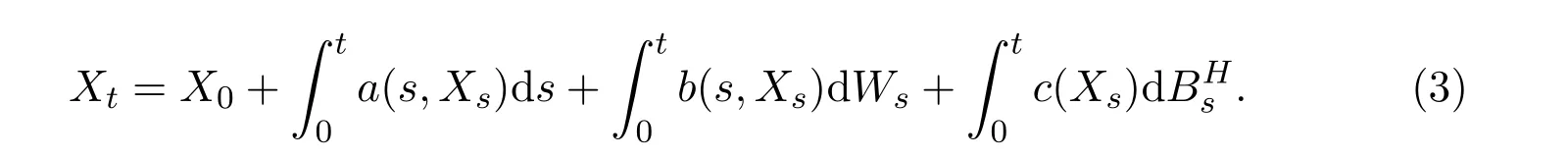
Under the bound of a(t,x),b(t,x),c(x)(c(x)>0)together with their derivatives,and(2H ? 1)-H¨older continuous in time t,they showed that the mean-square rate of convergence of Euler approximation of solution to SDE(3)is.Very recently under the same conditions Liu and Luo[6]got the better mean-square rate of convergence O()by a modified Euler method for SDE(3).
The aim of this paper is to prove that the rate of convergence for Euler approximation of SDE(1)is O(δ2H?2γ)in Besov norm(see Definition 3.1.To the best of our knowledge,up to now,there is no paper investigating the convergent rate for Euler approximation of SDE(1)in Besov norm.Thus,we will make a first attempt to research such problem in the present paper.
The rest of this paper is organized as follows.Some elements of fractional calculus on an interval are give in Section 2.The assumptions are presented and the existence and uniqueness result is shown in Section 3.Then,we devote to Euler approximation for SDE(1)and give the rate of convergence in Section 4.Finally,in Section 6,we make a conclusion of our work.
2 Elements of Fractional Calculus


where Cα,H,εis a constant depending on the underlying arguments with ε< α+H?1.Without loss of generality we can assume that ε=(α+H ?1)/2(see,for example,[13]).Also it is easily obtained from(9)that ψ(ω,α,t) ≤ ψ(ω,α,T)for all ω,α and t ∈ [0,T].Furthermore,for any t ∈ [0,T],the random variables ψ(ω,α,t)are continuous in t and have moments of any order.
Also we need the following corollary from Proposition 4.1 in[13]:For any α∈(1?H,1/2),for all 0≤s≤t≤T and for any function f∈Wα,1(0,T),we have
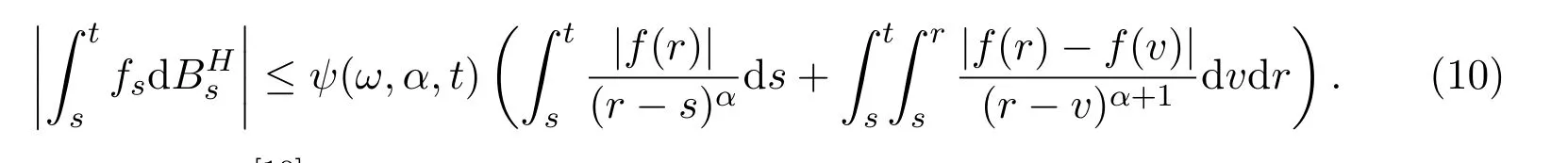
Lemma 2.1[10]For each R > 1 we define the following stopping time τR

Assume that conditions(H1)-(H4)hold.Then P(τR< T)admits the bound μ(R)and tends to 0 when R→∞.
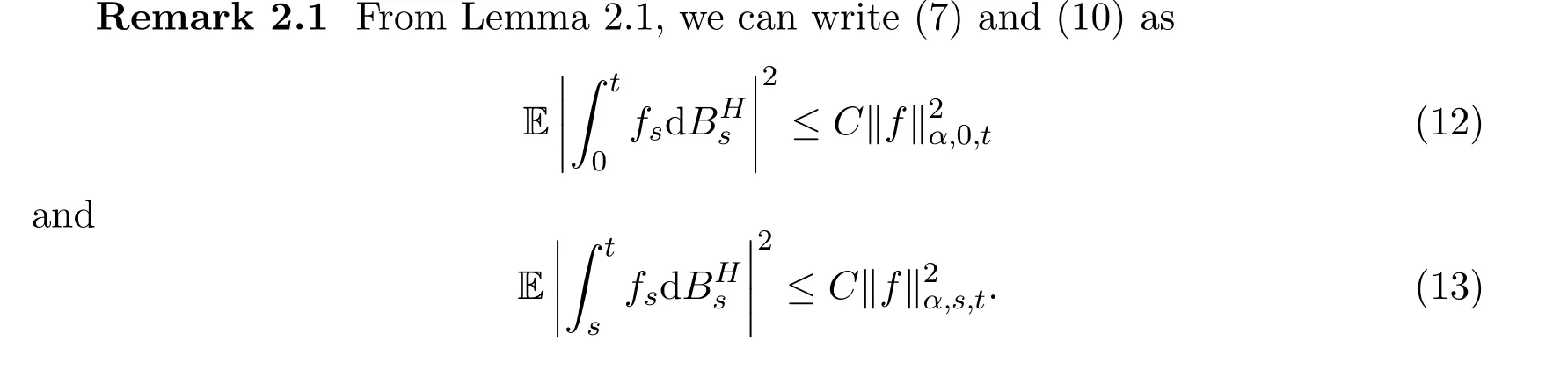
3 Existence and Uniqueness Result in Besov Norm
In this paper,we suppose that the coefficients in SDE(1)satisfy the following hypotheses,which were also used in[10].For simplicity,we denote by C the generic constants whose values are not important and maybe different from line to line.
(H1)The drift coefficient a(t,x)and the diffusion coefficients b(t,x),c(t,x)are bounded,that is,there exists a constant C>0 such that for any t∈[0,T]and any x∈R,
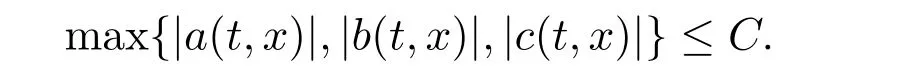
(H2)The functions a(t,x),b(t,x)and c(t,x)are Lipschitz continuous in x,that is,there exists a constant C>0 such that for any t∈[0,T]and any x,y∈R,
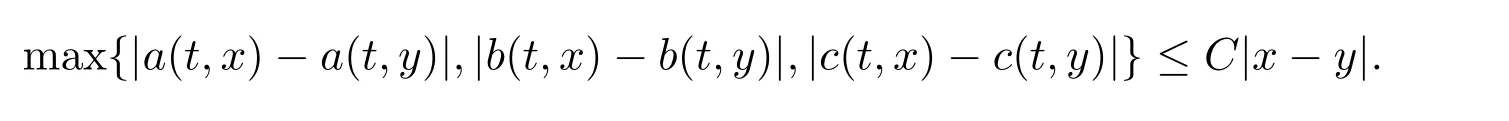
(H3)The diffusion function c(t,x)is differentiable in x and the functions a(t,x),b(t,x),c(t,x)and the partial derivative ?xc(t,x)are β-H¨older continuous in time t,that is,there exist a constant C>0 and a parameter β∈(H,1)such that for any s,t∈[0,T]and any x∈R,

In particular,both the fractional Brownian motion BHwith H>1/2,and the standard Brownian motion W,have their trajectories in Wγ([0,T]).
As was stated in Theorem 2.1 of[8]or Theorem 3.1 of[11],under assumptions(H1)-(H4)with 1?H<β<1,3/2?H<ρ<1,SDE(1)has the unique solution{Xt,t∈[0,T]}and this solution belongs to the stochastic Besov space Wγ([0,T]),1?H <γ< min{β,ρ?1/2}.
4 Euler Approximation in Besov Norm








5 A Numerical Example
Consider the following mixed SDE driven by both Brownian motion and fractional Brownian motion,or,in the integral form,

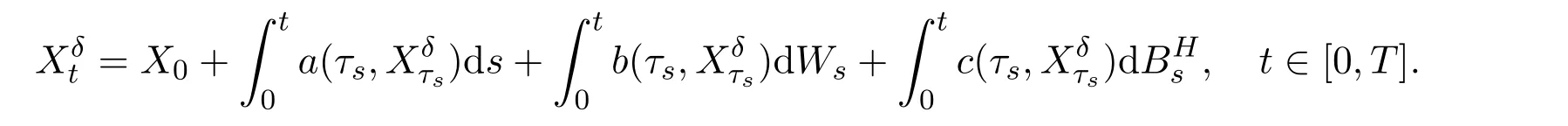
In the M-file EulerMSDE.m we set the initial state of the random number generator to be 100 with the command randn(‘state’,100)and consider(25)with μ =2,σ=1,T=1 and X0=1.We compute a discretized Brownian motion and fBm path over[0,T]with N=28and evaluate the solutions in(26)as Xtrue0T,and then apply Euler approximation using a stepsize δ.The Euler solution is stored in the 1-by-(N+1)array XE0T.The ‖ ·‖-error and the constant C in Theorem 4.1 are computed as XEerrsup and Comega respectively in the M-file EulerMSDE.m.In order to compare different convergent cases,we set H=0.6,0.7,0.75,0.85,α=0.75?0.5H and ρ=γ=min{0.5,2H?1}/2.We get the following numerical results:
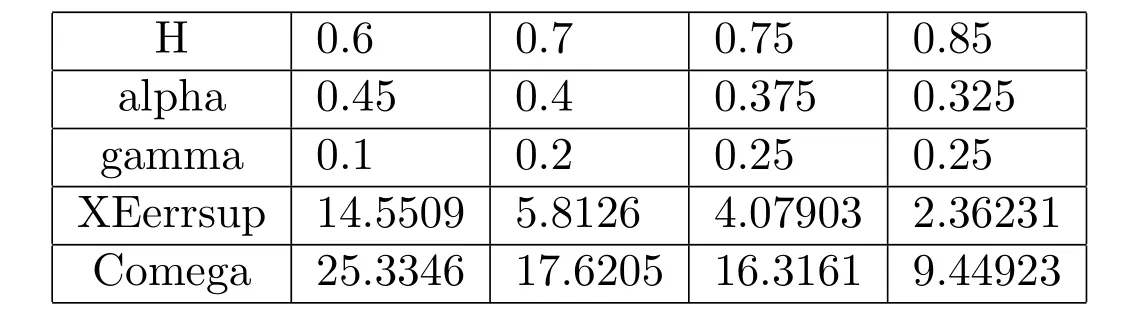
H 0.6 0.7 0.7 5 0.8 5 a l p h a 0.4 5 0.4 0.3 7 5 0.3 2 5 g a m m a 0.1 0.2 0.2 5 0.2 5 X E e r r s u p 1 4.5 5 0 9 5.8 1 2 6 4.0 7 9 0 3 2.3 6 2 3 1 C o m e g a 2 5.3 3 4 6 1 7.6 2 0 5 1 6.3 1 6 1 9.4 4 9 2 3
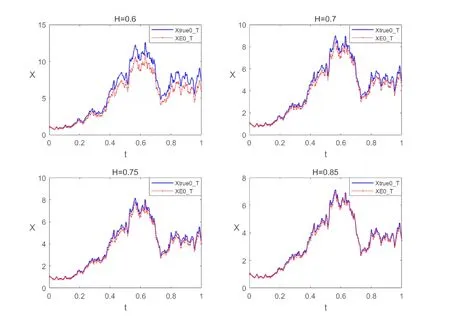
From the table,we can see the larger H,the smaller XEerrsup and Comega,that is the larger H,the smaller error and dominated constant C.From the figure,we can see the larger H,the better the convergence,moreover,the two graphs of H=0.75 and H=0.85 are very similar.These are consistent with our conclusion because the rate of convergence is less than min{0.5,2H?1}(see Theorem 4.1).
6 Conclusions
The following non-autonomous mixed SDEs driven by both Brownian motions and fBms are considered in this paper,for t∈[0,T],
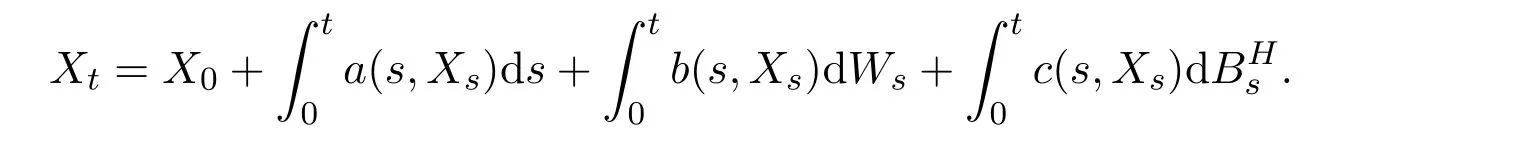
Under assumptions(H1)-(H4),we make a first attempt to obtain that the Euler approximation has the convergent rate O(δ2H?2γ)for γ ∈ (1 ? H,min{β,ρ ? 1/2})in Besov norm ‖·‖γ(see Definition 3.1).
On one hand,as we know,the mean-square rate of convergence for ‘pure’SDE driven by single Brownian motion is O()(see[5])and by single fBm is O(δ2H?1)(see[7]).Comparing mean-square norm with Besov norm,and noting that 2H?2γ<2(2H?1),for mixed SDEs we can only obtain the mean-square rate of less than 2H?1,that is for the mixed SDEs,we can only obtain the worst convergent rate of those of‘pure’SDEs.That is because,for Euler approximation,the estimates for‘pure’SDEs driven by single Brownian or by single fBm are sharp(see[5,12]).
On the other hand,Mishura and Shevchenko[9]researched the Euler approximation of the following one-dimensional mixed SDEs,for t∈[0,T]

They derived the mean-square rate of convergence O(∧(2H?1)).In[6]Liu and Luo obtained a faster rate of convergence O()to(28)by using the modified Euler method.In a forthcoming paper we will study the rate of convergence of modified Euler approximation to SDE(1).
AcknowledgmentThe authors are very grateful to Professor Xuelai Li for his supports and encouragement in making this work possible.We also would like to thank the referees for their valuable remarks and suggestions which led to the improvement of the paper.
 Annals of Applied Mathematics2020年4期
Annals of Applied Mathematics2020年4期
- Annals of Applied Mathematics的其它文章
- INVERSE SCATTERING METHOD AND APPLICATIONS?
- EXTINCTION OF A DISCRETE COMPETITIVE SYSTEM WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE AND THE EFFECT OF TOXIC SUBSTANCES??
- THE GENERALIZED JACOBIAN OF THE PROJECTION ONTO THE INTERSECTION OF A HALF-SPACE AND A VARIABLE BOX?
- EXISTENCE OF UNBOUNDED SOLUTIONS FOR A n-TH ORDER BVPS WITH A p-LAPLACIAN??
- BASIC THEORY OF GENERALIZED p-TYPE RETARDED FUNCTIONAL DIFFERENTIAL EQUATIONS?
- OSCILLATION OF THIRD-ORDER NONLINEAR DELAY DIFFERENTIAL EQUATIONS??
