任興蓉, 趙晶晶

(蘭州交通大學(xué)數(shù)理學(xué)院, 蘭州 730070)

隨著金融業(yè)在國(guó)際市場(chǎng)的影響日益變化, 期權(quán)定價(jià)理論的研究備受關(guān)注,且應(yīng)用也更為廣泛．金融衍生產(chǎn)品的定價(jià)始于對(duì)其基礎(chǔ)資產(chǎn)價(jià)格過程的合理建模, 在著名的Black-Scholes模型中, 股票的價(jià)格被假定為遵循幾何布朗運(yùn)動(dòng)dSt=μStdt+σStdWt, 其中μ為漂移率,St為t時(shí)刻的股票價(jià)格, dt為時(shí)間的微分,σ為波動(dòng)率,Wt為標(biāo)準(zhǔn)布朗運(yùn)動(dòng)．基于市場(chǎng)數(shù)據(jù)的模型校準(zhǔn)是金融研究中的一個(gè)重要問題, 波動(dòng)率是決定金融衍生品的重要參數(shù), 然而波動(dòng)率在市場(chǎng)數(shù)據(jù)中是不可直接觀察的,在這種情況下,對(duì)模型參數(shù)進(jìn)行重構(gòu)通常是一個(gè)反問題．與正問題相比, 在一般情況下, 反問題在Hadamard意義下是不適定的, 即存在性、唯一性和穩(wěn)定性這三者之一不滿足時(shí), 就稱為不適定性問題．因此反問題有著重要的研究和應(yīng)用價(jià)值．

近年來, 隨著金融數(shù)學(xué)的發(fā)展,對(duì)局部波動(dòng)模型的研究引起了學(xué)術(shù)界的廣泛關(guān)注．Ma等[1]針對(duì)期權(quán)定價(jià)反演問題, 提出了求解波動(dòng)率參數(shù)反演的非單調(diào)梯度算法; Zhang[2]研究了美式期權(quán)重構(gòu)光滑局部波動(dòng)率的罰方法; Xu等[3]利用全局收斂的信賴域方法求解Black-Scholes模型參數(shù)反問題; Deng等[4]基于最優(yōu)控制理論,研究了與黃金價(jià)格掛鉤的理財(cái)產(chǎn)品波動(dòng)率的反問題, 并給出了相應(yīng)的數(shù)值實(shí)驗(yàn), 結(jié)果表明該方法能很好地恢復(fù)波動(dòng)率函數(shù); Xu等[5]研究了跳擴(kuò)散過程下期權(quán)定價(jià)模型波動(dòng)率的反問題; 王守磊[6]運(yùn)用二元總變分正則化方法來估計(jì)隱含波動(dòng)率; Doi等[7]基于Black-Scholes模型推導(dǎo)出了一種新型套利模型, 并應(yīng)用微局部分析法,證明了在金融市場(chǎng)上其解的唯一性, 得到一個(gè)相對(duì)穩(wěn)定的算法; Chen等[8]基于最優(yōu)控制理論提出一種重構(gòu)局部波動(dòng)率的方法,證明了極小元滿足的必要條件,并給出了相應(yīng)的數(shù)值算法．還有許多學(xué)者對(duì)重構(gòu)波動(dòng)率的反問題進(jìn)行了研究[9-12],但針對(duì)如何恢復(fù)局部波動(dòng)率的研究并不多,而其理論研究和方法應(yīng)用都具有重要的科學(xué)意義和應(yīng)用價(jià)值．本文擬沿著文獻(xiàn)[8]中的思路,研究從模型市場(chǎng)數(shù)據(jù)中如何恢復(fù)局部波動(dòng)率的反問題,運(yùn)用線性化的方法將原問題轉(zhuǎn)化為重構(gòu)源項(xiàng)的反問題,同時(shí)基于最優(yōu)控制理論討論控制泛函極小元的存在性及滿足的必要條件．

1 問題的簡(jiǎn)述

假設(shè)在風(fēng)險(xiǎn)中性度量下, 基礎(chǔ)資產(chǎn)遵循均值回歸過程dS=α(κ-lnS)Sdt+σSdW, 其中α是均值回歸率,κ表示均值回歸系數(shù), 用C(S,t;K,T)表示基礎(chǔ)資產(chǎn)在t時(shí)刻的歐式看漲期權(quán)價(jià)格,執(zhí)行價(jià)格為K,到期日為T,則歐式看漲期權(quán)價(jià)格C(S,t;K,T)滿足Black-Scholes方程

(1)

利用基本解的性質(zhì),可將此問題轉(zhuǎn)化為一個(gè)具有終端觀測(cè)值的反問題．當(dāng)局部波動(dòng)率σ僅為S的函數(shù)時(shí), 令G(S,t;K,T)=CKK(S,t;K,T), 則式(1)轉(zhuǎn)化為

其中δ(S-K)是在K點(diǎn)的Dirac函數(shù)．可以證明G(S,t;K,T)是(K,T)對(duì)偶算子的基本解,則G滿足

(2)

令U(S,t;K,τ)=CK, 其中τ=T-t, 結(jié)合式(1)和(2)得

(3)

其中H是Heviside函數(shù)．通過變量替換:y=ln(K/S*),a(y)=σ2(K)/2,b(y)=α(y+lnS*-κ),V(y,τ)=erτU(S*,t*;K,τ), 方程(3)可轉(zhuǎn)化為

(4)

本文的問題是求得一個(gè)a(y)使其成為方程(4)相應(yīng)的解, 附加條件為V(y,τ*)=V*(y),y∈R．然而該反問題是非線性的, 求解的過程比較困難, 而線性化法是一種比較容易的方法．

將問題(4)線性化[13]．假設(shè)a(y)=a0+f(y), 其中f(y)是a0的小擾動(dòng), 且f≠0．令V=V0+U+v, 其中V是帶擾動(dòng)解U的主要部分,v是關(guān)于f的高階小量(可忽略不計(jì)),V0是q(y)=q0時(shí)方程(4)的解, 易驗(yàn)證U滿足方程

(5)

其中V0y是一個(gè)已知且確定的函數(shù)．令R1(y,τ)fy+R2(y,τ)f=(fV0y)y+fV0y, 則原問題可以表示為

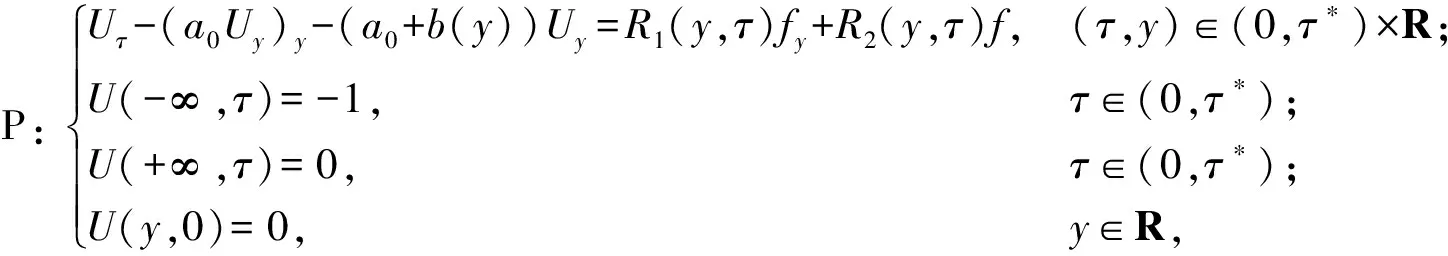
(6)

其中a0是已知的參數(shù);b(y)是已知的函數(shù);f是方程(6)未知的右端項(xiàng),稱為方程的源項(xiàng); 附加條件為

U(y,τ*)=U*(y),y∈R,

(7)

則該如何確定滿足方程(6)和(7)的函數(shù)組(U,f)?

2 最優(yōu)控制問題

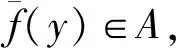
(8)

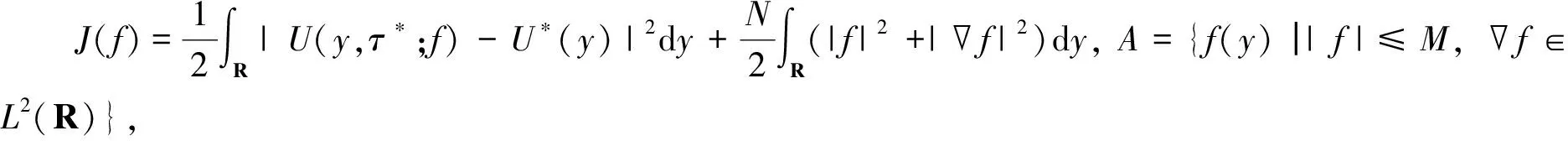
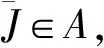
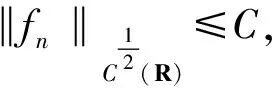
3 必要條件

定理2若f是最優(yōu)控制問題(8)的解, 則存在一個(gè)三元函數(shù)組(U,φ,f)滿足方程組

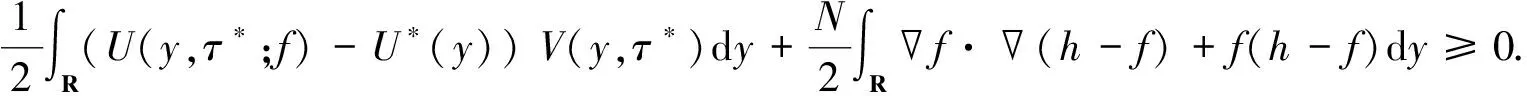
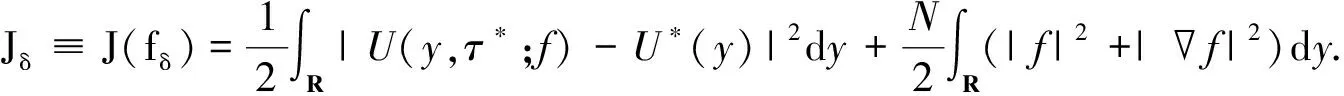
(9)

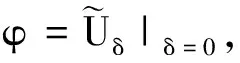
(10)

4 結(jié)論

本文運(yùn)用偏微分方程的最優(yōu)控制理論,探討了局部波動(dòng)率系數(shù)的存在性,并且證明了最優(yōu)解所滿足的必要條件．這些結(jié)果為數(shù)值模擬奠定了基礎(chǔ),并且可以為一些金融行業(yè)工作者提供恰當(dāng)?shù)膮⒖迹?/p>