蔣新雅, 周正新

(揚(yáng)州大學(xué)數(shù)學(xué)科學(xué)學(xué)院, 江蘇 揚(yáng)州 225002)

對(duì)于平面微分系統(tǒng)

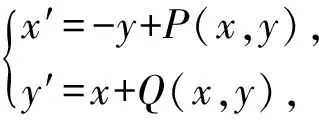
(1)

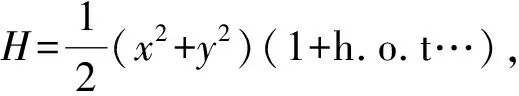
(2)

以(0,0)為中心的充要條件, 其中Φ2,Φ6分別為關(guān)于x,y的二次和六次齊次多項(xiàng)式,μi,ai∈R(i=1,2)．

1 主要結(jié)果

在極坐標(biāo)系下微分系統(tǒng)(1)可化為:

(3)

由文獻(xiàn)[3,18]知, 若存在連續(xù)可微的2π周期函數(shù)u(θ)和連續(xù)可微函數(shù)fk(u),gk(u)使得Ak(θ)=u′(θ)fk(u(θ)),Bk(θ)=gk(u(θ)), 則稱2π-周期方程(3)滿足復(fù)合條件．

引理1[3]若微分方程(3)滿足復(fù)合條件, 則微分系統(tǒng)(1)以原點(diǎn)為中心,且這個(gè)中心稱為復(fù)合中心．

(4)

情形1若μ2≠0, 作變換X=x/μ2,Y=y/μ2,上式化為

(5)

其中μ=μ1/μ2,P2=∑i+j=2pijxiyj,P6=∑i+j=6pijxiyj,pij∈R．

定理1若μ=1,且

(6)

則微分系統(tǒng)(5)以(0,0)為中心的充要條件為

(7)

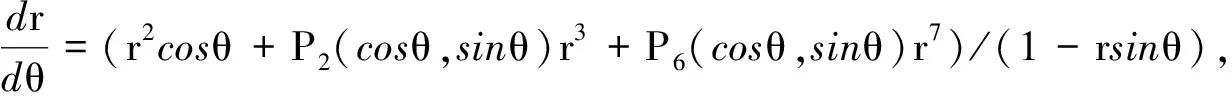
(8)

(9)

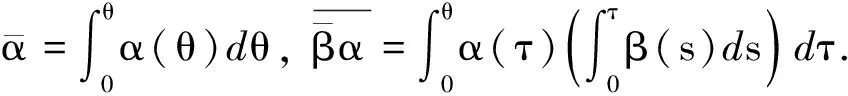
(10)

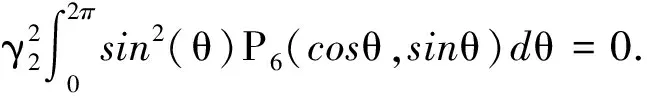
(11)

(12)

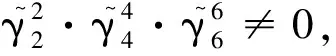
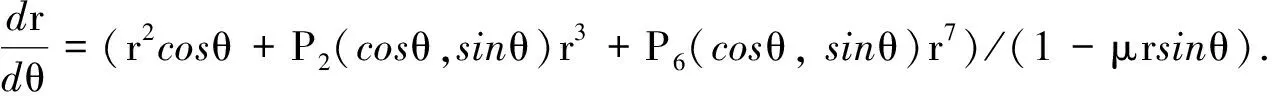
情形2若μ2=0,μ1≠0, 微分系統(tǒng)(4)化為

(13)

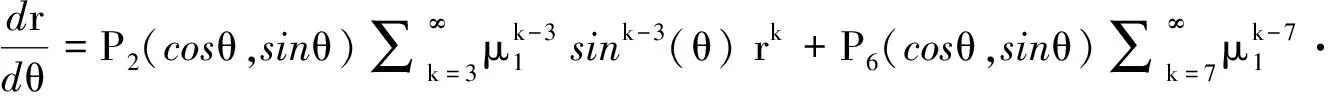
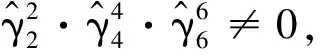
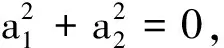
(14)

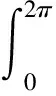
綜上微分系統(tǒng)(4)的Poincaré-中心焦點(diǎn)問題已全部解決．