A New Non-Parameter Filled Function for Global Optimization Problems
(1.School of Science,Hebei University of Technology,Tianjin 300401,China;2.School of Mathematics and Statistics,Henan University of Science and Technology,Luoyang 471000,China)
Abstract:In the paper,to solve the global optimization problems,we propose a novel parameter-free filled function.Based on the non-parameter filled function,a new filled function algorithm is designed.In the algorithm,the selection and adjustment of parameters can be ignored by the characteristic that the filled function is parameter-free.In addition,in the region lower than the current local minimizer of the objective function,the filled function is continuously differentiable which enables any gradient descent method to be used as a local search method in the algorithm.Through numerical experiments by solving two test problems,the effectiveness of the algorithm is verified.
Keywords:Global optimization;Non-parameter filled function;Box constraint
§1.Introduction
Many problems in finance,engineering,management and social sciences can be solved via the global optimization methods.It is usually difficult to find the global minimizer for such problems.Because of the existence of multiple local minimizers for general multimodal functions,traditional optimization methods[9]often confined to a local minimizer lead to the best local minimizer cannot be found.
There are many ways to solve global optimization problems,including stochastic methods and deterministic methods.The filled function method is a deterministic method that can effectively solve general global optimization problems without specific structures.The main idea of filled function method is that modifies the objective function as a filled function and then obtains a best local minimizer frequently by optimizing the filled function formed on the minimizer found previously.The current local minimizer can be jumped out by minimizing the filled function.The filled function method consists of two parts:one is local minimization and the other is to fill.In the minimization phase,a local minimization algorithm is used to obtain a local minimizer of the original problem.In the filling phase,the original problem is minimized by means of the filled function,the two phases are alternated until a global minimizer is found.
The concept of filled function and the filled function method were firstly introduced by Ge[3–5].Subsequently,the form of filled function has been continuously improved and the filled function method is becoming more perfect and mature[6,8,11–14].Theoretical and numerical calculations show that the filled function method is a very effective global optimization method.However,because many of existing filled functions rely heavily on the selection of parameters.How to select the appropriate parameters in the actual calculation process directly affects and determines the operation speed and efficiency.In addition,most filled functions are non-differentiable or even discontinuous,which makes the local search is difficult.
The main purpose of the paper is to introduce and formalize a new non-parameter filled function which is continuously differentiable in the region lower than the current local minimizer of the objective function.Firstly,we provide formal definitions and assumptions.Next,we offer and investigate the theoretical prosperities of the filled function and propose the solution algorithm.Finally,we report experimental results by applying the algorithm on several test problems to confirm the effectiveness of the new method.
§2.A new filled function and its properties
The following global optimization problem will be discussed:

wheref:Rn→R.
Throughout this paper,we assume that the following conditions are satisfied.
Assumption 2.1.f(x)is a coercive function,i.e.,when‖x‖→+∞,then f(x)→+∞.
Lemma 2.1.(Theorem 2.14 in[2]).Let f:Rn→(-∞,∞]be a proper closed and coercive function and let C?Rn be closed set.If C∩dom(f)/=?.Then f can attain its minimal value over C.
By Assumption 2.1 and Lemma 2.1,the original problem is equivalent to the following problem:
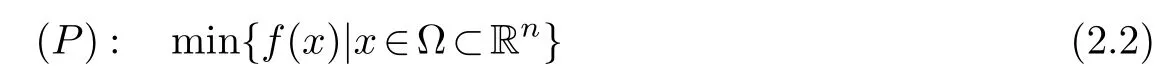
where setΩ?Rnis a closed.
Assumption 2.2.The set F={f(x*)|x*∈L(P)}is finite,where L(P)is the set of all minimizers of problem(2.2).
Note that Assumption 2.2 only requires that the number of local minimal values of problem(2.2)is finite.The number of local minimizers can be infinite.
Assumption 2.3.f(x)is continuously differentiable onΩ∈Rn.
Definition 2.1.(see[12])A function P(x,,f(x))is called a filled function of f(x)atwhich is the current local minimizer of f(x),just if
(x,,f(x)).
2.For all x∈Ω1,there is no stationary of function P(x,,f(x))that is0/∈?P(x,,f(x)),whereΩ1={x∈Ω|f(x)≥f(),x/=}.
3.IfΩ2={x∈Ω|f(x)<f()}is not empty,then?x′k∈Ω2and x′k is a local minimizer offunction P(x,,f(x)).
In the following,we propose a new non-parameter filled function,
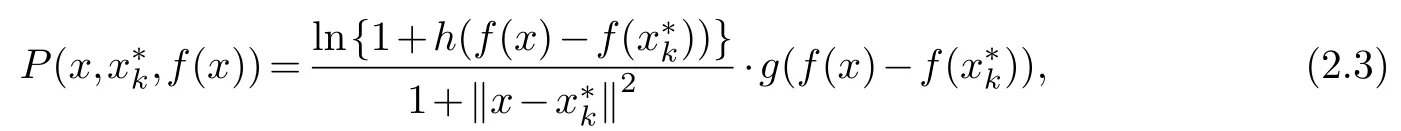
whereis a local minimizer off(x),.
It is obvious thath(t)andg(t)are continuously differentiable functions int≥0 andt<0 respectively.It implies the filled function is continuously differentiable inΩ1andΩ2respectively.
The new filled function keeps basic characteristics and overcomes the shortcomings of the conventional filled functions.Firstly,it is continuously differentiable in the region lower than the current local minimizer of the objective function,which makes it easier for the filled function to obtain its local minimizers by an existing local optimization method.Secondly,it does not contain any parameters that need to be adjusted compared with other filled functions.The following theorems(Theorems 2.1-2.3)show thatP(x,,f(x))is a filled function which satisfies the conditions of Definition 2.1.
Theorem 2.1.is a strict local maximizer of P(x,,f(x))whenis a local minimizer of f(x).
Proof.Sinceis a local minimizer off(x)and existsδ=U(,ε),whereδis a neighborhood of,ε>0 is a sufficient small positive number.When?x∈δandx/=,we havef(x)≥f().Then we obtain
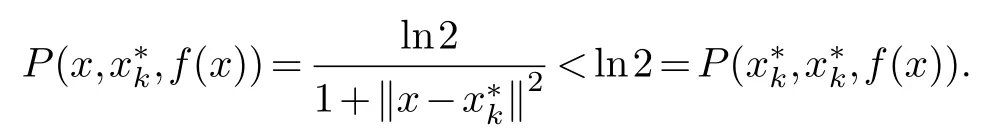
Theorem 2.2.The subgradient of P(x,,f(x))is non-zero onΩ1,that is0/∈?P(x,,f(x))whenis a local minimizer of f(x).
Proof.?x∈Ω1,f(x)≥f(),we obtain
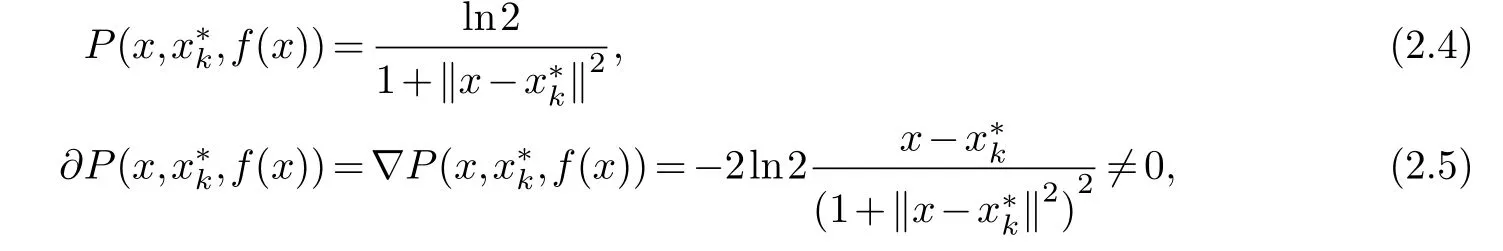
which completes the proof.
Theorem 2.3.Assume thatis not a global minimizer of f(x),then there is a point x′k∈Ω2which is a local minimizer of P(x,,f(x))such that f(x′k)<f().
Proof.is not a global minimizer off(x),it means?x*∈Ω2such thatf(x*)<f().

By Assumption 2.1,?y∈?Ω,f(y)>f()theny∈Ω1such that
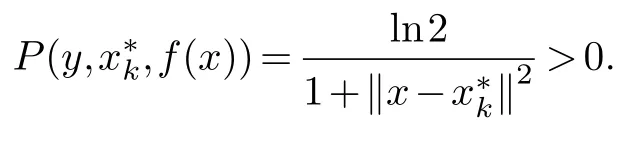
By the intermediate value theorem of continuous function,there isz′∈{z∈[x*,y]|P(z,,f(x))=0},that is a point on the segment betweenx*andy,the function value ofPat this point is 0.Assume thatzis the closest point tox*on the segment[x*,y]withP(z,,f(x))=0.LetS(x*)as the set of all the above line segments[x*,z]wheny∈?Ωsuch thatS(x*)is a closed region.By continuity ofP(z,,f(x)),there isx′k∈S(x*)which is the local minimizer ofP(x,,f(x))such thatP(x′k,,f(x))<0.SinceP(x,,f(x))is continuously differentiable onΩ2,then?P(x′k,,f(x))=0.Hence,there is a pointx′k∈Ω2which is a local minimizer ofP(x,,f(x)),it holds thatf(x′k)<f(),which completes the proof.
Theorems 2.1-2.3 guarantee that the filled function(2.3)is proposed in this section is a continuous differentiable function in the region lower than the current local minimizer of the objective function.In order to further explain the effectiveness of the filled function in theory,the following analysis is made on the change of the function value of the filled function when leaving the local minimizer.
Theorem 2.4.If x1,x2∈Ω1and‖x2-‖>‖x1-‖,then P(x2,,f(x))<P(x1,,f(x)).
Proof.x1,x2∈Ω1and‖x2-‖>‖x1-‖,we obtain
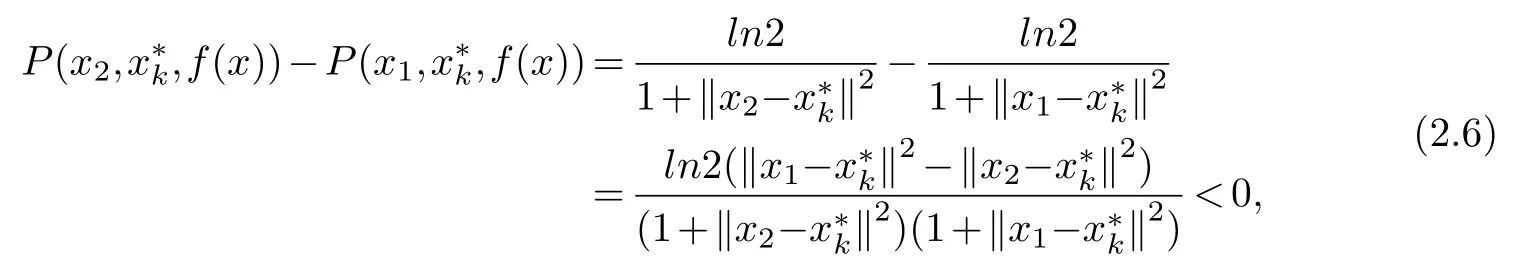
which completes the proof.
Theorem 2.5.If x1∈Ω1,x2∈Ω2,then P(x2,,f(x))<P(x1,,f(x)).
Proof.x1∈Ω1,x2∈Ω2,By the definition ofΩ1andΩ2,we deduce that
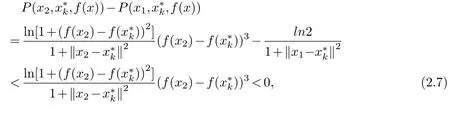
which completes the proof.
Theorem 2.6.If x1,x2∈Ω2,f(x1)≥f(x2)and‖x2-‖>‖x1-‖,then P(x2,,f(x))<P(x1,,f(x)).
Proof.Sincex1,x2∈Ω2,‖x2-‖>‖x1-‖.f(x2)≤f(x1)andf(x2)-f()≤f(x1)-f()<0,then(f(x2)-f())2≥(f(x1)-f())2.We have
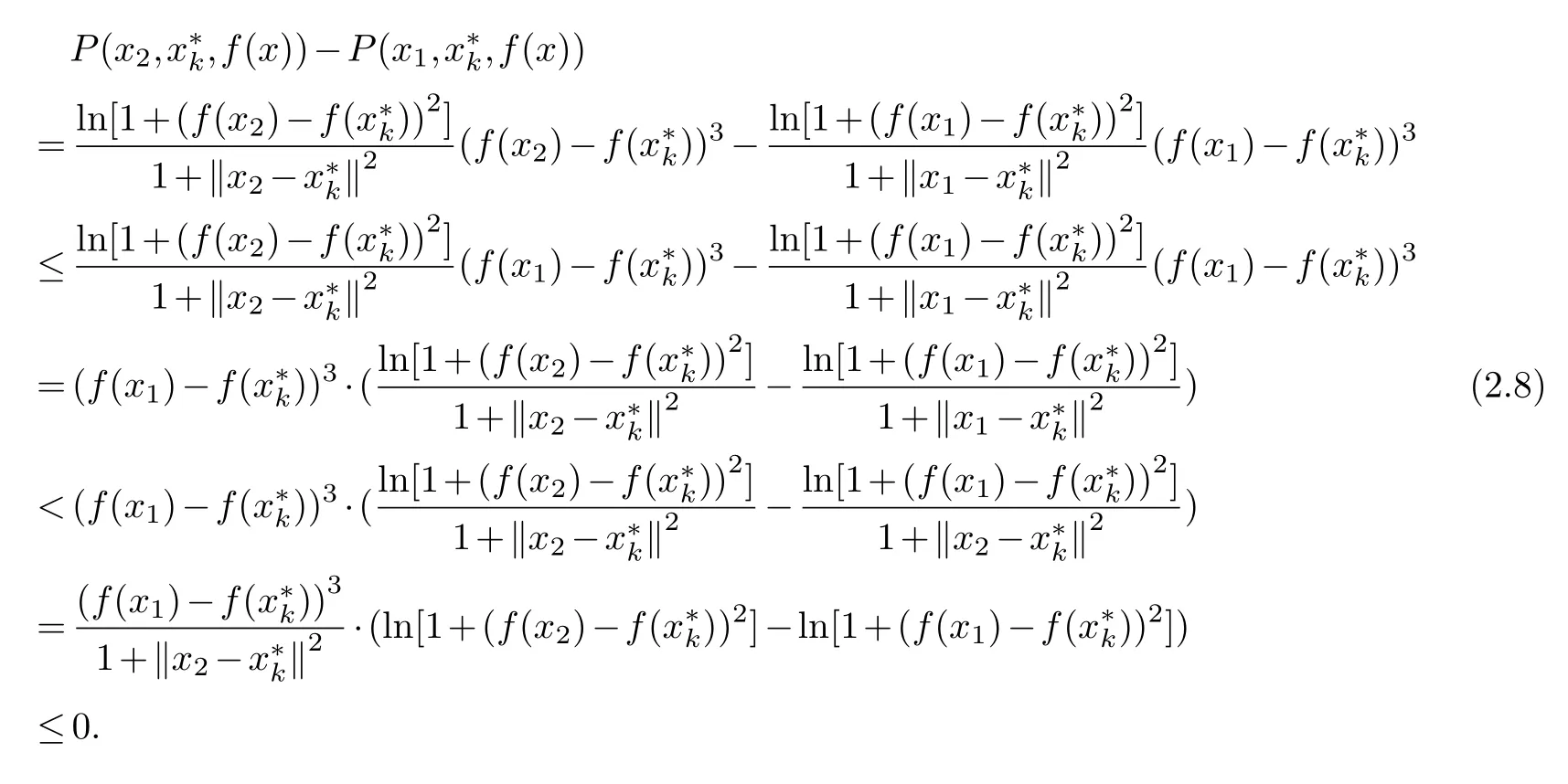
Therefore,P(x2,,f(x))<P(x1,,f(x)),which completes the proof.
Theorems 2.4-2.6 show that when leaving,the value of the filled function decreases,that is,x∈Ω2,f(x)<f()can be obtained.Theorems 2.4-2.6 can ensure that the sequence obtained by minimizing the filled function converges to a better minimizer than the current minimizer off(x).
§3.Filled function algorithm
From the construction ofP(x,,f(x)),ifis not the global minimizer of(P),i.e.,Ω2/=?.By minimizing the filled functionP(x,,f(x)),we can obtain a better pointxof problem(P)withf(x)<f().Thus a better local minimizerof problem(P)is obtained by minimizing thef(x).Repeating this process,we can finally obtain a solution or an approximate solution of problem(P).
Based on the theorems and discussions in the above,a novel filled function algorithm for solving problem(P)is described as follows.
Step 0,Select initial pointxk∈Ω,setk=1.
Step 1,Fromxkof local search,the local minimizeris obtained by minimizingf(x).
Step 2,Select sequence set{xik|i=1,2,···m}at the neighborhood of,wherem≥2n.
Step 3,Seti=1.
Step 4,Ifi≤m,go to Step 5;otherwise,it means that a smaller point cannot be found by starting from any point in{xik},takeas the global minimizer,terminate the algorithm.
Step 5,Ifxik∈Ω,go to Step 6;otherwise,i=i+1,go to Step 4.
Step 6,Setx:=xik,iff(x)<f(),setxk:=x,k:=k+1,go to Step 1,otherwise,go to Step 7.
Step 7,(1)Constructing a filled function:
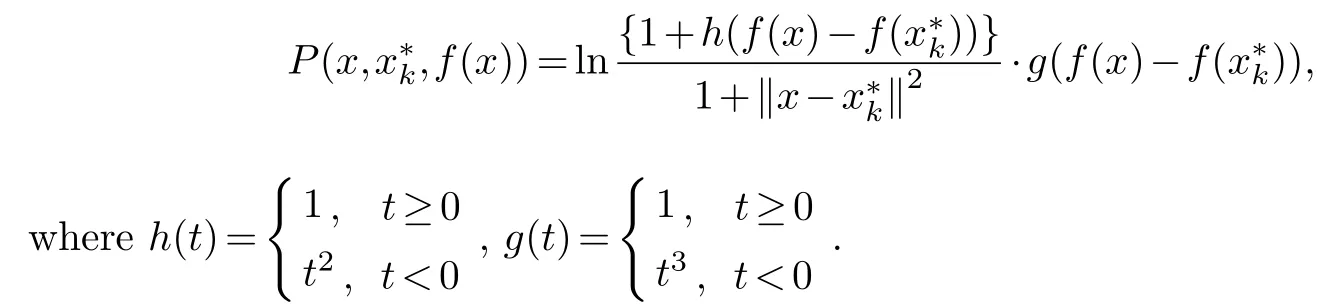
(2)Usexas an initial point to minimizeP(x,,f(x)),get its local minimizerx*.
Step 8,Iff(x*)<f(),setk=k+1,xk=x*,go to Step 1,otherwise,seti=i+1,go to Step 4.
Remark 3.1.N(,δk)is a neighborhood of,whereis the k-th local minimizer,x is the starting point in the k-th iteration in finding the k-th local minimizer,we takeδk as.
Remark 3.2.In the algorithm,we can use any local optimization algorithm to realize local optimization,such as Hybrid Hooke-Jeeves direction algorithms[10],Powell’s method[7]and Mesh adaptive direct search algorithms[1].Hybrid Hooke-Jeeves direction algorithms are better than other methods,because these algorithms ensure that local minimizers of box constrained optimization problems can be found.Hooke-Jeeves method is used as local optimization method.
§4.Numerical experiment
In the section,we implement numerical tests for two examples.All these tests are programmed in a computer with an Intel(R)Core(TM)i5-7500CPU@3.40GHz8G in Matlab R2010b.
In the section,Hooke-Jeeves method is used as local optimization method.
The main iterative results are summarized in tables for each function.The symbols used are shown as follows:
k:The iteration number in finding thek-th local minimizer.
xk:The starting point in thek-th iteration in finding thek-th local minimizer.
f():The function value of thek-th local minimizer.
4.1.Pro.1.
minf(x)=-20exp+20
s.t.≤300,
2x1+x2≤4,
|xi|≤30,i=1,2.
Its global minimizer isx*=(0,0)T,f(x*)=-2.7183.The proposed filled function approach succeeds in identifying a global minimum solution(see Table1).

Table 1 The number solution of Problem 1
4.2.Pro.2.
minf(x)=
s.t.|xi|≤3,i=1,2.
Its global minimizer isx*=(-0.0898,-0.7127)orx*=(0.0898,0.7127),f(x*)=-1.0316.The proposed filled function approach succeeds in identifying a global minimum solution(see Table2).
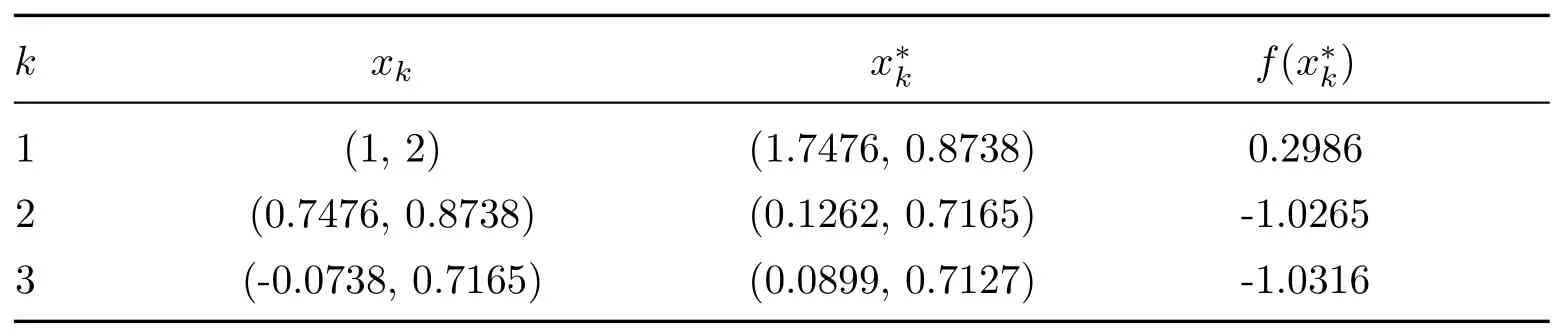
Table 2 The number solution of Problem 2
§5.Conclusion
In the paper,a new filled function without parameters is constructed.Based on the constructed filled function,a new filled function algorithm is designed.In the algorithm,the selection and adjustment of parameters can be ignored by the characteristic that the filled function is parameter-free.In addition,in the region lower than the current local minimizer of the objective function,the filled function is continuously differentiable enables any gradient descent method to be used as a local search method in the algorithm.Through numerical experiments by solving 2 test problems,the effectiveness of the algorithm is verified.
 Chinese Quarterly Journal of Mathematics2021年2期
Chinese Quarterly Journal of Mathematics2021年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- 《數(shù)學季刊》征稿簡則
- Exponential Growth of Solutions for Nonlinear Coupled Viscoelastic Wave Equations with Degenerate Nonlocal Damping and Source Terms
- Auslander Categories and Free Normalizing Extensions
- Painlev′e Analysis of Higher Order Nonlinear Evolution Equations with Variable Coefficients
- A Hovey Triple Arising from a Frobenius Pair
- Entropy and Similarity Measure for T2SVNSs and Its Application
