Auslander Categories and Free Normalizing Extensions
(School of Mathematics and Physics,Anhui University of Technology,Maanshan 243032,China)
Abstract:Let RCS be a semidualizing(R,S)-bimodule.Then RCS induces an equivalent between the Auslander class AC(S)and the Bass class BC(R).Let A and B be free normalizing extensions of R and S respectively.In this paper,we prove that HomS(BBS,RCS)is a semidualizing(A,B)-bimodule under some suitable conditions,and so HomS(BBS,RCS)induces an equivalence between the Auslander class and the Bass class Furthermore,under a suitable condition onRCS,we develop a generalized Morita theory for Auslander categories.
Keywords:Semidualizing module;Auslander class;Excellent extension
§1.Introduction
LetRbe a ring.Mod-Rdenotes the category of all rightR-modules,andR-Moddenotes the category of all leftR-modules.
Over a commutative,noetherian local ring,semidualizing modules provide a common generalization of a dualizing module and a free module of rank one.Foxby[6]first defined them(PG-modules of rank one).In[8],Henric Holm and Diana White extended the definition of semidualizing(S,R)-bimodules,whereRandSare arbitrary associative rings,which are defined as follows:An(R,S)-moduleRCSis semidualizing if
(a1)RCadmits a degreewise finiteR-projective resolution(i.e.,there exists a resolution···→P1→P0→M→0 where eachPiis finitely generatedR-projective).
(a2)CSadmits a degreewise finiteSop-projective resolution.
(b1)The natural homothety mapRRR→HomSop(C,C)is an isomorphism.
(b2)The natural homothety mapSSS→HomR(C,C)is an isomorphism.
A semidualizing module over a commutative noetherian ring gives rise two full subcategories of the category ofR-modules,namely the so-called Auslander classAC(R)and Bass classBC(R)defined by Avramov and Foxby[1,6].Semidualizing modules and their Auslander(resp.,Bass)classes have caught the attention of several authors,see for example[1–7].Henric Holm and Diana White also extended the definitions of Auslander classes and Bass classes to non-commutative non-noetherian rings.The Auslander classAC(S)is defined as follows:theAuslander class with respect to C,denoted byACorAC(S),consists of allS-modulesMsatisfying
(c)The natural mapμCCM:M→HomR(C,C?R M)is an isomorphism.
We will writeμM=μCCMif there is no confusion.Dually,we can defineBC(R).
LetRbe commutative and noetherian.Christensen[2]proved that ifψ:R→Sis local and flat,thenCis semidualizing forRif and only ifC?R Sis semidualizing forS.This result is the motivation for our Theorem 2.1.LetSbe a ring and letRbe a subring ofS(with the same 1).Sis called a finite normalizing extension ofRif there exist elementsa1,a2,...an∈Ssuch thatS=aiRwhereaiR=Raifori=1,2,...n.Finite normalizing extensions have been studied in many papers such as[9–15].Sis called a free normalizing extension ofRifS=aiRis a normalizing extension ofRandSis free with basis{a1=1,a2,...,an}as both a rightR-module and a leftR-module.
LetAandBbe the free normalizing extensions ofRandSrespectively.LetSCRbe a semidualizing(R,S)-bimodule.We get the semidualizing(A,B)-bimodule with respect toRCS.Under a suitable condition onRCS,we develop a generalized Morita theory for Auslander categories.
§2.Auslander categories and free normalizing extensions
In this section,we will give our main results.
Theorem 2.1.Let A=Rai and B=Sbj be left and right free normalizing extensionsof R and S respectively,where each ai centralizes the elements of R and bj centralizes theelements of S.Suppose rijkc=csijk for all c∈C and all i,j,k;where put aiaj=rijhahand bibj=sijhbh.
(1)If RCS is a bimodule,SEndR(RCS)and R~=EndS(RCS),then

as ring isomorphism.
(2)If RCS is a semidualizing(R,S)-bimodule,then Hom(B,RCS)is a semidualizing(A,B)-bimodule,and

defines an equivalent.
Proof.(1)See[16],Theorem 1.1.
(2)First,we shall show thatAHom(BBS,RCS)admits a degreewise finiteA-projective resolution.AsR-modules we haveHom(BBS,RCS).ThenHom(BBS,RCS)has a degreewise finiteR-projective resolution
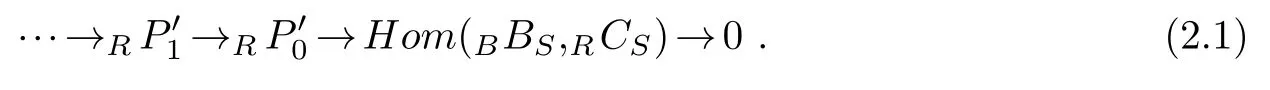
ApplyingAAR?R-to(2.1),we get

where eachAARR P′iis a finitely generated projectiveA-module for alli=0,1,2,···.By(1),Hom(BBS,RCS)is also anA-module.So we define the map
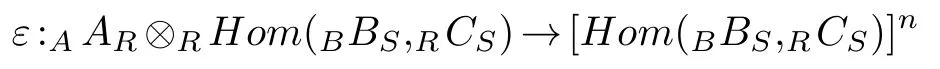
byε(a?f)(b)=Clearlyεis anA-module isomorphism.ThenAHom(BBS,RCS)has a degreewiseA-projective resolution.Similarly,ifRCShas a degreewise finiteS-projective resolution,thenHom(BBS,RCS)has a degreewise finiteB-projective resolution.
Next,we shall show that
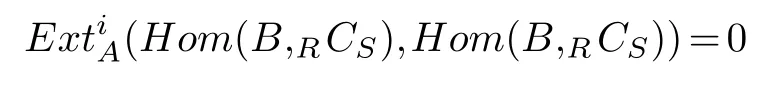
and
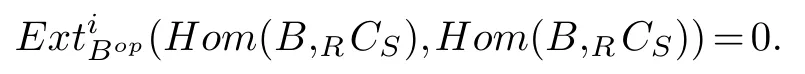
We only show(Hom(B,RCS),Hom(B,RCS))=0.In fact,everyA-module isRmodule,thus(M,N)=0 implies(M,N)=0.We have
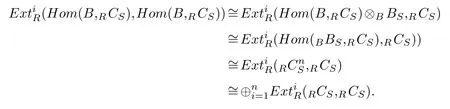
Then(Hom(BBS,RCS),Hom(BBS,RCS))=0.Hom(BBS,RCS)is a semidualizing(A,B)-bimodule and
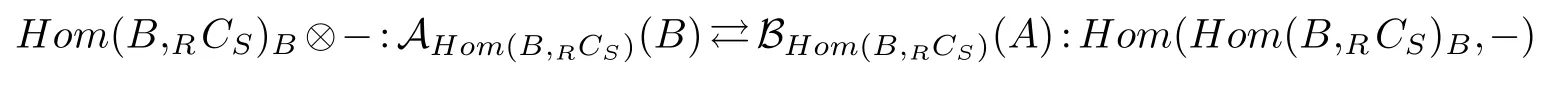
defines an equivalent by[8].
Corollary 2.1.Let A=Rai be a free normalizing extension of R,where each ai centralizesthe elements of R.Suppose rijkc=crijk for all c∈C and all i,j,k;where put aiaj=.
If RCR is a semidualizing(R,R)-bimodule,then Hom(A,C)is a semidualizing(A,A)-bimodule,and the following holds for an A-module F:
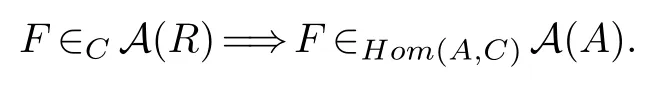
In the rest of this section,we shall discuss generalized Auslander classes and extension rings.
Definition 2.1.Let RCS be an(R,S)(RCS).Define
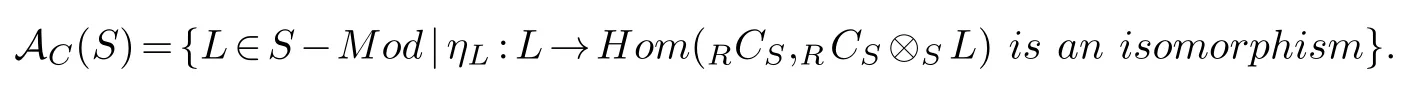
Let RCS be an(R,S)-bimodule,and S~=EndR(RCS).Define
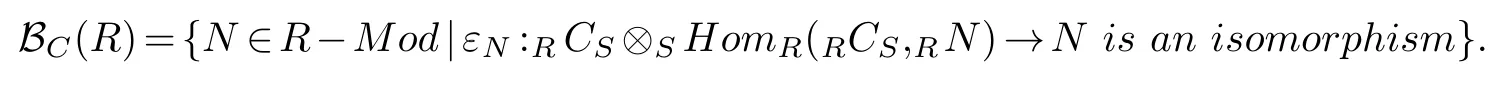
Proposition 2.1.Let RCS be an(R,S)-bimodule with R~=HomS(RCS,RCS)(RCS).
Then RCS?-:AC(S)BC(R):Hom(RCS,-)defines an equivalence.
Theorem 2.2.(1)Let RCS be a finitely generated projective S-module,and REndS(RCS).
Then we have the following adjoint equivalence of categories
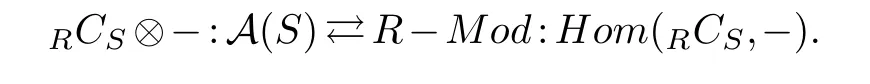
(2)Let RCS be a finitely generated projective S-module,and SEndR(RCS).Then we have the following adjoint equivalence of categories
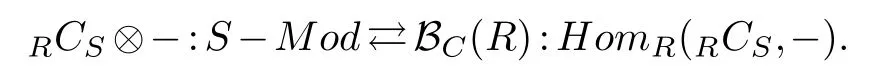
Proof.(1)We begin by observing that for anyR-moduleM,the moduleHom(RCS,RM)in fact is an object ofAC(S).Note that,
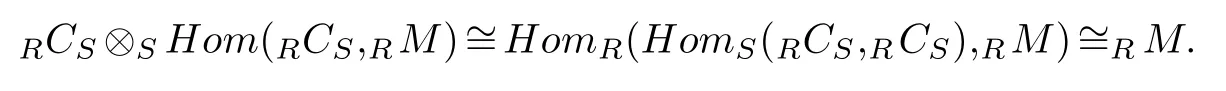
Thus,
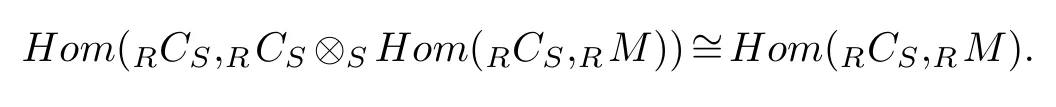
We now need to show that the adjoint pair is an equivalence ifRNR-Mod.SinceRCS?S Hom(RCS,RM),the adjoint pair is an equivalence.
(2)Similar to the proof of(1).
Remark 2.1.Theorem 2.2 is a variant of Morita theory.If CS is a finitely generated projective generator and REndS(CS),we have that the category of R-modules is equivalent to the category of S-modules over S.Theorem 2.2 states that if CS is a finitely generated projective module,then the category of R-modules is equivalent to the subcategory AC(S)of S-modules.
Proposition 2.2.Let A=Rai and B=Sbj be left and right free normalizingextensions of R and S respectively,where each ai centralizes the elements of R and bj centralizesthe elements of S.Suppose rijkc=csijk for all c∈C and all i,j,k;where put aiaj=and bibj=
(1)Let RCS be a finitely generated projective Sop-module,and R~=End(RCS).Then wehave the following adjoint equivalence:
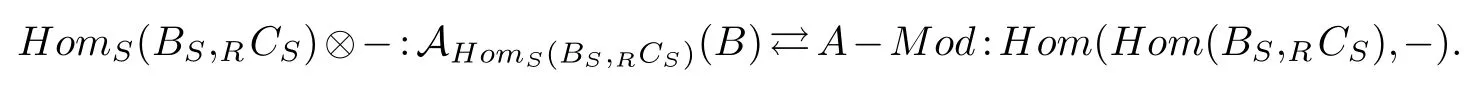
(2)Let RCS be a finitely generated projective Sop-module,and S~=End(RCS).Then we have the following adjoint equivalence:
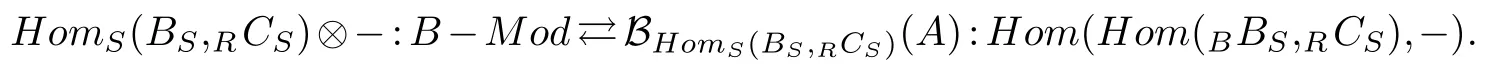
Proof.Note that the proofs of(1)and(2)are similar,so we only show(1).SinceRCSis a finitely generated projectiveS-module,Hom(BBS,RCS)is a finitely generated projectiveB-module.By Theorem 2.1(1),
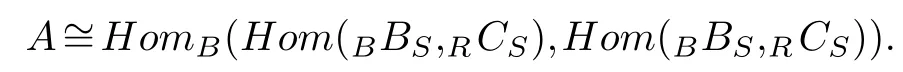
Thus,Hom(BBS,RCS)defines an equivalence by Theorem 2.2.
Acknowledgements
We are greatly indebted to the anonymous referee for helpful comments and stimulating hints.
 Chinese Quarterly Journal of Mathematics2021年2期
Chinese Quarterly Journal of Mathematics2021年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- 《數(shù)學(xué)季刊》征稿簡則
- Exponential Growth of Solutions for Nonlinear Coupled Viscoelastic Wave Equations with Degenerate Nonlocal Damping and Source Terms
- Painlev′e Analysis of Higher Order Nonlinear Evolution Equations with Variable Coefficients
- A New Non-Parameter Filled Function for Global Optimization Problems
- A Hovey Triple Arising from a Frobenius Pair
- Entropy and Similarity Measure for T2SVNSs and Its Application
