(Fundamental Education Department,Shanxi Institute of Energy,Jinzhong 030600,China)

Abstract:There is a close relationship between the Painlev′e integrability and other integrability of nonlinear evolution equation.By using the Weiss-Tabor-Carnevale(WTC)method and the symbolic computation of Maple,the Painlev′e test is used for the higher order generalized non-autonomous equation and the third order Korteweg-de Vries equation with variable coefficients.Finally the Painlev′e integrability condition of this equation is gotten.

Keywords:Higher order generalized non-autonomous equation;Third order Korteweg-de Vries equation with variable coefficients;Painlev′e analysis method

§1.Introduction

The research on integrability of nonlinear systems is one of the topics that many experts and scholars are interested in.However,so far,there has been no uniform definition to judge whether a nonlinear system is integrable,but some integrability concepts in different meanings are given.For example,the nonlinear evolution equation that can be solved by the backscatter method is called IST integrableLax integrableLiouville integrable and Painlev′e integrable[2,8,11].

Painlev′e integrability,which is the focus of this paper,refers to a nonlinear system with Painlev′e properties.The Painlev′e property of a nonlinear evolution equation is closely related to other integrability.The test method of Painlev′e property can not only test whether the equation is Painlev′e integrable,but also obtain some other integrable properties of the equation.For example,when the nonlinear evolution equation is tested by Painlev′e test,its Lax pair can be obtained,that is,the equation is Lax integrable;B¨ackland transformation,multi-soliton solution,symmetry and bilinear form of the equation can be obtained by using Painlev′e standard truncated expansion of the equation.

Therefore,it is very important to find Painlev′e properties of nonlinear evolution equations.Based on this,this paper studies the Painlev′e integrability of two higher-order nonlinear equations with variable coefficients using Krusual simplification algorithm[17].

§2.Krusual simplification algorithm

Consider a given nonlinear evolution equation(group)

u=(u1,u2,...,um),ui=ui(x,t),i=1,...,m,,u(m)represents all m-order derivatives.If the equation(2.1)can pass the Painlev′e test,then

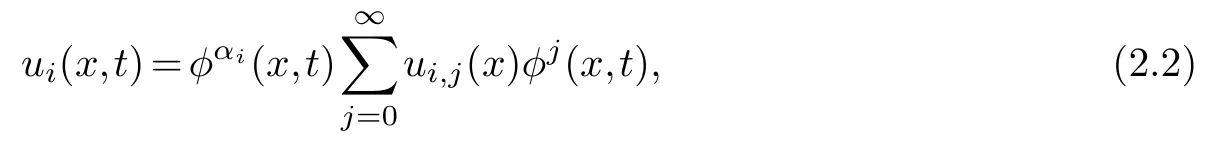
there are any functions with the same order as the equation(2.1),whereφj(x,t)=x+ψ(z).

Kruskal algorithm verifies the Painlev′e integrability of the equation,including the following three steps.

Step 1.Lead term analysis,substituting

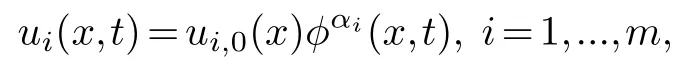
into the equation(2.1),comparing the lowest power ofφto obtainαiand.For some equations,ifαihas more than one value,each value ofαishould be analyzed in the following steps.Ifαiis not a negative integer,the algorithm is suspended.

Step 2.Determine a resonance point set.Substitutingui(x,t)=+(x,t),i=1,...,m,into the equation(2.1),collecting the lowest power ofφto obtainQ(j)+uj(x)=0,Q(j)isn×nmatrix.

is an algebraic equation ofj,the root of the algebraic equation is the set of resonance points.

If the algebraic equation(2.3)has non-integer roots,that is the equation(2.1)has algebraic branches and cannot pass Painlev′e test,the algorithm is suspended.For a single equation,if the equation(2.3)has multiple roots,that is,the equation has a logarithmic fulcrum and cannot pass the Painlev′e test,the algorithm is suspended.If the equation is a coupled equation group,there may be the same resonance point.

Usually-1 is a resonance point of the equation(2.1),which corresponds to the arbitrariness ofφ.

Step 3.Determine compatibility conditions.For the equation(2.1)to have the Painlev′e property,substituting

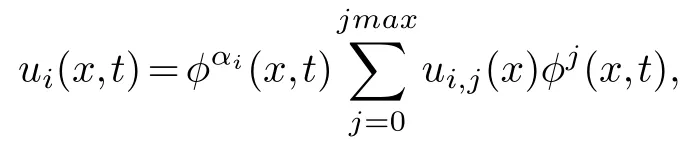
into the equation(2.1),jmax is the maximum resonance point.Comparing the power coefficients of,determine the value of the corresponding coefficient at the non-resonant point,and the obtained coefficient value is used to check whether the compatibility condition at the resonant point is established.If so,the equation(2.1)can pass the Painlev′e test,otherwise,it cannot pass the Painlev′e test.

§3.Painlev′e analysis of the higher order generalized non-autonomous equation

In actual optical fiber systems,non-uniformity of optical fiber materials is caused by processing errors,changes in fiber diameter,changes in lattice parameters and other reasons.When the non-uniformity of optical fiber needs to be considered,the nonlinear Schrodinger equation with variable coefficients is more in line with physical reality than the equation with constant coefficients[1,3,5,9,12].This section studies a high-order generalized nonautonomousequation[10].

The equation

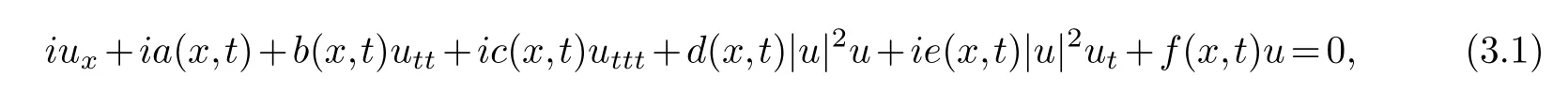
can describe the transmission of ultrashort optical pulses in nonlinear non-uniform optical fibers.tandxrespectively represent normalized time coordinates and distance coordinates.u(x,t)is the envelope of the electric field.a(x,t)is the first-order dispersion term.b(x,t)is the second-order dispersion term.c(x,t)is the third-order dispersion term.d(x,t)is nonlinear kerr effect.e(x,t)is the time delay effect.f(x,t)is a non-uniform parameter related to phase modulation and gain(loss).

The bright soliton solution and the abnormal wave solution of the equation(3.1)are studied by hirota method in Xiyang XIE[15,16],but Painlev′e of the equation has not been studied yet.Based on this,this paper mainly uses Kruskal test algorithm to study the Painlev′e property of the equation(3.1).

If the complex conjugate ofu(x,t)is denoted asv(x,t),equation(3.1)can be reduced to

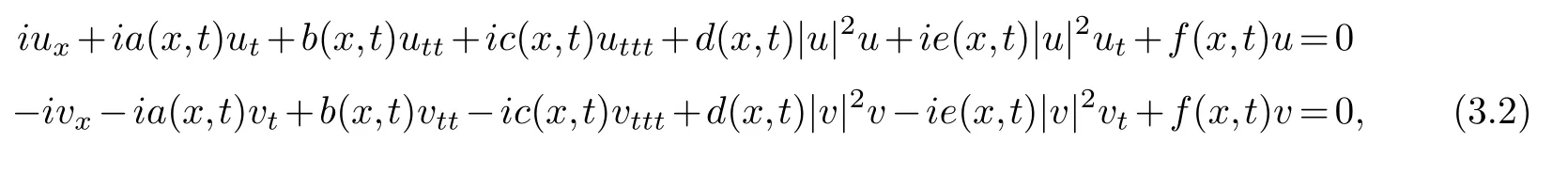
it is assumed that the solution in equation group(3.2)can be expanded into Laurent series of the following formφ

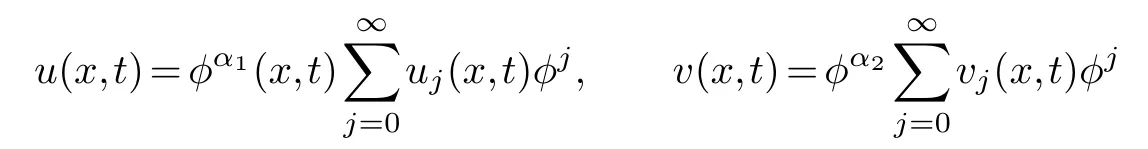
thenφ=φ(x,t)=t+ψ(x).

First of all,letu=u0(x,t)φα1,v=v0(x,t)φα2,analyze the main terms of the equations(3.2)and we can getα1=-1,α2=-1.Substitutingu=u0(x,t)φ-1,v=v0(x,t)φ-1into the equation group(3.2),collecting the same power of (φ-4,φ-4)and making its coefficient zero,we get

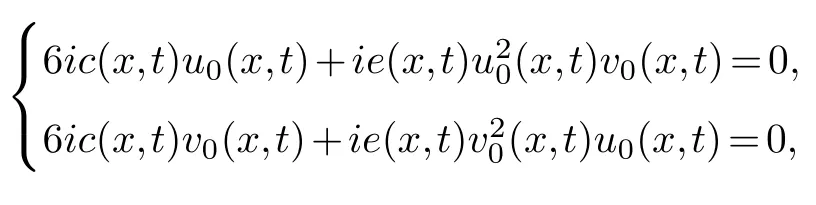
solving this system of equations is available

u0(x,t)is arbitrary.

Secondly,substituting

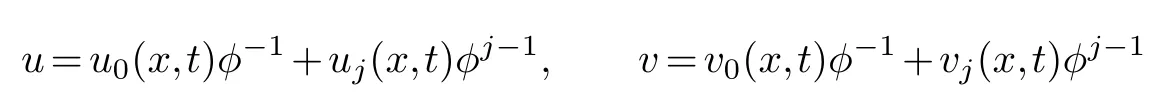
and(3.3)into the equation group(3.2),collecting the same power of (φj-4,φj-4),the following resonance point equation can be obtained-c(x,t)2j(j-1)(j-3)(j-4)(j-5)(j+1),therefore,the resonance point of equation(3.1)is 0,-1,1,3,4,5.

Finally,the compatibility condition is determined.Substituting

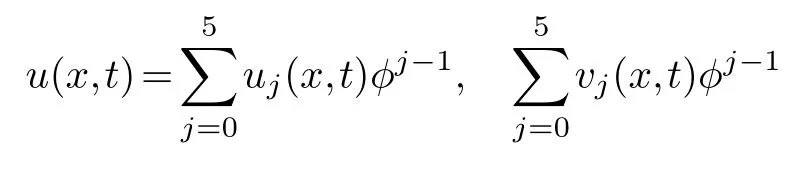
and(3.3)into the equation group(3.2),collecting the same power of (φ-3,φ-3)and making its coefficient zero,we get

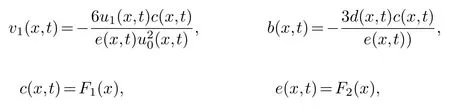
u0(x,t),u1(x,t)are arbitrary,F1(x),F2(x)are about any function ofx.

Collecting the same power of (φ-2,φ-2)and making its coefficient zero,we get

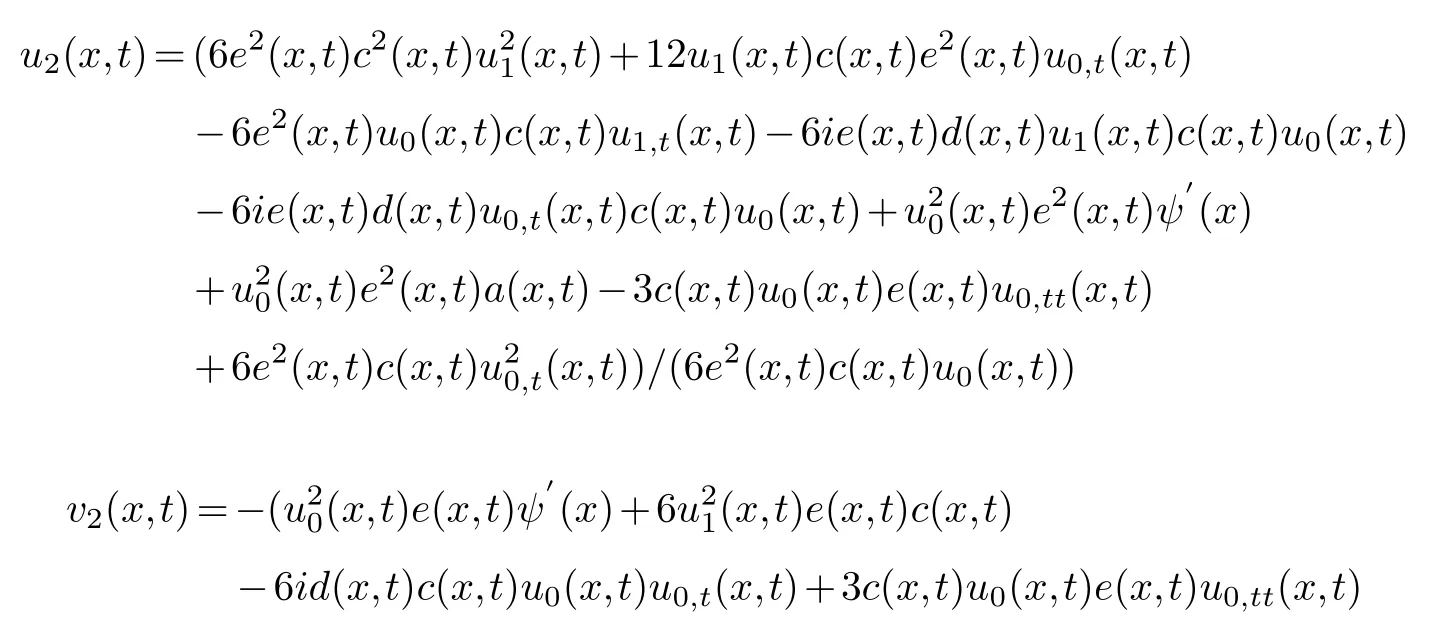
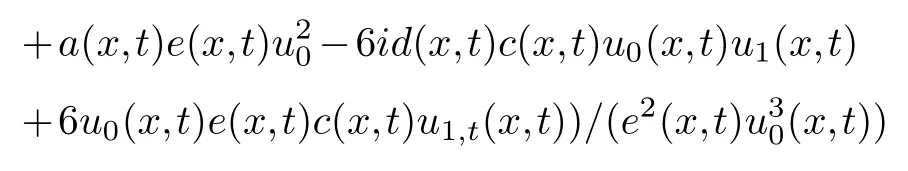
Collecting the same power of (φ-1,φ-1)and making its coefficient zero,we get

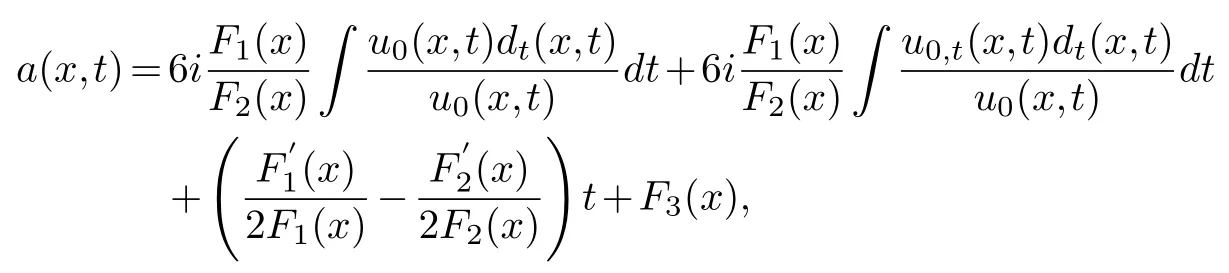
F1(x),F2(x),F3(x),are about any function ofx.One is arbitrary ofu3(x,t)andv3(x,t).

Collecting the same power of (φ0,φ0)and making its coefficient zero,we getd(x,t)=F4(x),F4(x)is about any function ofx.One is arbitrary ofu4(x,t)andv4(x,t).

Collecting the same power of (φ1,φ1)and making its coefficient zero,it can be obtained that one ofu5(x,t)andv5(x,t)is arbitrary and the compatibility condition is established on the basis of the previous conditions.

Therefore,when the parameters in equation(3.1)satisfy

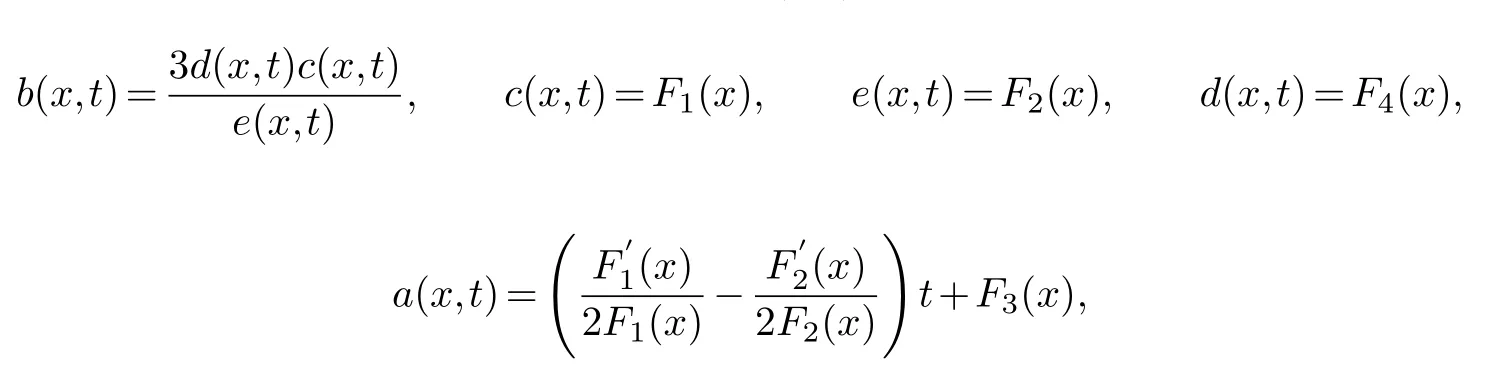
can pass the Painlev′e test,F1(x),F2(x),F3(x),F4(x)are about any function ofx.

§4.Painlev′e analysis of the third order Korteweg-de Vries equation with variable coefficients

In general,the variable coefficient nonlinear model can describe more complex nonlinear phenomena than its corresponding constant coefficient model.However,the variable coefficient model is usually not completely integrable unless the variable coefficient satisfies some restrictions[6,7,14].This section studies athird order Korteweg-de Vries equation with variable coefficients[13].

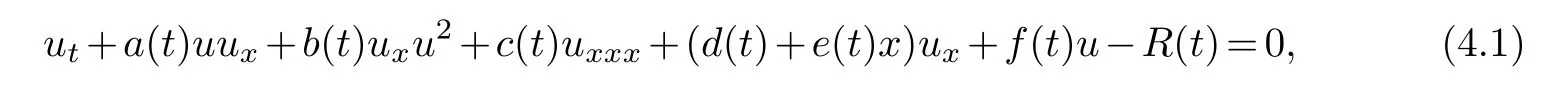
u=u(x,t)is the amplitude of the wave.xandtrespectively represent normalized spatial and temporal coordinates.Real functiona(t),b(t),c(t),d(t),e(t),f(t)represents second-order nonlinearity,cubic nonlinearity,dispersion,dissipation,non-uniformity and linear attenuation coefficient.R(t)is an external force term.Model(4.1)can describe the atmospheric blocking phenomenon.Some literatures have studied the reduced form of model(4.1).Jun Chai studied the infinite conservation law,B¨acklund transformation and soliton solution of model(4.1)[4].Based on this,this paper mainly uses Kruskal test algorithm to study the Painlev′e property of the equation(4.1).

It is assumed that the equation(4.1)can be expanded into Laurent series of the following formφ

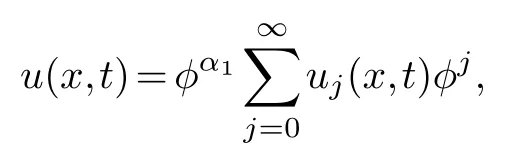
thenφ=φ(x,t)=x+ψ(t).

First of all,letu=u0(x,t)φα1,analyze the main terms of the equation(4.1)and we can getα1=-1.Substitutingu=u0(x,t)φ-1into the equation(4.1),collecting the same power of (φ-4,φ-4)and making its coefficient zero,we get

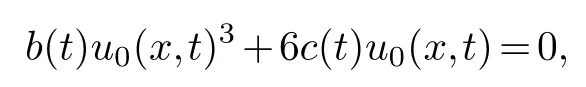
solving the equation is available

Secondly,substitutingu=u0(x,t)φ-1+uj(x,t)φj-1,and(4.2)into the equation group(4.1),collecting the same power of (φj-4,φj-4),the following resonance point equation can be obtained

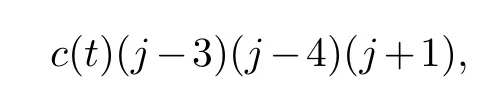
therefore,the resonance point of equation(4.1)is 0,-1,3,4.

Finally,the compatibility condition is determined.Substituting

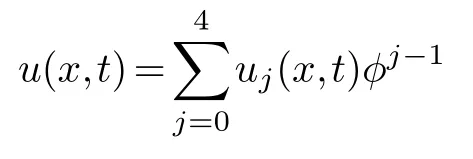
and(4.2)into the equation(4.1),collecting the same power of (φ-3,φ-3)and making its coefficient zero,we get

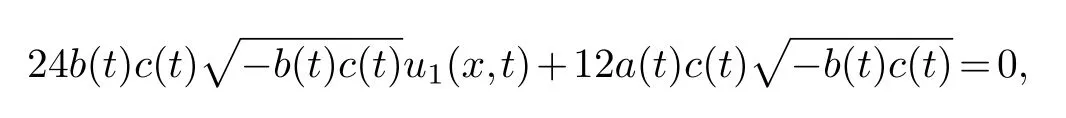
solving the equation is available

Collecting the same power of (φ-2,φ-2)and making its coefficient zero,we get

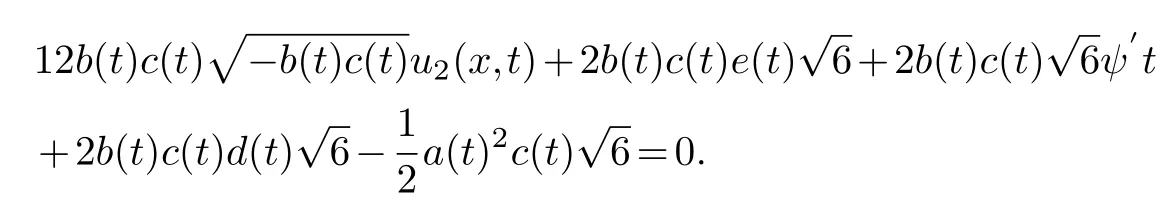
solving the equation is available

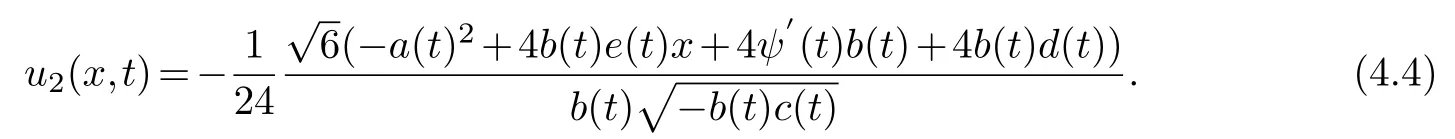
Collecting the same power of (φ-1,φ-1)and making its coefficient zero,we get

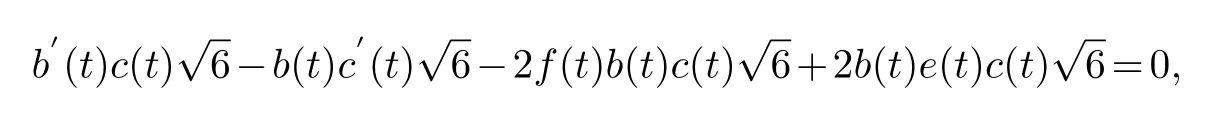
solving the equation is available

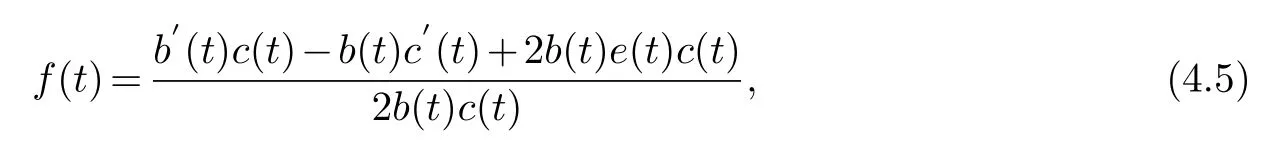
u3(x,t)are arbitrary.

Collecting the same power of (φ0,φ0)and making its coefficient zero,we get

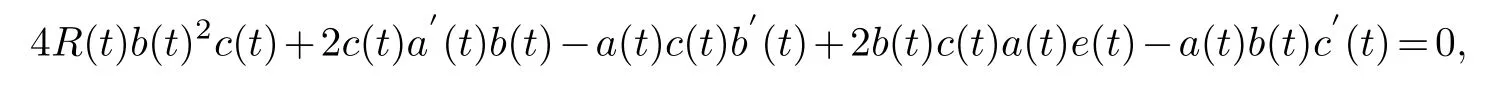
solving the equation is available

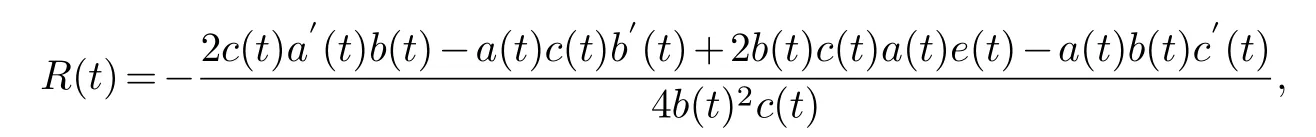
u4(x,t)are arbitrary.

Collecting the same power of (φ1,φ1)and making its coefficient zero,it can be obtained the compatibility condition is established on the basis of the previous conditions.Therefore,when the parameters in equation(4.1)satisfy

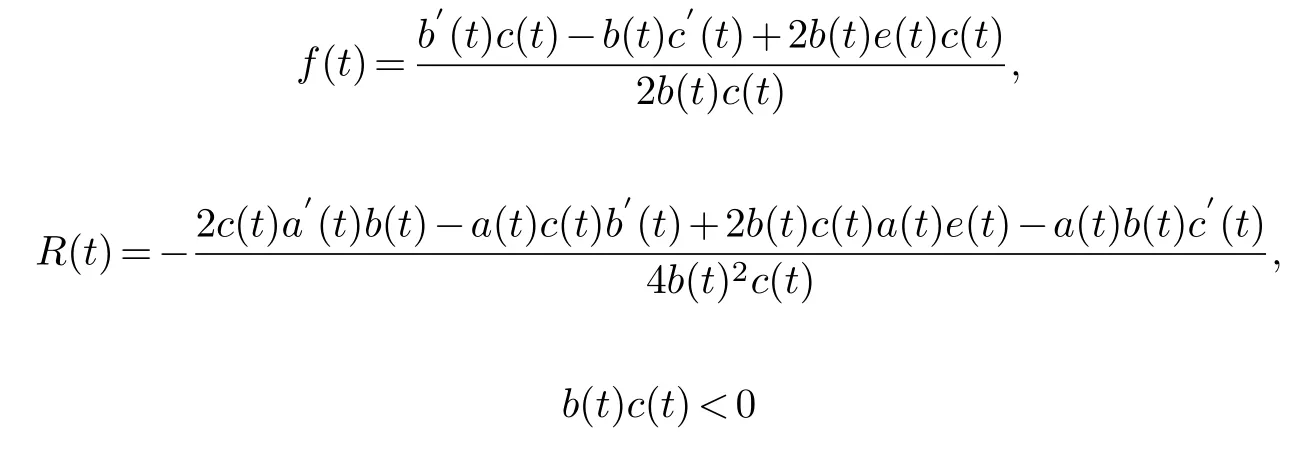
can pass the Painlev′e test.

§5.Conclusion

In this paper,by means of symbolic computation software Maple and the simplified Weiss-Tabor-Carnevale(WTC)method,Painlev′e tests are carried out for higher-order generalized nonautonomous equations and third-order variable coefficient KdV equations,and finally Painlev′e integrable conditions for these two equations are obtained.On this basis,other integrable properties such as B¨acklund transformation,symmetry,Darboux transformation,Lax pair and conservation law can be further studied by using truncated Painlev′e expansion.