王 偉, 李本伶

射影平坦spray的射影Ricci曲率

王 偉, 李本伶*

（寧波大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 浙江 寧波 315211）

研究了射影Ricci平坦的spray和度量, 首先討論射影平坦spray在給定的體積元條件下何時(shí)滿足射影Ricci曲率為0的條件. 在此基礎(chǔ)上, 刻畫(huà)出在常用的Busemann-Hausdorff體積元情形下, 射影平坦Randers度量的射影Ricci曲率, 并給出Ricci曲率為常數(shù)時(shí)該度量的具體構(gòu)造.

射影平坦; Ricci曲率; Randers度量

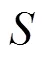
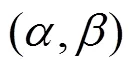
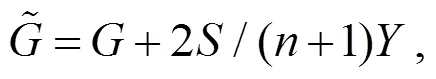
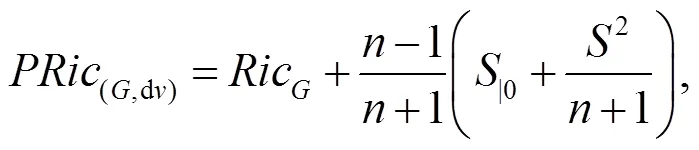
為研究射影Ricci曲率對(duì)spray和度量的影響, 首先考慮射影平坦spray的射影Ricci曲率, 得到射影Ricci曲率為0時(shí)其體積元滿足的等價(jià)條件(定理1); 其次考慮具有應(yīng)用價(jià)值的Randers度量, 得到Busemann-Hausdorff體積元(以下簡(jiǎn)稱B-H體積元)下其射影Ricci曲率, 以及射影Ricci曲率為0時(shí)其Ricci曲率的具體表達(dá)式(定理2). 研究結(jié)果給出的等價(jià)條件和刻畫(huà)的具體度量有利于發(fā)現(xiàn)新的具有應(yīng)用價(jià)值的度量及其幾何.

1 基礎(chǔ)知識(shí)及主要定理

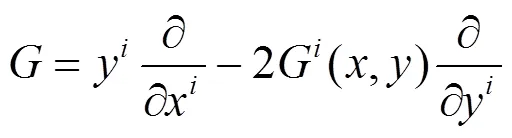
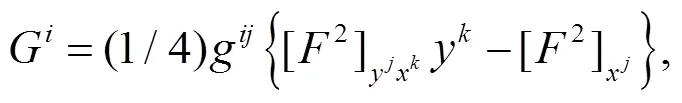
在芬斯勒幾何中, 黎曼曲率由Berwald[10]引入, 可以視作黎曼幾何中黎曼曲率的推廣. 黎曼曲率定義為:

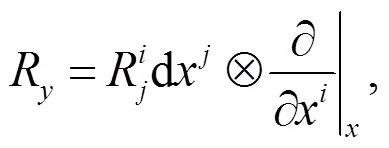
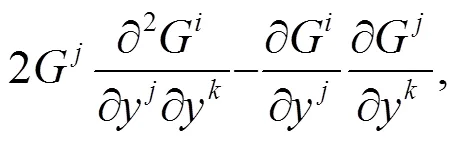
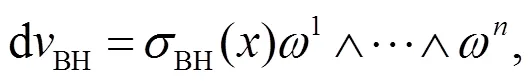
本文第3節(jié)討論的體積元都是B-H體積元.

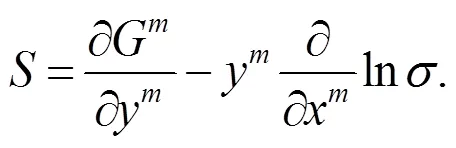
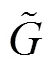
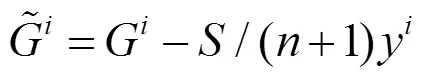
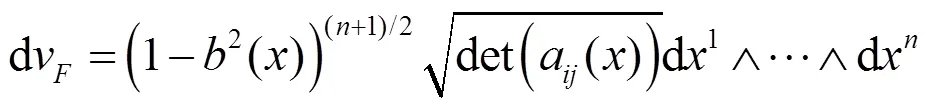
本文主要得到如下2個(gè)定理.

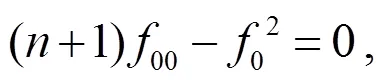
Randers度量在物理、生物等領(lǐng)域上有著重要應(yīng)用. 利用定理1, 可考慮Randers度量情形的射影Ricci曲率, 射影Ricci曲率對(duì)于研究芬斯勒幾何有著重要意義.

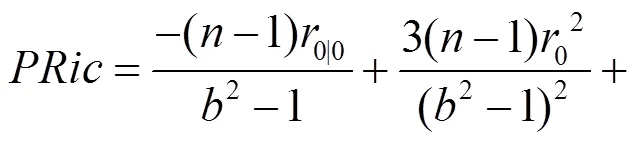
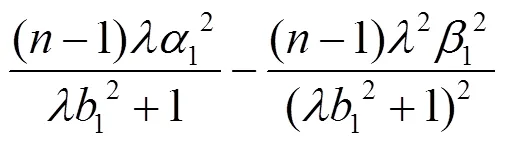
2 定理1的證明及其相關(guān)結(jié)果

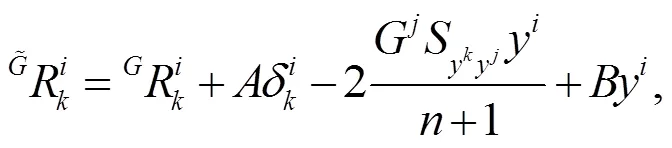
式中:

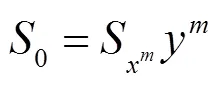
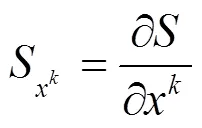
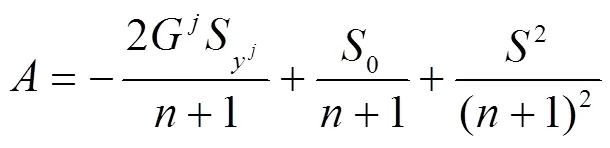
對(duì)式(2)關(guān)于和縮并, 再由Ricci曲率定義可得:

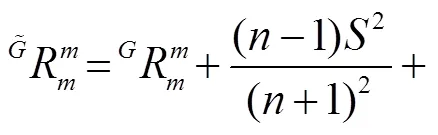
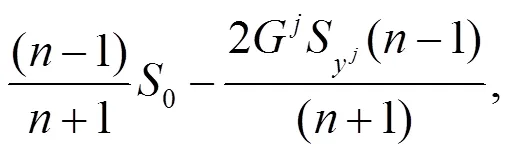
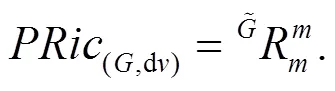
證明 當(dāng)為射影平坦時(shí),

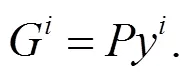
將式(5)代入式(3)可得:

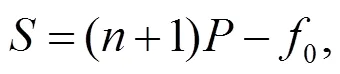
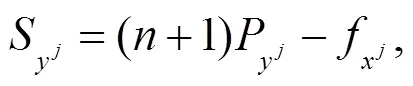
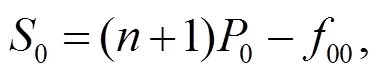
由文獻(xiàn)[5]可知:

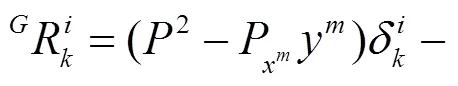
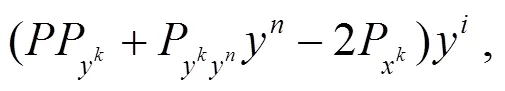
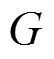
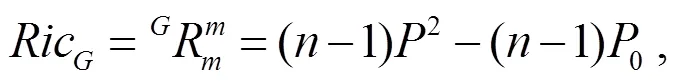
將式(5)～(8)和式(10)代入式(4), 可得:

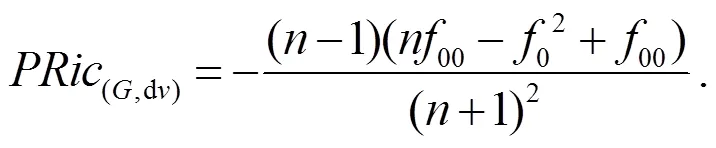
定理1的證明

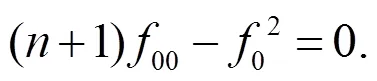
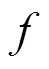
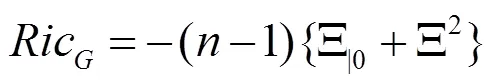
再由文獻(xiàn)[2]可得:

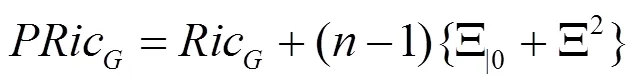
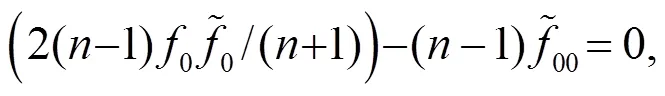
將式(11)和式(12)聯(lián)立得:

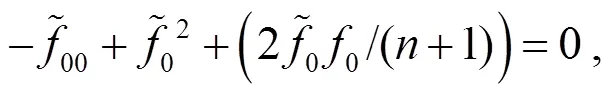
3 定理2的證明及其應(yīng)用

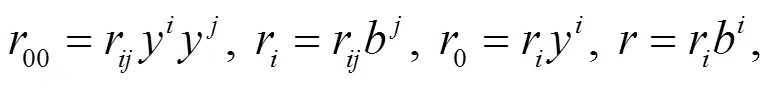
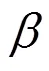
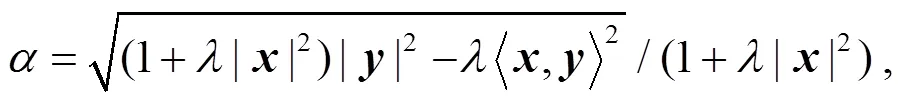
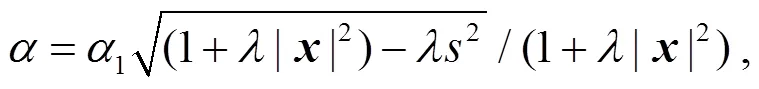
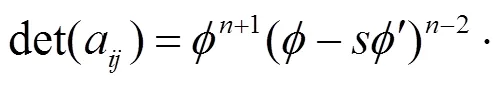
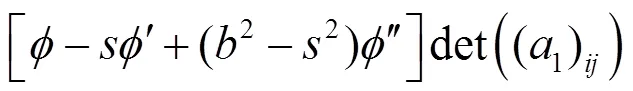
定理2的證明

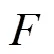
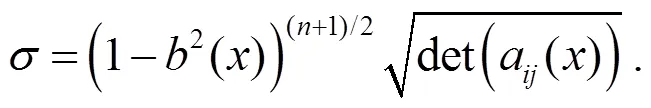
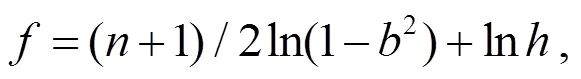
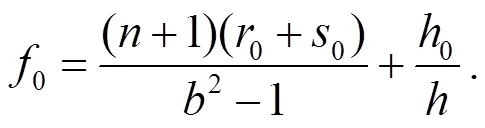
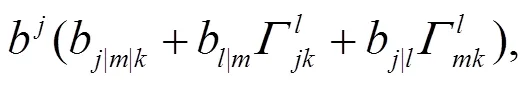
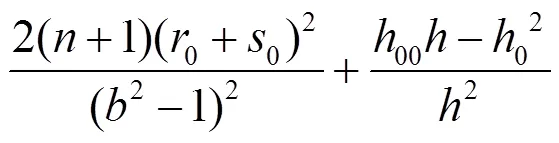
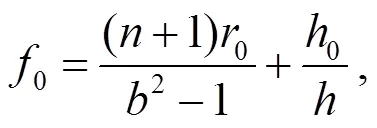
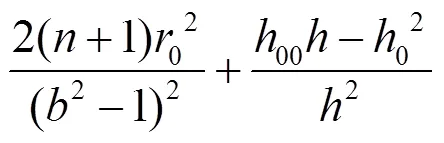
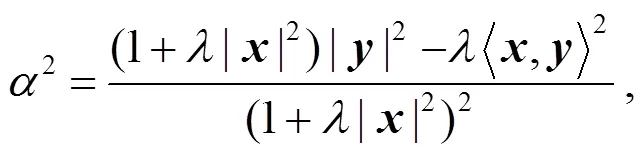
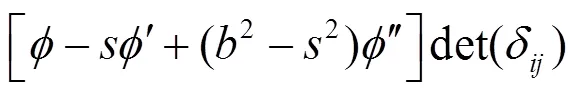
其中:

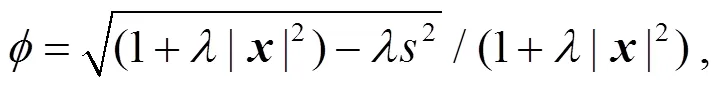
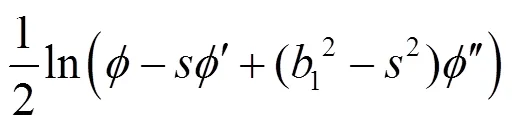
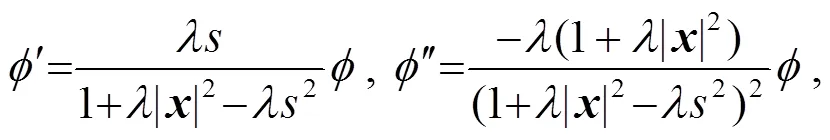
將式(23)代入式(22), 求得:

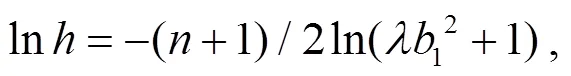
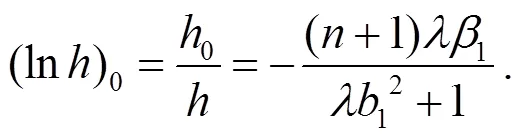
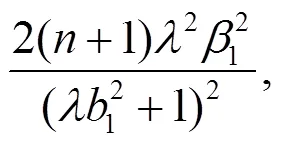
將式(24)代入式(19)可得:

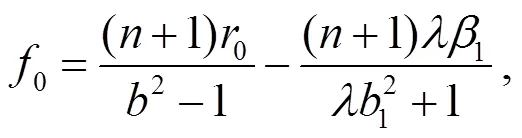
將式(25)代入式(20)可得:

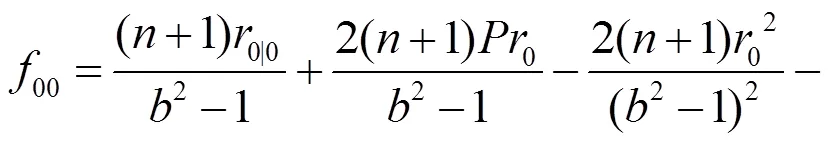
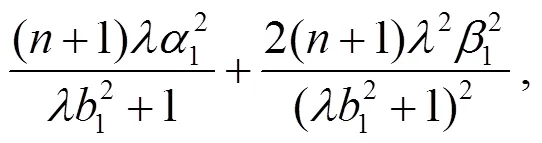
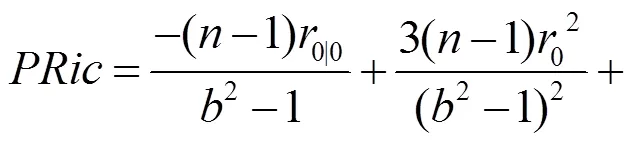
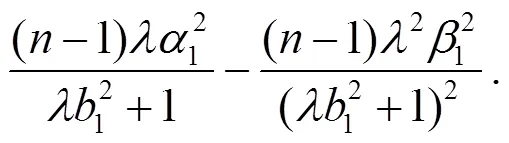
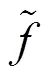
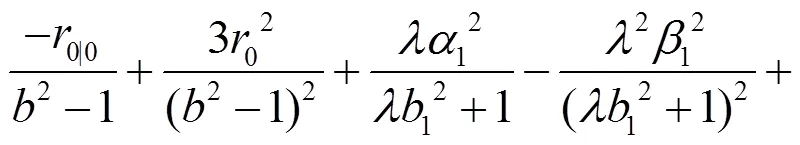
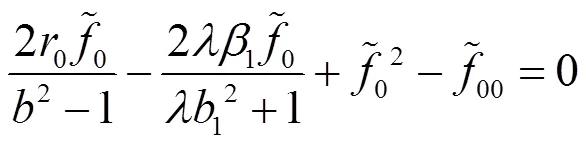
以下將研究Randers度量在B-H體積元下考慮其射影Ricci曲率為0的情形, 進(jìn)而求解該條件下度量的具體構(gòu)造. 由式(28)可得Randers度量的射影Ricci曲率為:

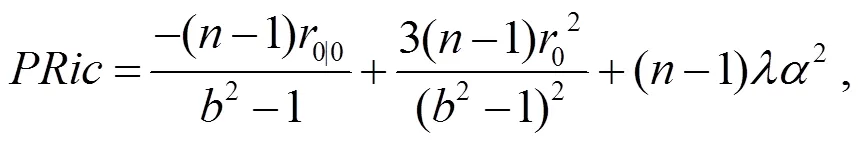
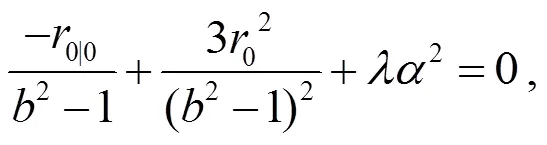
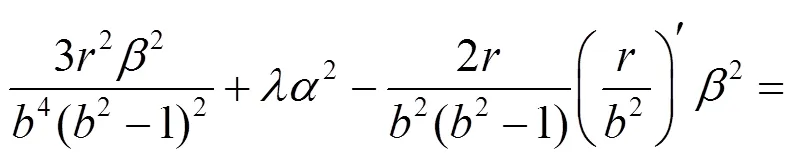
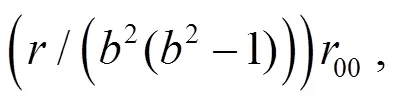
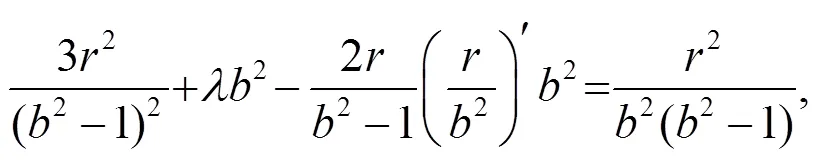
解式(31)可求得:

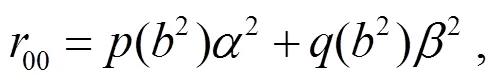
式中:

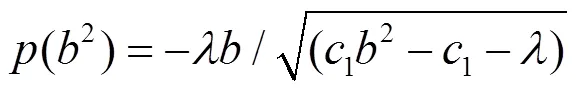
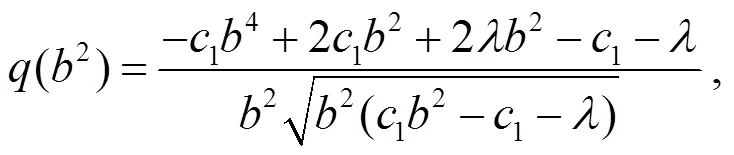
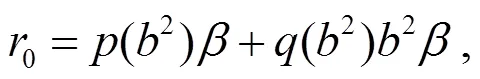
對(duì)式(32)求共變導(dǎo)數(shù)可得:

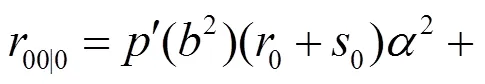
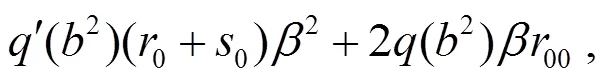
根據(jù)文獻(xiàn)[9], 當(dāng)Randers度量為射影平坦時(shí),

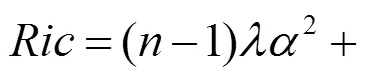
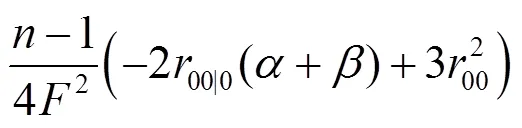
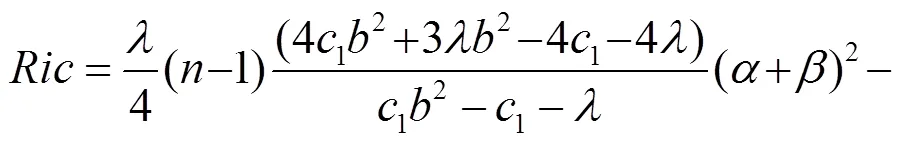
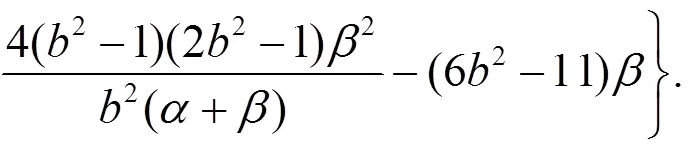
證明 將式(32)～(34)代入式(35), 可得式(36), 引理3得證.

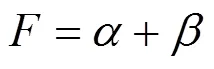
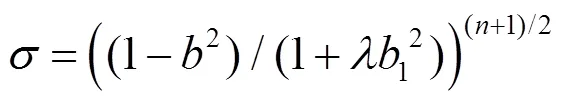
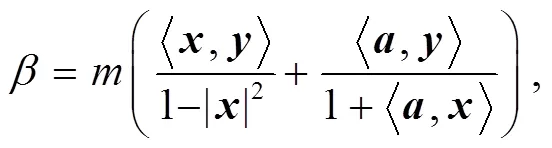
證明 在射影Ricci曲率為0的條件下, Ricci曲率由式(36)給出. 通過(guò)引理4得:

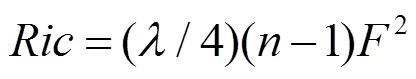
則要求如下方程成立:

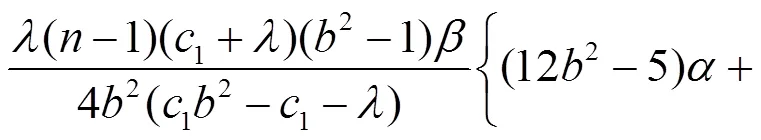
等價(jià)于

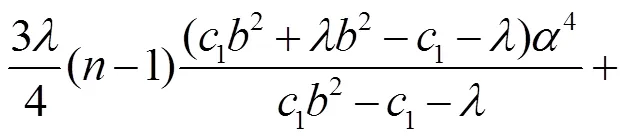
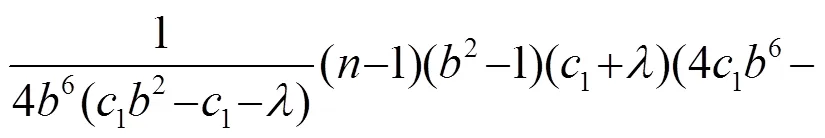
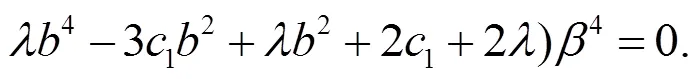
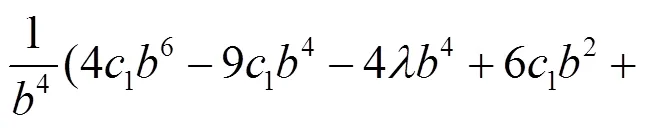
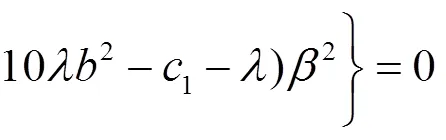
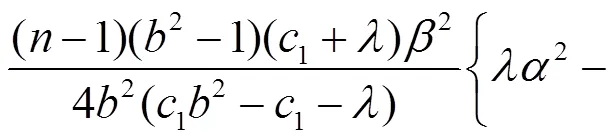
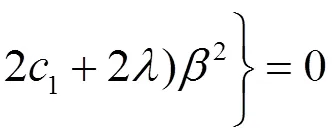
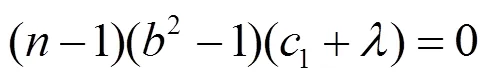
從文獻(xiàn)[8]可得:

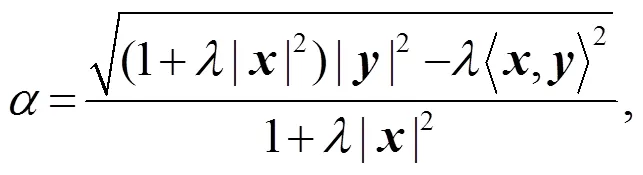
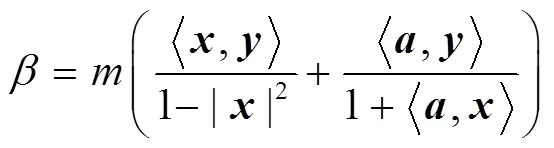
例1 射影Ricci曲率為0的Randers度量實(shí)例.

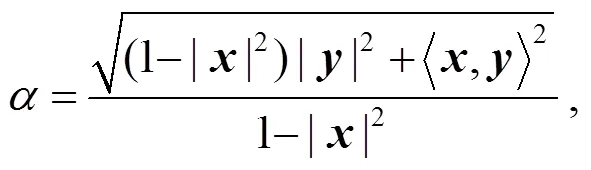
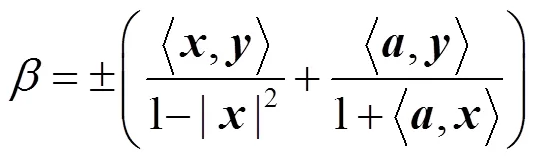
取B-H體積元下的體積函數(shù):

,

根據(jù)文獻(xiàn)[8]得:

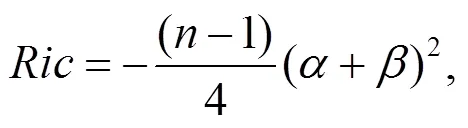
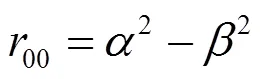
這與式(32)計(jì)算結(jié)果一致, 即此度量為射影Ricci曲率為0的愛(ài)因斯坦度量.

[1] Shen Z M. Differential Geometry of Spray and Finsler Spaces[M]. Dordrecht: Springer Netherlands, 2001.

[2] Shen Z M, Sun L L. On the projective Ricci curvature[EB/OL]. [2020-08-20]. http://doi.org/10.1007/ s11425-020-1705-x.

[3] Shen Z M. On projectively flat (,)-metrics[J]. Canadian Mathematical Bulletin, 2009, 52(1):132-144.

[4] 吳亞?wèn)|, 李本伶. 一類局部射影平坦的廣義(,)-度量[J]. 寧波大學(xué)學(xué)報(bào)(理工版), 2017, 30(1):64-67.

[5] Li B L, Shen Z M. Sprays of isotropic curvature[J]. International Journal of Mathematics, 2018, 29(1): 1850003.

[6] Yu C T, Zhu H M. On a new class of Finsler metrics[J]. Differential Geometry and Its Applications, 2011, 29(2): 244-254.

[7] Cheng X Y, Shen Y L, Ma X Y. On a class of projective Ricci flat Finsler metrics[J]. Publicationes Mathematicae Debrecen, 2017, 90(1/2):169-180.

[8] Shen Z M. Projectively flat Randers metrics with constant flag curvature[J]. Mathematische Annalen, 2003, 325(1): 19-30.

[9] Li B L, Shen Z M. On Randers metrics of quadratic Riemann curvature[J]. International Journal of Mathematics, 2009, 20(3):369-376.

[10] Berwald L. Untersuchüng der krummüng allgemeiner metrischer r?ume auf grund des in ihnen herrschenden parallelismus[J]. Mathematische Zeitschrift, 1926, 26:40- 73.

[11] 沈一兵, 沈忠民. 現(xiàn)代芬斯勒幾何初步[M]. 北京: 高等教育出版社, 2013:14-114.

Projective Ricci curvature of projective flat spray

WANG Wei, LI Benling*

( School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China )

In this paper, the projective Ricci flat spray and its metrics are studied in the most part. Firstly, we discuss the case in which the projective flat spray meets the condition that the projective Ricci curvature is 0 with the given volume element. On this basis, by using Busemann-Hausdorff volume element, the projective Ricci curvature of projective flat Randers metrics is described, and the concrete structure of such metrics is given provided that the Ricci curvature is constant.

projective flat; Ricci curvature; Randers metrics

O186

A

1001-5132（2021）04-0079-07

2020?10?14.

寧波大學(xué)學(xué)報(bào)（理工版）網(wǎng)址: http://journallg.nbu.edu.cn/

國(guó)家自然科學(xué)基金（11371209）; 浙江省自然科學(xué)基金（LR18A010002）.

王偉（1997－）, 男, 湖北黃岡人, 在讀碩士研究生, 主要研究方向: 微分幾何. E-mail: wangwei2020nbu@163.com

李本伶（1979－）, 女, 浙江寧波人, 教授, 主要研究方向: 微分幾何. E-mail: libenling@nbu.edu.cn

（責(zé)任編輯 史小麗）