正多邊形同心圓的兩個(gè)性質(zhì)的推廣
廣州市鐵一中學(xué)(510600) 何重飛
文[1]研究了正多邊形的同心圓(即圓心在正多邊形中心的圓)的兩個(gè)性質(zhì): (1)正多邊形同心圓上的任意一點(diǎn)到各頂點(diǎn)距離的平方和是定值;(2)正多邊形同心圓上任意一點(diǎn)到各邊距離的平方和是定值.
本文筆者將正多邊形的同心圓推廣到正多邊形的同心橢圓(即橢圓中心在正多邊形中心的橢圓)得到
定理1設(shè)G為正n邊形的中心,則以G為中心的橢圓上任意一點(diǎn)到正n邊形的各頂點(diǎn)的距離的平方和與該點(diǎn)到橢圓兩焦點(diǎn)距離的乘積的n倍之和為定值
如右圖所示, 點(diǎn)G為正多邊形A1A2···An和橢圓C:= 1(a >b >0)的中心, 點(diǎn)P是橢圓C上的任意一點(diǎn),如右圖以G為中心建立平面直角坐標(biāo)系,設(shè)正多邊形外接圓半徑為r,
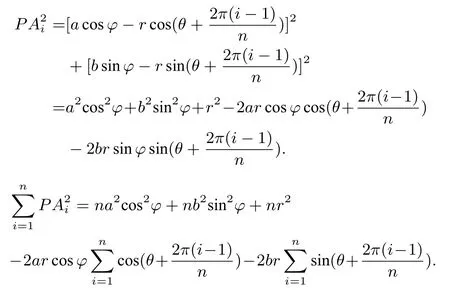
特別地,當(dāng)橢圓退化成圓,即當(dāng)a=b=PF1=PF2=r′(也即正多邊形同心圓半徑為r′)時(shí),則有如下的:
推論1[1]正n邊形的同心圓上任意一點(diǎn)到正n邊形的各頂點(diǎn)的距離的平方和為定值.
證明由定理1 知,+n·PF1·PF2=n(a2+b2+r2), 此 時(shí) 又a=b=PF1=PF2=r′, 所 以 有=n(r2+r′2).
定理2設(shè)G為正n邊形的中心,則以G為中心的橢圓上任意一點(diǎn)到正n邊形的各邊所在直線的距離的平方和與該點(diǎn)到橢圓兩焦點(diǎn)距離的乘積的倍之和為定值.
證明如定理1 中圖, 點(diǎn)G為正多邊形A1A2···An和橢圓C:= 1(a > b >0) 的中心, 點(diǎn)P是橢圓C上的任意一點(diǎn), 以G為中心建立平面直角坐標(biāo)系, 設(shè)正多邊形外接圓半徑為r, 由題意可 設(shè)Ai(rcos(θ+1,2,··· ,n),P(acosφ,bsinφ),F1(-c,0),F2(c,0)(其中c2=a2-b2), 過點(diǎn)P作正多邊形的邊AiAi+1(i= 1,2,··· ,n,且規(guī)定邊AnAn+1為AnA1) 所在直線的垂線, 垂足為Bi(i= 1,2,··· ,n), 設(shè)邊AiAi+1(i= 1,2,··· ,n) 所在直線的斜率(假設(shè)都存在)為kAiAi+1,則有
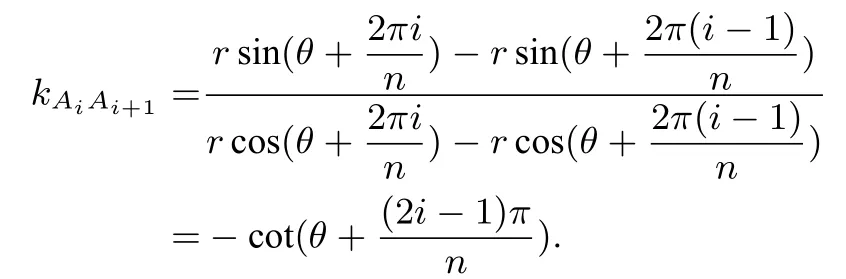
則邊AiAi+1所在直線的方程為
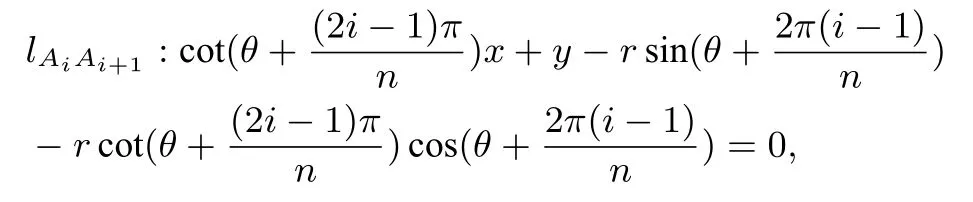
所以有
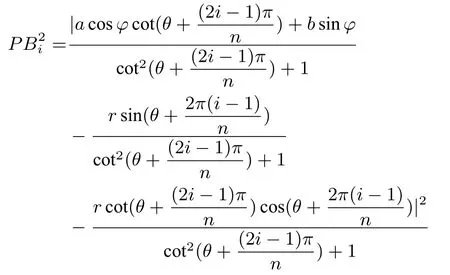

因?yàn)?/p>
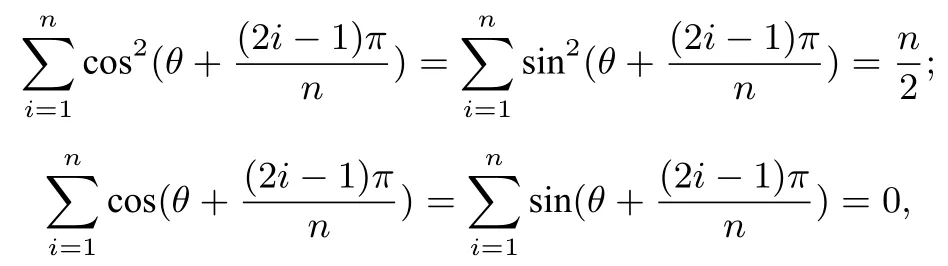
故
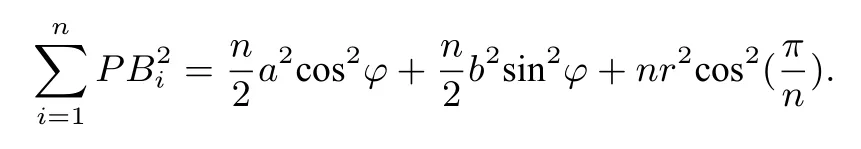
又
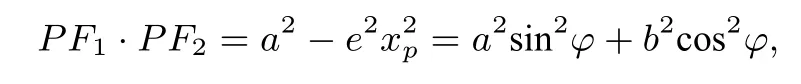
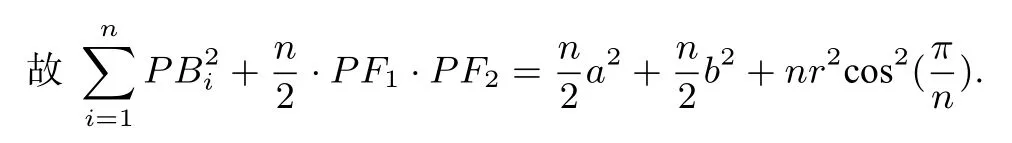
特別地,當(dāng)橢圓退化成圓,即當(dāng)a=b=PF1=PF2=r′(也即正多邊形同心圓半徑為r′)時(shí),則有
推論2[1]正n邊形的同心圓上任意一點(diǎn)到正n邊形的各邊所在直線的距離的平方和為定值
證明由定理2 知,而a=b=PF1=PF2=r′, 所以

